多性能強耦合分析技術及應用

王曉燕 郝文權 蔣永峰

（中國第一汽車股份有限公司 研發總院，長春 130013）

主題詞：多學科 強耦合 分布式 算法

1 概述

多學科交叉耦合問題在車輛性能開發過程中變得越來越突出，采用多學科分析技術是提高車輛綜合性能的必要手段[1-2]。傳統的多學科分析是一種弱耦合技術[3-4]，不同學科之間只是簡單的信息交互，沒有求解器層面的耦合，因而難以完全表達不同學科之間的相互影響關系。此外，在車輛性能集成過程中，供應商出于對自身核心技術保護的角度考慮，不會把子模型以白箱的方式完全提供給主機廠，給整車性能集成帶來困難。因此，需要探索一種強耦合算法，以實現不同學科在求解器層面的耦合，同時每個子模型僅需提供界面上的力與運動信息，實現“分而治之”的多學科強耦合分析[5]。

2 關鍵算法

如前所述，多學科強耦合分析算法只依賴于模型的接口信息，接口指的是兩個模型的連接或共同的表面。接口可以用一組有限元模型中的接口節點或者一組多體動力學模型的鉸鏈來表征。典型的接口信息分為運動信息和力信息。運動信息包括接口的位移、速度和加速度，力信息指的是接口傳遞的力與力矩。

耦合任何機械系統，力學原則要求接口處滿足兩組條件：

（1）力的大小，即接口力必須滿足作用力與反作用力的平衡方程。

（2）接口處的運動量，必須要滿足兼容條件。

如果定義好一組滿足平衡條件的接口力變量，那么在耦合過程中只需要考慮運動量的兼容性條件。在這種情況下，接口力變量可以視為接口運動量的函數，并且這些接口力變量可以利用運動信息和兼容條件進行更新迭代。類似地，如果定義好一組合適的接口運動變量，即接口運動變量滿足兼容性條件，那么在耦合過程中只需考慮接口力的平衡方程。在后者情況下，接口運動變量是接口力變量的函數，它們通過接口力的平衡條件來更新。兩種不同的方式可以衍生出不同的耦合策略。

圖1展示了T-T戰略，以兩個子系統的情況為例進行說明。在這個戰略中，兩個子系統模型的接口處的運動數量被用作耦合器的輸入。兩個模型的接口力向量和耦合器輸出，將被用于子系統模型的下一步計算。

圖2說明了X-T耦合戰略。在這個方法中，兩個模型的接口向量和被用作耦合器的輸入。向量和是耦合器的輸出（其中X代表位移，T代表力）。

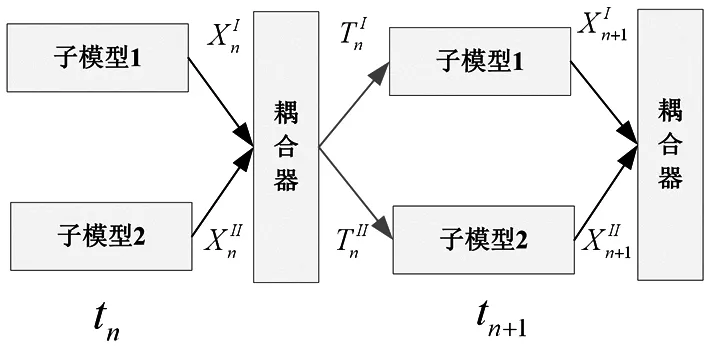
圖1 T-T方法

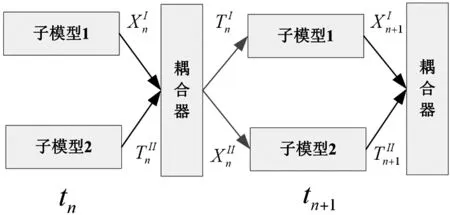
圖2 X-T方法

下面以第二種情形為例闡述粘合算法的原理。

2.1 粘合算法[6][7]

假設X是合理定義的接口運動向量，其包含了必要和足夠的變量能夠代表接口的運動向量空間；F是合理定義的接口力向量，其包含了必要和足夠的變量能夠代表接口的力向量空間。并且X-T策略中接口位移X是自平衡，即如果接口處耦合輸入信息是X，此接口自動滿足位移兼容條件。e作為一個誤差測量向量代表了接口力向量偏差，其中e=0表明接口力向量滿足平衡條件。在通常情況，e可視為校正力變量Fc的函數，即

由于采用X-T耦合策略，運動向量自動滿足兼容條件，那么粘合算法的唯一目標就是使得e等于零，即找到適當的Fc滿足

方程（2）定義了一組（線性或非線性）方程，可以通過選擇適當的算法（線性或非線性）方程求解器來解決。首先可以嘗試使用擬牛頓法BFGS[8]進行求解，定義T接口校正力變量的初值為,其中yk是梯度差，Bk是Hesse矩陣。

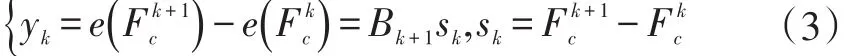
然而工程絕大多數問題都是大規模、強非線性問題，BFGS算法雖然計算速度快，但是收斂上存在一定的魯棒問題，因此需要研究更多高效穩定的迭代方法，例如LM+TrustRegion[9]方法：

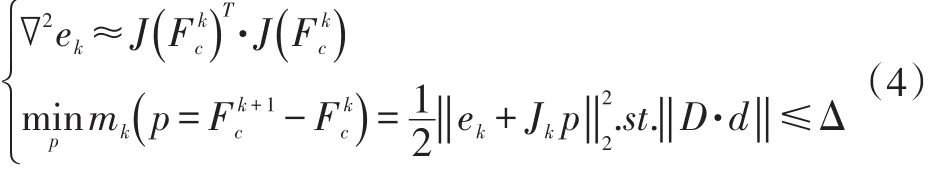
方程（3）以及方程（4）表明可以只利用接口的信息來獲得適當的校正力Fc，使得接口滿足力平衡條件。工程實踐中，隱式算法首先使用BFGS算法進行初步計算，迭代過程中發現若不容易收斂，切換至LM+TrustRegion算法計算，這樣既能保證收斂穩定性，同時又能提高計算速度。

2.2 延時預測計算方法

在多學科耦合過程中多體動力學計算與結構有限元計算存在一個時間步的延遲，迭代不易收斂或者不收斂，可采用近似模型技術進行預測解決此問題，具體算法步驟如下：

（1）對預測量的時間序列進行差分平穩化；

（2）建立時間序列分析模型；

（3）進行模型參數估計并驗證模型；

（3）還原差分進行預測。

2.3 多學科強耦合算法在商業化軟件中的實現

如前所述，多學科強耦合算法需要各子模型邊界上的力與運動信息，在實際問題中，各子模型都是在各自的分析軟件中求解，因此如何將多學科強耦合算法嵌入至商業化軟件中，是首要解決的問題。比較理想的情況是直接針對商業化軟件的內存進行操作來讀取相應模型的信息，但這樣涉及到各商業化軟件的底層操作，需要商業化軟件開放底層信息，實現起來工作量較大。本文在研究過程中，利用分析軟件提供的程序外部接口，將每個子模型的仿真控制信息及計算結果進行存儲，然后利用程序重新啟動的命令來實現不同軟件的信息傳遞及耦合。圖3顯示了ADAMS與ABAQUS聯合分析的程序流程，在每一仿真步，ADAMS與ABAQUS分別對相應的子模型進行求解，并將子模型的仿真控制參數及結果信息保存至文本中。Mega-Solver粘合算法從結果文件中讀取相應的邊界運動信息，判斷是否滿足容差條件，如果滿足，則進行下一步求解；如不滿足，則根據迭代算法計算新的邊界載荷向量，同時更新模型文件中相應的載荷信息，退回到當前步仿真起始點，調用當前步存儲的模型控制參數文件，利用重啟動命令重新進行當前步的分析。

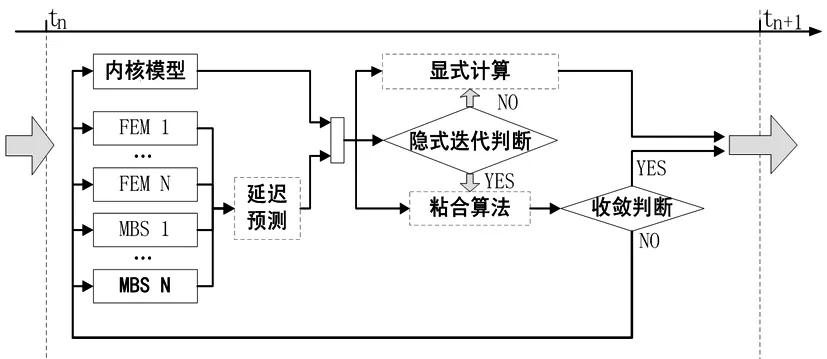
圖3 ADAMS與ABAQUS強耦合分析流程

3 多學科強耦合分布式分析技術[10][11]

多學科強耦合算法“分而治之”的建模思想，使得分布式建模的技術手段變得比較容易實現[12][13]，因為Mega-Solver粘合算法只需要子模型的邊界信息，不需要模型的詳細內部結構，因此可以在不同的客戶機上仿真不同子模型的特性，將子模型的分析結構通過數據傳輸的方式傳遞給主機，在主機上運行多學科強耦合Mega-Solver的主程序，通過粘合算法將各子模型的邊界信息進行耦合，再將粘合算法的計算結果傳遞給各子模型進行迭代求解，從而完成整個系統的耦合分析。

本文在研究過程中，建立了基于OPC技術的分布式仿真平臺，如圖4所示。基于多體與有限元耦合技術，利用MATLAB語言為主控機編寫了控制代碼，通過OPC服務器技術可以實現對客戶機分配任務及傳遞客戶機的計算結果；為客戶機編寫了計算控制代碼，可以接受或等待主機分配計算任務并接受主機傳遞的計算結果數據，根據計算需要可以連接多臺客戶機。

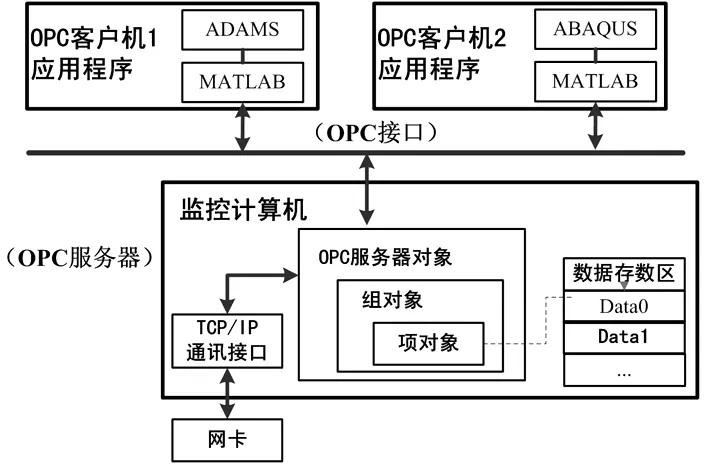
圖4 基于OPC的多學科強耦合分布式分析技術

4 多學科強耦合分析案例

4.1 多體動力學耦合分析

根據前述多學科強耦合算法原理，考慮多體動力學耦合分析案例。如圖5所示，在ADAMS中，將一根桿的一端用襯套固定在大地上，另一端加正弦激勵。將桿從中間一分為二，邊界節點用物體局部Marker表示，擁有6個自由度；節點之間的相互作用力通過廣義力作用在物體I和物體II上。兩個子模型分別在AD?AMS中進行求解，利用耦合算法進行耦合求解。

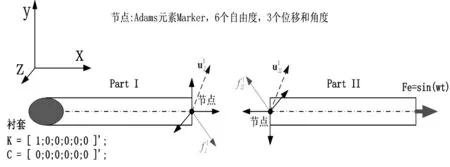
圖5 多體動力學強耦合分析案例

圖6 為耦合求解結果與ADAMS整體求解結果的對比，從圖中可以看出，耦合算法較精確地模擬了整體系統的運動。

4.2 多體動力學與有限元聯合分析

為驗證Mega-Solver算法的分析精度，采用簡易的鋼板彈簧結構，其兩端的鏈接方式如圖7所示，在梁的中間施加載荷。傳統的ADAMSFlex在分析過程中，采用模態疊加的方法，因此在大變形、非線性區時模型的誤差較大，通過多學科強耦合聯合分析技術，可以直接耦合ADAMS的動力學分析模型與板簧的有限元模型，因而分析精度大幅提升，圖8為采用Mega-Solver耦合算法、ADAMSFlex及有限元算法的精度對比，可以看出，采用耦合算法后，分析結構與有限元的分析精度基本吻合，而ADAMSFlex在大變形時與有限元的計算結果偏差較大。

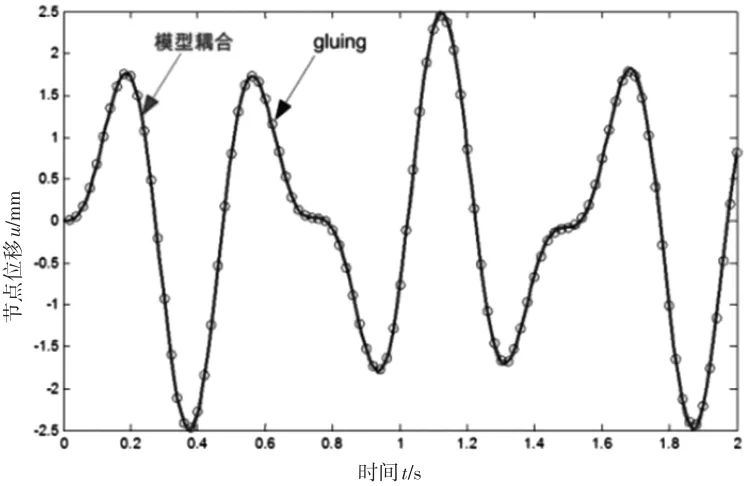
圖6 多體動力學耦合案例仿真結果

圖7 多體動力學與有限元耦合分析案例

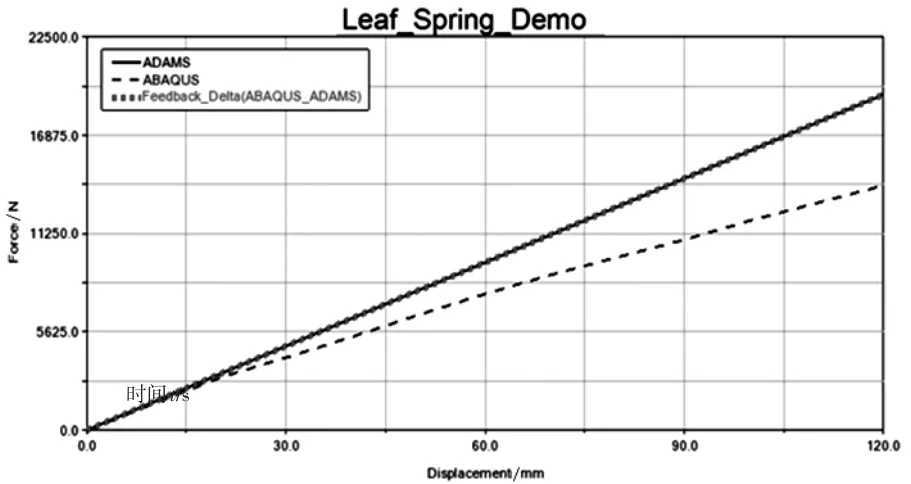
圖8 多體動力學與有限元耦合結果

4.3 整車耦合分析

利用多學科強耦合分析技術實現了整車的耦合分析建模，其中底盤系統利用動力學軟件求解，如圖9所示，車身在有限元中進行求解，如圖10所示。每一計算步，底盤與車身在連接點處進行力與運動信息的交換，通過粘合算法進行綜合求解。

5 結論

利用多學科強耦合Mega-Solver算法，可以實現多學科、多軟件的強耦合分析。Mega-Solver算法只需要界面的力與運動信息，而不必關注各子模型的內部詳細結構，從而可以進行分層模塊化的建模及分析工作。由于模型的模塊化處理，可以通過分布式技術實現子模型的同步求解，大大提高了分析的效率；同時，由于Mega-Solver本質上實現了求解器之間的耦合分析，可以充分發揮不同求解器的優勢，在處理強非線性、接觸等問題時可以進一步提升分析精度。

圖9 耦合分析底盤子模型

目前，Mega-Solver粘合算法的穩定性仍有待進一步研究，通過引入多種迭代方法相結合以及多步法等技術手段，提高算法的魯棒性。