熱軋帶鋼卷取溫度對卷后應力影響研究

聞成才 李一心 朱劍濤 孔寧 張立元

(1:馬鞍山鋼鐵股份有限公司 安徽馬鞍山 243003；2:北京科技大學機械工程學院 北京 100083)

1 前言

熱軋生產線生產帶鋼經粗軋、精軋、層流冷卻及卷取等工藝環節后成為帶鋼卷，而后以鋼卷的形式在自然環境下從卷取溫度冷卻至室溫。在卷取后自然冷卻的過程中，伴隨著溫度的變化，帶鋼發生收縮變形，引起鋼卷層與層之間相互作用的改變，帶鋼內部的應力場也將發生變化。帶鋼的降溫幅值與其卷取溫度直接相關，卷取溫度的波動會引起帶鋼卷后內部應力場和層間相互作用力的波動。卷取溫度波動量過大，會引起鋼卷產生層間縫隙甚至是層間錯動，使得鋼卷發生松卷、錯層等不良現象。

卷取溫度變化可使熱軋帶鋼再結晶晶粒直徑、析出物的量和形態發生變化，從而使其力學性能發生變化。文獻[1]介紹了帶材卷徑計算中最常用的速度計算法和圈數計算法,分析了熱軋卷取特點，比較分析了兩種方法的優缺點。陳建強[2]針對人工檢測熱軋鋼帶表面缺陷錯漏率高的現狀,提出基于深度學習的熱軋鋼帶表面缺陷檢測方法。孫鐵軍[3]、賈春玉[4]和謝海波[5]等人提出了一種將遺傳算法與神經網絡結合起來，能夠提高卷取溫度預報精度的系統。李興田[6]和李廣林[7]對實際生產中影響熱軋帶鋼寬度精度因素進行了分析，根據實踐經驗和分析，給出了提高熱軋帶鋼寬度控制精度進而提高成材率的解決方案。為探索提升熱軋帶鋼卷型的提升策略，高秀郁[8]和軒康樂[9]和左遠鴻[10]從加強卷取設備的管理與維護、加強對側導板的控制以及有效控制卷取張力等方面論述了具體的解決對策。卞皓[11]發現馬氏體相變產生的內應力超過了帶鋼的抗拉強度是導致65Mn帶鋼表面開裂的主要原因。于千[12]和郭德福[13]結合現場實際溫控數據，分別考察不同終軋溫度、卷取溫度、冷卻溫度模式下對帶鋼力學性能的影響，證明了終軋溫度升高帶鋼的屈服強度降低。此外，帶鋼厚度對帶鋼卷后應力也有較為明顯的影響[14-18]。熊文濤[14]，張清東[16]和李廣林[17]等人研究了熱軋、冷軋主要工藝參數對硅鋼橫向厚度差的影響，并優化相關工藝參數。楊光輝[19]等人基于軋制理論中體積不變原理，考慮來料板形的影響，推導出以帶鋼寬展系數和比例凸度系數表示的帶鋼平坦度模型。

本文重點關注熱軋帶鋼卷取溫度波動對其卷后應力演化的影響，具體研究內容為：首先，基于平衡方程、協調條件和本構關系，建立了熱軋帶鋼卷后自然冷卻過程的熱致變形場理論模型；接著，通過對理論模型進行數值求解，系統研究了典型溫度波動形式的幅值和發生區域，對比不同厚度規格帶鋼的卷后應力演化的影響規律；最后，根據模擬所得的應力演化規律，提出了緩解熱軋鋼卷松卷的工藝對策。本文研究為改善熱軋鋼卷卷取質量，消除松卷和層錯等不良現象具有理論參考價值。

2 熱軋鋼卷冷卻變形的理論模型

為簡化模型的影響因素并聚焦于鋼卷應力場的演化規律，本文引入如下基本假設：鋼卷為多層同心圓柱體(圖1)，卷取溫度在各層鋼卷內相同，卷取溫度波動用層間溫差表示，忽略相變帶來的影響。本模型重點關注鋼卷降溫過程中的力和變形的相對變化，將鋼卷完成卷取時的狀態作為初始狀態并設置為零應力狀態，將模型的各層從內向外依次編號為第1～n層。需要注意的，本模型中假設鋼卷為彼此相對獨立的一圈圈同心圓環，降低了層與層之間長度方向的連續性，強化了各層的變形和應力，在后續的模型分析中需要進行等效弱化處理，以使仿真結果與實際情況更為接近，更好為熱軋帶鋼的生產提供理論參考。

將鋼卷考慮為一個由n層同心圓環構成的二維結構，如圖1所示。對于第i層鋼卷，平衡條件可表示為：

σih=(pi-1,i-pi,i+1)ri

(1)

式中：pi-1,i為第i-1層鋼卷對第i層鋼卷的層間作用力，pi,i+1為第i層鋼卷對第i+1層鋼卷的層間作用力，特別的，對第1層和n層分別設置p0,1和pn,n+1=0；σi為第i層鋼卷的應力；h為帶鋼厚度；ri為第i層鋼卷的半徑(降溫變形后)。

考慮溫降之前未冷卻時的初始狀態，各層鋼卷對應的半徑之間滿足關系式：

Ri=R1+(i-1)h

(2)

式中：Ri為第i層鋼卷的半徑，R1為第1層鋼卷的半徑(降溫變形前)。

考慮溫降至室溫后自然冷卻結束時的終止狀態，各層鋼卷對應的半徑之間滿足關系式：

圖1 熱軋硅鋼凸度與成品硅鋼橫向厚度差相關性理論模型

ri=r1+(i-1)h

(3)

式中：r1為第1層鋼卷的半徑。

本構關系定義了鋼卷的應力與應變之間的關系：

σi=Eiεi=Ei(εi總-εi熱)

(4)

式中：σi為第i層鋼卷的應力；Ei為第i層鋼卷的彈性模量；εi為第i層鋼卷的彈性應變，其為該層總應變εi總與熱致應變εi熱之差。

各層鋼卷的應變由相應層鋼卷的半徑變化來定義，由此可得總應變的計算表達式為：

(5)

而熱致應變的計算表達式為：

(6)

式中：ri′為第i層鋼卷降溫后僅考慮降溫作用但不考慮變形協調時的半徑，其值只與熱膨脹系數和降溫幅值相關，表達式為：

(7)

式中：αi為第i層鋼卷的熱膨脹系數；Ti為第i層鋼卷的降溫幅值。

將式(5)和式(6)代入式(4)可得總應變與各層鋼卷半徑變化之間的關系式，即：

(8)

本模型中假設鋼卷為同心圓環，為此需要對未考慮變形協調的熱致變形進行一定的修正，具體過程如下。首先考慮相鄰的第i層和第i+1層的熱致變形之差，即鋼卷降溫后僅考慮降溫作用但不考慮變形協調時的半徑之差，由式(7)可得該關系式為：

ri+1′-ri′=h-αhTi+1+αRi(Ti-Ti+1)

(9)

式中：設定α=αi+1=αi。結果表達式中等號右側的第1項等于降溫前初始狀態時的半徑之差Ri+1-Ri=h，在變形后考慮協調變形時不引起應力；第2項-αhTi+1，將使熱致變形后的半徑之差減小，導致內外層之間趨于靠緊，內層應力減小、外層應力增加；第3項αRi(Ti-Ti+1)，其作用與內外層降溫幅值之差有關。

考慮一種理想狀態，即內外層溫度相等，此時式(9)變為ri+1′-ri′=h-αhTi+1，內外層之間的半徑之差將與降溫幅值成正比，且降溫幅值越大，半徑之差越大，內層應力減小的幅度和外層應力增加的幅度也將越大，這與實際情況存在差異。該差異一定程度上是由于理論模型中未考慮各層鋼卷在長度方向上的首尾相連所致。為了減弱該差異，在式(9)中引入溫降幅值系數，對溫降幅值導致的變形量進行修正，即：

ri+1′-ri′=h-αhλi+1+αRi(Ti-Ti+1)

(10)

式中：λi+1為第i+1層的溫降幅值系數，其值小于1。

因此，對各層鋼卷降溫后僅考慮降溫作用但不考慮變形協調時的半徑計算式(7)進行修正，表達式為：

r1′=R1(1-αT1)

r1′=ri-1′+h-αhλiTi+αRi-1(Ti-1-Ti)(i=2,…,n)

(11)

鋼卷第1層直徑與卷取機的卷筒直徑基本相同，取值為610mm。卷取溫度存在縱向波動量，各層均降溫至室溫30℃，本模型以第1層溫度為基準值580℃，其降溫幅值T1=550℃。帶鋼的基本參數包括：彈性模量E=1.8×105MPa，熱膨脹系數α=1.4×10-5/℃，厚度h=4、6、8mm，總層數85(此時厚度6mm的帶鋼總長約300m)。熱致變形修正時所用溫降幅值系數λ的取值為：λ1=…=λ10=0,

λ23=…=λ65=0.2，

λ76=…=λ85=0，以此保證鋼卷各層均勻降溫550℃時，其內部應力變化幅值在卷取應力20MPa以內，與實際情況基本相符。

3 卷取問題徑向分布模式與仿真工況

依據某鋼廠的帶鋼卷取溫度在長度方向的波動變化規律，將帶鋼卷取溫度在鋼卷中波動形式概括為3類徑向分布模式：帶頭段存在L型溫差，局部若干層存在V型溫差和局部若干層存在反Z型溫差，如圖2所示，并以此為基礎設計仿真工況。

結合上述3種卷取溫度波動形式及其分布區域，并考慮3種厚度規格的帶鋼，設計如下6組共24個工況，如表1所示，系統研究帶鋼卷后應力的演化規律。

圖2 典型溫度波動的鋼卷徑向分布模式

表1 工況匯總表

4 卷取溫度波動對鋼卷應力演化規律的影響

4.1 卷取溫度不同徑向分布模式

本小節主要討論相同帶鋼厚度(6mm)，卷取溫度不同徑向分布模式(工況1-3)對鋼卷應力演化規律的影響。

(1)帶頭段存在L型溫降

利用式(1-11)計算工況1A-1C的結果，提取層內應力分布如圖3a-3c所示，應力最小值如圖3d所示。從圖3可以看出：隨著層與層之間降溫幅值的增加，層內應力圖上在鋼卷產生L型波動層數范圍內會產生一條折線，在產生波動層數內側層內應力逐漸增大，外側層內應力逐漸減小，且線性溫降層數越大，折線斜率越大。從圖3d中可知，在帶鋼帶頭產生L型波動的層數Δn不同，鋼卷冷卻后層內應力的變化不同，層內應力隨著溫降幅值的增加，從先壓后拉變為先拉后壓，此外，隨著產生L型波動的層數Δn越大，層內應力產生L型波動的最小值越小，且層內應力最小值與降溫幅值線性負相關。

(2)局部若干層存在V型溫差

工況2A-2F的仿真結果顯示隨著層與層之間降溫幅值的增加即ΔT=0,10,20,30,40,50℃，層內應力在產生V型波動層數附近逐漸減小，其他層數均為增大。鋼卷產生V型波動的位置不同，鋼卷冷卻后產生的層內應力不同。提取仿真結果的應力最小值與總降溫幅值關系，如圖4所示。圖4(b)可知,當層數Δn越大時，層內應力的最小值也隨層數的增多而變大。

圖3 鋼卷前卷區域存在L型分布溫差的層內應力(MPa)：(a)工況1A，(b)工況1B，(c)工況1C，(d)不同降溫層數的層內應力最小值與總降溫幅值關系曲線

(3)局部若干層存在反Z型溫差

工況3A-3F的仿真結果表明隨著層與層之間降溫幅值的增加，層內應力圖上會在相應層數上產生反Z型曲線，在產生反Z型層數范圍內層內應力先逐漸減小后增大，在其他區域內呈逐漸增加趨勢。提取仿真結果的應力最小值與總降溫幅值關系，如圖5所示。從圖5(a)來看，產生波動的位置越靠后，層內應力的最小值越小，當鋼卷產生反Z型波動的位置在內圈附近時，對鋼卷冷卻后產生的影響更大。從圖5(b)可知，當層數Δn越大時，鋼卷的層內應力變化幅度越大，層內應力圖上的Z型寬度隨差值也隨之增大。層內應力的最小值與降溫幅值呈線性負相關，且層數Δn越大，層內應力最小值與降溫幅值的斜率越小。

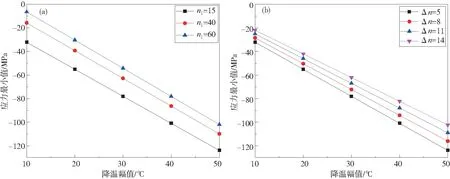
圖4 層內應力最小值與總降溫幅值關系：(a) V型波動發生在Δn=5時，不同位置隨降溫總幅值的變化曲線，(b) V型波動發生在n1=15時，不同層數隨降溫總幅值的變化曲線

圖5 層內應力最小值與總降溫幅值關系：(a)反Z型波動發生在Δn=4時，不同位置隨降溫總幅值的變化曲線,(b)反Z型波動發生在n1=15時，不同層數隨降溫總幅值的變化曲線

4.2 不同厚度帶鋼

從4.1節分析結果可知，當卷取溫度在帶鋼長度局部區域內存在L型(單調降低)的波動時，對鋼卷自然冷卻過程的影響最大。而卷取溫度在帶鋼長度局部區域內存在V型或反Z型的波動時，波動位置位于帶頭段(n1=15)時，對鋼卷自然冷卻過程的影響更為明顯。因此本小節選用工況4-6中的參數設置，討論相同卷取溫度徑向分布模式，鋼卷的規格參數對鋼卷自然冷卻過程的影響，依次選擇帶鋼厚度h=4,6,8mm。各工況應力趨勢與4.1節相同，因此本小節主要討論不同工況下帶鋼的厚度對層內應力最小值的影響，計算結果如圖6所示。從圖6可以看出：帶鋼厚度的改變對帶鋼內產生L型溫降的影響最大，對V型和反Z型波動的幾乎沒有影響。此外，可以看到隨著帶鋼厚度的增加，鋼卷內層內應力逐漸減小。

基于上述結果可知：對于卷取溫度的3類波動模式，相同規格的帶鋼產生L型溫降波動對應的層內應力最小值最小，其次是V型溫差波動和反Z型溫差波動。對于不同規格的帶鋼，本節關注了卷取溫度的L型、V型和反Z型溫降波動的影響，結果表明，對于L型溫降波動，帶鋼厚度越厚，產生的層內應力最小值越小；而對于V型和反Z型溫降波動，帶鋼的厚度對帶鋼的層內應力變化幾乎沒有影響。

5 結論

熱軋帶鋼卷取溫度存在較大的波動，且波動形式多樣，經過對多組實測卷取溫度進行歸納分析，將帶鋼卷取溫度的波動中的不利變化情形概括為3類主要型式。首先，建立了熱軋鋼卷下機自然冷卻過程的熱致變形模型，根據實測卷取溫度的3類波動型式，設計了帶鋼卷取溫度在鋼卷中的3類徑向分布模式及相應的仿真工況，系統研究了熱軋帶鋼卷取溫度波動對卷后應力演化規律的影響，具體結論為：

(1)熱軋帶鋼卷取后的應力變化主要受卷取溫度波動的影響，其中溫度波動的位置n1越靠前、產生溫降的層數Δn越少和溫差幅值ΔT越大，鋼卷層內應力降低幅值越顯著。

(2)相同規格的帶鋼，發生L型溫降波動對應的層內應力降低幅值最顯著，其次是V型溫差波動和反Z型溫差波動。

(3)不同規格的帶鋼，發生L型溫降波動時，帶鋼厚度越厚，產生層內應力的降低幅值越大，而對于V型和反Z型溫降波動，帶鋼厚度對其層內應力變化幾乎沒有影響。