信道突變對正交調制傳輸性能影響的分析方法

劉建成，郝學坤，王賽宇，王 超，姜少飛

(1. 中國電子科技集團公司第五十四研究所，河北 石家莊 050081；2.中國電子科技集團公司第五十研究所，上海 200331；3. 解放軍31634部隊，云南 昆明 611731)

0 引言

無線通信是信息時代實現全時全區域消息傳輸必不可少的通信方式，其傳輸信道包括空中無線電磁波傳輸通道和收發信機前端射頻有線傳輸通道，而自然環境和射頻器件不確定性對信息的有效、可靠傳輸造成了嚴重影響。其中，以衛星通信、深空探測等最為突出，比如電離層閃爍[1]、太陽黑子[2]和核爆[3]等均會引起空中傳輸信道的突變，而前端射頻器件的非理想特性也會引起信號的非線性畸變[4-5]。

針對信道畸變失真問題，學者們近些年開展了大量深入的研究，主要集中于射頻非線性預失真處理和空中傳輸信道特性分析等。文獻[4]首先是分析了射頻前端非線性，建立對應的數學模型，進而分析了其對大規模MIMO系統上行傳輸鏈路傳輸速率的影響。文獻[5]針對5G的大規模MIMO系統發射終端，研究了其射頻前端非線性特性及對該系統的影響，以消除射頻前端非線性產生的干擾。文獻[6]研究了發送端功率放大器非線性的數字預失真補償方法，預失真以時延線構成的網絡結構為基礎，使得發送信號較好地抑制了非線性。文獻[7]基于瑞利衰落信道，分析了功放非線性消除對MIMO MC-CDMA系統的影響。文獻[8]以衛星通信為對象，研究了除功放非線性失真外的傳輸信道幅頻特性和群延遲特性，并進行了基本仿真，為衛星通信傳輸信道分析提供了參考。文獻[9—10]研究了CDMA系統受傳輸信道非線性失真的影響，利用非線性器件的AM-AM和AM-PM特性預測發送信號的鄰道功率抑制比(ACPR)、噪聲功率比和二階交調乘積，為提升CDMA發送信號特性奠定了基礎。文獻[11]針對OFDMA上行鏈路的FBMC/OQAM傳輸信號，從接收端角度出發，分析了強頻率選擇性和定時誤差情況下的非線性失真問題，給出了子載波數目足夠大時的脈沖非線性表達式。文獻[12]針對發送端功率放大器非線性補償消除問題，分析了發送端預失真、接收端均衡和碼間串擾消除等技術方法，表明判斷反饋均衡與非遞歸結構均衡相比并無明顯提升。除此之外，文獻[13]研究了信號畸變對衛星導航測距的影響，利用大口徑天線接收、高性能濾波和多周期偽碼平均等措施恢復發送信號，指出導航信號畸變將帶來較大的測距誤差。

由上述分析可知，有效分析傳輸信道不確定性、外界環境和射頻器件等突變易對衛星通信鏈路產生的嚴重影響，是提升系統應對能力的前提基礎。針對該問題，本文提出了信道突變對正交調制信號傳輸性能影響的分析方法，提供了有力的理論和仿真數據支撐。

1 信道突變下正交調制信號數學描述

數字通信因其傳輸速率與糾錯能力可控，成為目前衛星通信的主要方式，而正交調制又是數字通信中采用最多的0、1比特映射形式，其中以QPSK和QAM應用最為廣泛，二者具有實現簡單、抗噪性能強等優勢，但其信號非恒包絡，通過無線和射頻通道時易產生非線性失真，對信道突變較為敏感。以π/4QPSK調制和矩形16QAM為例，信號矢量表示分別如圖1(a)和(b)所示，其中矢量s表示無失真的調制信號矢量，矢量s′表示突變后對應的信號矢量。對于QPSK調制，只有信號矢量的角度承載了傳輸的信息，而對于16QAM調制，幅度和角度共同承載了傳輸的信息。

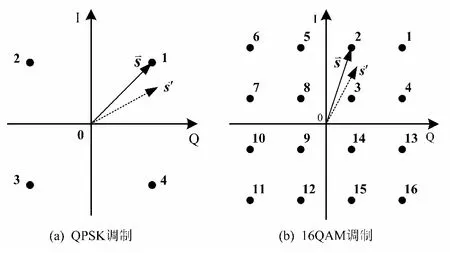
圖1 正交調制信號矢量示意圖Fig.1 Vector diagram of quadrature modulation signal

信道突變時可導致信號矢量發生由s至s′的變化，由此我們可進一步將信道異常時刻的信號畸變等價于其幅度陡降、相位突變和頻偏突變。對于QPSK和QAM等正交調制信號，其基帶信號的復數形式可表示為：s(n)=I(n)+jQ(n)，其中I(n)為同相分量，Q(n)為正交分量，j表示復數算子(j2=-1)。不妨設s(n)的強度歸一化，即正交調制信號矢量s幅度的均值為1。假設異常突變所導致的幅度陡降為β(無陡降時β=1，β越小表示陡降越嚴重)，相位突變為φ，頻偏差異為fΔ，則異常時刻的QPSK和16QAM調制基帶信號s′(n)均可表示為：

s′(n)=β·s(n)ej(2πfΔnTs+θ+φ)

(1)

式(1)中，Ts表示調制信號的符號周期，θ表示頻偏差異的初始相位，為便于分析，可令：

φ′=θ+φ

(2)

在式(2)基礎上，則s′(n)可進一步表示為：

s′(n)=I′(n)+jQ′(n)=βI(n)cos (2πfΔnTs+φ′)-
βQ(n)sin (2πfΔnTs+φ′)+
j[βQ(n)cos (2πfΔnTs+φ′)+
βI(n)sin (2πfΔnTs+φ′)]

(3)

由式(3)可見，在信道突變時，正交調制信號的I和Q路均會產生明顯失真，且與三個變化參量均有關系。

2 分析方法

信道突變造成的信號失真如何影響信號質量和系統傳輸性能是我們最關注的，為此本節提出基于信號EVM和系統誤碼率Pe的分析方法，研究信號三個變化參量與二者之間的關系，并推導數學閉合表達式，為后續分析提供有力的理論支撐。由于QPSK和16QAM應用較為廣泛且具有代表性，故本節仍以二者為例進行分析，其具體方法和推導過程可適用于其他正交調制方式。

2.1 突變對EVM影響的分析

根據式(3)可計算，QPSK和16QAM調制信號s(n)與s′(n)之間差異為：

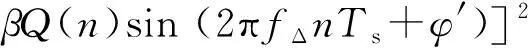
(4)

令：

θn=2πfΔnTs+φ′

(5)

進一步整理可得：

e(n)=I2(n)+Q2(n)+
β2[I(n)cos (θn)-Q(n)sin (θn)]2+
β2[Q(n)cos (θn)+I(n)sin (θn)]2-
2I(n)β[I(n)cos (θn)-Q(n)sin (θn)]-
2Q(n)β[Q(n)cos (θn)+I(n)sin (θn)]

(6)

e(n)=I2(n)+Q2(n)+
[I2(n)+Q2(n)]β2[cos2(θn)+sin2(θn)]-
2β2I(n)cos (θn)Q(n)sin (θn)+
2β2I(n)cos (θn)Q(n)sin (θn)-
2βI2(n)cos (θn)+2βI(n)Q(n)sin (θn)-
2βQ2(n)cos (θn)-2βI(n)Q(n)sin (θn)

(7)

e(n)=I2(n)+Q2(n)+
β2[I2(n)+Q2(n)]·[cos2(θn)+sin2(θn)]-
2βcos (θn)[I2(n)+Q2(n)]=
[I2(n)+Q2(n)][1-2βcos (θn)+β2]

(8)

由式(8)可得異常突變時刻的QPSK和16QAM信號EVM表達式如下：

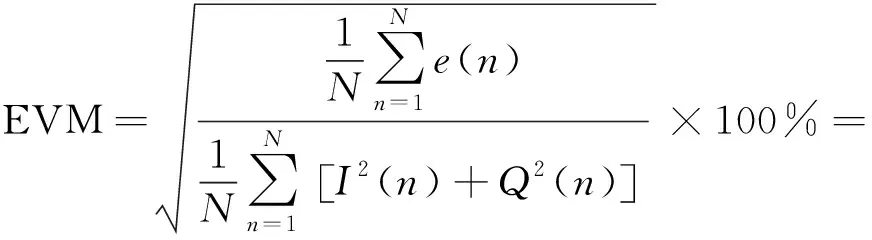
(9)

在信號強度歸一化情況下，對于QPSK信號有I2(n)+Q2(n)=1，將式(2)和式(5)代入式(9)，可得突變時刻幅度陡降為β，相位突變為φ，頻偏差異為fΔ與QPSK信號EVM之間的數學閉合關系式，如式(10)所示：

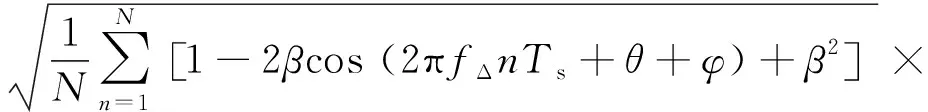
(10)

對于16QAM調制，當信號強度歸一化時，I2(n)+Q2(n)取值為1/5、1和9/5三種情況，且三種取值出現概率分別為0.25、0.5和0.25。所以，當符號個數N足夠大時，可得16QAM信號EVM與幅度陡降β，相位突變φ和頻偏差異為fΔ之間的數學閉合關系式：

(11)

分析式(10)和式(11)可見，QPSK和16QAM調制信號EVM值具有相同表達式，與幅度陡降、相位突變以及頻偏差異都息息相關，若信號無陡降即β=1，相位無突變φ=0，頻偏差異fΔ為0，則理論計算的EVM值為0，與實際相符。當信號存在突變時，隨著陡降的加劇EVM值會隨之增大，當陡降一定時EVM值也會隨著相位突變和頻率偏移的變化而增大。

2.2 突變對系統誤碼率Pe影響的分析

除信號EVM值之外，系統誤碼率也是反映突變影響的另一個重要指標。為便于分析，假設QPSK和16QAM信號畸變未發生在同步符號傳輸的時刻，并不影響系統同步定時性能。

對于QPSK和16QAM調制，無突變時系統接收基帶信號r(n)均可表示為：

r(n)=s(n)+ε(n)=
I(n)+jQ(n)+εi(n)+jεq(n)

(12)

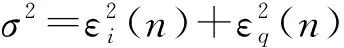
(13)

式(13)中，Es表示符號能量，n0表示符號周期對應的噪聲強度，該式中大小等于σ2。

由于突變引起的幅度陡降、相位突變和頻偏差異具有隨機性，在系統接收端表現出信息符號采樣值的無規律變化，近似于接收符號上疊加了系統噪聲，所以分析系統誤碼率變化的核心是推導信號突變對信噪比的惡化。參考突變信號表達式(3)，突變后的接收信號表示為：

r′(n)=s′(n)+ε(n)

(14)

此時接收信號的信噪比等價計算為：

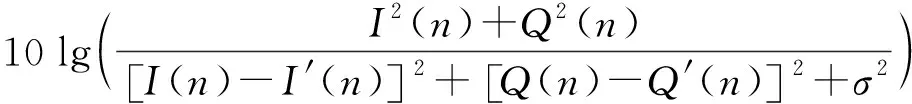
(15)

進一步推導，可得：

(16)

(17)

利用式(5)化簡可得：

(18)

所以，由信號瞬時突變引起的系統接收端信噪比惡化可由信噪比差值體現，表達式為：

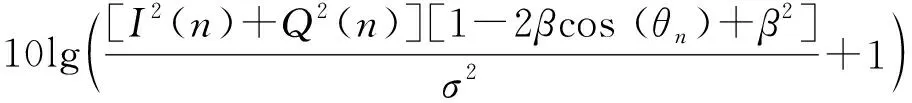
(19)

在式(18)基礎上可得突變情況下，將信噪比數值由dB轉換為比值，可得QPSK調制系統接收端誤碼率公式表示如下：

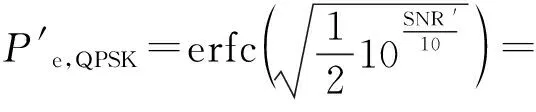
(20)

式(20)中，I2(n)+Q2(n)為原信號強度，通常情況下可將其歸一化，則系統誤碼率變為：

(21)

同理，將信道突變后16QAM信號的信噪比代入其誤碼率表達式，具體可參考文獻[14]，即可求得信道突變時所對應的系統誤碼率。

可見，幅度陡降越嚴重，即越β取值越小，相位突變量θn越大，則誤碼率將越大，所以幅度陡降和相位變化共同決定了信道突變對系統誤碼率的惡化程度。另外，式(19)所示的有無瞬時變化所對應的接收端信噪比差值也可反映出系統性能，即差值越大表示系統性能惡化越嚴重，對應的是幅度陡降、相位突變和頻偏差異的增加。

3 實驗仿真

在上述理論推導基礎上，通過實驗和仿真進一步分析信道畸變對正交調制傳輸的影響。利用課題組現有的衛星通信收發終端和儀器，搭建如圖2所示的衛星通信正交調制傳輸鏈路實驗環境。利用外圍電路實驗環境中的功率放大器，模擬傳輸信道的突變。以QPSK信號為例，通過矢量分析儀在突變前后觀測的信號EVM和星座圖如圖3所示。

圖2 信道突變測試環境Fig.2 Channel break test environment

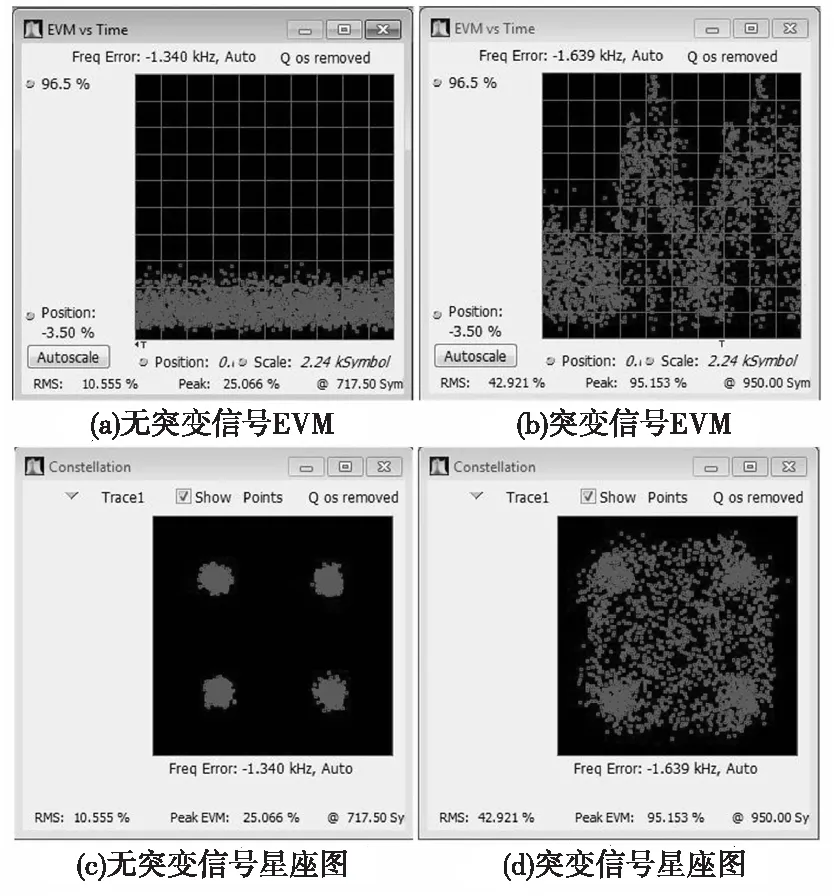
圖3 突變前后信號EVM和星座圖對比Fig.3 Comparison of signal EVM and constellation before and after channel break

由圖3所示測試結果可知，QPSK信號EVM測量值在信道突變前由于噪聲影響約為25%，而伴隨信道突變其大小突然猛增，高達95%以上；QPSK信號星座圖突變前雖然因噪聲影響略有擴散，但仍相對集中于四個象限，而當傳輸信道發生突變時，星座圖發生嚴重的彌散，隨機分布在四個象限，已無法區分判決。可見，當無線通道或者射頻通道發生突變，QPSK信號的EVM和星座圖將發生顯著的失真，進而惡化了其傳輸性能。

為進一步量化分析信道突變對正交調制傳輸性能影響，建立仿真模型，通過蒙特卡洛仿真統計不同突變情況下對應的系統誤碼率。由式(5)和2.2節分析可知突變產生的頻率差異與相位變化可相互轉換，故仿真設置不同的陡降比η和相位突變為φ兩個變量，統計分析信道突變對QPSK和16QAM調制EVM與系統誤碼率的影響，其中幅度陡降比η由β計算得出，關系為η=(1-β)×100%。同時引入突變出現周期Tp和持續時間td兩個參數，信道突變周期表示在時間Tp內隨機出現一次信道突變，持續時間為td。仿真環境設置基于以QPSK和16QAM調制為主的衛星通信傳輸鏈路，其傳輸信道多徑效應較弱，通常可近似為白噪聲信道，設定的信道突變條件下鏈路參數如表1所示。

表1 QPSK、矩形16QAM調制的鏈路仿真參數Tab.1 Simulation parameters of QPSK and 16QAM

為分析信道突變對信號EVM值的影響，設定傳輸信道比特信噪比Eb/N0為12 dB，無信道突變對應的接收端信號EVM值為25.01%，對于不同的幅度陡降比和相位突變對應的信號EVM仿真和理論計算值如表2所示。對比由式(10)和式(11)計算的理論值和統計平均的仿真值可見，仿真結果與理論分析相吻合，對比分析不同參數所對應的信號EVM仿真和理論值變化，進而可知信道突變對鏈路傳輸性能的惡化程度。

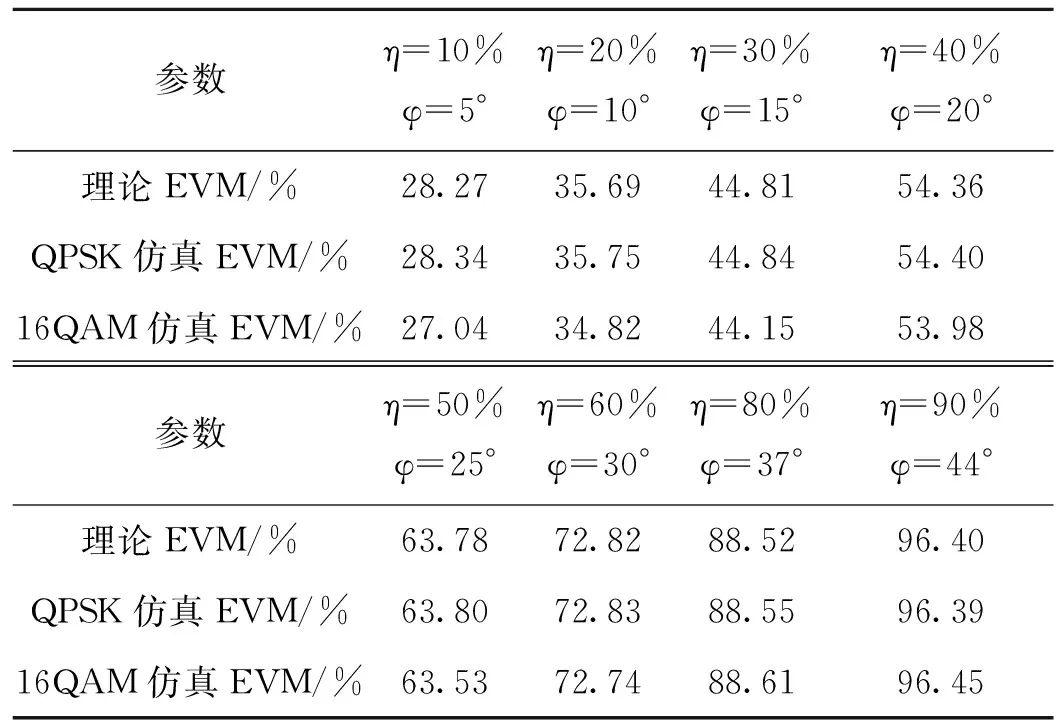
表2 信道突變對應的信號EVM值Tab.2 Signal EVM value corresponding to channel break

為直觀反映信道突變對鏈路傳輸性能的影響，設定QPSK和16QAM調制鏈路比特信噪比分別為6 dB和9 dB，單位時間內有多次信道突變，每次持續時間相同，具體參數設置同表1。統計平均1 000次蒙特卡洛仿真結果，QPSK和16QAM調制鏈路對應的誤碼率變化分別如圖4和圖5所示。

由圖4和圖5所示的信道突變情況下鏈路傳輸誤碼率結果可見，信道突變將會嚴重惡化QPSK和16QAM鏈路的傳輸性能。以仿真條件中設定的信道突變條件為例，當幅度陡降比為30%，相位突變為10°，由圖4(a)和圖5(a)可知QPSK和16QAM傳輸鏈路誤碼率均約為10-5，此時鏈路傳輸可靠性還能滿足大部分應用；而當幅度陡降比增加至50%，相位突變為20°時，QPSK鏈路傳輸誤碼率惡化約為0.004，16QAM鏈路傳輸誤碼率約為0.008，已無法保證信息的可靠傳輸。另外，分析圖4(a)和圖5(a)誤碼率曲線變化趨勢，表明無論信道突變是否導致相位突變，只要幅度陡降超過30%則會嚴重惡化QPSK和16QAM鏈路傳輸性能，分析圖4(b)和圖5(b)可知對于相位突變大于20°時，即使幅度陡降比較小也會造成QPSK和16QAM鏈路傳輸性能的嚴重惡化。

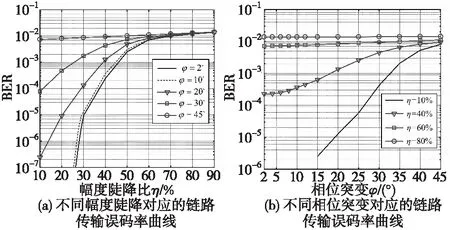
圖4 QPSK調制鏈路受信道突變影響的誤碼率變化曲線Fig.4 Variation curve of BER of QPSK modulation link affected by channel break

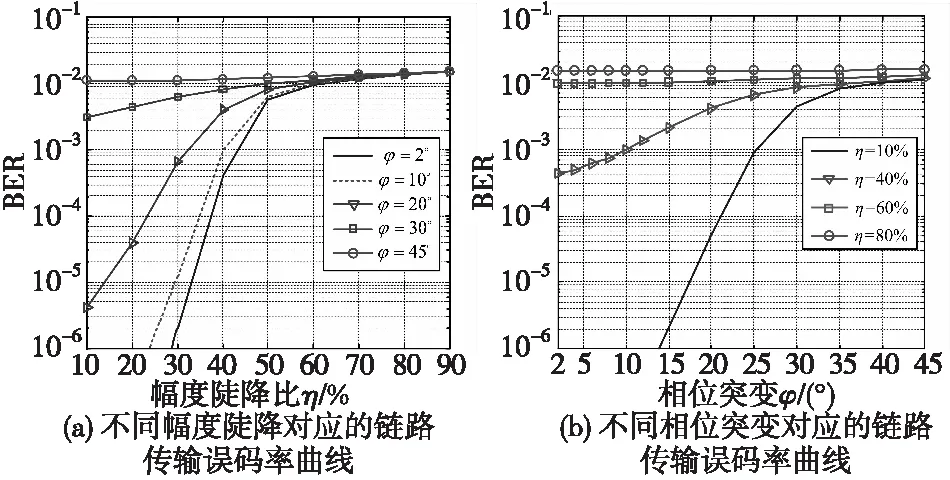
圖5 不同相位突變對應的鏈路傳輸誤碼率曲線Fig.5 BERcurves of transmission link corresponding to different phase break

綜上所述，對于QPSK和16QAM鏈路面臨信道突變，將嚴重影響信號EVM值大小，從而顯著增加鏈路傳輸的誤碼率，惡化鏈路傳輸性能。通過理論和上述仿真分析，可為實際信道突變環境的正交調制傳輸性能分析提供重要的參考依據。

4 結論

本文提出了信道突變對正交調制信號傳輸性能影響的分析方法。該方法以QPSK和16QAM等典型正交調制信號為對象，首先建立信道突變時刻對應的信號數學模型，推導得出幅度陡降、相位突變與信號EVM值、信號SNR之間的閉合數學關系式，進而計算對應的系統誤碼率。仿真實驗和理論計算結果表明，幅度陡降高于50%、相位突變大于20°均會嚴重惡化鏈路傳輸性能，誤碼率逼近10-2，為傳輸系統有效應對信道突變提供了有力的理論依據和支撐。