重疊組稀疏廣義全變分圖像去模糊方法
肖偉煌,陳穎頻
(閩南師范大學物理與信息工程學院,福建 漳州 363000)
0 引言
圖像在成像、轉換過程中經常受到運動、光學儀器工藝、噪聲等因素影響而造成圖像降質。因此,圖像去模糊是圖像處理中的經典問題[1]。
文獻[2]中廣義全變分(total generalized variation,TGV)模型,對圖像的高階梯度進行稀疏約束,能有效去除階梯效應,同時保存圖像邊緣及細節信息,是圖像去模糊的重要工具。然而,傳統TGV模型僅以L1范數對圖像的梯度稀疏性進行刻畫,沒有充分挖掘圖像梯度的鄰域結構特性,不能有效刻畫圖像梯度的局部組稀疏先驗,導致傳統廣義全變分模型在圖像邊緣保持和階梯效應抑制能力有一定局限性[3]。
為了充分挖掘圖像梯度的局部相似性,本文將一階梯度和二階梯度的鄰域信息點進行重疊組合,將重疊組稀疏(overlapping group sparsity,OGS)理論[4-9]引入TGV模型,提出了基于重疊組稀疏收縮技術的改進廣義全變分(total generalized variation based on overlapping group sparsity,TGV-OGS)圖像去模糊模型。通過該模型進一步提高平滑區域與邊界區域的差異性,保留圖像邊緣的有效信息,提高圖像去模糊效果。
鑒于提出的圖像重構模型較為復雜,計算量較大,本文引入帶重啟加速交替方向乘子(alternating direction method of multipliers,ADMM)方法[10-12]求解該模型,有效提高了圖像去模糊算法收斂速度。
在后續實驗中對比了幾種圖像去模糊方法,從實驗結果可以看到,本文提出方法取得了最佳圖像去模糊效果。
1 預備知識
1.1 二階廣義全變分去模糊模型
圖像降質過程可理解為清晰圖像和模糊核卷積運算后再加上噪聲的結果[13],即:
G=H*F+N
(1)
式(1)中,G表示觀察圖像,H表示模糊核,F表示原始圖像,N表示高斯噪聲,*表示卷積算子。
二階TGV模型不僅在去噪基礎上發揮高階變分優勢,還在去模糊方法中有效地避免了階梯效應,較好地保護圖像邊緣和細節部分,從而提高去模糊效果。
標準二階TGV模型定義如式(2)所示[13]。
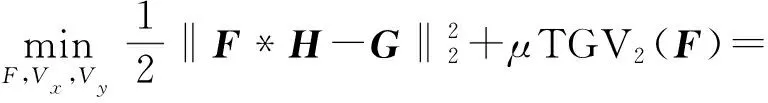
(2)
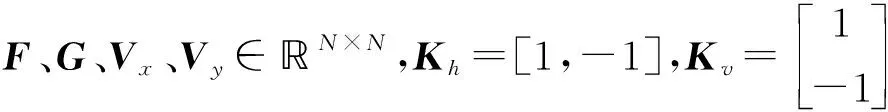
1.2 重疊組稀疏收縮算子
設V0為待收縮矩陣,可得其重疊組稀疏鄰近算子記為[6]:
(3)
(4)
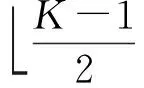
V(k+1)=mat{(I+γD2(V(k)))-1v0}
(5)
式(5)中,I∈N2×N2表示單位矩陣,v0是V0的向量形式,mat表示向量矩陣化算子,D(U)∈N2×N2是一個對角矩陣,其對角元素定義如下:
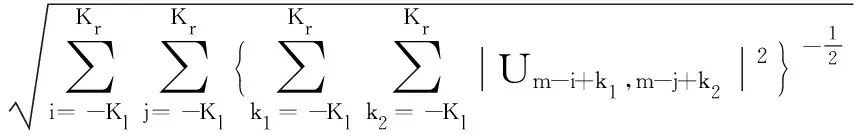
(6)
2 重疊組稀疏廣義全變分圖像去模糊方法
本章將重疊組稀疏正則項引入二階廣義全變分模型,從而充分挖掘圖像梯度的局部組稀疏先驗,提高對圖像高階梯度局部結構相似性的刻畫能力,然后在帶重啟加速ADMM框架下,將復雜問題分解成幾個解耦合的子問題求解,并加速算法收斂。
2.1 TGV-OGS模型
將重疊組稀疏的約束項來替換TGV模型中L1約束項,改進的TGV-OGS數學模型如式(7)所示:

(7)
式(7)中,TGV2-OGS(F)表示基于重疊組稀疏的二階廣義全變分約束項。
2.2 TGV-OGS模型的ADMM求解
為求解式(7)定義的改進TGV模型,利用ADMM框架對模型進行求解,該方法通過引入去耦合的分裂變量,從而將復雜問題轉化為若干個簡單的子問題進行求解。分裂變量定義為Z1=Kh*F-Vx,Z2=Κv*F-Vy,Z3=Kh*Vx,Z4=Kv*Vy,Z5=Kv*Vx+Κh*Vy。
將原問題轉化為如下問題:
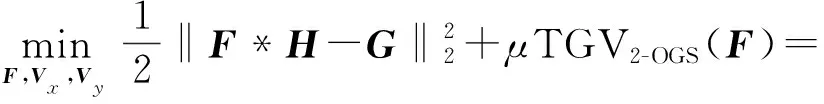
(8)
將式(8)轉化為增廣拉格朗日函數形式:
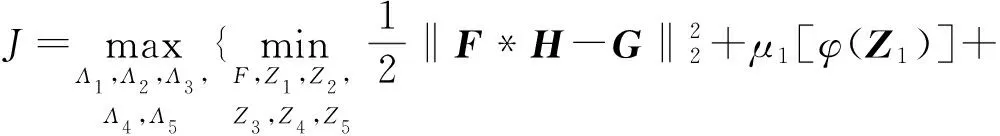
(9)
式(9)中,μ1=μα1,μ2=μα2,μ3=μα3,μ4=μα4,μ5=μα5,Λi(i=1,2,3,…,5)是拉格朗日乘子(也稱為Ζi(i=1,2,3,…,5)的對偶變量)。〈X,Y〉表示兩個矩陣X,Y的內積。
2.2.1F,Vx,Vy子問題求解
在ADMM框架下,分離變量及其對偶變量之間和三元組F,Vx,Vy是去耦合的。
對于F子問題,其子目標函數為:
(10)
利用快速傅里葉變換進行卷積計算式(10)。將式(10)轉換為頻域表達式得:
(11)
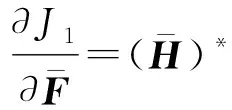
(12)
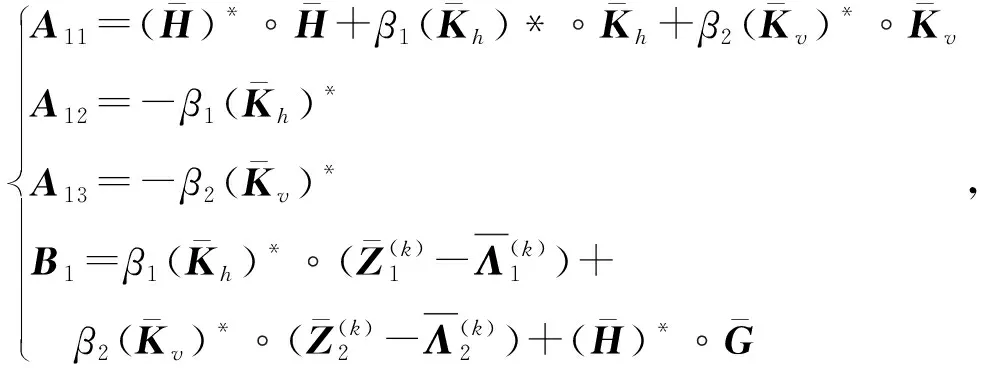
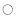
(13)
對于Vx子問題,子目標函數為:
(14)
同理,將式(14)轉換為頻域表達式得:
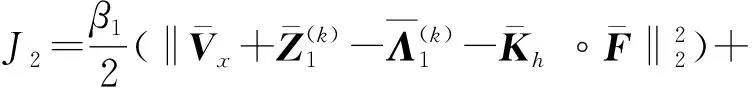
(15)
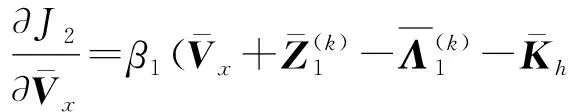
(16)
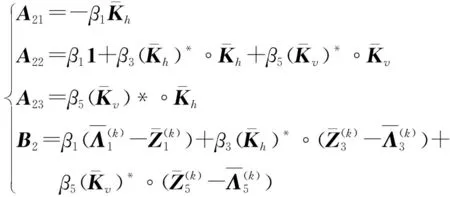
整理得:
(17)
對于Vy子問題,其子目標函數為:
(18)
將式(18)轉換為頻域表達式得:
(19)
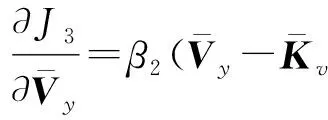
(20)

整理得:
(21)
綜合式(13)、式(17)、式(21)得到關于F、Vx、Vy三個變量的方程組,也即:
(22)
利用克萊姆(Cramer)法則與快速反傅里葉變換對F、Vx、Vy分別求解,即:
(23)
2.2.2Zi(i=1,2,…,5)子問題
對于Z1子問題,其目標子函數為:
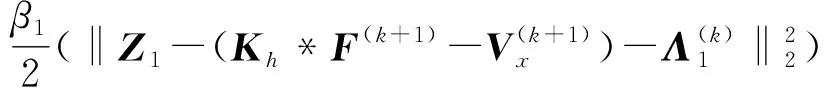
(24)
根據式(3)和式(5),可以得到Z1的更新公式為:
(25)
同理,Zi(i=2,3,…,5)的更新公式為:
(26)
2.2.3Λi(i=1,2,…,5)子問題
Z1的對偶變量為Λ1,其目標子函數為:
(27)
可以利用梯度上升法得其更新公式為:
(28)
式(28)中,γ為學習率。
同理,變量Λi(i=2,3,…,5)的更新如式(29)所示:
(29)
2.3 TGV-OGS模型的帶重啟加速ADMM求解
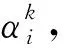
(30)
Zi(i=1,2,…,5)子問題的更新公式如下:
(31)
根據加速ADMM算法框架,Λi(i=1,2,…,5)子問題的更新公式如下:
(32)
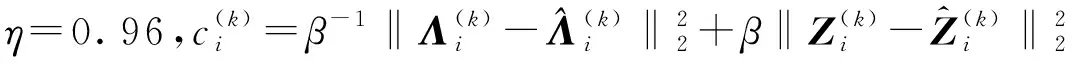
(33)
若重啟算法,將下列變量重置:
算法1為所提出模型的求解流程。
算法1 帶重啟加速ADMM框架下的TGV-OGS去模糊算法。
Input:觀測圖像G,模糊核H。
Output: 去模糊圖像F。
Initialize:
tol,Max(i=1,2,…,5).
1) While‖F(k+1)-F(k)‖2/‖F(k)‖2>tol do
2)B1,B2,B3按式(30)計算;

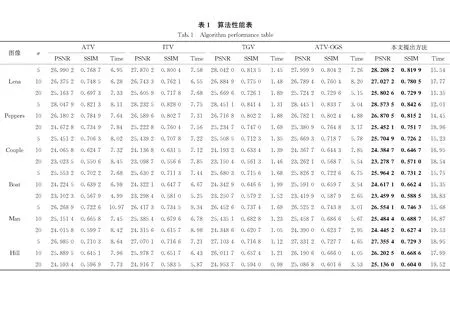
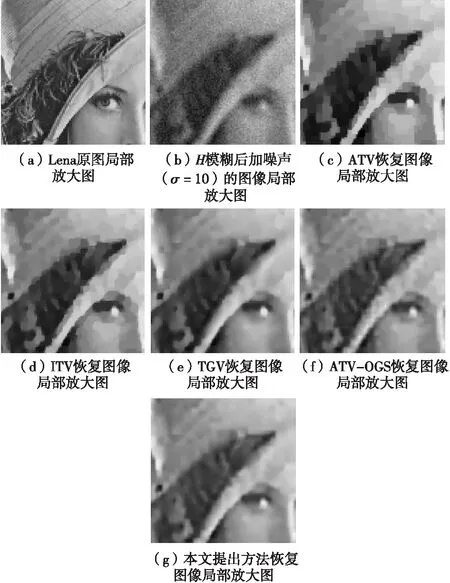
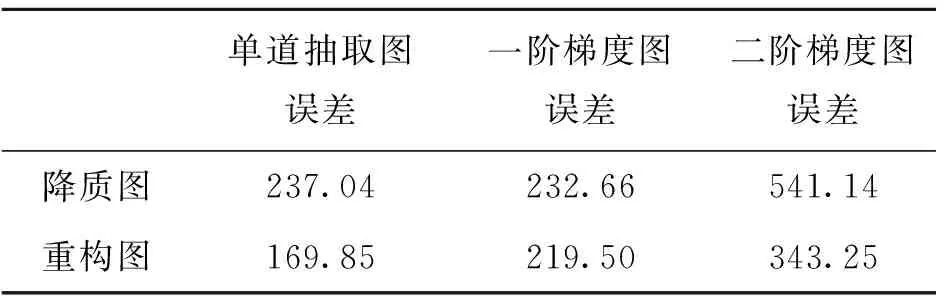
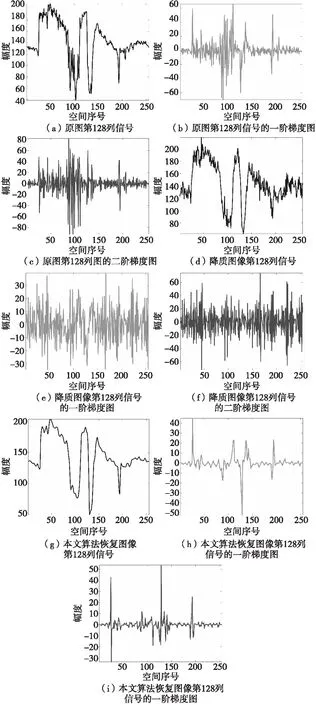
4) Whilen 7)n=n+1; 8) End While 13) Else 15) End if 16)k=k+1; 17) End While 18) ReturnF(k)asF。 本文選取了6幅圖進行實驗,如圖1所示。每幅圖像大小為256×256。 圖1 測試圖像Fig.1 Test images 實驗中使用的噪聲為高斯隨機白噪聲。在算法中,模糊核通過psf2otf(point spread punction to optical transform function)點擴散函數來構造,模糊類型為高斯模糊,模糊核大小為5×5,模糊核的標準差為5(利用Matlab指令fspecial('gaussian', [5 5], 5)產生)。實驗中,模糊核保持固定不變,將噪聲標準差σ分別設置為5、10、20。 本文涉及實驗主要對比參數為:峰值信噪比(peak signal-to-noise ratio,PSNR)[5]和結構相似性信息(structural similarity,SSIM)[14]。 以圖1為實驗測試圖像,將提出算法與各向異性全變分(anisotropic total variation,ATV)[15]去模糊方法、各向同性全變分(isotropic total variation,ITV)[16]去模糊方法、TGV[2]去模糊方法及基于重疊組稀疏的各向同性全變分(anisotropic total variation based on overlapping group sparsity,ATV-OGS)[17]去模糊方法進行對比。各比對算法去模糊指標如表1所示。表中黑色粗體標出的指標表示最優圖像恢復指標。表1顯示,本文提出方法得到的PSNR值和SSIM值均高于其他幾種比對方法,說明圖像去模糊性能最佳。但是,由于本文提出模型較為復雜,運算速度在比對算法中最慢。 圖2和圖3分別展示了Lena降質圖像的去模糊整體結果和局部放大結果。 圖2 Lena五種算法恢復對比圖Fig.2 Recovered image comparison 圖3 Lena五種算法恢復圖的局部放大圖Fig.3 Recovered image comparison 圖2中,模糊核如圖2(c)所示,模糊后的圖像被高斯白噪聲(σ=10)進一步污染。觀察圖3可知,本文提出方法相比于其他方法更好地壓制了階梯效應。 圖4反映了算法對圖像一階梯度和二階梯度的約束效果,從圖中可以看到,本文提出方法有效壓制了受污染圖像一階和二階梯度的噪聲,并保留了原圖像一階、二階梯度中的最大值,從而較好地恢復出圖像。對比圖4(a)、(d)、(g)可以發現,該方法有效地去除了尖峰和毛刺,恢復出來的圖像去模糊效果相比其他去模糊方法得到了一定程度提升。 表2將圖4(d)、(e)、(f)和圖4(g)、(h)、(i)關于圖4(a)、(b)、(c)的誤差進行對比。從表中可以看到,提出方法的單道抽取圖、抽取圖的一階梯度和二階梯度誤差均小于污染圖像三條曲線關于原圖三條曲線的中心誤差。 表2 誤差對比Tab.2 Error contrast 圖4 單道對比圖Fig.4 Single signal comparison 圖5反映了迭代過程中,恢復圖像的相對誤差(relative error,RE)變化趨勢,其中RE=‖F(k)-F‖2/‖F‖2,F表示原圖像,F(k)表示算法恢復圖像。從圖中可以看到,隨著算法不斷迭代,恢復圖像和原圖的誤差逐步減小,且算法收斂得非常迅速,在第5次迭代以后,RE曲線就趨于平緩。 圖5 算法動態迭代圖Fig.5 Dynamic iteration image 本文提出了基于重疊組稀疏收縮技術的改進廣義全變分模型去模糊方法。該方法能更充分地挖掘圖像一階和二階梯度的鄰域結構相似性,從而進一步提升了TGV模型的性能。實驗結果表明,該方法能有效抑制恢復圖像中的階梯效應,提高對圖像高階梯度局部結構相似性的刻畫能力,從而提高圖像去模糊效果。數值計算方面,利用帶加速重啟的交替乘子迭代法求解提出模型,有效提高算法效率。實驗結果表明,提出方法的圖像重構質量在所有比對算法中達到最佳效果,且算法在迭代少數步數后快速收斂。值得注意的是,本文提出方法也存在一定的局限性,本文算法復雜度較高,在實時處理圖像方面存在不足。 本文所提出的正則項可應用于椒鹽噪聲、指數噪聲、柯西噪聲等其他噪聲背景下圖像的去模糊問題,我們將在未來的工作中進一步討論。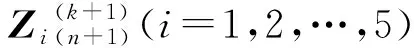
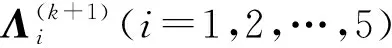
3 實驗與分析
3.1 實驗說明

3.2 算法性能對比


4 結論

