飛機螺栓雙剪連接結構有限元應力分析

陳彥達 范振民 李 軍

（1.東航技術應用研發中心，上海 201707；2.上海飛機設計研究院，上海 201210）

0 引言

機械緊固接頭是航空航天領域中連接結構部件最常用的方法，如機翼結構中的蒙皮—梁/肋板連接、機翼—機身連接是飛機主結構中螺栓連接的典型示例。螺栓緊固件能夠很好地將連接件夾緊在一起，并且具有良好的承載能力。一些研究人員[1-4]詳細介紹了螺栓連接的設計方法主要是在靜態載荷條件下，但是在構件上鉆出緊固件孔本身會在孔附近引入應力集中并減小承載橫截面積，鉆孔過程也會影響緊固件孔內部的表面光潔度，這在循環載荷下容易產生疲勞裂紋。

飛機結構主要由高強度輕合金和復合材料制成，材料的低密度性能使它們成為了理想的強度/重量比航空航天材料。安全性在航天飛行器中是至關重要的，因此已經進行了大量研究，旨在優化結構螺栓連接的設計，從而防止飛行過程中的災難性故障[5-11]。

螺栓連接通常通過初始扭矩進行預加載，當扭矩施加到螺母上時，螺栓被軸向拉伸，機械構件被夾緊在一起。以往的研究證實，當接頭承受縱向拉伸載荷時，螺栓的夾緊效應可以降低螺栓孔處的應力集中，從而增加接頭的斷裂強度和疲勞強度[12-16]。基于有限元分析結果，發現預緊力可以在單個夾板的螺栓孔周圍引入有益的壓應力，且施加的預緊力越高(在一定程度內)，在孔區域的壓縮應力的幅度越大，這種壓應力可以減小在所施加的拉伸載荷下產生的合成應力的大小。此外，還發現在循環加載條件下，預緊力大幅度增加可能會導致配合面螺栓板的表面產生微動現象[16-17]。

隨著緊固件的被夾緊，確定螺栓連接中的局部應力分布通常是三維問題，有一些方法可用來根據夾緊區域內壓力分布的常規假設來估計接頭構件的剛度[18-19]。R?tscher[18]提出，應力包含在接頭中平面對稱的兩個圓錐形截面內，每個截面的頂角都是2α，然后選擇α=45°的半頂角來計算剛度。在之前所述研究[9]中討論了雙圈鋁制螺栓連接結構的有限元計算結果，并展示了夾緊板的整體壓力分布，包括在外板上形成的一對圓錐體和一個沿中間板厚度均勻分布的中空圓柱體。據研究，有限元法是一種用來確定和分析螺栓連接的應力和應變的方便而有效的方法，然而，文獻綜述證實[9]，由于預緊力和拉伸載荷而引起的螺栓連接的三維應力分析非常復雜，并且還沒有被進行徹底的研究。

本研究的主要目的是確定飛機雙搭接鋁制螺栓連接處的應力和應變分布，以便預測這種連接的失效模式。在設計和生成結構三維有限元模型后，模擬螺栓預緊力，隨后在板遠端施加拉伸載荷，為了改善飛機金屬和復合材料結構中的螺栓連接設計，研究并討論了孔區域產生的應力和應變結果。

1 有限元建模過程

使用CATIA三維軟件設計了雙搭接螺栓連接結構，結構幾何形狀和尺寸如圖1 所示。該結構包含三塊相同的鋁合金7075-T6 板，厚度均為3 mm，孔的直徑為5 mm，并選擇直徑為4.9 mm的標準航空航天螺栓緊固件(AN3-6A)來夾緊鋁合金板。在本算例中，由于兩個笛卡爾平面的幾何結構和載荷條件是完全對稱的，所以只對其四分之一進行數值分析，如圖2 所示，并且為這些對稱平面上的節點定義了對稱位移邊界條件。

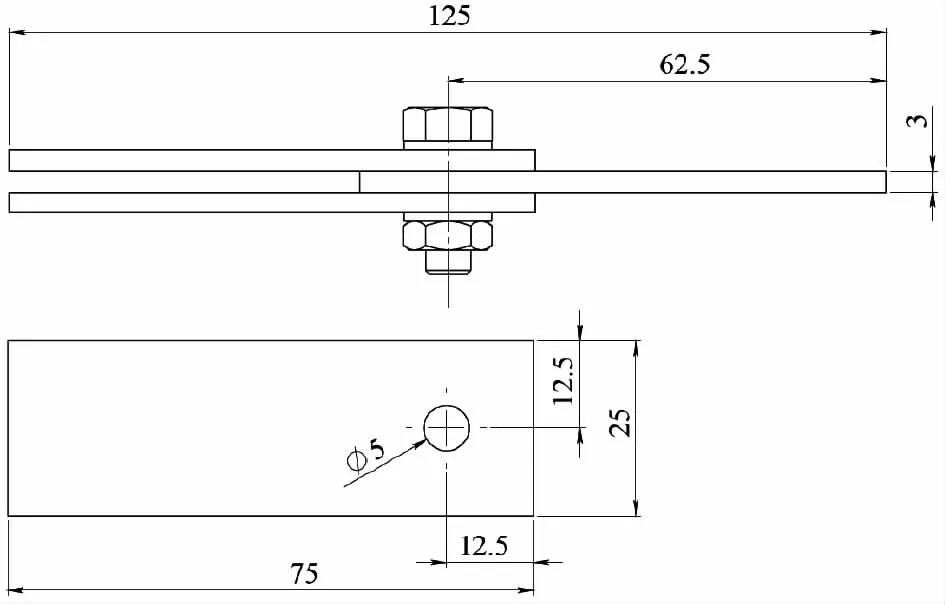
圖1 接頭幾何及尺寸示意圖 單位:mm

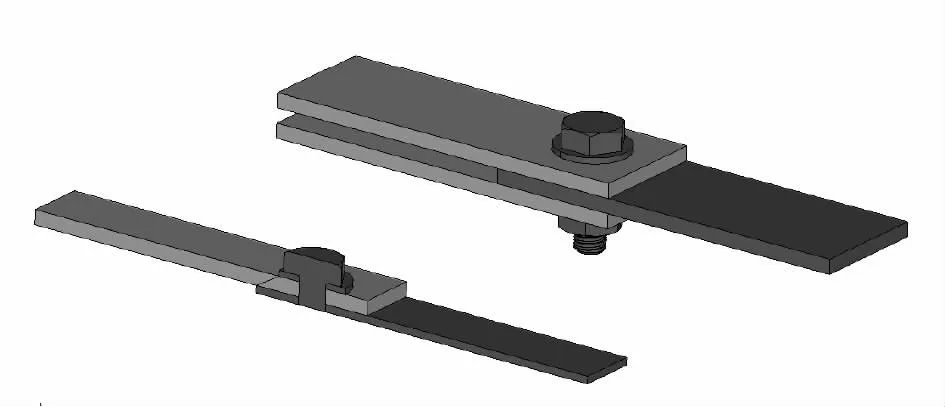
圖2 結構完整模型和四分之一模型

在本文中，將螺栓的幾何形狀定義為圓形的螺栓頭，而不是六邊形。由于螺栓和墊圈的彈性模量和泊松比幾乎相同，將外徑為10 mm、厚度為0.75 mm的墊圈與螺栓頭幾何模型合并成一個整體，以減少接觸單元的使用(忽略螺栓頭和墊圈之間的接觸)。根據參考文獻[20]，受剪力接頭處螺栓桿的夾緊長度應接近被緊固構件的總厚度，因此根據航空航天AN螺栓標準尺寸，螺栓建模時的緊固長度為9 mm。此外，在這里暫時不需要考慮螺紋建模，如圖3 所示，假設螺栓桿和緊固件孔之間的徑向間隙為0.10 mm。

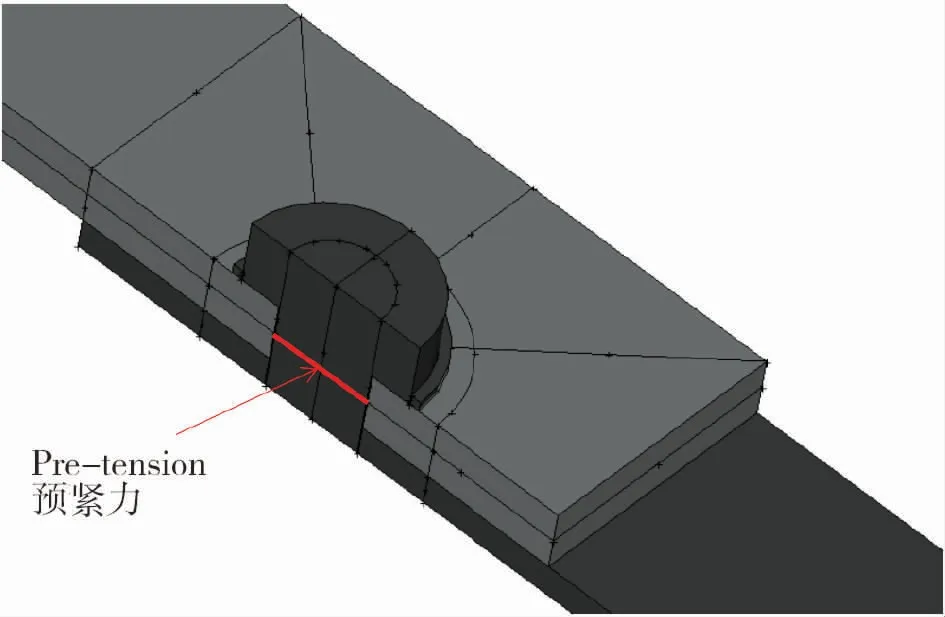
圖3 預緊力模擬

為了達到最優的網格密度，對板和螺栓的幾何模型進行虛擬分區，然后對單元劃分進行多次修改，以實現應力計算結果的網格不敏感性。圖4 顯示了最終的結構網格模型。

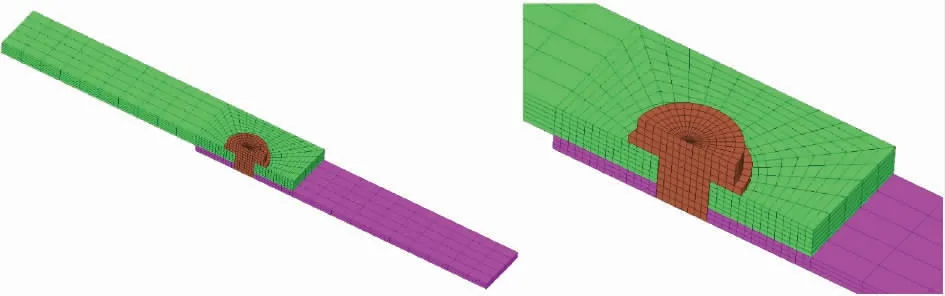
圖4 有限元網格模型

由于考慮到結構將受到不同水平的縱向載荷，采用彈塑性多線性運動硬化材料模型對鋁合金7075-T6 的應力—應變行為進行了表征。選擇這種材料來計算材料塑性區域中的應力和應變，特別是在中間板的孔周圍位置。薄鋁板由于軋制過程顯示出正交異性行為，在某些情況下，這種差異可以達到10%，但在本研究中給忽略了這種正交效應。鋁合金7075-T6 的應力—應變曲線如圖5 所示[16]，并將此圖的7 個數據點作為模型材料的輸入參數，如表1 所示，彈性模量和泊松比分別為E=710 GPa和v=0.33。對于鋼制螺栓和墊圈，采用彈性模量為210 GPa，泊松比為0.30 的線彈性材料，這是基于所測試的數據，即螺栓材料在受到最大給定扭矩(5.5 N·m)[9]時仍處于彈性變形區域(沒有塑性變形)。

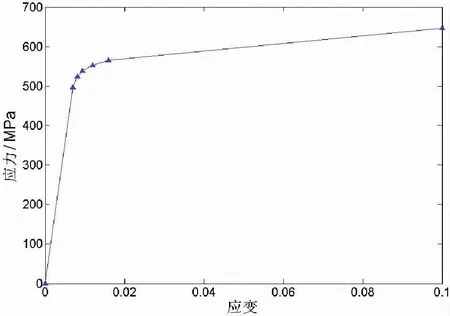
圖5 鋁合金7075-T6 應力—應變曲線圖

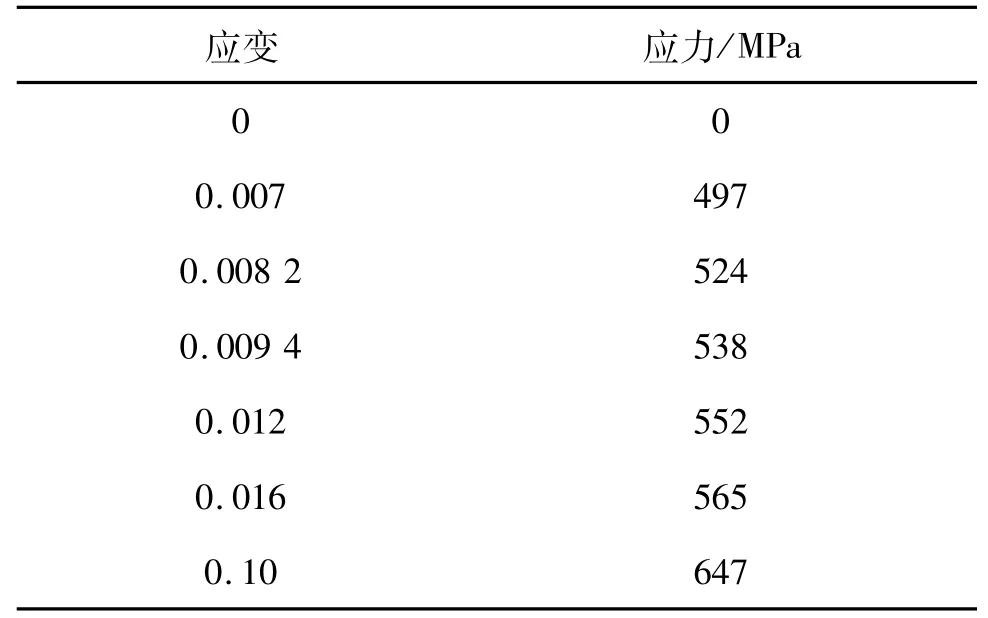
表1 7075-T6 應力—應變曲線數值

所有接觸表面之間的摩擦系數在模型中被考慮，這里使用彈性庫侖摩擦模型。將鋼制螺栓(頭部和柄部)與鋁板之間的摩擦系數設置為0.23，頂部和中間的板之間摩擦系數設置為0.22，模型中所有接觸表面之間的4 個不同的接觸對如表2所示。

表2 接觸對設置

接下來施加預緊力和縱向拉伸載荷，并為接頭模型定義了兩個不同的載荷步。實體螺栓模型作為真實的有限元模型，拉伸、彎曲等載荷通過螺栓進行傳遞[9，21]，參考文獻[9]采用實心螺栓建模，在ABAQUS 中通過Pre-tension 來模擬預緊力(如圖3所示)，預緊力大小分別為2 kN、4 kN和6 kN。之后，對于具有特定預緊力的每個待解決的模型，在接頭處施加15 kN的縱向遠程拉伸載荷，因此，在第二個載荷步中，相應的遠程應力在x方向靜態地施加到中間板的遠端(遠離孔)，這個壓力分為15 個子步驟遞增的方式施加，目的是獲取所有1，2，3，...，15 kN拉力下對應的應力值的數值結果。除了對稱的位移邊界條件之外，頂板的端部也受到所有自由度的約束。

2 計算結果及討論

夾緊區域內的縱向正應力有限元計算結果表明，在接頭處的應力整體呈瓦片形狀分布，這些結果在以前的工作中已經經過了討論[9]。根據計算結果，預緊力的大小對接頭的抗拉強度有影響，并且由中間板產生的縱向法向應力(σx)的分量大小來表示。對模型施加不同的預緊力，分析中間板最大應力在不同預緊力下的σx，如圖6 所示，可以發現即使對于最大的預緊力，壓縮應力也不是很大，當接頭受到遠端施加的縱向拉伸載荷時，這個應力分量可以起到控制合成應力的關鍵作用。

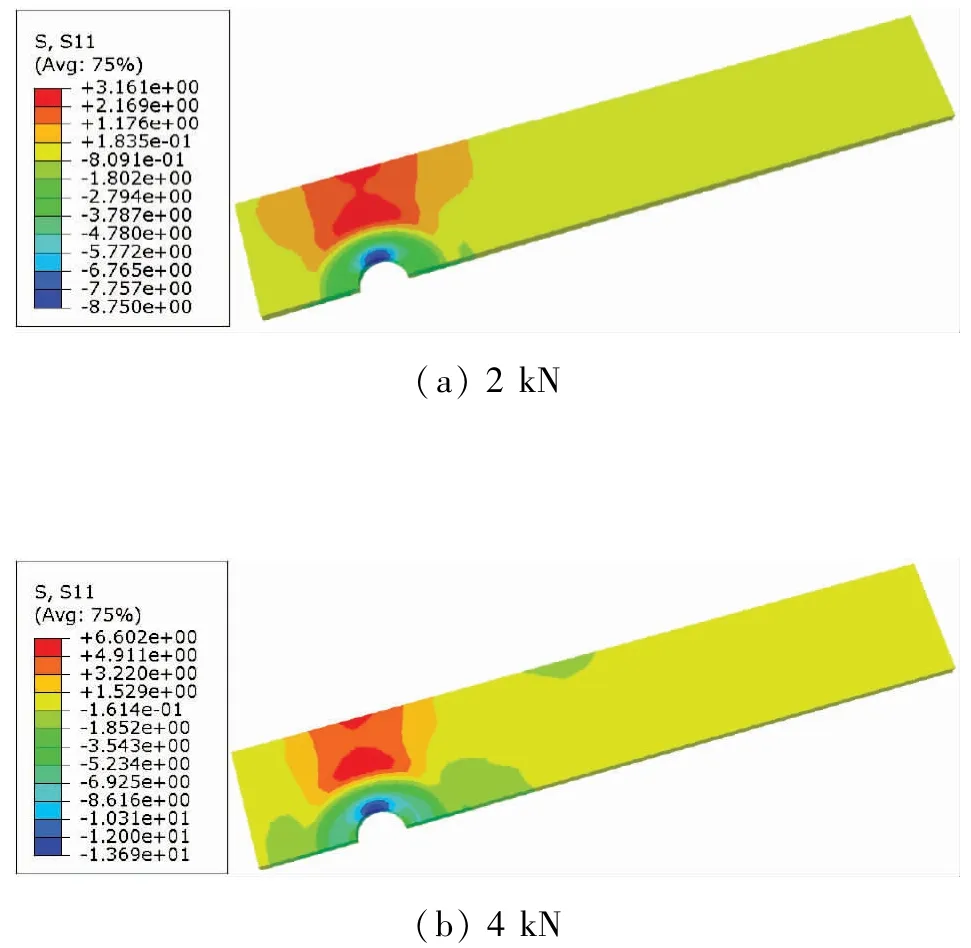
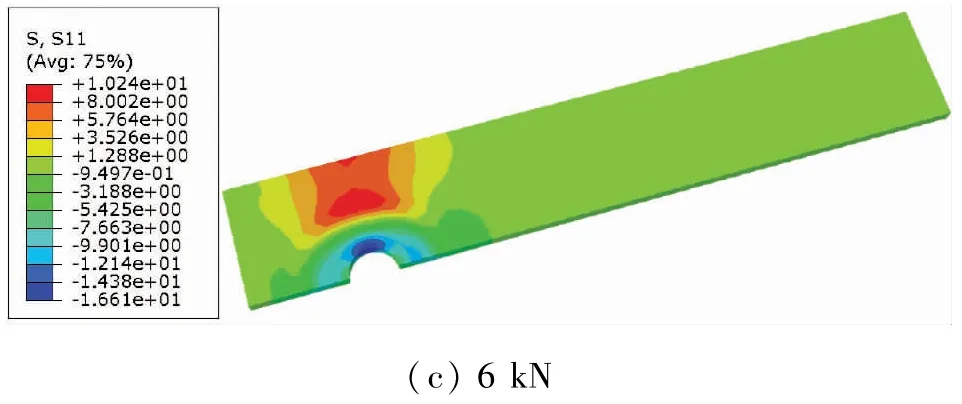
圖6 中間板縱向應力σx最大值在不同預緊力作用下 單位:MPa

在對不同預緊力的有限元模型施加1，2，3，...，15 kN共15 個縱向拉伸載荷子步驟之后，對接合處進行數值分析。圖7 表示在15 kN的縱向拉伸載荷和預緊力為1 kN的情況下，中間板合成縱向應力(σx)的分布圖。如應力云圖所示，最大拉應力位于孔的邊緣處，特別是由于缺口存在而導致出現局部應力集中的中間板，這也反映了為什么在金屬雙搭接螺栓連接結構中的中間板容易發生破壞。另外，為了傳遞施加在接頭上的壓縮載荷，在螺桿和板之間接觸的區域也存在著較大的壓縮應力，在正交各向異性復合材料板中，應力結果也會受到中間板的纖維取向和疊層順序的影響[5，10]。

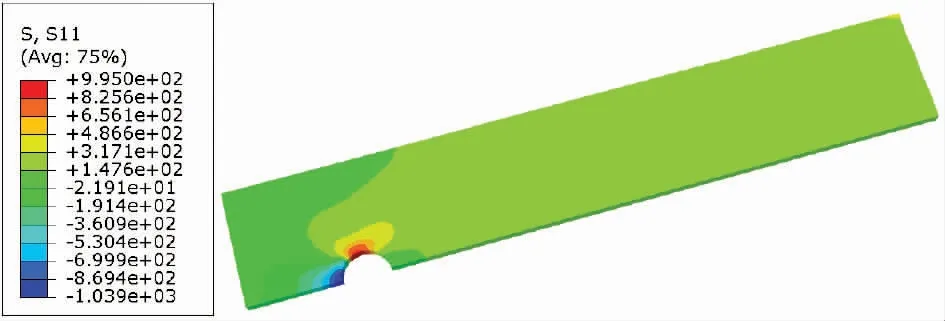
圖7 中間板在1 kN預緊力和15 kN縱向拉伸載荷下的縱向應力分布(σx) 單位:MPa

根據Shankar和Dhamari[16]的研究結果，在緊固件孔附近，類似的雙搭接螺栓板最終斷裂發生在中間板上，圖8 顯示了在1.15 kN預緊力作用下，試件中間板在最大應力為144 MPa和載荷比為0.1 的循環載荷下發生的疲勞失效。不合格試件的斷裂指示疲勞在應力局部集中的孔邊緣開始，斷裂線穿過緊固件孔的中心線。該試驗與獲得的有限元模擬計算結果的對比具有很好的一致性，并且驗證了結構的有限元建模是合理的。

圖8 試件中間板在預緊力為1.15 kN、縱向拉伸應力為144 MPa下的疲勞破壞[16]

對上述45 個模型計算得到的σx應力結果進行比較，揭示出較大的預緊力可以大大減少應力集中和孔周圍的壓縮應力，數據對比結果如圖9 所示。例如，模型在2 kN預緊力和10 kN縱向拉伸應力作用下時，中間板孔邊緣的最大拉伸應力(σx)是647 MPa；然而，當預緊力增加到6 kN時，該應力顯著降低到524.2 MPa。同樣的情況下，中間板孔邊緣最大壓縮應力(σx)從764 MPa減少到630.6 MPa。需要注意的是，在某些加載情況下，鋁板的應力大小超過了材料模型應力—應變關系的極限值，這是因為在ABAQUS 中通過簡單地外推曲線來分析這些大的應力和應變。

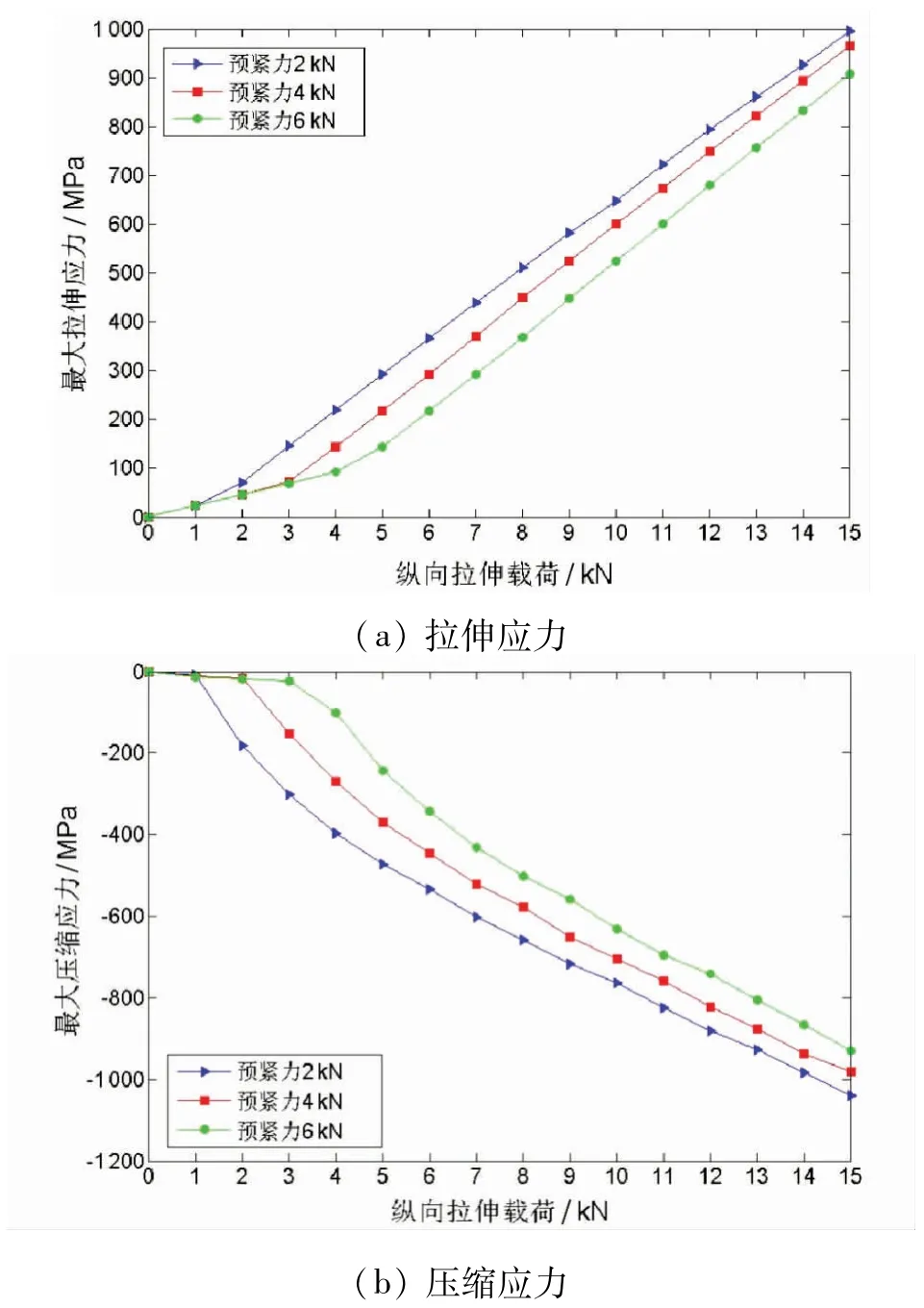
圖9 在不同預緊力和縱向拉伸載荷下的中間板孔邊緣處最大應力值

為了從數值上發現隨著預緊力的增加可以減少局部應力，對不同預緊力模型的拉伸和壓縮應力最大值的減少百分比進行了平均，結果如表3 所示，可以發現，當預緊力從2 kN增加到6 kN時，將使中間板的最大拉伸應力和壓縮應力分別減小26.93%和30.42%。如之前所述，為了研究7075-T6 板受局部應力下的夾緊效應，使該結構承受不同水平的縱向拉伸載荷，在圖10 中分別顯示了施加2 kN和6 kN的預緊力模型，在受到9 kN縱向拉伸載荷下的Von Mises應力云圖。可以發現，通過施加較高的預緊力，孔邊緣的應力幅值較小，因此當施加在遠離接頭的縱向拉伸載荷相對較高時，塑性應變也較小，它將Von Mises塑性應變的最大值從1.32 ×10-2減少到1.05 ×10-3，共減少了12.55 倍。

表3 隨著預緊力的增加拉伸應力和壓縮應力的平均減少百分比

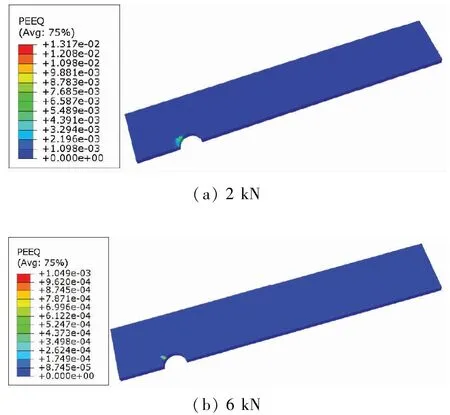
圖10 縱向拉伸載荷為9 kN時，不同預緊力作用下中間板孔邊緣的塑性應變 單位:MPa

此外，對于預緊力最大(6 kN)而縱向拉伸載荷較小(小于3 kN)的模型，最大拉伸應力(σx，max)出現在遠離孔邊緣的位置，如圖11 所示。在這種情況下，可以認為由于較高預緊力所產生的壓應力可以成功克服由于施加較小的拉伸載荷而導致的局部應力，因此，最大拉伸應力不一定發生在孔邊緣處。實際上，通過較大的預緊力來緊固接頭，產生了較大的法向力來壓縮接合板，并因此在配合表面之間產生了較大的摩擦力，由于施加的縱向拉伸載荷較小，所以這些板貼合地非常緊密，因此，大部分的載荷是通過摩擦來傳遞的，而不是螺桿和孔邊緣區域的板之間的壓縮應力。

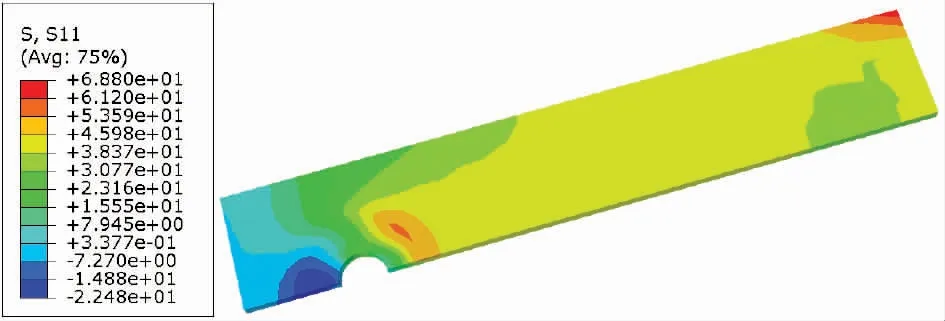
圖11 在6 kN預緊力和3 kN縱向拉伸載荷下中間板的縱向應力分布(σx)及最大拉伸應力的位置 單位:MPa

高預緊力對結構承載的好處，很大程度上取決于結構之間的摩擦，但工程結構設計中，摩擦力所帶來的好處通常是不允許考慮的。因此本文還計算了在沒有摩擦的前提下，預緊力帶來的應力變化，如圖12 所示。

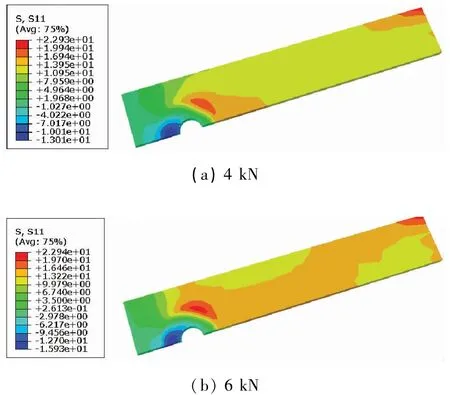
圖12 不考慮摩擦且縱向拉伸載荷為1 kN時，不同預緊力作用下中間板應力 單位:MPa

通過進一步的對比發現，在不考慮螺栓和板之間的摩擦力時，當預緊力從4 kN提升到6 kN，縱向拉伸載荷為3 kN時，最大拉伸應力減少的比例為2.68%，而在有摩擦的情況下這一比例為5.1%。當縱向載荷增加到4 kN時，無摩擦和有摩擦兩種條件下最大拉伸應力下降的比例分別為35.8%和35.25%。

3 結論

本文利用ABAQUS 有限元分析軟件，對典型的飛機螺栓連接結構進行了三維應力和應變分析，提出了一種有限元建模技術，模擬了螺栓連接中的預緊力，根據之前的研究結果成功地驗證了該方法的有效性，并對緊固件受預緊力大小的影響進行了研究，結論如下：

1)施加預緊力可以在螺栓孔周圍引入有益的縱向壓縮應力，從而減少孔邊緣處由于局部應力集中產生的合成應力。這些應力在螺栓連接位置處更為集中，并且可以有效減小在施加遠端縱向拉伸載荷下的產生的結構變形。

2)數值分析結果表明，對于在施加縱向拉伸載荷下的螺栓連接結構，較大的預緊力將更有利于降低緊固件孔邊緣處的應力集中，這可以顯著提高接頭的拉伸強度和疲勞壽命。

3)這項研究工作證明，即使在較大的縱向拉伸載荷下，施加較大的預緊力來牢牢夾緊緊固件接頭，可以通過改變結構載荷傳遞，將壓縮應力轉化為摩擦力來有效地減少緊固件孔處壓縮應力的破壞效應。這可以成功地防止高負荷結構螺栓連接處的承壓損壞，特別是對于主要失效機理是纖維微屈曲的組合結構中。對復合材料層壓進行上述分析也將是有意義的，在進行損傷演化[22]和疲勞強度評估方面，了解貫穿整個板厚的應力幅值大小十分重要。