非接觸水下爆炸下艦船沖擊環境的不確定度量化

梁霄，陳江濤，王瑞利，胡星志

1 山東科技大學 數學學院，山東 青島 266590

2 中國空氣動力研究與發展中心，四川 綿陽 621000

3 北京應用物理與計算數學研究所，北京 100094

0 引 言

艦船非接觸水下爆炸是一系列復雜的非線性多物理過程，迄今仍無法得到全系統、全時空的理解[1-4]。在研究水下爆炸時，主要運用3 種方法：試驗、理論計算和數值仿真[1,3,5-6]。二戰后，西方海軍強國通過實船水下爆炸試驗[7-8]來直觀地觀測爆炸毀傷效果和評估船船抗沖擊性能，以此判斷擬定設備裝艦的可行性。然而，實船水下爆炸試驗也存在固有缺陷，例如成本高昂、過程不可控、對海洋生態環境造成破壞等。數值仿真的優點是安全環保、成本低、過程可控，但建模和模擬（M&S）過程中卻包含了大量不確定性因素，使得決策者對M&S 方法的預測能力有所顧慮。

不確定度量化（uncertainty quantification，UQ）技術結合了試驗與數值這2 種方法的優點，運用此技術可提高數值模型的可信度和可靠性。近年來，UQ 研究作為一門新興學科，受到了歐美國家學者的高度關注，被廣泛應用于核能[9-11]、安全[12-13]、航空航天[14-18]等重大工程領域。我國在實船水下爆炸試驗領域起步較晚，可獲得的樣本有限，供借鑒的國外公開資料也極度匱乏，使得我國艦船非接觸水下爆炸的UQ 方法研究具備了廣闊的應用前景。然而，有關艦船非接觸水下爆炸的UQ 研究至今未見相關報道，其中部分原因是水下爆炸的M&S 過程復雜而獨特，且無法照搬已有的成熟方法。

首先，由于水下爆炸M&S 過程中不確定性因素繁多且類型不同，除了有物理量自身固有的波動性和測量技術誤差導致的無法消除的不確定度外，還有基于擬合數據的需要，在上述過程中使用了沒有物理意義的不確定度且無法通過試驗標定的唯象參數； 其次，目前常用的UQ 方法成立的前提條件是隨機變量服從獨立同分布（independent identical distribution, IID），但水下爆炸中的隨機變量并不完全服從獨立同分布； 再次，部分不確定的物理量要求嚴格非負，使得概率統計中常見的高斯分布無法直接應用，例如，若假設質量服從正態分布，則理論上樣本取值會出現質量為負的非物理情況； 最后，若假設參數服從均勻分布，則容易滿足參數的有界性要求，但均勻分布的概率密度函數的強間斷性使其很難轉化為正態分布。因此，選取合理且符合統計結果的概率分布，對艦船非接觸水下爆炸的UQ研究至關重要。

對于UQ 方法的選擇，很自然地會想到蒙特卡洛（Monte Carlo，MC）方法，但 MC 方法有著收斂速度慢的缺陷，而能有效代替MC 方法的是多項式混沌（polynomial chaos，PC）方法，它也是大規模工程計算中常用的方法[19-23]。然而，在艦船非接觸水下爆炸M&S 過程中有太多的不確定性因素，使得多元PC 方法容易陷入“維數災難”。簡言之，若采用經典的5 個求積點方法計算11 維隨機變量驅動的水下爆炸系統，則需要運行程序511≈ 4.9×107次，5 階多項式則需要展開（PC 截斷長度[24]）(11+5)!/(11!5!)-1=4 367次 ，共需運行程序約5×1011次，超出了目前的計算能力。而基于自適應基函數的齊次Wiener混沌方法改進了PC 方法，可緩解“維數災難”問題，其核心思想是通過構造隨機基函數的同構酉變換（unitary transformation）得到新隨機基函數，待測物理量在新隨機基函數展開下的概率集中在低維子空間。

鑒于此，本文將重點研究使用基于自適應基函數的齊次Wiener 混沌方法處理含高維不確定度的艦船非接觸水下爆炸問題。通過設計一個簡單的試驗裝置，給出系統輸出量的期望值、標準差、置信區間等統計信息，進而分析、量化和評估不確定性因素對非接觸水下爆炸下艦船沖擊環境的影響，所得結果可提高數學模型的可靠性、可信度和預測能力，用以為船舶結構設計和設備上艦安裝提供依據。

1 數學物理模型

因為水下爆炸的壓力與時間及位置有關，且不容易通過實測獲得，所以需要通過如下經驗公式來確定[1-2,25]。

美國海軍艦載設備的抗沖擊性能是艦船結構設計及設備裝艦的依據。如圖1 所示，在艦船-水交界面（流固耦合處），入射波分解為2 個部分：一是穿透甲板的折射波；二是反射回水中的反射波。反射后的凈壓力是入射波和反射波的代數運算結果。

圖 1 試驗裝置受力分析Fig. 1 Force analysis of experimental setup

2 不確定度挖掘、量化和傳播

2.1 不確定度來源和量化

在非接觸水下爆炸與艦船相互作用的過程中，存在眾多不確定性因素，且可分為2 類：一類是不確定的物理量；另一類是不確定的唯象參數（也稱“擬合系數”）。表1 中， ξ1～ ξ6為可通過試驗標定的不確定物理量； 表2 中， ξ7～ ξ14為無法通過試驗標定的不確定唯象參數，。

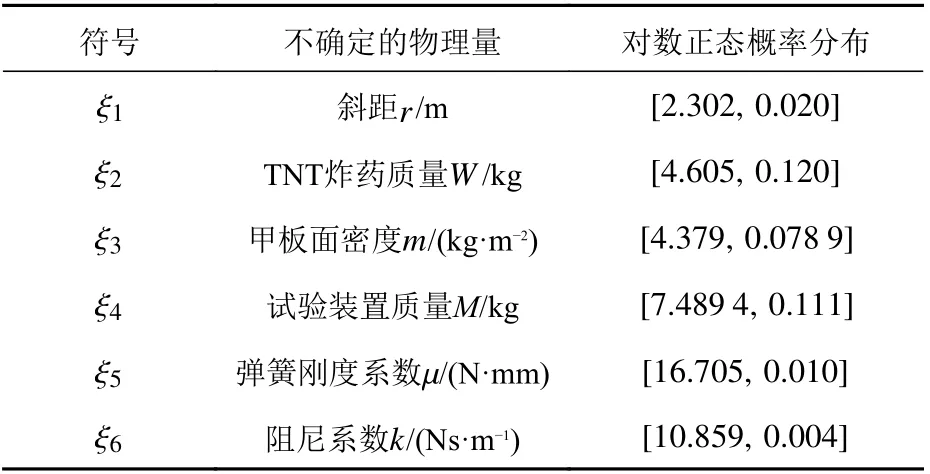
表 1 艦船非接觸水下爆炸中的不確定度（物理量）Table 1 Uncertainty of ship subjected to non-contact underwater explosion（physical quantities）

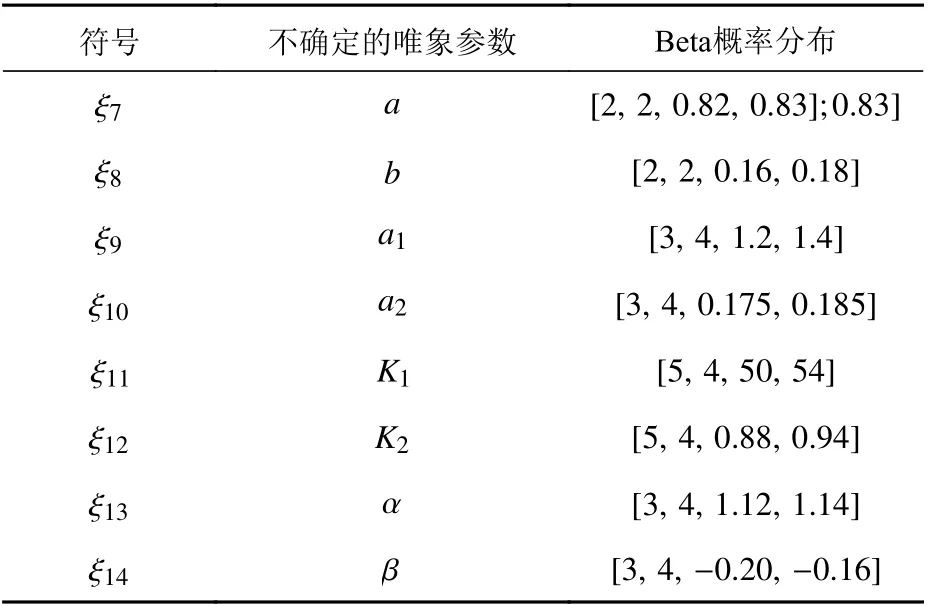
表 2 艦船非接觸水下爆炸中的不確定度(唯象參數)Table 2 Uncertainty of ship subjected to non-contact underwater explosion（empirical parameters）

2.2 Rosenblatt 變換

二次自適應基函數齊次Wiener 混沌方法成立的前提是隨機變量必須是滿足獨立同分布的標準正態隨機變量，但由2.1 節可知，此條件并未得到滿足。本文使用Rosenblatt 變換[26]將相關隨機變量轉化為服從標準正態分布的獨立隨機變量組。具體步驟為：設 {X1, X2, ..., Xn}為一列隨機變量（其中下標n 為隨機變量的個數）。令

圖 2 隨機變量的概率密度函數Fig. 2 Probability density function of random variables

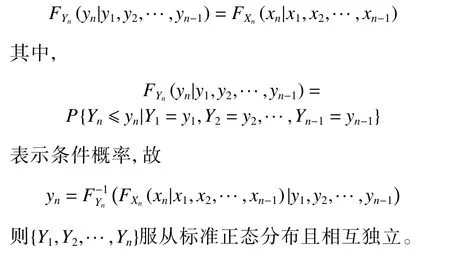
2.3 帶有二次自適應基函數的Wiener 混沌理論

3 不確定度量化結果分析

由圖6 還可見，隨著時間的變化， z(t)的變化范圍越來越窄，PDF 峰值增加，而偏度則交替出現。綜上所述，采用本文方法對長時間的動力行為進行預測要比初始階段容易一些。

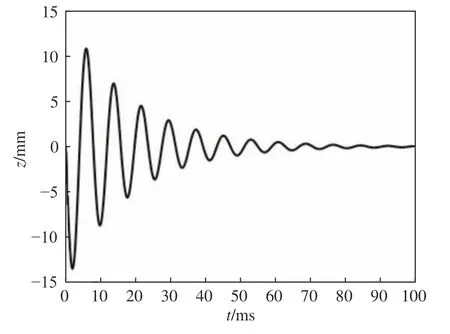
圖 3 彈簧系統位移z 的期望值Fig. 3 Expectation for displacement z in spring system

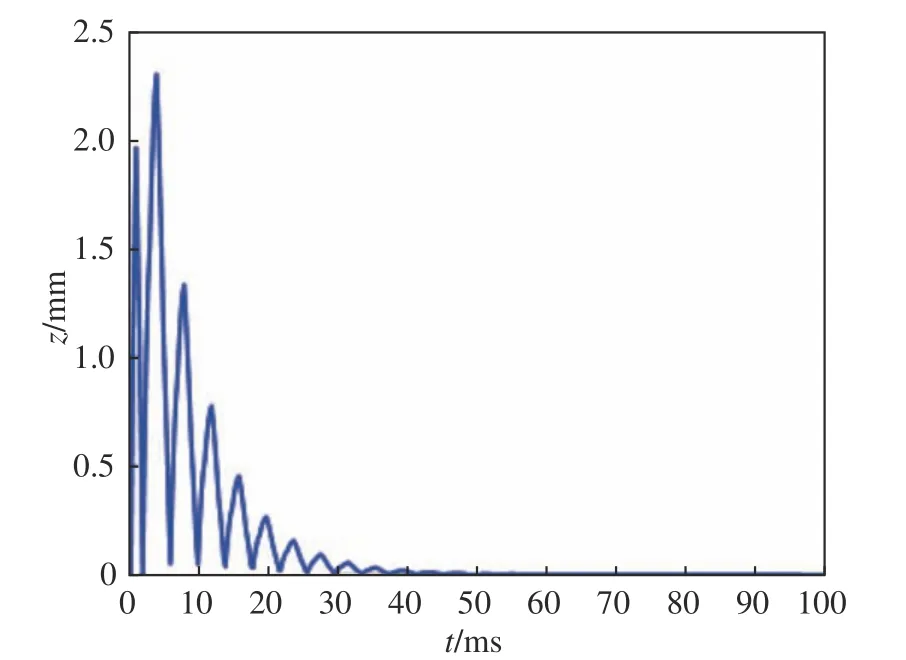
圖 4 彈簧系統位移z 的標準差Fig. 4 Standard deviation for displacement z in spring system

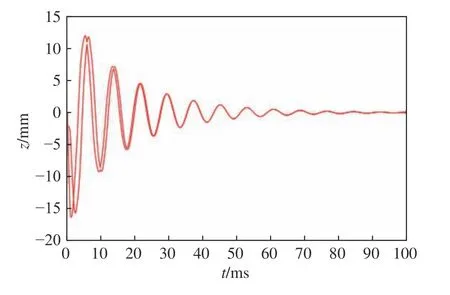
圖 5 彈簧系統位移z 的置信區間Fig. 5 Confidence interval for displacement z in spring system

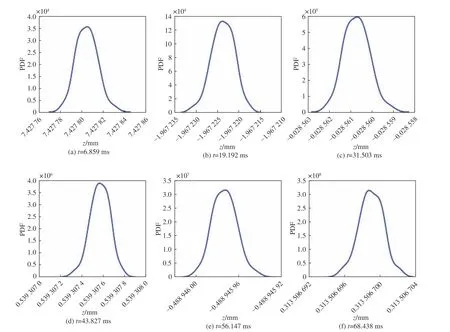
圖 6 不同時刻彈簧系統位移z 的概率密度函數Fig. 6 PDF of displacement z in spring system at different times

4 結 論

本文通過設計合適的彈簧系統試驗裝置，應用概率統計方法研究了中、低強度水下爆炸的不確定性因素對甲板上彈簧系統試驗裝置的影響。利用基于自適應基函數的齊次Wiener 混沌方法，給出了試驗裝置位移的期望值、標準差、置信區間以及概率密度函數。得到如下主要結論：

1） 甲板受到水下爆炸沖擊波的沖擊后，一直處于振蕩狀態。彈簧系統試驗裝置的期望值和標準差在達到極大值后逐漸趨于0，置信區間也逐漸變窄。標準差的振蕩相比期望值大很多，且標準差達到極值的時間落后于期望值。因此，當艦船受到非接觸水下武器的攻擊時，爆炸沖擊初始階段的毀傷效果最大且不易預測，此時的艦船防護至關重要。

目前，土地面積測算的方法有解析法與圖解法兩種[7]。其中解析法利用高精度的界址點計算土地面積，是一種較精確的土地面積量算方法，即用界址點的坐標按相應公式計算土地面積。界址點的坐標測量有導線測量、三角測量或GPS測量[8]。本文選用GPS測量進行特征點的坐標測定，然后通過CASS9.0軟件的表面積計算與實體面積計算功能進行河道綠地面積的計算。

2） 基于自適應基函數的齊次Wiener 混沌方法，通過構造隨機基函數的同構酉變換，選取合適的投影空間，利用系統響應量在低維空間的結構逼近全系統，可在一定程度上緩解“維數災難”問題，提高計算效率，節約計算成本，在應用上具有可行性。例如，使用標準多元多項式混沌方法，展開5 次多項式，截斷長度為(14+5)!/14!5!-1=46 512-1=46 511，若使用基于自適應基函數的齊次Wiener混沌方法，截斷長度為(1+5)!/1!5!-1=5次，效率為 46 511/5 ≈104。

本文研究方法可用于指導船舶設計人員預測甲板上物體的振蕩范圍，判斷魚雷毀傷影響，為艦上人員采取防護措施提供建議，給出艦船加固標準，并判斷艦載設備裝艦的可行性。基于自適應基函數的齊次Wiener 混沌方法還可推廣到其他船舶沖擊響應研究中。

綜上所述，艦船非接觸水下爆炸的UQ 研究是一個系統工程，需要海洋、工程、數學、物理等各領域專家協同合作，本文僅給出了初步結果。下一步工作擬考慮以下問題：

1） 由于本文尚缺乏實驗數據與數值結果的比對，且尚未獲取真實的實驗數據，所以下一步擬與此領域的專家聯合研究水下爆炸試驗不確定度的傳播和量化，將實驗結果與數值結果進行比對，以確認模型的參數。

2） 本文未考慮模型不確定度的影響。事實上，炸藥類型不同，峰值壓力和衰減常數甚至是擬合函數公式也會不同，即使是同一類型的炸藥，也可能會用不同的經驗函數表示。因此，研究不同的經驗函數對系統輸出結果的影響，即模型形式不確定度 (model form uncertainty)的量化，將始終是UQ 研究的一個重要課題。

致謝

感謝山東科技大學公派訪問學者項目對第一作者在美國南加州大學訪學期間的資助。感謝南加州大學Roger Ghanem 教授對本文選題提出的建議。