納米微粒補強橡膠機理研究分析

劉 豐，李小紅

(1 洛陽師范學院化學化工學院，河南 洛陽 471934； 2 河南大學納米材料工程中心，河南 開封 475001)

橡膠以其優異獨特的性能，在生產生活中有著廣泛的應用。但是不經過補強的橡膠力學性能較差，幾乎沒有什么應用價值，因此橡膠的補強直接決定了橡膠的應用性能。橡膠的補強材料中，炭黑和納米二氧化硅微粒應用最為廣泛，人們對其補強機理的研究也較為充分。對納米微粒補強硅橡膠的機理的正確認識有助于我們更好地通過補強來調節硅橡膠的使用性能。

Payne效應的解釋是補強機理的一個重要方面。Payne效應指的是混煉橡膠橡膠材料，在較小交變應變下具有較大模量，而在較大的應變范圍內模量較小，材料的模量變化隨應變的改變有較大變化。本工作在已有研究結果[1-2]的基礎上，通過分析對比，在研究工作者已提出的補強機理基礎上，提出了新的解釋，該解釋更能充分解釋一些補強現象。

1 橡膠補強機理

眾所周知，橡膠補強能顯著改善材料的物理和機械性能，如提高材料的模量、撕裂強度、拉伸強度、耐磨性和耐疲勞性能等，這一切都是因為加入了補強材料。橡膠的補強開始是由炭黑補強來完成的，稱為“炭黑補強”或“炭補強”。對于補強機理。從20世紀50-70年代，就爭論不休，期間提出了很多暫時性的理論，討論了這么多年，對炭黑補強橡膠的機理認識依然不夠充分，因為這么多理論、觀點和模型都只能解釋炭黑補強的某一個或兩個現象，無法對補強出現的現象給出一個合理的解釋，定義一個完整的概念。

針對炭黑補強橡膠后材料模量的增加，很多工作者都給出了模量增加的描述，但是，隨著研究的深入，一些新現象的出現讓后來研究人員不得不根據具體的情況作出修正：

Smallwood最早借用Einstain的黏度方程來描述補強現象，即：

E=E1(1+2.5V)

Guth和Gold[3]考慮到填料濃度較高時顆粒之間的相互擾動，對以上公式作了改動：

E=E1(1+2.5V+14.1V2)

但是此公式對于那些顆粒較細的高效補強填料，所計算的數據就會比實驗值小，Guth考慮了粒子聚集體的影響，認為球形粒子會聚集成棒狀，提出：

E=E1(1+0.67εV+14.1V2)

鑒于炭黑聚集體對橡膠的包容效應，Medalia將上式中的V用有效體積分數Veff取代，得：

這么多的修正措施，其實還是很難解釋錯綜復雜的補強體系，有些學者[4]提出了一個解釋這些計算偏差的觀點，主要是這些偏差來自于補強體系內形成了補強顆粒連接成的一個三維網絡結構。還有學者[5]認為補強顆粒“三維”結構填充體系中形成了一種碳凝膠，就是很多橡膠分子鏈牢固地吸附在顆粒的表面，形成了“結合膠”，研究認為橡膠分子鏈只是包裹在顆粒的表面，結合膠的厚度只有2.0～7.5 nm，但是TEM觀察發現，實際的厚度能達到25～30 nm，很多工作研究表明，如果炭黑的添加量是30 phr，整個橡膠體系中結合膠能占50%，如果添加量為50 phr，結合膠所占的比例能達到50%～70%。

納米微粒的“三維”結構普遍被接受并用來解釋補強現象，有學者認為“三維”結構是由于表面能比較高的納米粒子間相互作用產生的[6],也有人認為是表面帶有“結合膠”的復合微粒由于表面的橡膠分子鏈互相纏結形成的網絡結構。補強后的復合材料在收到應力時，“三維”網絡結構由于具有較大的強度，能較為有效地傳遞應力，并且在材料形變時，網絡結構的變形能消耗很多能量，表現出較大的強度。納米補強微粒即使不能實現單個顆粒均勻分散，但是依靠顆粒間的鏈接，以及顆粒鏈或網絡表面上的結合膠能大大加快應力傳遞。

前期工作中[1-2]，研究采用不同表面處理的納米微粒來補強硅橡膠，研究發現，補強效果的強弱與顆粒的分散程度，顆粒與橡膠基體間的界面強度有關。研究認為表面原位修飾的納米微粒在硅橡膠中分散更為均勻，無機-有機接觸面積更大，產生的結合膠數量也越多。這使得材料在較小形變時具有較大的模量，由于材料分布均勻，應力集中現象很少，能產生較大的形變，而在較大形變時，模量減小。這是因為結合膠是一種類似玻璃態的橡膠形態，低應變時，結合膠模量較大是補強的主要原因之一，在高應變時，結合膠處的分子鏈收到較大應力產生屈服開始形變，而結合膠內部的交聯點是比較少的，屈服的橡膠分子在相同應力下能產生較大的形變，故而此時模量較小；隨著形變繼續增加，結合膠中分子都沿著應力方向發生取向，更大的形變需要分子鏈的斷裂或與補強顆粒脫離，這需要更大的外力，材料模量又持續變大，補強示意圖如圖1所示。

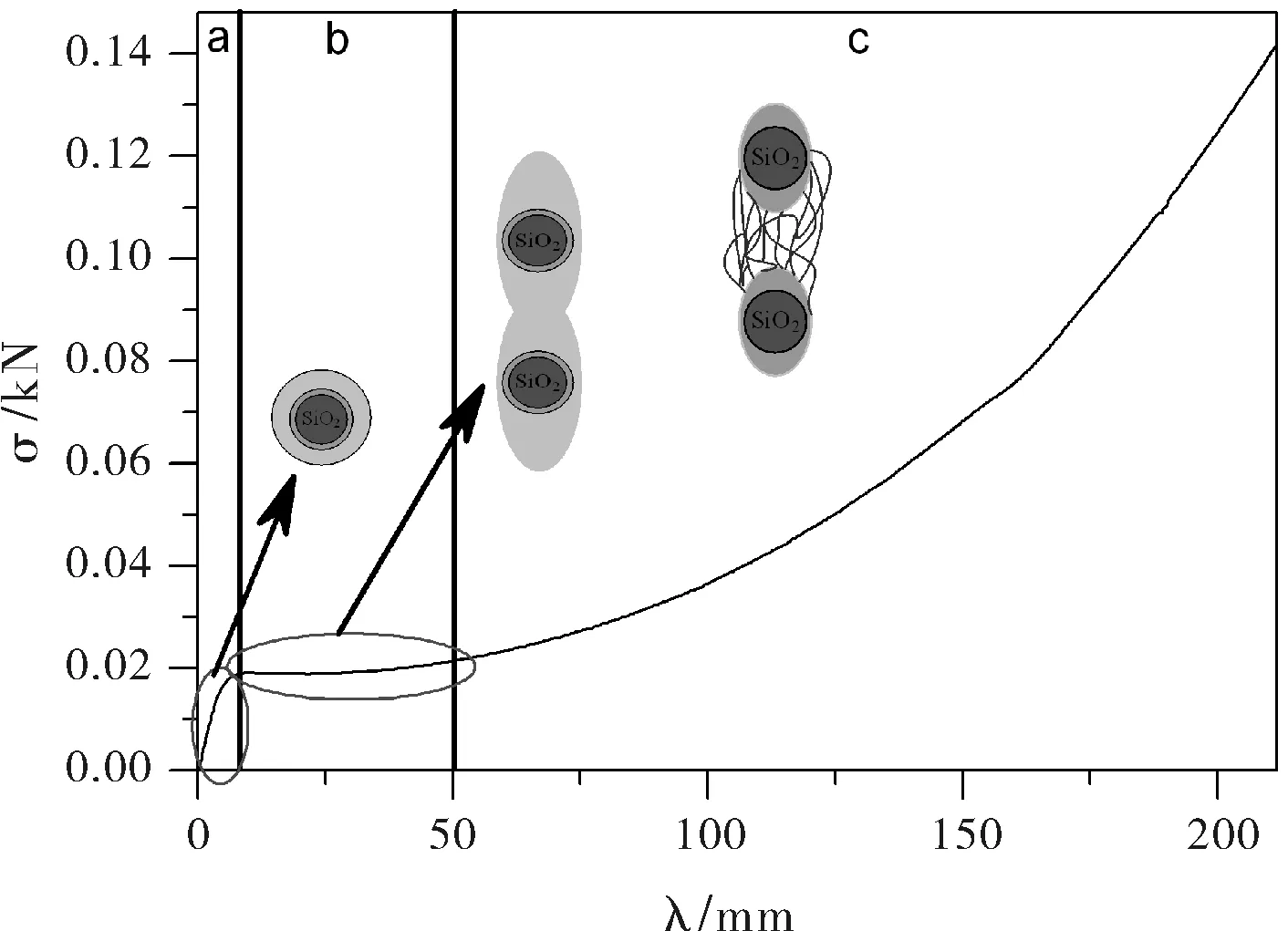
圖1 填充橡膠內部微觀結構結構隨應變變化示意圖

這種補強機理的闡述能解釋很多解釋不同的現象，比如補強橡膠的應力應變曲線開始斜率大，中等應變時模量減小，高形變是模量又迅速增大。如果能使中等形變的模量增大，則能更好地補強橡膠，體現在200%和300%的定伸應力的提高。我們采用表面帶有可反應性官能團的納米二氧化硅補強硅橡膠，可反應性官能團能在硫化時在結合膠內部產生更多的化學交聯點，這樣在中等應變時，結合膠在受力發生屈服產生取向時，需要克服更大的阻力，表現出較高的模量。

2 Payne效應的解釋

動態模量的下降是由于填料間的物理作用力的破壞，而能量耗散的增加則是由于聚集體的不斷的破壞和重組造成的。后來，許多學者在構建網絡模型時，都延續這種觀點，只是他們模型中所采用的結構單元彼此不同，所用的數學推導的方式不同。但是不管怎么樣，我們可以從Payne效應得出一個很重要的結論：材料的動態模量隨著應變的增加而下降，肯定是由于其中的某種或者某些網絡結構遭到了破壞；在動態應變過程中，能量的耗散的增加，也主要是由于網絡結構的破壞重組而造成的。而這些網絡結構，也只是各種不同模型的區別點。至今，已經有很多的學者，提出各種各樣的模型試圖解釋Payne效應的本質。但是這些模型的都具有一定的局限性，大致分為兩類觀點：一是認為Payne效應的主要原因是由于填料或者填料聚集體之間的相互作用形成的填料網絡遭到破壞；另外一類則認為，填料和基體之間各種相互作用是控制Payne效應根本因素。

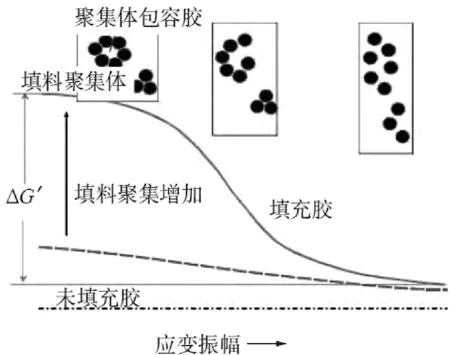
圖2 Payne 效應示意圖[7]

王夢蛟[6]認為，在填充橡膠硫化體系中，當體系承受較小應變時，體系中的應力承受者是那些高模量的網絡結構，由于應變小，網絡結構不會被破壞，并且網絡結構傳遞應力的效率是很高的，表現形式是模量較大；隨著應變的增大，逐漸接近一個應變范圍，在給定的的振動頻率條件下，這些網絡結構就會遭到破壞，但是同時還會自動恢復，網絡結構的破壞，大大降低了外力的傳遞效率，此時模量迅速下降，但是這個階段的網絡結構的破壞也伴隨著結構的重整，需要消耗大量的能量，此時必然伴隨著損耗模量的增大，而此階段的損耗模量也確實如此；應變繼續增大，如果振動頻率不延長的話，在這樣短的周期內，網絡結構就不會再自動恢復了，此時補強體系賴以有效傳遞應力的介質徹底被瓦解了，表現形式是儲能模量迅速降低到最低點，降低到沒有補強體系的動態儲能模量，不管補強體系所填充的補強顆粒什么樣的性質，最后都歸于橡膠基體最基本的動態儲能模量，其示意圖如圖2所示。

通過研究發現，以往Payne效應的闡述并不能解釋一些細節問題，比如：應變頻率一直是不變的，而且在相同添加量的情況下，即使在高應變情況下，顆粒間的平均距離也不會增大，如果小應變能實現填料網絡的重構，大應變也應該能，但是為什么在大應變是動態模量迅速減小到未填充膠模量大小。如果用結合膠的結構和相互間的作用方式來解釋就能解釋上述問題。

核磁研究了結合膠的結構，認為結合膠至少可以分為兩層：與炭黑顆粒表面直接接觸的的一層橡膠分子鏈被牢牢地固定在顆粒的表面，分子很難運動，處于玻璃態，另一層則是處于玻璃態橡膠分子鏈延伸出來的，雖然可以活動一些，但相對于沒有補強的橡膠體系，這些分子鏈的運動還是受限制的，如圖2所示。很多文獻表明，補強材料添加量越大，Payne效應

就越明顯。據此，可以把整個混煉膠體系看做是由表面帶有結合膠的復合微粒和自由橡膠分子鏈組成。結合膠含量越多，自由分子鏈就越少，每個復合顆粒外層有運動能力的分子間的糾纏就越多，材料整體強度就越大，在小形變時，橡膠分子鏈的糾纏不會減少，或減少不多；當形變較大時顆粒間的相對位移較大，發生了解糾纏，整個材料間的相互作用力就減小了很多，動態模量迅速下降直至最低與未填充膠的模量一樣小，因為此時，材料內部的相互作用就是分子鏈間的相互作用。

3 結 語

橡膠的補強是因為由于處于玻璃態的結合膠的存在，使得材料在發生較小形變時，結合膠不發生形變，那橡膠基體材料的形變就會發生放大效應，也就是說少量的基體材料承擔了材料的整個形變，表現出了較大的模量；隨著形變的增加，結合膠所受的應力增大，一直到發生屈服，并在一定的應力作用下發生了較大的取向形變，模量表現較小；當形變繼續增加，發生取向的分子鏈不容易繼續形變，但能承擔更高的應力，模量表現較大。

Payne效應的發生的機理同樣是由于大量結合膠的存在，復合顆粒間的相互作用為糾纏的分子鏈；相同應變頻率下，小形變不會或很少減少這種相互作用，動態模量表現較大；形變較大時，復合顆粒相對位移較大，顆粒間發生了分子鏈的解糾纏，材料內部的相互作用力與為補強膠一樣，是分子鏈間的相互作用，模量較小。表現出隨著應變的增加，混煉膠的動態模量大幅度較小的Payne效應。