無源無線應變傳感器的模擬與測試

薛松濤 徐康乾 謝麗宇，* 薛 科 萬國春

（1.同濟大學結構防災減災工程系，上海200092；2.日本東北工業大學工學部建筑學科，日本仙臺；3.同濟大學電子與信息工程學院，上海201804）

0 引 言

在使用荷載以及環境作用下建筑結構的性能會逐漸發生退化，因此結構健康監測在近幾十年來得到了廣泛的發展，用于監測和評估結構的狀態［1］。

在結構健康監測中，應變監測是一個重要的內容，通過監測應變判斷結構構件的受力狀態，為結構評估提供合理的依據。應變監測中常用的傳統應變傳感器有電阻應變傳感器［2］、光纖光柵傳感器［3］和弦振式應變傳感器［4］等。這些傳統的傳感器性能可靠，使用方便，但是需導線為傳感器提供電源以及進行數據傳輸。當大范圍布置傳感器時，大量的導線使傳感系統變得冗雜，并且在災害發生時容易損壞致使傳感系統不能正常工作。

土木工程有其自身的特點，對傳感器有著與其他領域的不同要求，需要針對土木工程的特有環境開發出滿足需要的傳感器［5］。將健康監測系統應用在大規模的土木工程，為了監測局部的物理量，需要大量的傳感器，形成具有分布式傳感器的監測系統（distributed sensor-based SHM），要求傳感器造價低、可靠性好，這樣才可以提高傳感器空間分布的密度［6］（spatial granularity）。因此，需要尋找一種無須能源供應、可無線傳輸、耐久性好且價格低廉的傳感器，用于結構局部損傷的監測。RFID（Radio Frequency Identification）即射頻識別技術可滿足這些要求［7-8］，為大規模分布式傳感器監測系統的應用提供了可能［9］。

在RFID 系統中，天線起著重要的作用，它是接收和輻射電磁波的裝置，必須具有合適的形狀、結構和饋電方式。隨著進一步的研究，學者們發現天線經歷應變時，天線的電學性質（如諧振頻率）發生改變，因此天線可同時作為應變傳感單元和信息傳輸單元，實現傳感的無源和無線。Yi等［10，11］開發了一種矩形貼片天線傳感器用以檢測應變，貼片天線頻帶較窄，諧振頻率易于提取。2017年，薛松濤等［12］提出了一種不帶芯片的矩形貼片天線應變傳感器，天線的工作頻段為2.45 GHz，通過數值模擬和試驗證實了貼片天線可作為可靠的應變感應單元，具有良好的線性，精度可達萬分之一個應變，但其傳輸方式仍采用了同軸線。本文在該研究的基礎上，增加了芯片，重新設計了電路［13］，實現了貼片天線應變傳感器的無源和無線。

本文設計了一種工作頻率為920 MHz的四分之一矩形貼片天線應變傳感器。相比于傳統電阻應變傳感器，天線傳感器的厚度尺寸較大，這導致因剪力滯后效應引起的傳遞效率將不可忽略。本文將采用數值模擬和試驗的方法驗證該現象并確定傳遞效率系數，結合理論推導進而給出傳感器靈敏度系數的計算公式。最后設計拉伸試驗將傳感器靈敏度系數的計算值與實測值相對比，驗證天線傳感器檢測應變性能的可靠性。

1 RFID應變傳感系統

RFID 是一種利用射頻通信實現的非接觸式自動識別技術，按照是否需要外部供電分為有源和無源（Passive）兩種。如圖1（a）所示，基于RFID技術的無源無線應變傳感系統由RFID 閱讀器和RFID 天線傳感器組成。天線傳感器（圖1（b））包括貼片天線和IC 芯片兩部分。其中，貼片天線為應變感應和信息傳輸單元，由基板、上輻射貼片、下輻射貼片、過孔和匹配線構成；IC 芯片為回路的負載，可存儲位置等信息。

圖1 RFID應變傳感器系統Fig.1 RFID Strain sensing system

天線傳感器與閱讀器通過電磁波完成能量的傳遞以及信息的傳輸。天線傳感器接受電磁波后貼片天線產生電流與負載形成回路，其中在貼片天線中電流的方向即為傳感器的長度方向，如圖1所示。

該應變傳感器是根據貼片天線的諧振頻率檢測應變。諧振頻率是天線的最佳工作頻率，即在此頻率下RFID 系統的功率傳輸達到最大化。接下來，第1.1 節將討論如何進行貼片天線的設計；第1.2節將對天線的諧振頻率與應變的關系進行理論推導；第1.3節將介紹試驗中諧振頻率測量的原理與方法。

1.1 RFID天線設計

對于四分之一波長的矩形貼片天線，其初始諧振頻率由下式近似計算［14］：

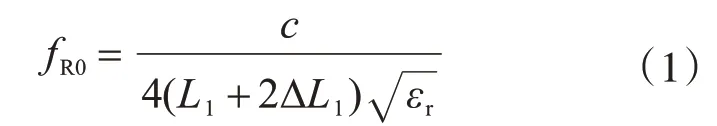
式中：fR0為初始諧振頻率；c為真空中光速；L1為上輻射貼片的長度；εr為基板的相對介電常數；ΔL1為考慮介質板效應的補償介電長度。

依據式（1）對貼片天線進行設計，基板材料選用RT/duroid?5880，相對介電常數為2.2，尺寸選為69 mm×61 mm×0.5 mm，上輻射貼片和下輻射貼片均為鍍銅層，上輻射貼片尺寸選為54.9 mm×50 mm×0.1 mm，下輻射貼片尺寸為69 mm×61 mm×0.1 mm，與基板平面尺寸相同。天線具體尺寸見圖2與表1，將尺寸參數帶入式（1），計算得天線初始諧振頻率為918.10 MHz。

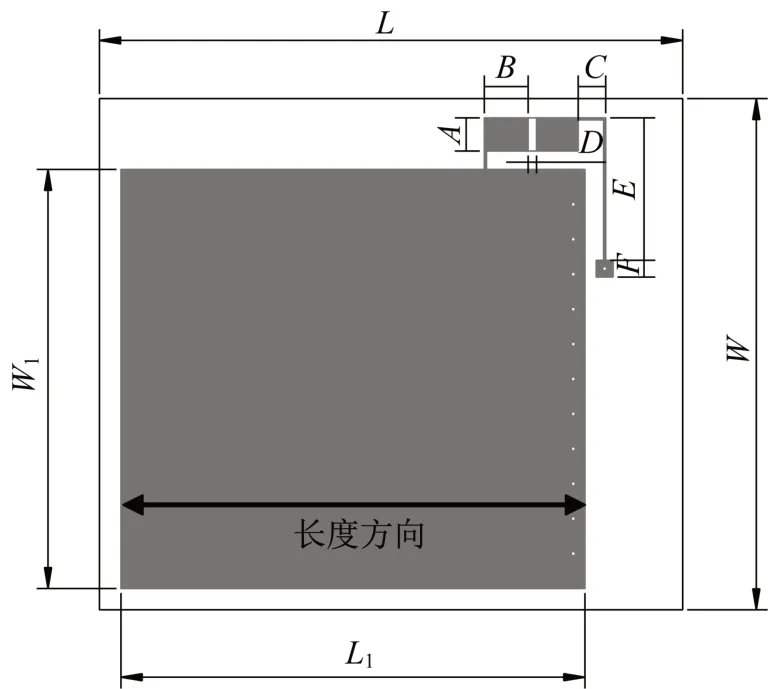
圖2 天線尺寸參數Fig.2 Dimensions of antenna

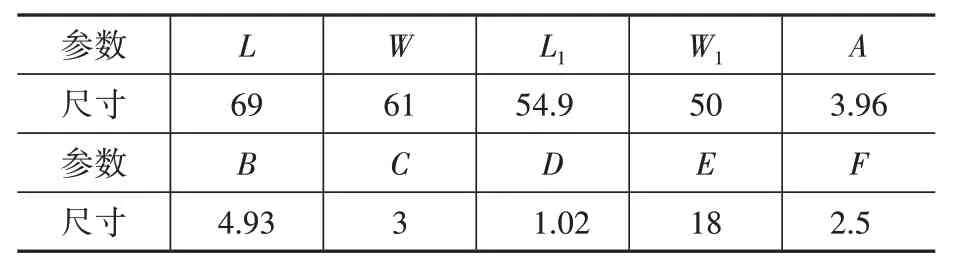
表1 天線具體尺寸Table 1 Antenna specific dimensions mm

1.2 應變測量的原理

根據式（1）可知，天線諧振頻率fR受上輻射貼片的長度L1和補償介電長度ΔL1的影響。一般L1》ΔL1，若忽略ΔL1的影響，當貼片天線在長度方向經歷應變ε時，上輻射貼片的長度將變為L1(1+ε)，代入式（1）可得對應的諧振頻率fR：

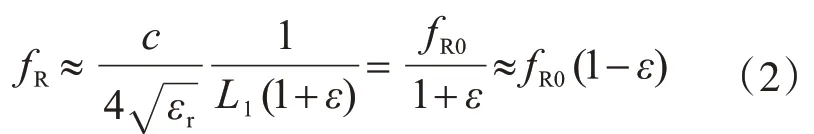
可發現貼片天線的諧振頻率fR與其長度方向的應變簡化為近似的線性關系，斜率的絕對值為初始諧振頻率fR0。也即天線的長度方向為傳感器的應變感應方向，而因泊松效應引起寬度方向的變形對諧振頻率的影響可忽略。因此，通過測量天線的諧振頻率變化可推算出天線長度方向所經歷的應變變化。

1.3 天線諧振頻率的測量

如圖1（a）所示，假定閱讀器與天線之間無障礙物，由Friis 自由空間公式可得天線的接收功率P2［15］：

式中：P1為閱讀器發射功率；G1為閱讀器天線增益；G2為貼片天線增益，λ為閱讀器所發射電磁波的波長；d為閱讀器與貼片天線之間的距離；f為閱讀器所發射電磁波的頻率，即天線的工作頻率。

天線接收來自于閱讀器的功率并向負載傳輸，其中一部分功率被反射而不能被利用，定義反射系數η(f)為

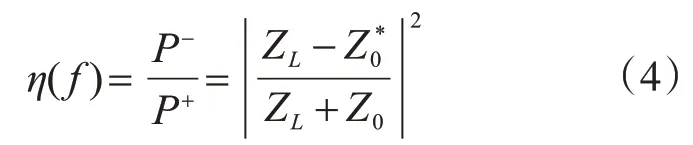
式中：P-為反射功率；P+為輸入功率；ZL為負載阻抗；Z0為貼片天線的特性阻抗；Z*0為貼片天線特性阻抗的共軛，其均為天線工作頻率的函數。當天線的工作頻率等于諧振頻率時，天線與芯片的阻抗最佳匹配，η(f)取得最小值，即諧振頻率是天線的最佳工作頻率。

通過反射系數可得芯片所接收的功率P3為

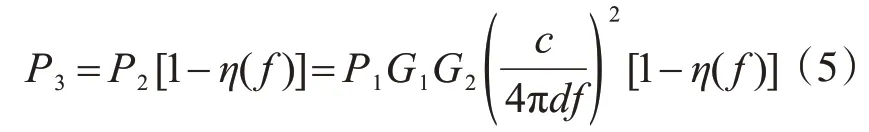
功率由芯片再次返回貼片天線時，同樣有一部分功率被反射，反射系數同式（4），所返回的功率P2'為

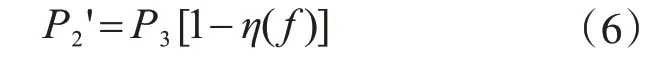
此時貼片天線作為一個功率為P2'的發射源發射電磁波，類比式（3），閱讀器天線接收到的功率即反射功率P1'為

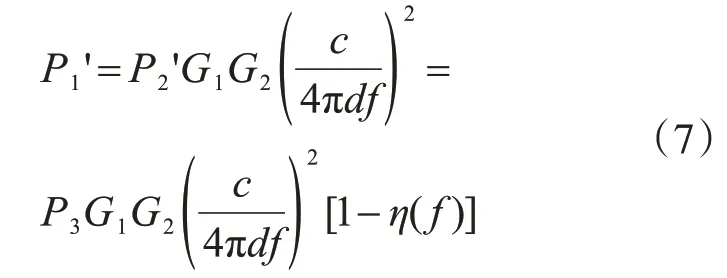
芯片作為一個負載，正常工作所需的最小激活功率為PIC，其不隨天線工作頻率f改變。在某一頻率f下，當芯片恰好被激活時，芯片的接收功率為

將式（8）帶入式（5），可得該頻率f下的閾值發射功率P1S：

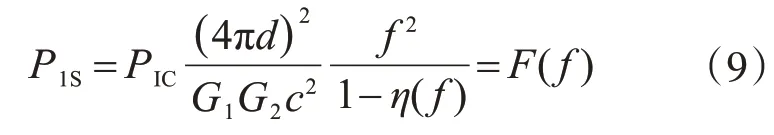
將式（8）帶入式（7），對應的閾值反射功率P1S'為

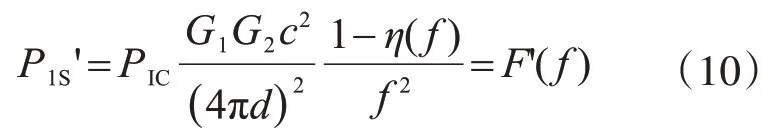
閱讀器天線和貼片天線的增益G1和G2均為一常數，其間距固定時d也為定值。當閱讀器所發射電磁波的頻率f改變時，根據函數η(f)的特性可知，函數F(f)有最小值，函數F'(f)有最大值，即在某一頻率范圍內閾值發射功率最小值點和閾值反射功率最大值點對應的頻率為天線的諧振頻率（圖3）。因此，可根據采集的閾值發射功率曲線和閾值反射功率曲線確定天線的諧振頻率。

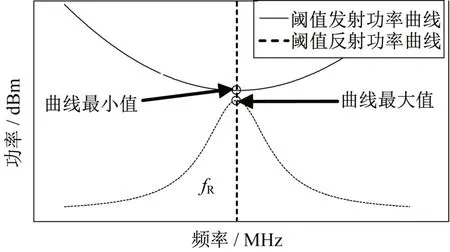
圖3 閾值功率曲線示意圖Fig.3 Threshold power curves

2 應變傳遞效率驗證

通過強力膠將RFID天線粘貼在試件表面，進行試件的拉伸試驗，由于存在剪力滯后效應，天線上輻射貼片的應變不會達到試件表面應變的大小。本節通過數值模擬及拉伸試驗對剪力滯后效應進行驗證，并根據試驗結果計算應變的傳遞效率系數。試件單向拉伸時的拉伸方向定義為縱向，垂直于拉伸的方向為橫向，在復雜應力狀態下兩個主應變方向分別定義為縱向和橫向。則縱向傳遞效率系數η可按下式計算：

式中：εc為上輻射貼片的縱向應變；εs為試件的縱向應變。

橫向傳遞效率系數η'的定義類比式（11），為上輻射貼片與試件橫向應變的比值。但若天線的主要部件基板與試件的泊松比不同，則會引起縱向傳遞效率系數與橫向傳遞效率系數的差異。

選用鋁板作為拉伸試件，由于所用夾具（WDW-50，濟南測試廠）的限制，端部尺寸不得超過3 cm，而粘貼天線的區域不得小于天線最大尺寸6.9 cm，故本試驗所用試件模型如圖4 所示。其中區域I 為加載區域，區域II 為力傳遞區域，區域III 為傳感器粘貼區域。經過傳遞區域可保證中間傳感器粘貼區域所受到的拉應力均勻分布。

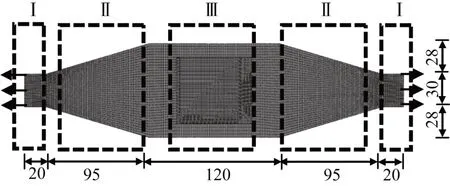
圖4 有限元模型（單位：mm）Fig.4 The finite element model（Unit：mm）

2.1 數值模擬

采用ABAQUS 軟件建立有限元模型，其中鋁板和基板采用實體單元，上、下輻射貼片采用殼單元，各部件厚度及材料參數如表2 所示。模型中不考慮膠水的影響，即假定天線與鋁板之間界面的變形是連續的，沒有應變的損失。

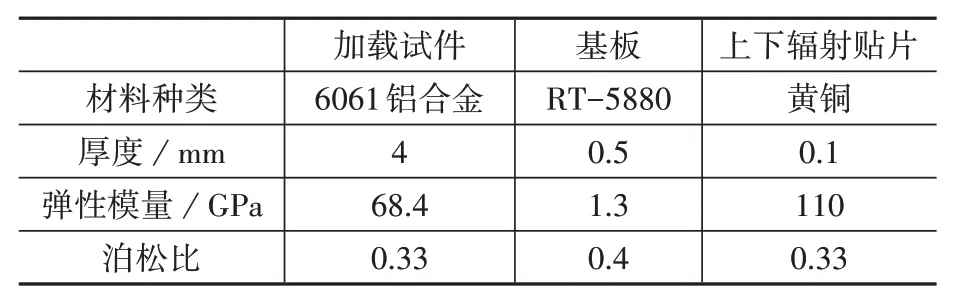
表2 材料參數Table 2 Material parameters

劃分網格時，考慮到天線邊緣應變變化可能較大，所以網格劃分較細密，以保證計算精度；鋁板的力傳遞區域由于拐角的存在會產生應力集中，但不是本文所研究的重點，所以網格劃分相對稀疏，以提高計算效率。劃分網格之后的ABAQUS有限元模型平面圖如圖4所示。

在3 kN 荷載作用下，粘貼天線的試件與未粘貼天線試件的縱向應變云圖如圖5 所示。可見兩試件應變云圖基本一致，即粘貼天線后對鋁板應變的影響可忽略，所以鋁板的縱向平均應變可通過公式近似計算得到，此時平均應變為127.5με。

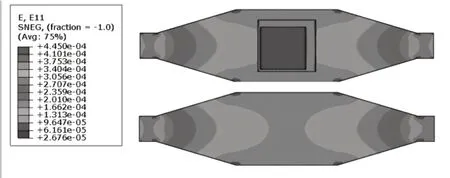
圖5 有無天線時的縱向應變云圖Fig.5 Strain contour with and without antenna

天線及附近鋁板的應變云圖與天線上貼片天線的應變云圖如圖6 所示。在上輻射貼片的邊界區域，應變值由鋁板的平均應變127.5με快速衰減至 90.6～96.4με之間，如圖6（b）所示。提取上輻射貼片的平均應變為94.5με，計算得縱向應變傳遞效率系數為74.12%。

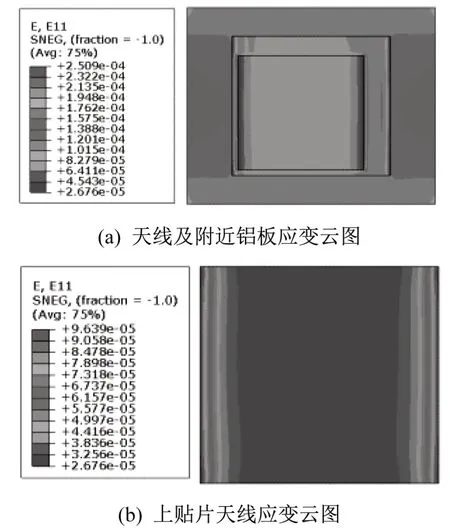
圖6 局部應變云圖Fig.6 Local strain contour

在此荷載作用下提取鋁板橫向平均應變為42.2με，與鋁板縱向平均應變比值為0.331，接近鋁材泊松比；提取上輻射貼片橫向平均應變為37.5με，與上輻射貼片縱向平均應變比值為0.397，接近基板泊松比。因此，可知縱向傳遞效率系數與橫向傳遞效率系數之比約為鋁板與天線基板泊松比之比：

式中：vA為鋁板泊松比；vS為基板泊松比。

2.2 傳遞效率試驗

通過強力膠將RFID天線粘貼在試件表面，并在上輻射貼片表面和試件表面粘貼應變片，進行試件拉伸試驗，驗證應變的傳遞效率。試樣如圖7（a）所示，應變片①和②粘貼在上輻射貼片表面，應變片③和④粘貼在鋁板表面。其中應變片①和③的應變感應方向與拉伸方向平行，應變片②和④的應變感應方向與拉伸方向垂直。拉伸機型號為SJV-30000，拉伸裝置如圖7（b）所示，應變采集儀選用LC1007。試驗采用分級加載，以3kN 為一級，加載至24 kN共八級，總共拉伸3個試樣，所得荷載-應變圖如圖8所示。

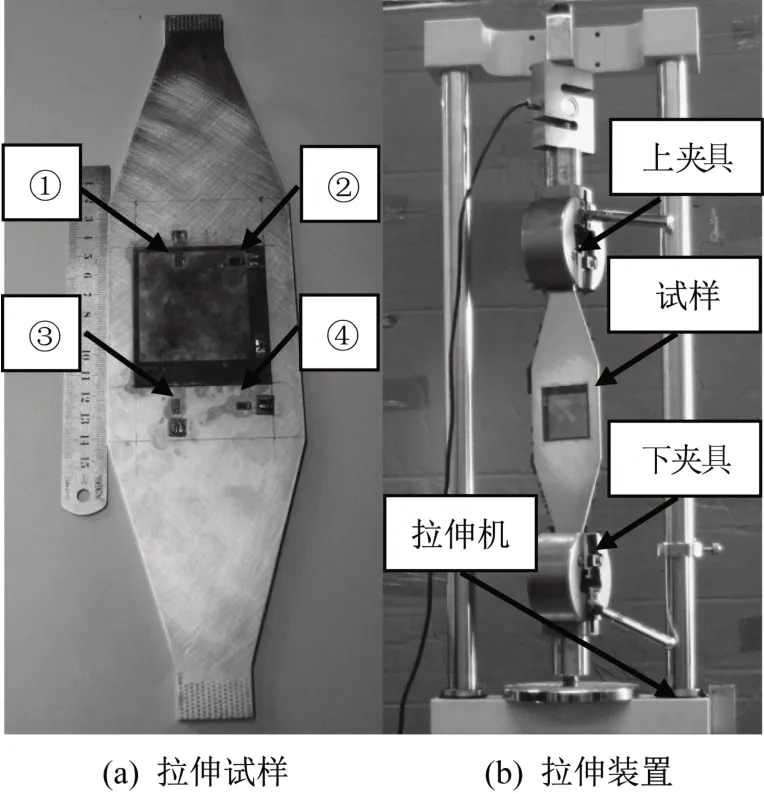
圖7 傳遞效率試驗Fig.7 Transfer efficiency experiment

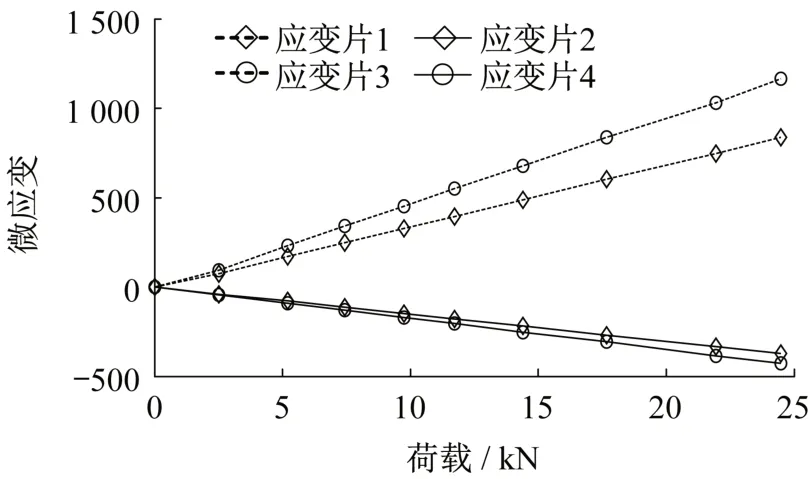
圖8 荷載-應變曲線圖Fig.8 Load-strain curve

應變片①與③的應變比值為縱向傳遞效率系數，應變片②與④的應變比值為橫向傳遞效率系數，計算結果如表3 所示。將橫向傳遞效率系數平均值代入式（12）換算為縱向傳遞效率系數，其值為73.54%，與直接所得的縱向傳遞效率系數74.23%的相對誤差僅為0.93%，非常接近。因此取二者平均值73.88%作為縱向傳遞效率系數的試驗值，與數值模擬所得傳縱向遞效率系數74.12%的相對誤差為0.3%，兩者符合較好。

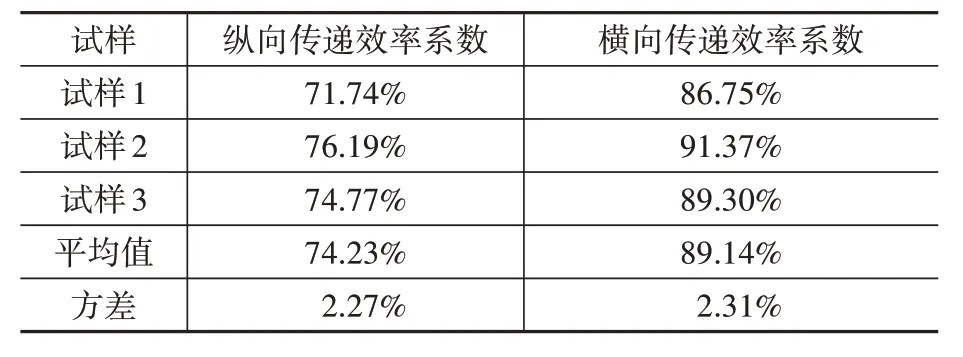
表3 傳遞效率試驗結果Table 3 Experimental results of transfer efficiency

2.3 靈敏度系數

試件在傳感器應變感應方向的單位應變所引起天線諧振頻率的改變量為天線應變傳感器的靈敏度，結合章節1.2推導可得靈敏度系數R：

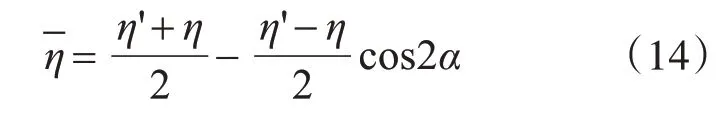
夾角α的取值介于0～90°之間。若為復雜應力狀態，則α應為應變感應方向與主應變方向的夾角。

3 天線傳感器的測試

當天線傳感器的應變與諧振頻率有著較好的線性關系時，靈敏度系數的精確性便直接決定了應變檢測的準確性。因此，本節采用數值模擬和拉伸試驗的方法，探究RFID天線傳感器經歷應變時諧振頻率與應變的線性度以及傳感器靈敏度系數的精確度。

其中，數值模擬直接控制天線的應變，此時不需考慮傳遞效率，所擬合直線的斜率即為傳感器的靈敏度系數，根據理論推導直接將其與天線的初始諧振頻率進行比較，驗證與理論值的符合程度。

設計拉伸試驗時，考慮傳感器的應變感應方向與拉伸方向平行和垂直的兩種情況。試驗所得應變-諧振頻率擬合直線的斜率即為實測靈敏度系數，將其分別與經式（13）所得計算靈敏度系數相對比，驗證傳遞效率對靈敏度系數的影響。

3.1 數值模擬

在HFSSTM中建立模型，假設天線發生均勻變形，通過改變天線尺寸L、W、L1以及W1等相關參數的方法模擬天線應變［16］，此時不需考慮應變傳遞效率的影響。由于軟件求解精度的限制，若相鄰兩級的應變增量較小可能會出現較大誤差。故在數值模擬中，天線應變以2 000με為一級，加載至10 000με，所得的回波損耗曲線如圖9所示，其中回波損耗系數S11定義為

由1.3節中函數η(f)的性質可知，當回波損耗曲線取得最小值時的工作頻率為天線的諧振頻率。依此提取各級應變下的諧振頻率，繪制應變-諧振頻率關系曲線，如圖10 所示。所得天線初始諧振頻率的模擬值為917.88 MHz，與章節1.1 中式（1）的計算值918.10M Hz的相對誤差為0.02%，結果十分一致。擬合直線的相關系數為0.999 1，說明天線的諧振頻率與應變具有較好的線性關系；擬合直線的斜率為-915.43 MHz·ε-1，表示每單位應變使諧振頻率產生915.43 MHz 的漂移量。其絕對值與初始諧振頻率模擬值的相對誤差為0.27%，符合式（2）的理論推導。在實際測量中當采樣頻率小于所測應變對應的諧振頻率漂移量時，將不會對測試結果造成過大的影響。

3.2 拉伸試驗

為減少環境干擾，拉伸試驗在微波暗室里進行，試驗裝置如圖11 所示。閱讀器固定在三腳架上，與貼片天線之間的距離為0.4 m。

試驗中RFID 閱讀器選用Tagformance Pro，可檢測工作在超高頻段天線的閾值發射功率曲線和閾值反射功率曲線，其所采集的功率為對數功率（單位：dBm），與式（9）和式（10）計算所得功率P（單位：W）的換算關系為

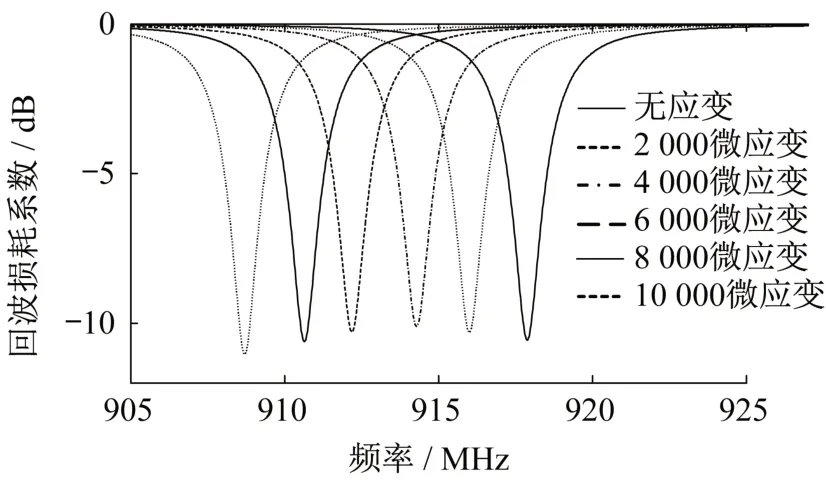
圖9 諧振頻率偏移曲線Fig.9 Curves of resonant frequency shift

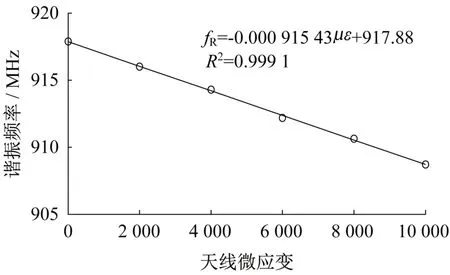
圖10 應變-諧振頻率擬合直線Fig.10 Fitted line of strain and resonant frequency

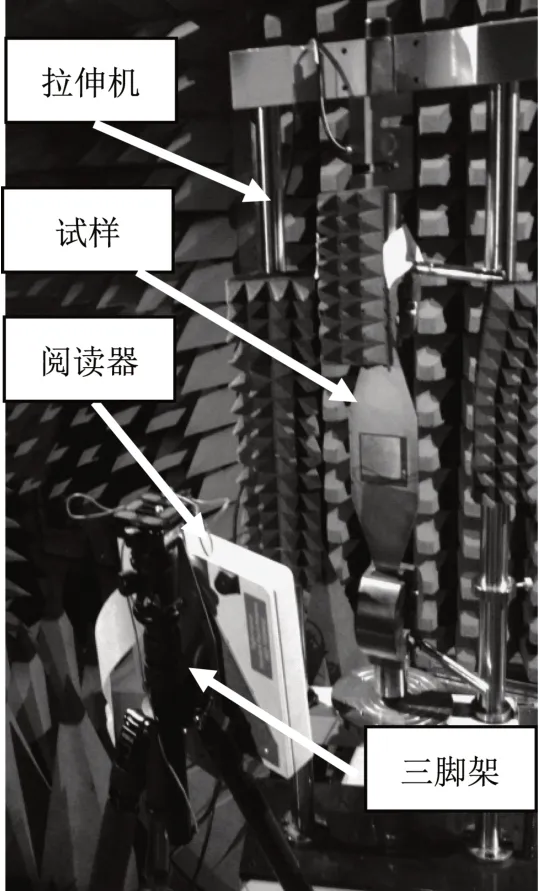
圖11 試驗裝置Fig.11 Experiment setup

試驗所用鋁板尺寸如圖4 所示，采用拉伸機（SJV-30000）對試樣分級加載，3 kN為一級共加載8級，與傳遞效率試驗相同。

為探究不同情況下經式（13）所得計算靈敏度系數與實測靈敏度系數的相符程度，將RFID天線傳感器粘貼在鋁板表面進行拉伸，方案一使天線長度方向與拉伸方向平行，即縱向粘貼，試樣如圖12（a）所示；方案二使天線長度方向與拉伸方向垂直，即橫向粘貼，試樣如圖12（b）所示。

圖12 天線鋁板試樣Fig.12 Experiment sample

3.3 結果分析

為減小試驗誤差，每級荷載下分別記錄五組數據，其中每組數據包括頻率-閾值發射功率曲線和頻率-閾值反射功率曲線，分別按式（17）取平均值，所得曲線如圖13 所示。可見頻率-發射功率曲線波谷相對較平緩，提取最小值時容易引起較大的誤差，所以本文中采用頻率-反射功率曲線提取諧振頻率，以提高精度。

為進一步減小環境噪聲的影響，選取頻率-反射功率曲線最大值附近的局部曲線，采用四次多項式進行擬合，取局部擬合曲線的最大值點作為天線在該級應變下的諧振頻率點，如圖14（a）所示。某一試樣在無荷載、12 kN 和24 kN 荷載作用下的局部頻率-反射功率擬合曲線如圖14（b）所示，可見曲線隨荷載的增加向著諧振頻率減小的方向漂移，與數值模擬的規律一致。提取每級應變下貼片天線的諧振頻率，由于加工誤差的存在，不同貼片天線初始諧振頻率的試驗值不相同。為了方便對比，選用諧振頻率漂移量作為縱坐標，分別進行應變-諧振頻率漂移量的直線擬合，結果如圖15所示。

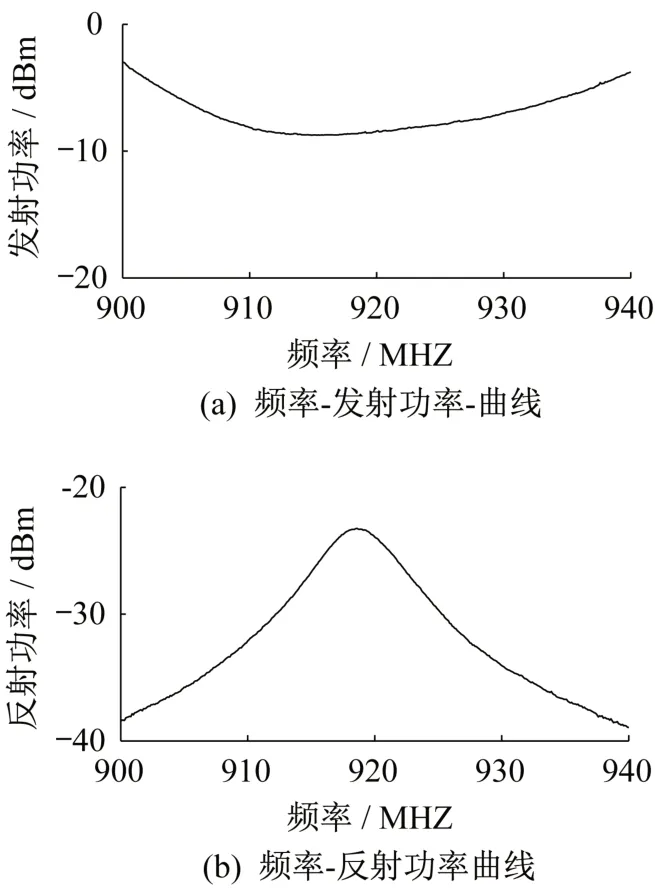
圖13 采集數據曲線圖Fig.13 Collected data curves

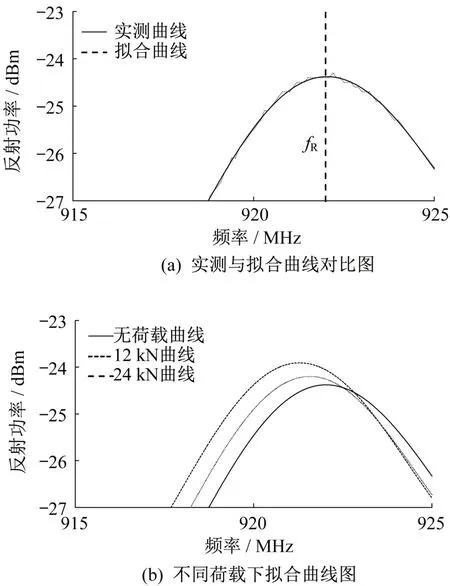
圖14 諧振頻率的處理及對比Fig.14 The processing and comparison of resonant frequency

對于縱向和橫向粘貼的天線，其初始諧振頻率與實測靈敏度系數如表4 所示，并根據式（13）得出計算靈敏度系數，其中天線傳感器縱向粘貼時傳遞效率系數取為第2 章節試驗結果的平均值73.88%，天線橫向粘貼時傳遞效率系數按式（12）取為73.88×0.4÷0.33=89.55%。

表4 天線初始諧振頻率與靈敏度Table 4 The initial resonant frequency and sensitivity

由表4 可見，兩組試驗所得靈敏度系數的計算值與實測值相對誤差的偏差較大，主要是因為采用強力膠粘接天線和試件，而天線的粘接底面積較大，涂膠不均勻會導致局部粘接不牢靠，引起傳遞效率的偏差。但縱向粘貼和橫向粘貼時平均相對誤差分別為3.98%和3.52%，均小于5%，滿足工程需求。這表明當天線傳感器的應變感應方向與拉伸方向平行或存在夾角時均可較準確地檢測試件在該方向上的應變。

當天線縱向粘貼時所擬合直線的相關系數接近于1，說明天線諧振頻率與應變有著較好的線性關系，與理論推導和數值模擬結論一致。當天線橫向粘貼時擬合直線的線性度稍差一些，主要是由于橫向粘貼時應變步長以及對應的諧振頻率漂移量僅為原先的0.33 倍，在同樣的諧振頻率測量誤差下也會引起擬合直線線性度的降低。因此減小諧振頻率的測量誤差以提高該傳感器的測量精度也較為重要。

4 結 論

本文基于射頻識別技術設計了帶芯片的貼片天線傳感器，實現了應變傳感器的無源無線。通過數值模擬和拉伸試驗對粘貼在試件上的天線所存在的剪力滯后現象進行了驗證，且所得傳遞效率系數二者相符較好，并依此給出了天線傳感器靈敏度系數的計算方法。然后通過模擬和試驗對天線進行拉伸，驗證了應變與諧振頻率的線性關系，且在傳感器的感應方向與拉伸方向平行和垂直的兩種情況下，實測靈敏度系數與計算靈敏度系數的相對誤差均小于5%，試驗結果表明該應變傳感器可準確檢測萬分之一量級應變的傳感器。

基于貼片天線的特性可知，當天線尺寸不發生變動時其諧振頻率的漂移量可以忽略，但當溫度改變時會對諧振頻率產生影響，下一步將會對溫度補償展開研究。此外，由于該傳感器較電阻應變傳感器具有較大的尺寸，因此其適用于表面平坦且應力變化較小的結構構件處，未來也將會對此傳感器進行小型化的研究。