混合梁剛構橋體外預應力鋼束設置與優化

林志平

（福建省高速公路集團有限公司，福州350001）

0 引 言

混合梁剛構橋是在主跨跨中處采用一段鋼梁代替混凝土梁，能夠有效增大傳統混凝土剛構橋的跨徑，并在一定程度上緩解其跨中梁體易開裂與跨中撓度過大等問題［1-2］。目前，混合梁剛構橋在國內的應用仍處于發展階段，工程實例較少，已建成通車的僅有重慶石板坡長江大橋復線橋、溫州甌江大橋、中山小欖水道大橋、舟山魚山大橋等，在建的福建泉州安海灣大橋預計2020年12月建成通車。

在大跨徑預應力混凝土剛構橋中，為了減小混凝土拉應力，增大橋梁跨徑，需要配置一定數量的預應力鋼束，包括頂板鋼束、底板鋼束和腹板鋼束等大量體內預應力鋼束［3］。隨著體外預應力技術的發展，體內外混合配束成為大跨徑混凝土連續剛構橋的主流配束方式，它的最大優點在于體外預應力便于后期補張與更換，從而能提供更為可靠的豎向和縱向預應力，有效抑制混凝土腹板的開裂和跨中下撓［4］。馬振棟等研究發現體外預應力能夠有效控制大跨徑連續剛構橋的跨中撓度［5］。徐棟等分析了體外預應力在大跨徑連續剛構橋抗剪設計中所發揮的作用［6］。艾軍等介紹了利用體外預應力對公路橋梁進行加固設計的方法［7］。皮薩尼研究了設置體外預應力的混凝土梁在長期效應作用下的力學性能［8］。鄧文中等討論了重慶石板坡長江大橋復線橋總體設計中采取的預應力鋼束布置方案［9］。謝燕梅基于溫州甌江大橋對混合梁剛構橋的體外預應力線形進行了優化［10］。陳群等介紹了中山小欖水道混合梁剛構橋中體外預應力的設計思路［11］。

以往研究主要分析了體外預應力在傳統大跨徑混凝土剛構橋中所發揮的作用，以及現有混合梁剛構橋中體外預應力的布置方式，但對體外預應力鋼束的具體作用效果與設置方法研究不多。為此，本文依托福建泉州安海灣大橋的體外預應力鋼束設置，進行了相關的計算分析，得到預應力鋼束的合理設置方法，為同類橋梁的設計提供參考。

1 工程概述

安海灣大橋上部結構為三跨混合梁剛構橋，總體布置如圖1 所示，跨徑布置為135 m+300 m+135 m，總長570 m。跨中鋼箱梁吊裝段長度為103 m，重1 272 t，鋼箱梁兩端通過5 m 長的鋼混結合段與混凝土箱梁連接，目前是世界第二大跨度的混合梁剛構橋，2020 年3 月26 日全橋合龍。主梁按雙幅布置，全寬33.5 m，上、下行分幅布置。主梁高度4.5～15 m，其中鋼箱梁梁高范圍4.535～5.869 m。墩頂梁高15 m，高跨比為1∶20，跨中梁高4.5 m，高跨比為1∶66.152。混凝土主梁、鋼混結合段及鋼主梁三部分梁高均按2 次拋物線規律變化。主墩采用雙薄壁等截面墩，墩高22.89 m。

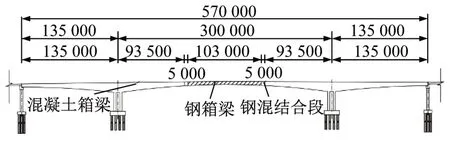
圖1 安海灣大橋總體布置圖（單位：mm）Fig.1 General arrangement of the Anhaiwan Bridge（Unit：mm）

安海灣大橋采用了體內外混合配束的方式。體內預應力束布置與常規混凝土連續梁相似，主要是防止混凝土箱梁出現較大拉應力。具體方法是在箱梁頂板布置縱向預應力束和橫向預應力束，在腹板布置縱向下彎預應力束和豎向預應力束，在底板布置縱向合龍預應力束，體內預應力鋼束隨著混凝土節段懸澆逐段張拉。體外預應力主要是為防止主跨跨中下撓，其布置如圖2 所示。總體上可分為混凝土梁中的體外預應力與鋼箱梁中的體外預應力兩部分，共設置了8 對18Φs15.2的體外預應力，沿梁中心線對稱分布。體外預應力鋼束沿縱橋向變化分為12 個部分，編為1～12號鋼束。其中：1號為8根18Φs15.2的鋼絞線；2號為 6 根 18Φs15.2 的鋼絞線；3 號為 4 根 18Φs15.2 的鋼絞線；4 號為 2 根 18Φs15.2 的鋼絞線；5～8 號均為 2 根 18Φs15.2 的鋼絞線；9 號為 2 根 18Φs15.2 的鋼絞線；10 號為 4 根 18Φs15.2 的鋼絞線；11 號為 6根 18Φs15.2 的鋼絞線；12 號為 8 根 18Φs15.2 的鋼絞線。成橋時體外預應力鋼束僅張拉控制應力的30%（即558 MPa）。

圖2 安海灣大橋體外預應力布置（單位：mm）Fig.2 Layout of the external prestressing tendons in the Anhaiwan Bridge（Unit：mm）

2 體外預應力鋼束的作用效應分析

2.1 計算分析方法

建立全橋板殼-實體有限元模型，混凝土箱梁采用SOLID95 實體單元模擬，鋼箱梁采用SHELL181 板殼單元模擬，預應力鋼束采用LINK10 單元模擬，全橋模型單元數量約60 萬個，結構整體模型如圖3所示。

圖3 安海灣大橋板殼-實體有限元模型Fig.3 Shell-solid finite element model of the Anhaiwan Bridge

2.2 設計線形體外預應力總體效應

首先計算僅在自重荷載作用下，鋼箱梁段整體的豎向位移如圖4 所示，中部位移大而端部位移小，跨中豎向位移最大，為641.8 mm；最小位移發生在端部，為429.2 mm。

圖4 自重作用下鋼箱梁部分豎向位移圖（單位：mm）Fig.4 Deflection of steel girder under self-weight（Unit：mm）

在自重荷載作用下，部分混凝土箱梁截面應力如圖5 所示，截面上緣受拉而下緣受壓，越靠近中墩的截面應力越大。墩頂附近截面的最大壓應力為17.55 MPa，最大拉應力為18.35 MPa；混凝土梁中部附近截面最大壓應力為15.58 MPa，最大拉應力為10.01 MPa；結合段附近截面最大壓應力為13.12 MPa，最大拉應力為3.87 MPa。

當再考慮體外預應力作用時，鋼箱梁跨中豎向位移為628.72 mm，鋼箱梁端部位移為421.2 mm。對比計算結果，施加體外預應力能夠有效減小鋼箱梁跨中和端部撓度分別為13.1 mm、8.0 mm。此外，設置體外預應力使得下緣壓應力減小幅度為0.20～0.30 MPa、上緣拉應力減小幅度為0.80～1.00 MPa。

2.3 體外預應力效應局部分析

由于體外預應力鋼束主要由混凝土箱梁段的鋼束和鋼箱梁段的鋼束構成，因此將二者分別施加至主梁上，進一步分析二者對于減小跨中撓度所能做出的貢獻。

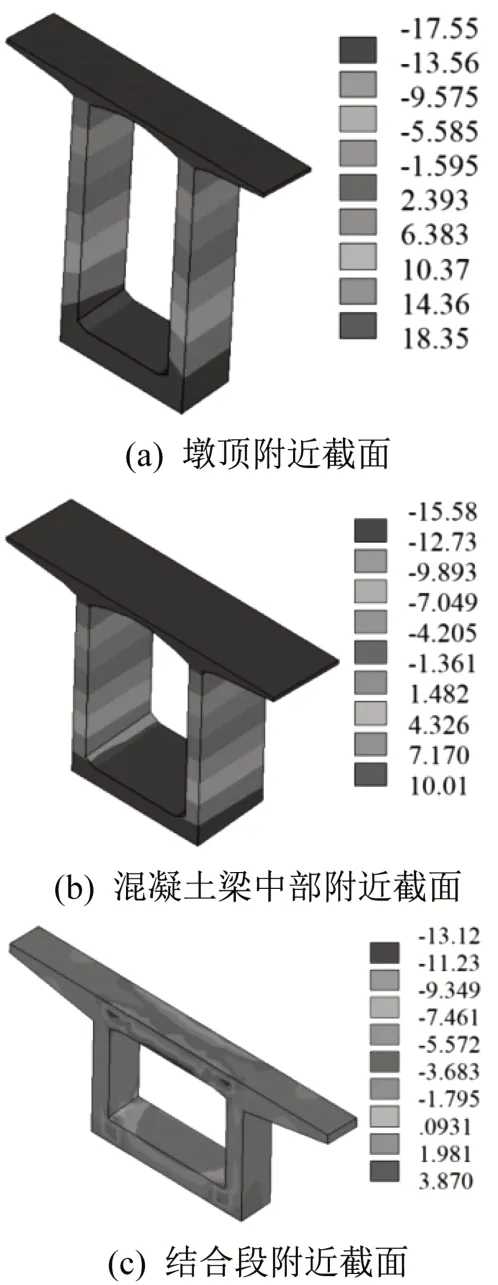
圖5 自重作用下部分混凝土箱梁截面應力圖（單位：MPa）Fig.5 Stress diagrams of concrete girder sections under self-weight（Unit：MPa）

2.3.1 混凝土箱梁段體外預應力

在體外預應力初始線形的基礎上，去掉鋼箱梁段的體外預應力，僅保留混凝土箱梁段的體外預應力，包括 1～7 號及 9 號、10 號鋼束，具體線形如圖6所示。

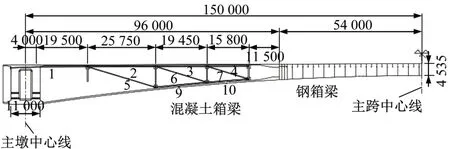
圖6 混凝土箱梁段體外預應力線形（單位：mm）Fig.6 Layout of the external prestressing tendons in concrete girders（Unit：mm）

在自重與體外預應力共同作用下，鋼箱梁段跨中位移減小9.7 mm，端部位移減小9.4 mm，占據了體外預應力總效應的74.50%與117.94%。

此外，相較于設計線形的體外預應力作用，僅布置混凝土梁段范圍體外預應力，混凝土梁截面下緣壓應力減小幅度降低，而上緣拉應力減小幅度提高，有利于梁段受力。

2.3.2 鋼箱梁段體外預應力

在體外預應力初始線形的基礎上，去掉混凝土箱梁段的體外預應力，僅保留鋼箱梁段的體外預應力，為了保證預應力的有效性，將線形延伸至混凝土箱梁中最接近鋼梁的轉向塊內，包括8 號、11號及12號鋼束，具體線形如圖7所示。

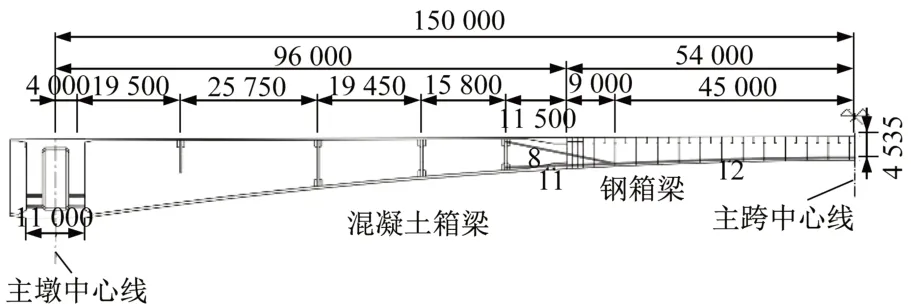
圖7 鋼箱梁段部分體外預應力線形（單位：mm）Fig.7 Layout of the external prestressing tendons in steel girder（Unit：mm）

計算表明，僅施加鋼箱梁段體外預應力時鋼箱梁段跨中位移減小3.3 mm，端部位移增大了1.5 mm；同時，混凝土梁截面下緣壓應力降低，而上緣拉應力提高；而對于結合段附近截面，拉壓應力均一定程度增大；不利于梁段受力。

初始線形下體外預應力總用量為2.95 m3，混凝土箱梁體外預應力總體積為1.65 m3，占比56%；鋼箱梁體外預應力總體積為1.30 m3，占比44%。對于減小鋼箱梁跨中豎向位移，混凝土箱梁體外預應力貢獻了75%，而鋼箱梁部分貢獻了25%。并且，混凝土箱梁的體外預應力能一定程度上改善混凝土梁的受力。因此，將材料用量與實際貢獻對比可知，在混凝土箱梁設置體外預應力更加經濟有效。

結合混合梁剛構橋的彎矩分布可知，當鋼箱梁長度與主跨長度比例為0.36 時，恒載作用下中跨混凝土梁以受負彎矩為主，鋼箱梁則以受正彎矩為主。同時由于采用了鋼箱梁，跨中正彎矩較小，因此，在混凝土段設置預應力能更有效地減小鋼箱梁段的豎向位移。

根據上文分析，施加體外預應力在一定程度上可以減小鋼箱梁豎向位移，尤其是跨中截面的豎向位移。若要進一步發揮體外預應力的經濟性和有效性，應該將體外預應力的布置優先集中在混凝土箱梁中；而結合段附近體外預應力有助于增大壓應力，使鋼-混結合更緊密，因此保留8 號與11 號鋼束，并錨固至結合面處。得到初步優化線形如圖8所示。

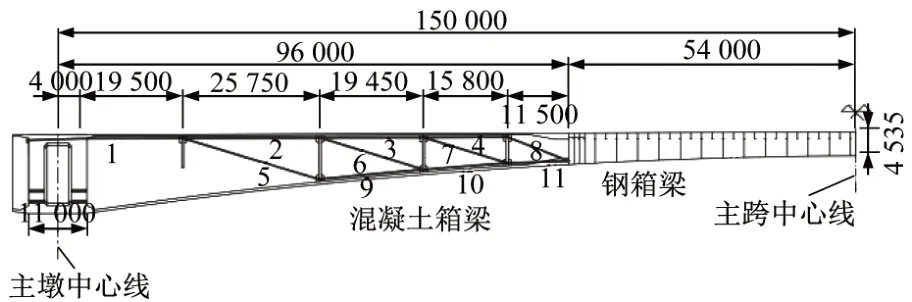
圖8 體外預應力初步優化線形（單位：mm）Fig.8 Initial optimization of layout of the external prestressing tendons（Unit：mm）

2.4 體外預應力效應逐段分析

為進一步分析每根體外預應力所發揮的作用，取如圖9 所示的3 段鋼束，分別建模，分析1號、5 號與9 號鋼束單獨作用時的效應，位移結果表1所示。

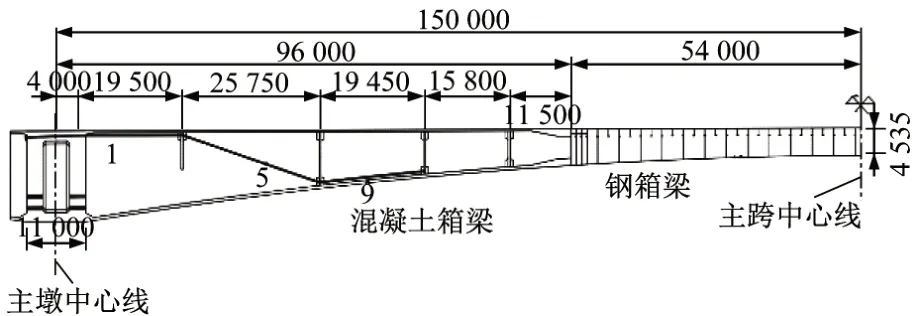
圖9 體外預應力優化分析線形（單位：mm）Fig.9 Layout of the external prestressing tendons for analysis（Unit：mm）

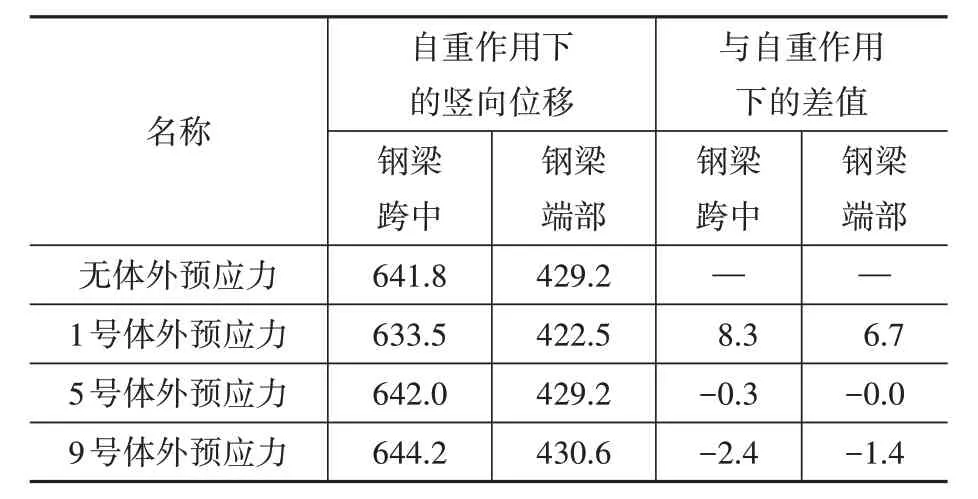
表1 體外預應力位移效應逐段分析Table 1 The displacement effects of every external prestressing tendon mm

由表中數值看出：1 號鋼束作用下，鋼箱梁跨中位移減小8.3 mm，端部位移減小6.7 mm；墩頂附近截面下緣壓應力有所減小，而上緣拉應力明顯減小。5 號鋼束作用下，鋼箱梁段跨中位移增大了0.3 mm，端部位移增大了0.03 mm；混凝土梁段的中間截面附近最大壓應力有所增大。9 號鋼束作用下，鋼箱梁段跨中位移增大了2.4 mm，端部位移增大了1.4 mm；混凝土梁段受力基本不變。由此可見，布置在靠近箱梁頂板附近的1 號鋼束對改善跨中梁體下撓的效果最好；而沿底板附近布置體外預應力反而增加了梁體跨中的下撓，主要原因是該段預應力鋼束在向跨中呈斜向上的線形造成的。

3 體外預應力鋼束優化

3.1 優化方案

通過對體外預應力鋼束的局部分析，可以發現將體外預應力布置在混凝土箱梁段內更有效，從而得到了如圖8 所示的初始優化線形。進一步以1 號、5 號與9 號鋼束為例進行受力分析，將混凝土箱梁段內的體外預應力鋼束分為頂板平行束、斜向束及底板平行束三部分，可知1～4號頂板平行束能減小鋼梁位移且優化混凝土段受力，5～8 號斜向束對混凝土段受力有利，9～11 號底板平行束則不利于鋼梁位移減小。因此，在初始優化線形的基礎上，去除混凝土箱梁中的底板平行束，即保留1～8 號鋼束，得到最終優化線形如圖10所示。

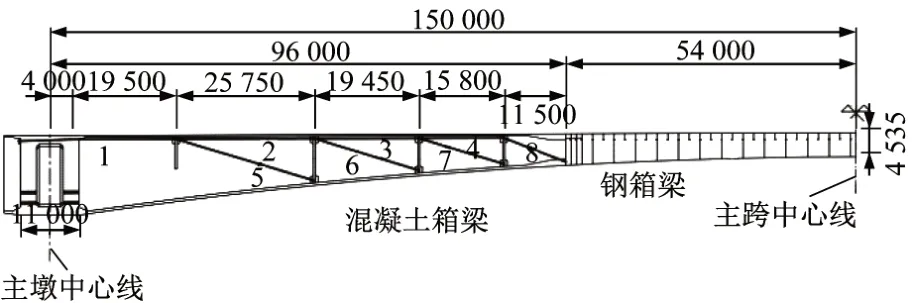
圖10 體外預應力優化線形（單位：mm）Fig.10 Optimal layout of the external prestressing tendons（Unit：mm）

3.2 優化線形下體外預應力效應

在自重與優化后的體外預應力作用下，鋼箱梁豎向位移中間大而兩邊小，最大豎向位移發生在跨中，為625.7 mm；最小豎向位移發生在端部，為416.6 mm。從而與自重作用下相比，鋼箱梁段跨中位移減小16.1 mm，端部位移減小12.6 mm。相較于原始體外預應力線形作用下的結果，二者分別擴大了23.3%與58.1%，有效性顯著增強。

在改善一般混凝土梁截面受力方面，與設計線形相比，截面下緣壓應力減小幅度更小，為0.10～0.25 MPa；而截面上緣拉應力減小幅度則有所增大，為1.15～1.50 MPa；并且結合段附近截面拉壓應力均減小。總體而言，優化線形的體外預應力布置方式更有利于結構受力。

4 預應力鋼束索力調整預案

傳統大跨徑預應力混凝土連續剛構橋在使用過程中，由于收縮徐變等長期效應影響，跨中撓度會大幅度增加，影響其正常使用功能。為了探究混合梁剛構橋在長期效應下的變形，利用有限元模型進行模擬。由于成橋時體外預應力張拉應力僅為控制應力的30%（558 MPa），因此當使用過程中出現較大撓度，可以對體外預應力進行再張拉，以減少主跨的撓度。在考慮混凝土10年收縮徐變的基礎上，分別將體外預應力再張拉至控制應力的40%（744 MPa）、50%（930 MPa）、60%（1 116 MPa）、70%（1 302 MPa）及75%（1 395 MPa），計算各自的作用效果，計算結果如表2 所示，與長期作用導致的位移增大值相比，跨中位移減小程度較小，且呈線性增長，可根據實際的撓度變化選擇合適的調整預案。

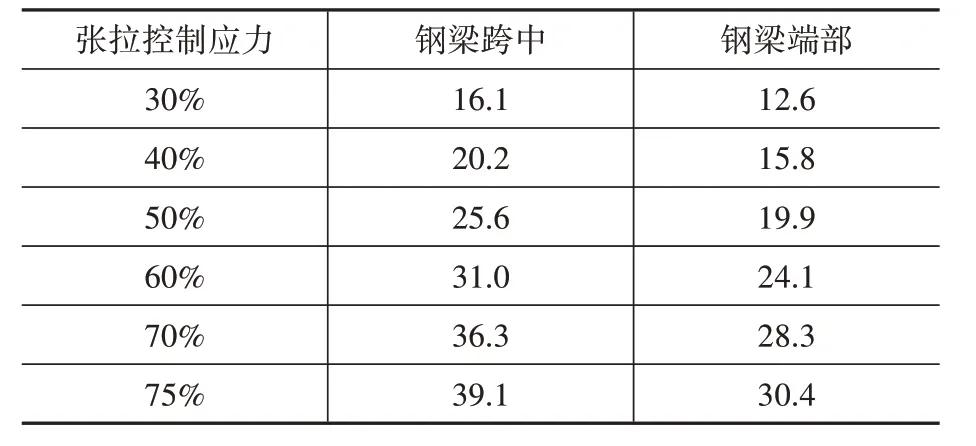
表2 不同張拉控制應力下鋼梁段豎向位移減小值Table 2 The deflection decreases under different tension control stresses mm

5 結 論

（1）本文以泉州安海灣大橋為背景工程，通過有限元方法，對體外預應力在減小混合梁剛構橋跨中鋼梁段豎向位移，以及改善混凝土段受力性能中所能發揮的作用，進行了整體與局部的分析。

（2）通過有限元模型逐段分析體外預應力的效應，以改善跨中鋼梁撓度和混凝土梁體受力為原則，對體外預應力的布置進行優化，發現僅保留混凝土梁段中的頂板水平束及斜向束時，體外預應力所能發揮的效果更好。

（3）計算了安海灣大橋在收縮徐變等長期效應作用下再張拉體外預應力時跨中鋼箱梁的變形，得到不同體外預應力再張拉調整預案對減小鋼梁豎向位移的作用。