基于有限元分析的浮選多相流研究

尹洪月 馬永杰 殷雨峰 王大碩 曹 陽

（黑龍江科技大學 礦業工程學院，黑龍江 哈爾濱150022）

基于ANSYS有限元對浮選多相流進行研究，就目前國內選煤廠而言機械攪拌式浮選機被廣泛應用，但由于其可視性差，且浮選機內流體狀態復雜，因此研究浮選機內多相流很是困難。但本次項目采用有限元分析方法，可以即快捷又高效的模擬浮選機內的流體狀態，并分析浮選機內流體的狀態并給出可靠的動力學方程，并可用于浮選機的工藝參數優化指導生產，因此具有較廣闊的應用前景。

1 有限元分析法

定義。其基本思想是將求解區域用矩形網格代替,網格線的交點為計算節點，每個節點與相鄰的四個網格組成一個計算單元,即一個計算單元由一個中心節點與一個相鄰節點組成。在每個單元中函數的近似解不是像有限元方法那樣采用單元基函數的線性組合來表達，而是以單元中未知函數的分析解來表達。為了獲得單元中的分析解,單元邊界條件采用插值函數來逼近,在單元中把控制方程中非線性項局部線性化,并對單元中待求函數的組合形式做出假設,找出其系數,用單元邊界節點上待求函數值來表達。雖然有限分析解獲得的是求解區域中離散點的函數值,但是由于每個單元內部都有與其中心節點對應的分析解表達式,因此有限分析解在每一個節點的局部區域內都是連續可微的,這對于需要計算求解函數導數的計算流體力學問題具有明顯的優勢。

2 有限元模型的建立

2.1 轉子模型的建立。轉子應用材料為Q235A，該材料屈服極限為265MPa、材料許用應力為157MPa、彈性模量2.1×105N/mm2、泊松比為0.3、質量密度為7850kg/m3、熱膨脹系數為273.33×10-5K、切邊模量80GPa。進行網格劃分和模型如圖1 所示。

圖1 網格劃分模型

2.2 邊界條件及加載。根據浮選機的實際使用狀況，將槽底的8 塊座板設置為固定約束，在槽底表面施加P=3.8×104Pa 的壓力，其他各處保持不變，不加約束。

2.3 求解及結果分析。按上述邊界條件加載后，對該模型進行求解，其等效應力云圖如圖2 所示，位移矢量和圖如圖3 所示。

圖2 初步設計的槽底應力云圖

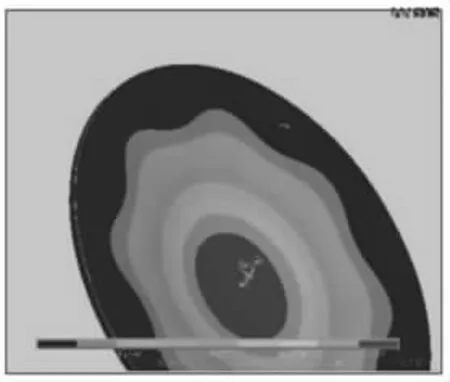
圖3 初步設計的槽底位移矢量和圖的槽底應力云圖

由圖2 可知，根據彈性理論計算時，其應力最大點是在靠近槽底中心方向的座板與肋板的連接處。在工作情況下，槽底載荷的最大Von-mises 應力為σmax=692.16MPa＞[σ]，在許用應力范圍內，其他區域應力不超過163.186MPa。由此可見，該結構中存在著明顯的應力集中現象，且不能滿足強度要求，需進一步改進。

由圖3 可知,在槽底中心區域出現了較大的矢量和位移。通過理論受力分析可得知,該位移主要為受力變形，為達到減小槽底中心位移量的目的，需從提高結構彎曲剛度方面考慮優化改進。

3 單一液相流模擬與分析

3.1 數值模擬策略。

3.1.1 湍流模型的選擇。在大量專家學者的試驗，通過大量的計算與實踐總結眾多的模型，包括雷諾應力模型、大渦模擬模型、Spalart-Allmaras 模型、k-ω 模型、k-ε 模型在內的經典數學模型。攪拌流場中應用最多的是Spalding 和Launder 提出的標準k-ε模型[8]。該模型主要求解湍流動能k 和湍流耗散率ε，將二者與湍流渦粘系數μt 建立相應的關系，k 方程的求解較為精確，但是，ε方程是經過經驗公式推導出來的。因為標準k-ε 模型簡單、計算精度高等特點，于是該模型得到廣泛應用。在標準k-ε 模型的推演中引入了Boussinesq 假設和v=Ck2/ε 的關系式，特征速度以湍流動能的形式反應，特征長度的尺度用湍流動能耗散率進行表征，使k-ε 在流場數值模擬過程中有以下兩個獨到之處。

在前期作用中，考慮到流場中各個流動點的湍流動能傳遞和流動，沒有根據經驗設定其特征長度，而是通過耗散尺度進行表征的。

標準k-ε 模型的湍流動能方程（k 方程）為：

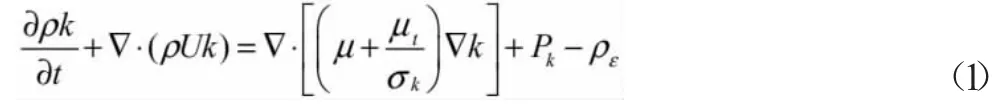
標準k-ε 模型的湍流動能方程（ε 方程）為：

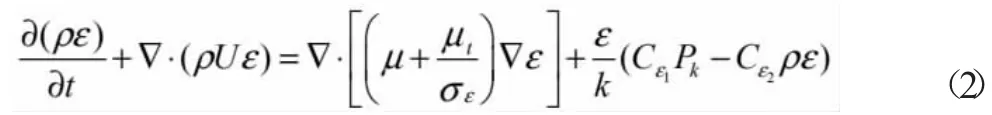
Pk是粘性力和浮力的湍流產物，其方程為：

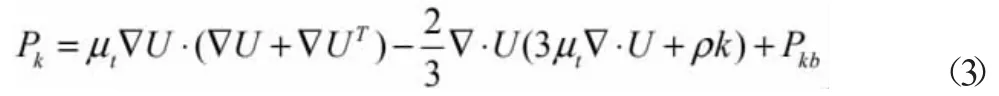
3.1.2 壁面的邊界條件。流體在壁面處的流動狀態可設置為兩種，分別為無滑移和自由滑移，具體的選擇，需要根據數值模擬的情況。根據無滑移壁面的特性和條件，其適用于壁面間與流體相互作用的流體模擬；自由滑移條件適用于壁面與流體無相互作用、流體在與界面垂直方向無速度梯度的條件。由于液相粘度對模擬的影響較大，在單一液相數值模擬中，適合采用無滑移邊界條件，即No Slip 模型。

3.1.3 動靜區域的交界面。在劃分旋轉域的過程中，會產生交界面，而設置交界面的好壞，會直接影響模擬數值的結果。決定數值模擬精確性的關鍵所在是固體域與流體域的交界面和流體域內動- 靜域交界面的設置。交界面設置需要適合流動域與固定域相對位置保持不變的流場，因此，選擇CFX多重參考系坐標中提供的凍結轉子模型。

3.2 攪拌導流區流場。

3.2.1 特征。根據以上設定條件的敘述，對于絮凝浮選裝置的攪拌導流區進行了單一液相流場的特征數值模擬，其收斂曲線如圖4所示，其中由殘差收斂曲線（紅色線）可以了解到，其殘差基本處在0.0015，數值模擬具有很好的收斂性，滿足流場數值模擬的應用。采用CFX-Post 后處理模塊建立絮凝浮選裝置的主視截面和俯視截面，對流場進行分析。

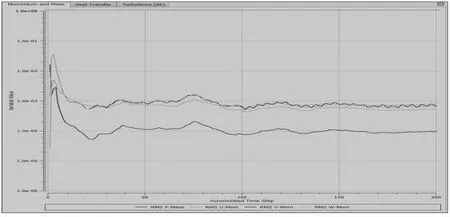
圖4 單相流模擬運算收斂圖

在攪拌作用下與壁面發生碰撞，改變運動方向，進入到轉子上下的兩個軸向循環區域內。因為中部循環距離高速旋轉攪拌的轉子最近，所以受其影響中部循環區域流體的流速比較大，特別是在靠近轉子的區域，其速度達到最大值。

3.2.2 攪拌導流區單一液相湍流動能分布特征。由微細顆粒礦物形成大顆粒絮凝體的過程，湍流剪切力起著必不可少的作用，它是絮凝體的成長的主要動力來源的同時，也是會對之前已經成型的大顆粒絮凝體造成相應的破壞。所以在絮凝過程中，對其進行合理的控制至關重要，使其在一個合理的范圍內，既能達到既使絮凝體生長的范圍，又不會使得已經成型的絮凝體遭到破壞，而湍動能可用來表示湍流剪切力和絮凝體的密實程度，其表示形式為：

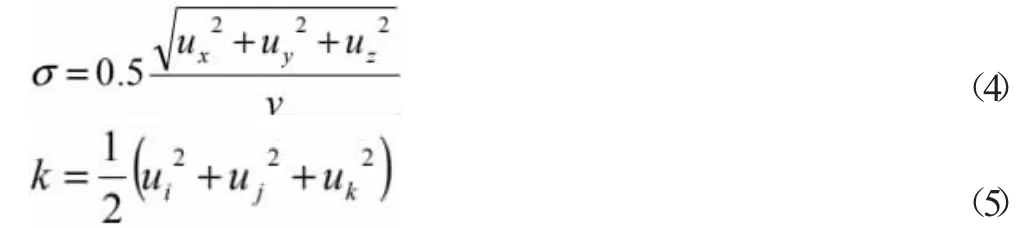
而在所采用的標準k-ε 模型中，湍流動能則表示形式和上面的表達式存在著線性關系。因此采用CFX軟件中的湍流動能K值作為攪拌導流區評價標準，也就是在一定范圍內，隨著k 值的增加，湍流動能也會更加劇烈，同時流場內微渦比例也會增加，從而絮凝效果好。

模擬結果顯示，轉子葉輪上方位置產生了湍流動能最大區域，其中導流管一側的湍流動能顯然要低于遠離導流管區域的湍流動能，這符合了素的分布情況。這主要是由于該處的剪切效果被導流管的導流運輸作用減弱了。在轉子區域中，葉片的高速旋轉驅動流體的運動，從而產生了強烈的湍流動能，而轉子的運動是影響湍流強度的主要因素。在轉子區域，由于轉子的攪拌作用，使流體形成了高速而強烈的湍流脈動，從而該區域發生絮凝反應。在遠離轉子的其他區域，流體的速度逐漸減小，湍流受葉片運動的影響逐漸減弱，相應的，也降低了流體的湍流動能。這主要是由于流體的粘滯作用和能量耗散引起的，絮凝體的碰撞粘結受益于在該區域內的流體運動，進而使絮凝體的粒徑生長較大。

4 結論

單相結果表明，在攪拌流暢的導流區內，存在三個不同的循環區域，自轉區域出現最高湍流動能，對礦物顆粒的絮凝有利。計算G值可得到，模擬轉速范圍在635r/min～870r/min 之間。通過對不同轉速、轉子位置以及導流筒結構的設置情況進行模擬，得出的優化條件為轉子距底350mm，轉速800r/min，設置導流筒。此時湍流動能1.425m2s-2，礦漿最大流速1.64m/s。此時的礦漿流動及循環狀態最好，整個流場對微細粒礦物的絮凝有利。