基于連續回轉電液伺服馬達模糊RBF神經網絡控制研究

范文靜， 王曉晶， 孫培元， 何超群， 劉亞楠， 李 巖

(哈爾濱理工大學 機械動力工程學院， 黑龍江 哈爾濱 150080)

引言

從20世紀初開始，航空航天工程得到了飛速發展，這對于當代科技進步和國民經濟生產有著深遠的影響。為更方便的模擬和復現航空航天飛行器的姿態角和姿態角速度的變化，實驗室常用液壓仿真轉臺模擬飛行狀態，并針對系統的特性和性能要求設計控制器，使系統在復雜的干擾環境中也能滿足設計要求，這對提高航空航天飛行器的導航精度具有十分重要的意義。連續回轉電液伺服馬達作為液壓仿真轉臺的核心設備，在工作過程中存在摩擦、泄漏等非線性以及內外部環境的不確定性因素的影響，嚴重降低了電液伺服系統的性能，為此要使電液伺服系統存在上述因素干擾時，依舊能保證系統對超低速、高精度、高頻響的特性要求，成為了航空航天研究領域的熱點之一[1-2]。文獻[3]采用灰箱辨識的方法得到電液伺服系統的模型，并設計了模糊自適應PID控制器進行仿真實驗，驗證了該控制策略提高了系統的響應頻率。文獻[4]為拓寬系統的頻帶提出了基于魯棒控制理論的混合靈敏度控制策略，從而抑制了外界干擾以及不確定性等非線性因素對系統性能的影響。針對連續回轉電液伺服馬達中參數時變及非線性等因素，自適應魯棒控制策略被提出并廣泛應用于液壓執行器、負載模擬器和懸架系統中[5-7]。

本研究根據RBF神經網絡的高度非線性擬合優點，提出了一種基于模糊RBF神經網絡控制的策略，將模糊理論中的隸屬度函數和模糊規則運用在RBF神經網絡的隱含層中，提高了神經網絡的自學習、自組織能力，再利用遺傳算法優化模糊RBF神經網絡的初始權值、閾值和中心寬度，并由梯度下降法進行更新，以提高網絡的控制精度，使系統具有更高的跟蹤精度和穩定性[8]。

1 連續回轉電液伺服馬達工作原理

連續回轉電液伺服馬達原理如圖1所示。馬達在工作時，液壓泵為馬達提供壓力油，油源壓力通過溢流閥進行調定，油液通過電液伺服閥P1口經過控制油路分別到達進油腔1和進油腔2。然后由進油腔進入馬達工作容腔，直接作用于馬達葉片，從而使葉片轉動，并帶動馬達轉子旋轉，輸出相應的轉矩和轉速。馬達定子內曲線由多條八次曲線組成，其中包括2條短半徑圓弧，2條長半徑圓弧和4條連接短半徑與長半徑圓弧之間的過渡曲線。馬達葉片為13個，對稱分布，每個葉片根部都安裝有預緊彈簧。同時，在過渡圓弧處，在配油盤上加工配油機構，使葉片頂部與根部的油路相通，在長短半徑圓弧處，通過調定減壓閥壓力，使減壓油通入葉片根部，這樣保證了馬達在旋轉時葉片始終與定子內壁相接觸，從而形成密封容腔。當馬達葉片運動到回油腔位置時，隨著葉片的不斷旋轉，密封容腔的體積不斷減小，液壓油通過回油腔1和回油腔2流回控制油路，經過電液伺服閥P2口流回油箱。馬達內部泄漏的油液經泄漏油路流回油箱，泄漏油路由短虛線表示。

圖1 連續回轉電液伺服馬達原理圖

2 連續回轉電液伺服馬達數學模型的建立

2.1 伺服閥閥口線性化流量方程

QL(s)=KqXv(s)-KcpL(s)

(1)

式中,QL—— 液壓馬達的負載流量，m3/s

Kq—— 流量增益，m2/s

Xv—— 閥芯位移，m

Kc—— 流量壓力系數，m3/(s·Pa)

pL—— 外負載壓力，Pa

2.2 液壓馬達的負載流量連續性方程

連續回轉電液伺服馬達運轉時受外界干擾以及自身摩擦等所產生的內泄漏和外泄漏損失的流量，正常工作時所需的流量，以及由液體壓縮產生的附加流量，這3部分的流量構成了連續回轉電液伺服馬達的總負載流量，故有：

(2)

式中,Dm—— 弧度排量，m3/rad

θ—— 角位移，rad

Ctm—— 總泄漏系數，m3/(s·Pa)

Vt—— 連接管道、回轉馬達及電液伺服閥，閥腔的總容積，m3

βe—— 有效體積彈性模量，Pa

2.3 馬達系統力矩平衡方程

連續回轉電液伺服馬達正常工作時所需要的各部分力矩之和與外負載之間力矩的平衡方程，可通過牛頓第二定律獲得：

DmpL(s)=Jtθ(s)s2+Bmθ(s)s+Gθ(s)+TL(s)

(3)

式中,Jt—— 馬達及外負載折合后的總轉動慣量，

kg·m2

Bm—— 黏性阻尼系數，N·m·s/rad

G—— 負載的彈簧剛度，N·m/rad

TL—— 作用在馬達軸上的任意外負載力，N·m

2.4 閥控馬達動力系統傳遞函數

連續回轉電液伺服馬達的輸出角位移θ(s)，是由馬達運轉中伺服閥閥芯的位移Xv(s)以及在外界摩擦干擾TL(s)下馬達的位移同時構成的，可由上式(1)～式(3)計算得到。

(4)

式中,Kce為閥控馬達總流量-壓力系數，m3/(s·Pa)，Kce=Kc+Ctm。

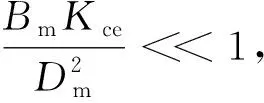
式中,ωh—— 無阻尼液壓固有頻率，rad/s，

ξh—— 液壓阻尼比(無量綱)，

2.5 電液伺服閥傳遞函數

在進行電液伺服閥傳遞函數建立過程中，不能忽略電液伺服閥對控制系統的影響，則將其簡化為二階振蕩環節，則：

(6)

式中,Ksv—— 空載流量增益，m3/(s·A)

ωsv—— 等效無阻尼自振頻率，rad/s

ξsv—— 等效阻尼系數(無量綱)

2.6 伺服放大器傳遞函數

由于系統的液壓固有頻率高于伺服放大器的頻帶范圍，則在進行連續回轉馬達系統設計時忽略伺服放大器的動態性能，因此可簡化伺服放大環節為比例環節，則有：

(7)

式中,Ka為放大器的增益,A/V。

2.7 連續回轉電液伺服馬達的系統傳遞函數

由式(1)～式(5)可構建如下傳遞函數方框圖，如圖2所示。

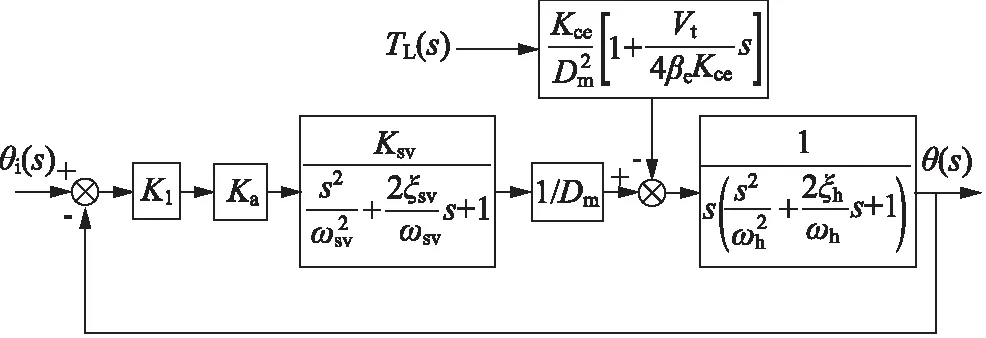
圖2 伺服系統傳遞函數方框圖

圖2中，θi(s)為連續回轉馬達電液伺服系統的輸入信號，θ(s)為其輸出信號，K1為電液伺服系統主控制器的傳遞函數，TL(s)為外加的摩擦力矩。因此連續回轉馬達電液伺服系統的開環傳遞函數如下：

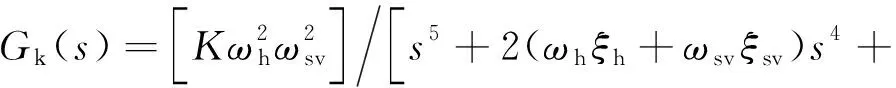
(8)

2.8 連續回轉電液伺服馬達參數設置

采用專門針對連續回轉馬達電液伺服系統的實驗臺進行相應實驗，實驗臺的各項參數分別有：葉片式連續回轉馬達的弧度排量為Dm=1.59×10-4m3/rad；負載慣量為Jt=10 kg·m2；油源壓力為12 MPa；一般室溫條件下，油液體積彈性模量為βe=7×108 N/m2；伺服閥和連續回轉馬達及其相關組件的有效容積之和為Vt=1.21×10-3m3；電液伺服系統的液壓固有頻率為ωh=92.63 rad/s，阻尼系數取ξh=0.1；黏性系數Bm=5543 N·m·s/rad；泄漏系數Kce=7×10-12m3/(s·Pa)；實驗臺選用的電液伺服閥的型號為SF106-10，且額定電流為8 mA，額定壓力為ps=16 MPa時，電液伺服系統的額定流量為30 L/min；等效阻尼系數ξsv=0.6，得到流量增益為Ksv=0.04941 m3/(s·A)；伺服放大器輸出控制電壓的飽和值取±10 V，可以得到相應的增益為Ka=0.0008 A/V。

由以上所得系統參數可以得到系統對輸入信號響應的開環傳遞函數為:

GK(s)=

(9)

若忽略伺服閥動態特性，將其簡化為比例環節，可以得到系統對輸入信號響應的開環傳遞函數為:

(10)

連續回轉馬達電液伺服系統的開環頻率特性分析，如圖3所示，系統的幅值裕度為149 dB(0.2486 rad/s)，相角裕度為89.9°(92.6300 rad/s)，該電液伺服系統的幅值裕度和相角裕度表征其穩定性，由特性曲線可知電液伺服系統穩定性較差，響應頻率較低，跟蹤性能不好。

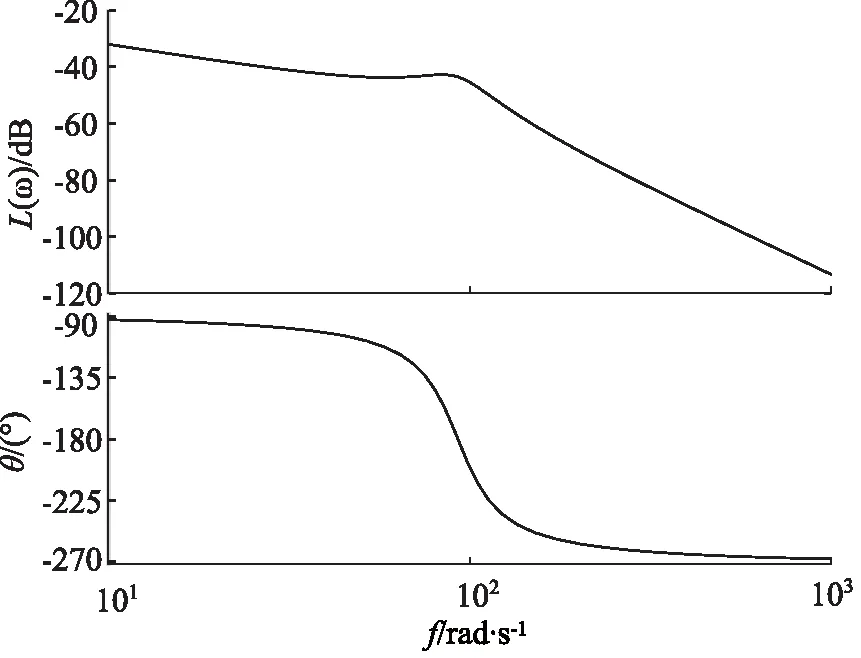
圖3 開環系統的頻率特性分析圖

3 模糊RBF控制算法

RBF神經網絡是前饋型神經網絡，包括輸入層、隱含層以及線性神經元輸出層三層結構。其中隱含層選擇高斯激活函數作為神經元激活函數。RBF神經網絡的優點是高度非線性擬合，同時其結構簡單，訓練速度快，但容易陷入局部最優解，通常將RBF神經網絡與模糊機制相結合、利用啟發式算法等方法可進一步改善，達到提高算法精準性的目的。

3.1 模糊RBF神經網絡結構

模糊RBF神經網絡是由網絡輸入層、模糊化層、模糊推理層和輸出層4層結構構成的前饋型神經網絡，可以同時為神經網絡提供模糊輸入信號和模糊權值。本研究選擇各網絡層的神經元個數分別為2-3-3-1，網絡結構如圖4所示，其中x代表神經元輸入，即連續回轉馬達電液伺服系統給定角度輸入；y為連續回轉馬達電液伺服系統實際輸出；cij為模糊化層高斯函數的中心寬度；bi為其閾值；vj為模糊推理層與輸出層之間的連接權值，ym為電液伺服系統經過模糊RBF神經網絡控制的輸出值[10-14]。

圖4 模糊RBF神經網絡結構

其中，模糊RBF神經網絡的結構層為如下：

(1) 輸入層各節點的輸出值為：

f1(i)=xi

(11)

(2) 隸屬函數層的第j個節點表示為：

(12)

公式(12)中的參數有：X為系統輸入和輸出信號構成的2維向量；cij和bj分別為隸屬函數層的第i個輸入變量的第j個模糊集合高斯函數的中心寬度值和閾值，||X-cij||為向量X-cij的范數，衡量向量X與cij之間的歐式距離。

(3) 模糊推理層表示為以下值：

f3(n)=∏f2(j),n=1,2,3

(13)

其中，f3(n)為第三級模糊推理層的輸出，即第二層各節點輸出之積，n表示第三層的節點數。

(4) 輸出層為：

f4(·)=∑vj·f3(n),n=1,2,3

(14)

式中,vj為輸出層節點與模糊推理層節點之間的連接權值。

3.2 模糊RBF神經網絡更新公式

本研究選擇梯度下降法對網絡的中心寬度、閾值和權值進行更新，其中y為連續回轉馬達電液伺服系統實際輸出，ym為模糊RBF神經網絡的輸出值，若采用梯度下降法進行調整，則定義網絡的損失函數為：

(15)

權值函數vj、中心寬度cij、閾值bj的更新公式分別如下所示：

vj(k+1)=vj(k)+ηe(k)·f3(j)+α(vj(k)-

vj(k-1))cij(k+1)

α(cij(k)-cij(k-1))bj(k+1)

α(bj(k)-bj(k-1))

(16)

式中,η為學習速率；α為動量因子，且η∈(0,1),α∈(0,1)，一般情況下η過小會增加迭代次數使運算量變大，過大則導致算法無法收斂，因此取η=0.7,α=0.08。

3.3 模擬遺傳退火算法優化初始值

在模糊RBF神經網絡中，隸屬層高斯函數的中心寬度cij、閾值bj和權值函數vj的初始值的選擇極大程度上影響了算法的收斂性，若選擇過大造成算法難以收斂至最優值，選擇過小則會導致算法計算量大擬合精度下降甚至發散不能得到最優解，因此，選擇智能優化算法進行搜索優化，本研究選擇模擬遺傳退火算法進行初始值優化，即可以在可行解域內進行并行化求解，且使全局最優解以概率為1在可行域內被收斂，避免陷入局部最優解中[15-16]。

因此，模擬遺傳退火算法的初始值尋優步驟如下：

步驟1：二進制編碼 采用10位長度，二進制編碼方式對閾值bj、中心寬度cij和權值函數vj進行編碼。

步驟2：參數初始化 一般設樣本個數P0=50，迭代步驟為N=150，交叉概率Pm=0.8，并設置初始溫度為T0=100 ℃，退溫率為λ=0.95；由于選擇的模糊RBF神經網絡的訓練步驟為1000步，網絡層數分別為2-3-3-1，且i=1,2,j=1,2,3。

步驟3：評價機制 采用適應度函數來評價當前種群中的各個樣本，根據評價原則選擇最優的一組值，若滿足終止要求，則輸出結果，否則進入循環求解，則有適應度函數為網絡損失函數的倒數。

步驟4：選擇復制、交叉、變異操作 交叉概率Pm=0.8，變異概率滿足如下式子：

(17)

步驟5：種群個體的模擬遺傳退火算法 在種群中每一個解S的鄰域中隨機產生新解S′，并計算原來解g(s)和新解g(s′)的適應度函數，并以下述概率判斷是否接受s′作為新解：

(18)

步驟6：降溫處理 對模擬遺傳退火算法進行退溫操作，退溫操作一般采用指數退溫方法，其中λ為退溫速率，即:

T(k+1)=λT(k) 0<λ<1

(19)

在模擬遺傳退火算法參數優化過程中，設置本研究需要優化的參數向量為：

S=[b1b2b3c11c12c13

c21c22c23v1v2v3]

假設選擇的閾值的取值范圍為bj∈(0,3)、中心寬度cij∈(-5,5)、和權值函數vj∈(-1,1)，因此隨機產生50組優化參數作為算法的初始值進行尋優操作，同時將式(8)作為參數優化的目標函數，最終由算法可得到參數的最優值為如下：

S=[0.764 1.962 2.802 -2.079 -0.731

-1.757 2.818 2.572 2.138 -0.738

-0.636 -0.560]

迭代過程中的目標函數x的變化如圖5所示。

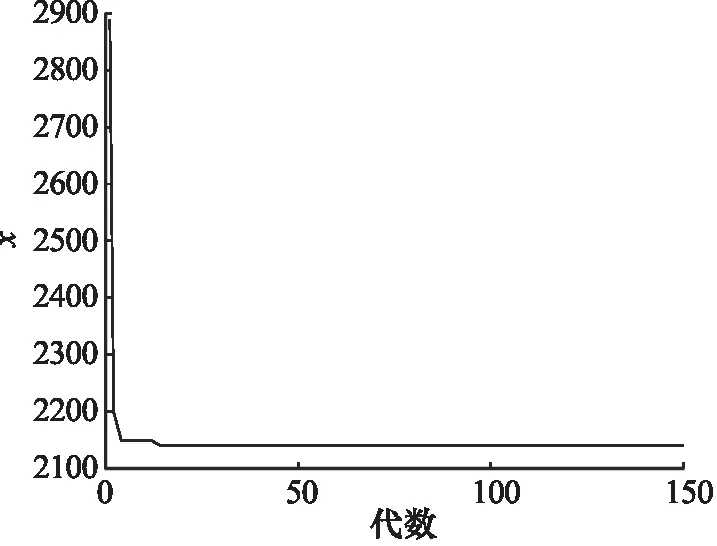
圖5 模擬遺傳算法優化過程

4 仿真研究

根據連續回轉馬達電液伺服系統的模糊RBF神經網絡控制的原理，建立其原理方框圖，如圖6所示。

圖6 模糊RBF神經網絡原理圖

連續回轉馬達電液伺服系統的仿真轉臺對性能要求苛刻，一般采用雙十指標作為量化標準，要求系統的響應幅值誤差不超過10%，相位滯后誤差不超過10°。采用頻率為10, 12, 13 Hz的正弦信號作為輸入，分別對比仿真PID控制、模糊RBF神經網絡控制作用下的響應曲線，如圖7～圖9所示。其中，圖7a、圖8a、圖9a為系統控制響應曲線，圖7b、圖8b、圖9b為曲線的局部放大圖，實線代表不同頻率下的正弦輸入信號；點劃線是傳統PID控制下的輸出響應曲線；虛線為模糊RBF神經網絡控制作用下的輸出響應曲線。

通過仿真連續回轉馬達電液伺服系統分別在頻率為10,12,13Hz的正弦輸入下系統的頻率響應，仿真結果的具體量化指標如表1、表2所示。從表中可知，隨著輸入信號頻率的增加控制效果逐漸變差，在10 Hz，12 Hz 時本研究所設計的控制器，其響應特性曲線均能滿足雙十指標的要求(即輸出信號較原始輸入信號的幅值誤差不超過10%，相位滯后不超過10°)，且很好的控制了超調現象。PID控制器作用下的正弦信號幅值誤差較小且較穩定，但相位誤差有增加趨勢，且傳統PID控制在10 Hz的控制效果已不能滿足雙十指標。

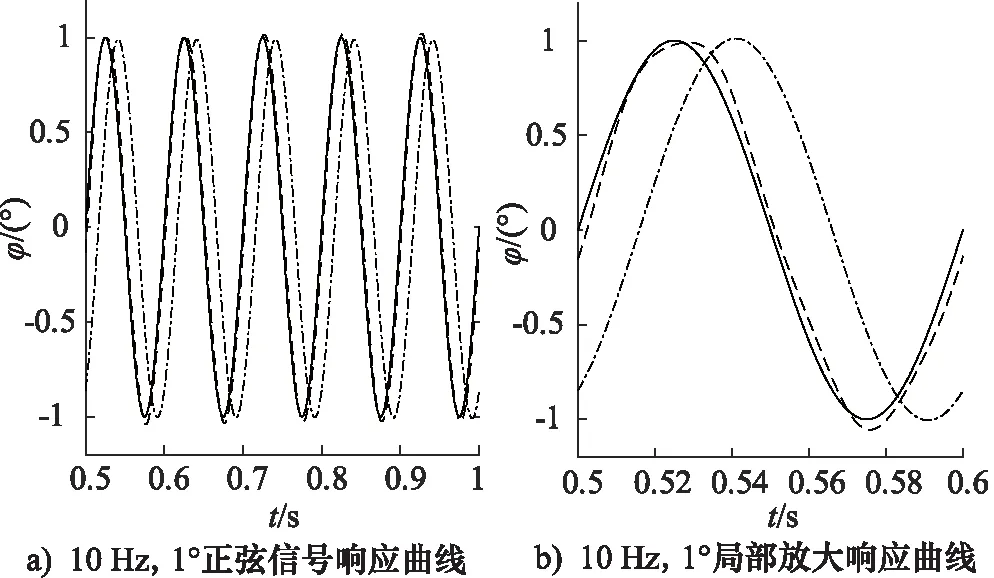
圖7 正弦輸入信號的響應特性曲線

圖8 正弦輸入信號的響應特性曲線

圖9 正弦輸入信號的響應特性曲線

表1 PID控制在幅值為1°正弦信號的跟蹤性能

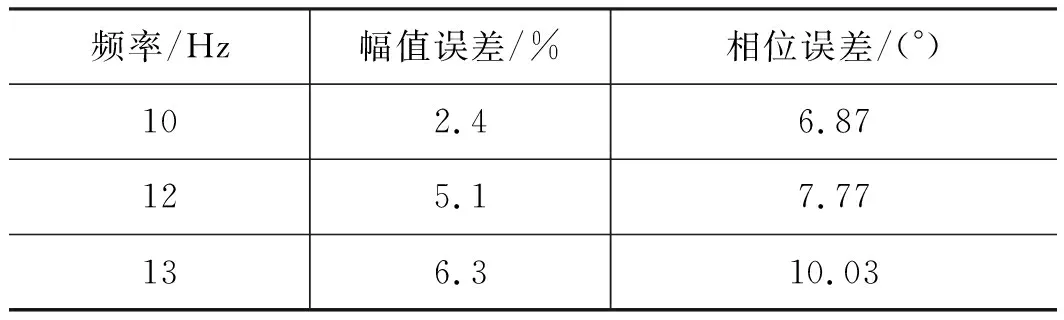
表2 模糊RBF神經網絡控制在幅值為1°正弦信號的跟蹤性能

5 結論

針對仿真轉臺用連續回轉馬達電液伺服系統中存在參數攝動和外界干擾等不確定性因素，設計了模糊RBF神經網絡控制算法，并利用模擬遺傳退火算法優化神經網絡的內部參數即閾值、中心寬度以及權值函數，從而獲得最優的模型參數，以提高控制算法的收斂速度和收斂精度。與傳統PID控制策略進行對比仿真，證明了本研究設計的控制算法對正弦響應輸入具有較好的跟蹤性能，且其響應頻率最高可達到12 Hz，拓寬了系統的頻帶，證明了控制算法的可行性和正確性。