動態生成下的高中數學概念教學

江蘇省泰州市姜堰區羅塘高級中學 王紅明

高中數學涉及很多的概念，包括向量、函數、數列、導數等，這些概念是學習高中數學知識的重要基礎。教學中為使學生牢固掌握、深入理解高中數學相關概念，促進概念教學質量的進一步提升，應注重采取高效的教學方法。其中在動態生成下，能很好地激發學生的學習積極性，使學生參與到數學概念形成中，加深其印象的同時，有助于其更好地理解與掌握。動態生成是指教師與學生、學生與學生相互合作、探究、對話實現新知識的生成。教學中應提高認識，靈活采用多種方法在動態生成下開展概念教學工作。

一、借助熟悉知識進行動態生成

向量是高中數學的重要概念，指既有大小又有方向的量，分為零向量、單位向量、相等向量、平行向量等。高中數學教學中為使學生更好地掌握向量概念，可從學生熟悉的知識切入教學，更好地吸引學生的注意力，激發其思考熱情。眾所周知，學生在初中階段已經學習過有關力的示意圖，課堂上要求學生回顧力的示意圖的三要素以及畫法，然后告知學生力的示意圖實質上就是一種向量，在此基礎上要求學生回顧所學，討論以下問題：

（1）向量和數量有什么區別與聯系？（2）如何表示向量的大小與方向？（3）向量與有向線段有什么區別？

學生在課堂上通過學習教材內容并與其他學生積極討論，對向量的概念有了全新認識，得知可用表示向量線段的長度表示向量的大小，用有向線段的箭頭表示向量的方向。學生通過學習掌握了兩個特殊的向量：單位向量、零向量。其中模為1 的向量為單位向量，其方向不受限制；零向量的長度為0，方向是任意的。另外，為獲得預期的動態生成效果，順利完成教學目標，可在課堂上為學生展示如下習題，要求學生進行作答，進一步深化其理解，更好地掌握向量這一重要的概念：

給出下列四個命題：①若a=b 都是單位向量，則a=b；②零向量的長度為零，方向是任意的；③若a=b，b=c，則a=c；④若 a∥b，b∥c，則 a∥c；則正確的命題為（ ）。

A.①② B.①④ C.②③ D.③④

對于①，單位向量是模為1 的向量，并沒有說明其方向，因此并不能判斷兩個單位向量是相等的；對于②零向量為長度為零的向量且方向不確定；對于③兩個向量相等需要模與方向均相等；對于④零向量與任意不為零的向量平行，b 為零向量時不成立。綜上可知只有②③正確，正確選項為C。

二、通過自主學習進行動態生成

學生對函數并不陌生。在初中階段已較為系統地學習過一次函數、二次函數、反比例函數等，但高中階段對函數重新進行了定義，而且涉及的內容較為抽象，學習難度較大。為使學生牢固掌握、深入理解函數這一概念，應注重鼓勵學生開展自主學習活動，通過動態生成鼓勵學生自己進行歸納、總結，在其頭腦中留下深刻的印象。一方面，圍繞函數概念認真編寫導學案，明確學生自主學習的目標、步驟、要求等，在課堂上分發給學生，必要情況下還可錄制一些微課視頻，在課堂上播放給學生觀看。另一方面，專門留出一定的時間，鼓勵學生相互交流學習心得，最終在教師的引導與啟發下，學生順利總結出了函數的概念。

學生通過自主學習參與到函數概念的動態生成過程中，從集合角度更加深刻的認識了函數的定義域、值域、對應關系三要素，而且學會了函數的表示方法，很好地增強了學生學習的自信。為使學生更好地理解函數的三要素，課堂上可向學生展示如下習題，要求學生根據自己的理解進行判斷，并說出判斷理由。

判斷下列對應關系是否為集合A 到集合B 的函數：①A=R，B={x|x＞0}，f：x→y=|x|；②A=Z，B=Z，f：x→y=x2；③④A={-1，1}，B={0}，f：x→y=0；

該題目重點考查了對函數概念的理解程度。分析時需要學生認真回顧函數的概念，牢牢把握函數概念中的一些關鍵詞，如非空集合、對應關系、任何一個等。對于①，集合A 中的元素0，在集合B 中無法找到對象，不是函數；由函數概念可知②是函數。③不是函數，如集合A 中的2 這個元素，無法在集合B 中找到對象。④為函數。

三、借助課堂互動進行動態生成

數列是高中數學重要組成部分，包括很多概念，如數列、項、通項公式等，其中數列概念本身并不難記憶與掌握，指按一定的次序排列的比系列數。但要想應用數列中的一些概念，靈活解答相關習題并非易事。其中通項公式在數列中占有重要地位，教學中為使學生能夠深刻理解，并能靈活求解數列的通項公式，應通過課堂互動在動態生成下完成教學工作。

課堂上可圍繞以下問題學生進行互動：（1）數列有哪些表示方法？（2）怎樣用解析式進行表示？（3）數列項公式描述的是誰和誰的關系？（3）怎樣求解數列的通項公式？

學生積極回答教師的問題，課堂氣氛變得十分活躍，提升了學生的學習體驗。在回答問題過程中，學生逐漸認識與掌握了數列通項公式這一概念，但一些學生不知道怎樣求解通項公式。課堂上圍繞某一具體的數列，繼續與學生互動，并為圍繞一下例題，為學生示范求解數列通項公式的具體過程，最終學生掌握了求解數列通項公式的一般思路與方法：

已知數列{an}的前n 項和Sn=2n2-3n，則數列{an}的通項公式an=______；若其前n 項和Sn=3n+1，則數列{an}的通項公式an=_____。

所謂數列通項公式是指表示數列第n 項an 和n 之間的關系的公式。根據通項公式求解方法可知，當數列的前n 項和為 Sn=2n2-3n 時，當 n=1，a1=S1=2-3=-1；當 n≥2 時，an=Sn-Sn-1=（2n2-3n）-【2（n-1）2-3（n-1）】=4n-4，a1也適合上式，其通項公式an=4n-5；當數列的前n 項和為Sn=3n+1時 ， 當 n=1，a1=S1=3+1=4； 當 n ≥2 時 ，an=Sn-Sn-1=3n+1-3n-1-1=2·3n-1，當 n=1 時不適合上式，因此，通項公式

四、借助問題情境進行動態生成

導數是高中數學的重要概念，是各類測試考查的重要知識點。教學中為使學生深入的理解導數概念，并能靈活運用，可創設學生熟悉的問題情境，通過動態生成完成這一概念的教學。

考慮學生已學的物理知識，創設以下問題情境，要求學生思考、作答：已知自由落體運動方程為S=gt2，求落體在t0到t0+△t 這段時間內的平均速度以及在t0時的瞬時速度。根據所學的物理知識，學生不難求出落體在該時間短內的平均速度，而瞬時速度為在 t0→0 的極限，顯然在t0的瞬時速度v=gt0。從函數角度來看，瞬時速度就是位移函數對時間的瞬時變化率，即函數y=f（x）在x=x0處的瞬時變化率，即為函數y=f（x）在x=x0處的導數。

教學中通過創設學生熟悉的問題情境進行動態生成，學生不僅掌握了導數的概念，而且對其導數概念的理解更為深入，尤其為鞏固學生所學，課堂上要求學生思考、解答以下習題，結果學生成功得出正確結果，順利完成了教學目標：

如下圖所示，函數f（x）的圖像是折線ABC，其中A、B、C 的坐標分別為（0，4）、（2，0）、（6，4），那么

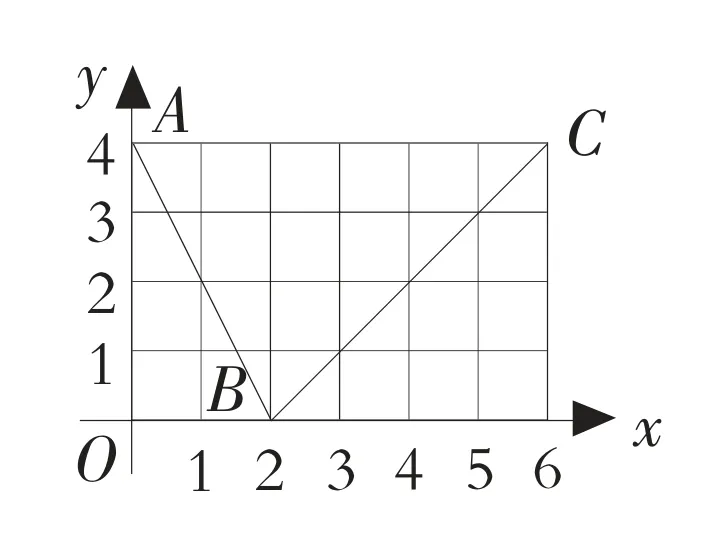
A.1 B.2 C.3 D.4

該題目靈活考查了導數的概念，只有深入理解導數表示的幾何含義，才能順利求解出該題。很多學生粗心大意，錯誤的選擇了B 項。事實上，題目要求的是函數y=f（x）在x=x0處的瞬時變化率，即為函數在x=x0處的導數。根據其定義可知題目中要求的并不是在x=3 處的導數，需將其拼湊成在 x=3 處的導數求解，即正確選項為B。

高中數學概念教學中注重動態生成，不僅能很好地提高學生的學習體驗，而且能給學生留下深刻的印象，使其更好地掌握訴求概念本質，因此教學中應提高認識，注重相關理論學習，并結合自身教學經驗積極組織學生開展動態生成下的概念教學活動，尤其應做好教學效果的總結，精益求精，對相關的教學細節進行適當的優化與調整，使學生在輕松、歡快的課堂氛圍中完成數學概念的學習。