基于改進灰狼優化算法的積分計算實驗

黃基誕

（1.東華大學旭日工商管理學院，上海 200051）

0 引言

科學計算和工程技術領域中，存在著各種數值積分的計算問題，比如橋梁設計、船舶設計、土地測繪等。目前，在數學領域中求解數值積分的方法有很多，經典的數值積分方法有牛頓-柯特斯公式（Newton-Cotes）法，辛普森求積公式（Simpson）法、梯形法、龍貝格求積公式（Romberg）、Gauss 法等［1］。但這些經典的方法在工程計算中都存在各自的不足，比如Romberg 雖計算精度高，但計算量大；Newton-Cotes 公式穩定性較差，收斂性得不到保證。近年來，隨著計算機技術的飛速發展和許多新型的智能算法的出現，有學者開始逐漸利用或結合新型群智能算法求解數值積分，并取得了良好的效果。如人工魚群算法［2］、粒子群算法［3］、細菌覓食算法［4］、差分進行算法［5-6］、蝙蝠算法［7］、神經網絡算法［8］和生物地理優化算法［9］求解任意函數的數值積分，取得了較好的效果。

上述智能算法都在一定程度上解決了經典數值積分方法的不足，取得了較大的成功，為后續學者更深入的數值研究打下了扎實的理論基礎。同時，目前國內外對群智能算法在求積分的數值解方面的研究屬于起步階段。本文將在前人的研究基礎上繼續深入拓展，改進灰狼算法用于求解數值定積分的方法，提出了結合Simpson3／8 公式的基于灰狼優化算法求任意函數的數值積分的方法。該方法的基本思路是：先在積分區間內產生一些隨機分割點（不一定是等距分割點），然后用灰狼優化算法對這些分割點進行優化，將優化后得到的最優分割點從小到大排序并作為該區間的分割點，這些分割點結合Simpson3／8 積分公式進行數值計算，在這點上與以往的智能算法求解數值積分不同，以往的這些文獻中的算法都是用的梯形公式；用本文方法求得數值積分不僅計算精度高，且對特殊函數如振蕩函數同樣適用。

隨著科技的發展及新問題的不斷出現，近些年涌現出一批新型的算法，如生物地理優化算法［9］，煙花算法［10］、引力搜索算法［11］等。這些算法優點就是能夠快捷地給出接近最優的解.灰狼算法（Grey Wolf Optimization，GWO）最早是由Mirjalili等［12］于2014 年提出的，它是模擬自然界中灰狼群社會等級和狩獵行為的一種新型群體智能優化算法。該算法通過模擬灰狼跟蹤、包圍、追捕及攻擊獵物等形式實現優化目的。灰狼算法具有數學模型簡單、全局搜索能力強、參數設置少等優點，目前逐漸在調度領域得到應用［13-14］，背包計算問題［15］；還有學者將它用于光伏陣列局部陰影下最大功率點跟蹤［16］。本文將對該算法的應用進行改進，將其用于求數值積分計算實驗。

1 基本灰狼優化算法

GWO是通過數學模型模擬生物界中狼群捕獵機制與領導結構提出的一種新型群智能搜索方法。在灰狼種群中，根據領導地位和結構由高到低分級為：頭領狼α，副頭領狼β，普通平民狼δ，底層狼ω。該狼群群等級越低，則灰狼個體數量越多。狼群體在捕獲獵物時，其他灰狼個體在頭狼α 的帶領下對獵物進行圍攻。在d 維搜索空間中，第i只灰狼的位置記：

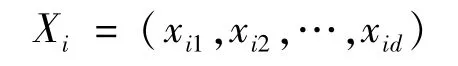
獵物的位置對應于優化問題的全局最優解。狼群獵食行動包括以下兩個主要步驟：

（1）追蹤及包圍獵物。描述灰狼追蹤并包圍獵物的行為，滿足如下公式：

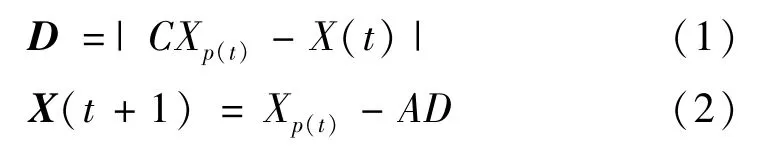
式中：t表示當前迭代次數；X（t）表示第t 代灰狼個體的位置；Xp（t）為第t 代獵物位置，常數C 是擺動因子；常數A是收斂因子

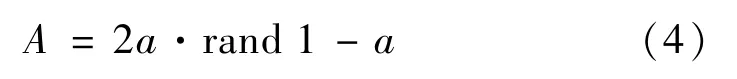
rand1，rand2 表示［0，1］之間的隨機變量；變量a 稱為隨機因子，隨迭代次數的增大從2 線性減小到0，數學表達為

（2）攻擊獵物。當灰狼判斷出獵物所在位置時，通常由頭狼α引領β和δ發動捕獵攻擊。因此狼群可以根據α、β、δ 三者的位置判斷出獵物所在方向，進而更新灰狼位置：

式中：C1，C2，C3表示一個隨機向量；X（t）表示當前灰狼位置向量。式（6）和（7）定義了ω狼朝向α，β，δ狼前進的步長和方向。然后由式（8）即可判斷出個體向獵物移動的方向和ω 狼的最終位置［12］。盡管GWO算法得到了工程領域的廣泛應用，但它和其他許多智能算法一樣存在一些不足之處，比如求解精度低、易早熟等。

2 改進GWO求解數值積分

2.1 混沌種群初始化

GWO算法產生初始種群時是隨機的，不一定均勻隨機，故可能會影響種群的多樣性。混沌序列是一種確定系統里經常出現的無規則雜亂運動，具有較強的遍歷性，通常表現為隨機情形下背后的簡單規律。根據文獻［17］中立方映射比Logistic和Tent映射產生的混沌變量更加均勻分布于區域之間，故本文采用立方映射產生混沌變量，應用于算法混沌初始化，即：

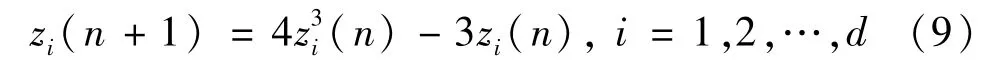
式中：－1 ≤zi（n）≤1，zi（n）≠0，n為迭代次數。由于混沌變量－1≤zi（n）≤1，zi（n）≠0，故需轉換為改進混沌GWO 中第i 個灰狼每個維度的決策變量j位置。

為提高算法的全局搜索能力，提出混沌策略改進GWO，利用混沌動力學對算法的初始化過程進行改進。同時，為進一步提高種群的多樣性，混沌序列產生初始序列的方式如下：

（1）隨機產生N 個數據點zi（1），其中i ＝1，2，…，N，N為種群數量；每個分量的值為［－1，1］之間的隨機數。

（2）分別以這些數據點為初始點按式（9）的混沌映射方式進行迭代，得到N 個混沌序列zi＝（zi（1），zi（2），…，zi（d）），d為問題維數。

（3）由于立方映射產生的序列中zi（d）的取值在－1 和1 之間，所以必須將其映射到灰狼的搜索區間中，映射規則如下：

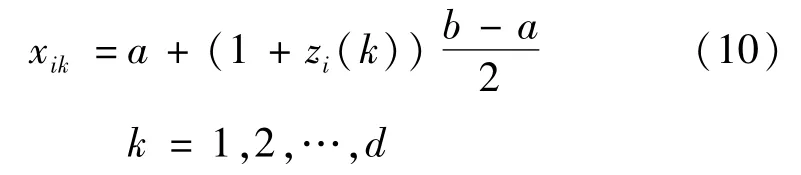
式中：a和b分別表示搜索空間第d 維的上、下限，也就是積分區間。zi（d）是利用式（10）產生的第i 個粒子的第d維，則xik即為第i個灰狼在搜索空間第k 維的坐標。

2.2 單純形差分擾動策略

為了提高GWO 的搜索性能，本文引入單純形法策略進行擾動。在一次迭代完成之后，利用單純形法搜索策略，選擇底層ω 狼進行優化。找出最優點、次優點以及最差點，通過反射、壓縮、擴張等操作更新最差點，形成一個新的多面體。它是一種局域的搜索方法。假設底層狼的位置為Xs，最優位置中心。

（1）反射操作

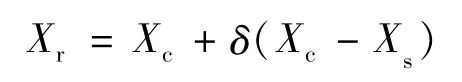
Xr為反射點，反射系數δ通常取1。

（2）擴張操作

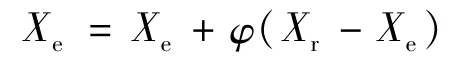
Xe為擴張點，擴張系數φ通常取2。

（3）壓縮操作

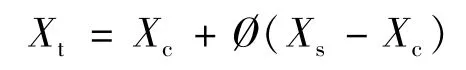
Xt為壓縮點，壓縮系數?通常取0.5。

（4）收縮操作

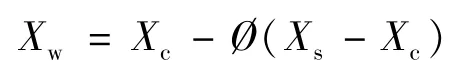
Xw為收縮點，收縮系數與壓縮系數相同。

（5）差分進化算法特點收斂速度快、探索能力強，可以使新解朝著最優的方向進行搜索。差分操作如下：

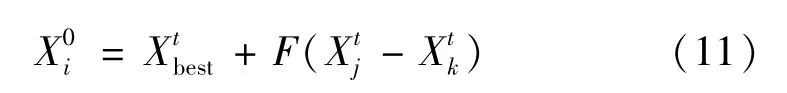
具體的單純形差分擾動策略步驟設計如下：選取任意一個底層ω 狼的位置為Xs，分別計算出Xc，Xr，；比較這些目標函數值，并選取單純形中的最優值與當前最優目標值進行比較。如果單純形中的值更優，則替換X*。

2.3 改進GWO求任意函數數值積分

綜上所述，本文提出的基于GWO 求任意函數數值積分算法流程可歸結如下：

Step 1初始化基本參數a，A 和C、NP為種群個數、問題維數d 和最大迭代次數Tmax等參數；在被積區間內［a，b］根據混沌策略生成初始種群X ＝（X1，X2，…，XN），其中：Xi＝（Xi1，Xi2，…，Xin）；Xik∈［a，b］表示第k個節點，n表示積分區間內的節點數。

Step 2計算適應度并進行排序。先將隨機產生的每個個體置于積分區間的左右端點之間，并按照升序排列，這樣就得到n ＋2 個節點和n ＋1 小段，再分別計算這n ＋2 個節點相鄰節點之間的距離dj，j ＝1，2，…，n ＋1 及這n ＋2 個節點對應的函數值和每小段中點對應的函數值，確定每小段左右端點和中間點的3個函數值中，記下最大函數值max Yj、最小函數值min Yj，j ＝1，2，…，n ＋1.并定義適應度為［7］

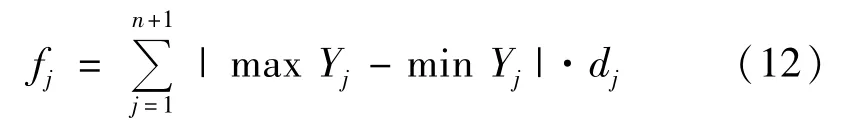
越小表明分割方法越好。

Step 3根據計算的適應度，得到當前的歷史最優解Xα，次最優解Xβ，第3 最優解Xα和ω普通狼。

Step 4由式（6）計算群體中其他灰狼個體分別與α、β、δ狼的距離，并根據式（7）、（8）更新每個灰狼個體的位置。重新計算所有個體狼的適應度值并進行排序，更新最優值前3 的灰狼個體Xα、Xβ、Xδ的位置。

Step 5對底層狼ω 實施單純形差分擾動策略，計算擾動后灰狼的適應度值并進行排序，若有改進重新找出3 個灰狼個體Xα、β、δ個體。

Step 6更新α、A和C等參數的值。

Step 7若未達到最大迭代次數Tmax，則返回步驟4；否則，輸出全局最優位置；返回最優灰狼個體位置Xα，算法結束。

Step 8計算定積分值。將所求的最優分割點［α，x1，…，Xn，b］分別代入數值積分式進行計算（a ＝x0，b ＝xn＋1），得出：

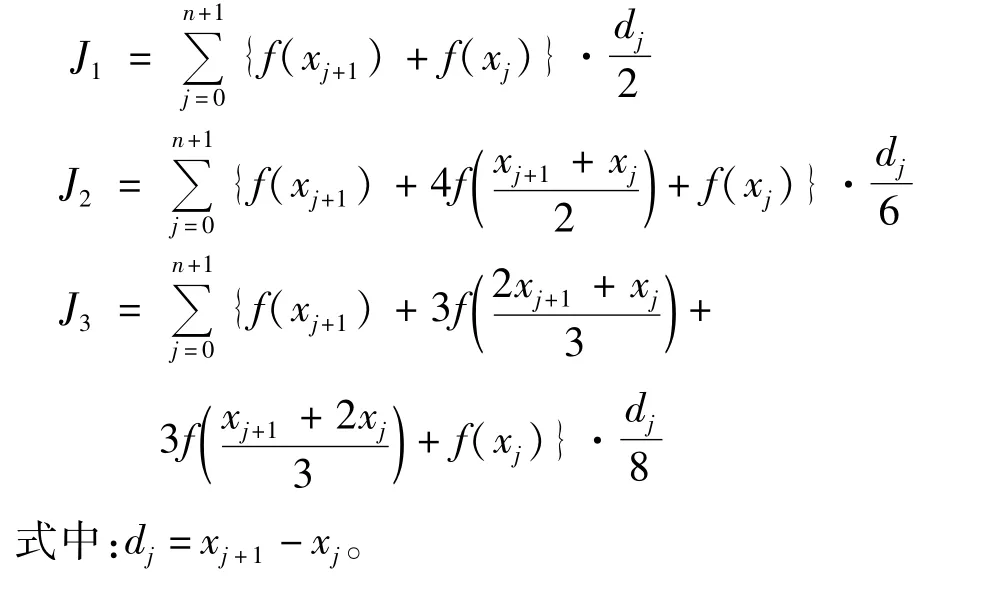
3 數值實驗

為了驗證本文提出算法的有效性和正確性，選取了幾個典型的數值積分函數，其中包括振蕩函數，并著重與文獻［6-7］中的方法進行比較。其中算法采用Matlab2015a 編程，實驗運行環境為：CPU 2.6 GHz，內存4 GB，Windows7 操作系統（64 位）。

例1計算積分

該函數積分精確值為58.470 469 1［6-7］。文獻［6］中給出用差分優化算法計算的結果值58.470 517 8；文獻［7］中給出用蝙蝠優化算法計算的結果值為58.470 821 5；本文取N ＝15，D ＝100，運用灰狼優化算法計算結果為：

例2取N ＝20，D ＝60，分別計算6 個函數：x2，在積分區間［0，2］內的積分（見表1）。

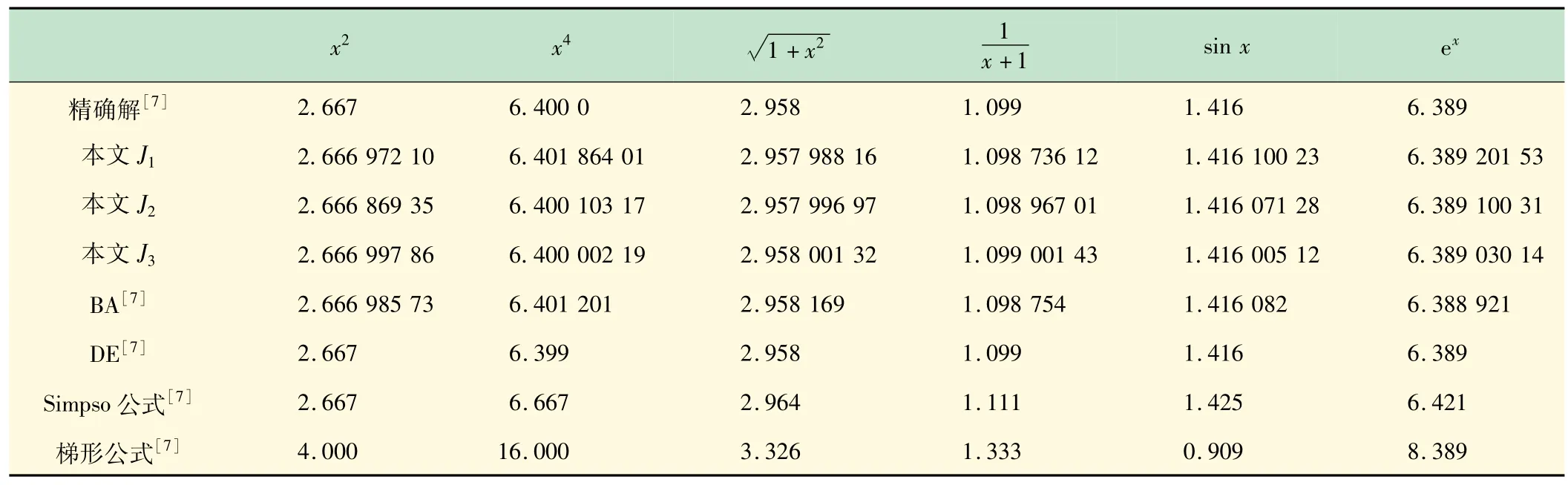
表1 各算法對例2 的函數積分值比較

例3計算振蕩函數積

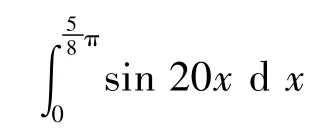
該振蕩函數積分的精確值為0.05［7］。文獻［7］中給出的用蝙蝠優化算法計算的結果值為

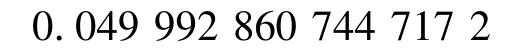
本文取N ＝20，D ＝120。運用灰狼優化算法計算結果：

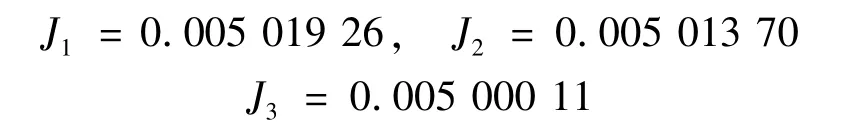
例4計算振蕩函數積

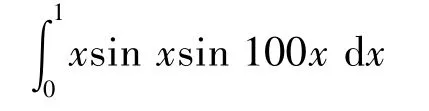
該振蕩函數積分的精確值為－0.007 327 9［7］。文獻［6］中給出的用差分優化算法計算的結果值為－0.007 332 8；文獻［7］中給出的用蝙蝠優化算法計算的結果值為－0.007 335 411 855 213 67；采用本文灰狼優化算法時，針對被積函數的振蕩性特點，分割點n取為200，其他參數設置不變。本文計算結果為：

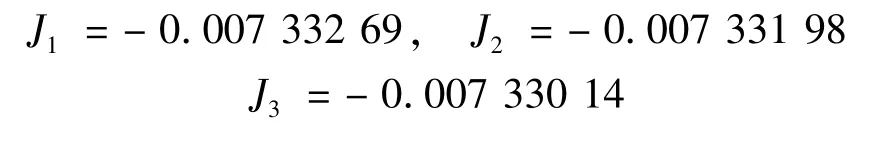
4 結語

本文提出了用單純形擾動和混沌映射方法改進灰狼優化算法結合Simpson3／8 積分求函數數值積分，對4 個不同數值積分算例進行測試。仿真結果表明，該算法收斂性、計算精度相比經典的數值積分方法優勢比較明顯，驗證了灰狼優化算法改進的有效性和可行性。不僅對常用函數進行積分，還可以計算振蕩積分等特殊情形，此方法是對經典求積分數值方法的一種有效補充。同時，也可作為灰狼優化算法應用領域的拓展應用。如何利用改進灰狼算法進行二重積分和三重積分計算，甚至利用灰狼優化算法計算常微分方程的數值解等問題可作為今后進一步研究的內容和方向。