單源點疏散問題的Online探索算法研究

胡秀婷，謝玉瑩，包敏澤，蔣 波，楊玉晗

1(大連海事大學 信息科學技術學院，遼寧 大連 116026) 2(華為技術有限公司 華為北京研究所，北京 100000)

1 問題描述

本文研究的問題是關于單源點疏散問題的online快速撤離算法.所謂單源點疏散問題，簡稱“單源點問題”，是指受災人員位于危險區域中的同一位置，需要快速地撤離出該區域并到達安全區域.由于危險區域的邊界(安全區域)對受災人員而言往往是未知的，所以受災人員需要采取某種策略探索出安全邊界.一般而言，稱邊界信息未知的一類搜索問題為online探索問題，而邊界信息已知的搜索問題則稱為offline搜索問題.由于缺乏邊界信息的引導，使得online探索問題相對于一般搜索問題而言要復雜很多.近年來，人們提出了很多疏散問題的撤離策略，本文的研究目標是設計出一個更為高效的探索危險區域安全邊界的撤離算法.

為了衡量撤離算法的效率，人們提出了競爭比的概念.所謂競爭比，是指online探索策略所花費的代價與該問題在邊界信息已知情形下所設計出的最優搜索策略(offline搜索策略)的代價之比.顯然，所謂“快速”或“好”的online探索策略是指競爭比較小的求解方法.探索策略的代價可用耗費的時間或路徑長度來衡量，因為求解這類問題時的移動速度一般都假設是勻速的.

本文研究單源點疏散問題，將受災人員分為1組或多組，分別提出了三角形疏散策略和半圓疏散策略，以降低撤離算法的競爭比，提升撤離算法的效率，同時解決了受災區域為非凸多邊形的單源點疏散問題.

2 單源點疏散問題的探索策略

針對單源點疏散問題的研究，約定如下：

1)對1組疏散問題，將受災區域的邊界設定為凸多邊形；

2)受災人員的撤離速度是相同的；

3)受災區域的邊界與受災人員的初始位置是未知的，但在疏散過程中，受災人員之間可以相互通信，共享位置信息；

4)在疏散過程中，當其中一組受災人員探索到未知區域邊界時，其余組人員可以獲得該信息并立即(沒有時間延誤)改變疏散方向，朝著已發現的邊界移動.

假設將危險區域記為P，它是一個簡單多邊形.受災人員在P中的初始位置記為O，點m與點n間的線段長度記為|mn|，Dopt表示最優的offline路徑長度，S(m，n)表示m點與n點之間的路徑.競爭比記為k，可通過公式(1)計算：

(1)

其中，Sonline表示online探索的路徑長度；Soffline表示offline搜索的路徑長度.

2.1 單源點單組三角形疏散策略

假設受災人員首先沿橫坐標向右移動單位長度d，然后按逆時針方向旋轉45°，繼續移動長度d，接著再按逆時針方向旋轉108°18′，并移動d，這時受災人員又到達了橫坐標上，完成了一次三角曲線移動(從橫坐標軸到橫坐標軸，并做了兩次旋轉).接著，按逆時針方向旋轉71°42′(與橫坐標軸的夾角為45°)，并移動2d，再按逆時針方向旋轉108°18′，并移動2d，又一次回到橫坐標軸并完成了第2次三角曲線移動.重復這個過程，直到發現P的邊界.

一個三角曲線移動的示例如圖1所示.由于∠ODA=45°，若|OC|=|OD|，則∠CAD為直角.在OC延長線上確定點B，使得|OC|=|BC|，則有|OB|=2*|OD|，且∠CAB=18°18′，所以在點A處旋轉108°18′的目的是構造|OB|=2*|OD|的移動策略，以便計算移動路徑的長度.由于移動過程中按照逆時針方向旋轉了兩次，所以移動路線與水平方向上呈三角形形狀，故稱其為三角形疏散策略.

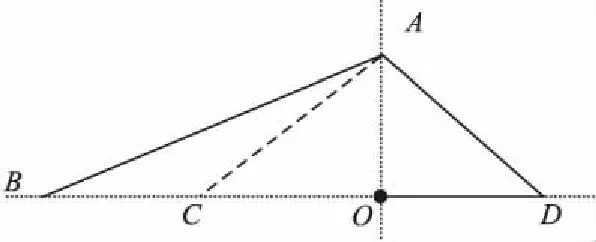
圖1 三角曲線移動的示例Fig.1 Instance of moving in trigonometric curve

由于第i項是第i-1項長度的2倍(i≥2)，所以三角形策略實際上是“雙倍策略”[6]在平面上的拓展應用，受災人員移動的路線在平面上可以看成是一個個三角形.受災人員的疏散過程如圖2所示.

圖2 三角形疏散策略的移動過程Fig.2 Moving process of triangle evacuation strategies

為計算疏散策略的競爭比，需要分析相應策略在最壞情形下的移動路徑程度，以及在邊界信息已知情形下的最短移動路徑，即Soffline.如圖2所示，online情形的最壞情形是：上一次三角曲線移動已經很接近P的邊界，但沒有碰到邊界，如圖2中的粗虛線所示.進入當前三角曲線移動后，在點F處也很接近P的邊界，連接EF，從O點向P邊界做垂線，分別交線段EF和P邊界于M和D點，|OD|是O到P邊界的最短距離，即Soffline.由于受災人員在M點沒有碰到P邊界，所以有 |OM|<|OD|.又因為受災人員做第n次三角曲線移動時已經非常接近但沒有碰到P邊界，考慮到P是凸多邊形，因此最壞情形是受災人員在第n+1次三角曲線移動時仍然碰不到P邊界，但在第n+2次三角曲線移動過程中必然穿過P的邊界，如圖2中點T所示.因此，受災人員的移動路徑長度Sonline可按如下方法計算：

受災人員所走的路徑為：

(2)

其中，|N′T|表示最后一次做三角曲線移動時(沒有完成)所移動的距離，它等于第n+1次三角曲線移動的短邊長度，有：

(3)

Soffline=|OD|是邊界信息已知情形下的最短路徑，且有|OM|<|OD|，所以可計算出|OM|并用它代替Soffline計算競爭比.如圖2所示，在ΔOEF中，由于|OF|=2|OE|，所以可計算出∠OFE的角度，進而利用相似三角形的特性，可計算出|OM|長度.考慮一般情形，有：

(4)

因此有競爭比為：

上述結果表明，單源點單組三角形疏散策略的競爭比不超過19.48，它優于文獻[6]給出的競爭比為19.64的半圓疏散策略，但又比“雙倍策略”的競爭比理論下界9高出1倍多.當然，和所有單組疏散策略一樣，單組三角形疏散策略也不能很好地處理危險區域P是非凸多邊形的情形.

2.2 單源點2組半圓疏散策略

對于分組數為2的單源點疏散問題，由于兩組人員始終沿著相反的方向進行疏散，所以最終肯定會有一組人員探索到距離其最近的邊界，因此，分組數為2的單源點半圓疏散策略可以解決受災區域為非凸多邊形的疏散問題.圖3給出了簡單非凸多邊形的部分邊界.

圖3 半圓疏散策略的移動過程Fig.3 Moving process of semicircle evacuation strategies

當疏散人員被分為n(n≥2)組時，半圓搜索策略的多組人員通過由內向外疏散，其疏散路徑構成了一個圓，所以無論凹頂點出現在平面內的任意位置，總會有一組疏散人員可以發現疏散區域中凹頂點所在的邊界，圖3給出了分組數為2時的一種疏散情形.當其中一組疏散人員無限接近于Q處的凹頂點但始終未碰到邊界時，另一組人員在后續疏散過程中一定會在點T處發現該邊界.

當疏散區域邊界為非凸(凹)多邊形時，可采用與凸多邊形競爭比類似的分析方法.在分析競爭比時，使Soffline的長度盡可能小，而Sonline的長度則盡可能大，這樣計算出的競爭比才能真正體現“最壞”情形.如圖4所示，一組受災人員沿橫坐標向右移動單位長度d，然后沿逆時針方向移動一個半圓弧長，并再次到達橫坐標，完成了一次半圓移動.接著，再走一段單位長度d，并按逆時針方向移動一個半圓，又一次回到橫坐標軸上，完成了第2次半圓曲線移動,其中半圓的半徑長度采用雙倍策略遞增，并且這些半圓共用一個圓心點O.與此同時，另一組人員始終沿著與上一組人員的相反疏散方向進行疏散，直到發現凹多邊形P的邊界.當點T在S(O，B)內時，Soffline的長度接近于第一個圓的半徑時是最優的，即凹點無限接近于第一個圓周.可以看出，當T點無限接近于B點時，各組人員的疏散路徑是最長的，也即Sonline的長度最大.所以，當某組疏散人員在點B處碰到多邊形邊界(相交于點T)時，計算出的競爭比是最大的.

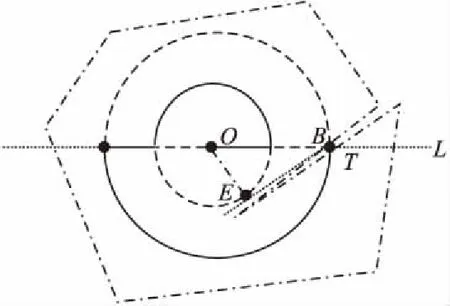
圖4 凹多邊形內分組數為2的半圓疏散策略Fig.4 Semicircle evacuation strategy with grouping of2 in concave polygon

若假設某組人員在第n+1次疏散時碰到多邊形邊界，完成疏散，則Dopt是第n個圓周的半徑長度，所以競爭比可按如下方法計算：

通過計算半圓疏散策略的競爭比計算，說明半圓策略是解決凹多邊形疏散問題的一個高效可行方法.

3 算法的實現

上述算法已通過程序實現.針對不同疏散策略，計算出不同頂點數的多邊形的探索路徑長度，并計算出競爭比，以便對比分析，如表1所示.其中(凸)與(凹)表示多邊形的形狀，P表示疏散人員所探索的不同頂點數的多邊形，即不同形狀的多邊形.

算法的有效性是通過競爭比來衡量的，競爭比越低算法越有效.關于凸多邊形的問題，文獻[14]提出了單源點單組半圓疏散算法，但本文的單源點單組三角形疏散策略卻得到了一個更低的競爭比，改進了凸多邊形情形下的疏散問題求解算法.針對非凸多邊形情形下的疏散問題，文獻[15]提出的兩組半方形疏散策略的競爭比不超過24，本文提出的兩組半圓疏散算法的競爭比則不超過18.56，與半方形疏散策略相比，半圓策略進一步改進了非凸多邊形情形的疏散算法.同時，由表1可知，在不同的多邊形疏散區域中，凸多邊形情形下的三角形策略的競爭比低于半圓策略，所以三角形疏散算法優于半圓疏散算法；非凸多邊形情形下的半圓策略競爭比低于半方形策略，所以半圓疏散算法優于半方形疏散算法.

表1 不同疏散策略的實驗結果比較Table 1 Comparison of experimental results of differentevacuation strategies

4 結 論

本文主要研究了受災區域為簡單凸多邊形和簡單非凸多邊形情形下單源點疏散問題的疏散策略，其中探索凸多邊形區域的單源點單組疏散策略的競爭比為19.48，低于單源點單組半圓疏散策略的19.64[14].由于單組疏散策略只適用于凸多邊形區域的問題求解，對于非凸多邊形的情形，必須采用多組疏散策略，為此，我們提出了單源點2組半圓疏散策略用于求解非凸多邊形的單源點疏散問題，得到了競爭比為18.56的研究結果，優于已有的撤離算法.針對單源點疏散問題的online探索算法，雖然已有一些解決方案，但仍然存在較大的改進空間，需要做進一步研究，以找出更好的疏散方法，獲得更低的競爭比，減少疏散成本并方便應用.