CPU-GPU異構平臺的拋物線Radon變換并行算法

張 全 林柏櫟 楊 勃 彭 博 張 偉 涂 然

(①西南石油大學計算機科學學院， 四川成都 610500； ②電子科技大學信息與通信工程學院， 四川成都 611731； ③國家電網重慶市電力公司電力科學研究院，重慶 404100)

0 引言

隨著油氣勘探的不斷深入，地震勘探也面臨越來越大的挑戰，勘探目標逐漸從簡單構造轉向更復雜的地質構造。在構造復雜的低信噪比地區，其發育的噪聲干擾往往會弱化或掩蓋有效波信息，導致地震資料無法準確反映地下真實地質狀況[1-2]。地震資料中的噪聲主要是面波、多次波及隨機噪聲，其中多次波的存在不僅嚴重干擾一次波的成像質量，降低成像結果信噪比，且在地震剖面上易產生構造假象，掩蓋中深部有利構造，影響地震資料的精細解釋，所以在偏移前需壓制和去除多次波[2-3]。拋物線Radon變換[4]是現今壓制多次波的常用方法。

Radon變換[5]由奧地利數學家拉東(Radon)率先提出，后被廣泛地應用于醫學、地球物理、核磁共振、天文和分子生物等領域。1971年，Claerbout等[6]將其引入地震數據處理中，奠定了Radon變換在該領域的應用基礎。Thorson等[7]將Radon建模為一個稀疏逆問題，在Radon域實現了高分辨率數據處理。隨后Scales等[8]利用迭代加權最小二乘算法求解了稀疏逆問題。Sacchi等[9]提出的頻域稀疏Radon變換方法被廣泛地應用于地震信號處理。Trad等[10]通過混合Radon變換成功地壓制了噪聲。劉喜武等[11]基于最小二乘反演法并導出稀疏約束條件下的共軛梯度算法，實現了高分辨率Radon變換。Schonewille等[12]證明了Radon變換在時域的稀疏性高于頻域，故認為Radon變換在時域具有更高分辨率。Lu[13]提出一種基于迭代收縮的快速稀疏Radon變換方法，提高了Radon模型的稀疏性。

在實際地震數據處理中，Radon變換存在分辨率低和計算效率不高兩大缺陷[14]。Radon模型分辨率的提高可減少空間假頻和假象的產生而取得更佳處理效果，但伴隨更大計算量。況且，地震勘探數據量的日益龐大，使拋物線Radon變換在地震數據處理上耗費更長時間。

隨著GPU-CPU異構結構的出現，高性能計算技術取得快速且巨大的發展，并逐漸應用于地震勘探領域。張軍華等[15]全面調研了地球物理勘探領域對高性能計算的需求和應用現狀。近年來，更有眾多學者將CPU-GPU異構并行方法應用于疊前數據處理[16-20]。本文基于CPU-GPU異構平臺，對拋物線Radon變換算法做并行化分析和實現。

1 算法原理及串行流程

1.1 算法原理

多次波的壓制通常是在做動校正后進行的。經合適的動校正后，一次波同相軸水平； 而校正不足時多次波同相軸沿拋物線軌跡分布，則可沿拋物線做Radon變換，并在Radon域壓制多次波。本文采用Lu[13]提出的拋物線Radon變換法。混合域拋物線Radon變換的數學模型表示為

d′=F-1[LF(m)]

(1)

式中：m為Radon域數據；d′為地震數據；L為頻域Radon算子； F(·)為傅里葉變換； F-1(·)為傅里葉逆變換。為了使Radon域數據盡量稀疏且Radon反變換后的數據d′與地震數據的誤差盡量小，所以最小化如下目標方程

(2)

式中λ為正則化系數。

結合迭代收縮閾值算法[21]，對目標方程最優解的求解變為迭代計算mk，即有

mk=Tα{mk-1+2tF-1[A(F(d)-LF(mk-1))]}

(3)

式中：k表示迭代次數；mk表示迭代第k次的Radon域數據；t為迭代步長；A=(LTL)-1LT為算子L的廣義逆。

迭代收縮閾值算法是在每一步迭代過程中采用

(4)

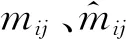
(5)

式中： ave表示二維均值濾波； max表示取最大值； |m|表示對向量m每個元素取絕對值。且有

(6)

式中α為標量。

1.2 串行算法流程

根據Lu[13]提出的一種基于迭代收縮的快速稀疏Radon變換方法的算法原理，算法實現流程如圖1所示，核心計算部分分為如下四步。

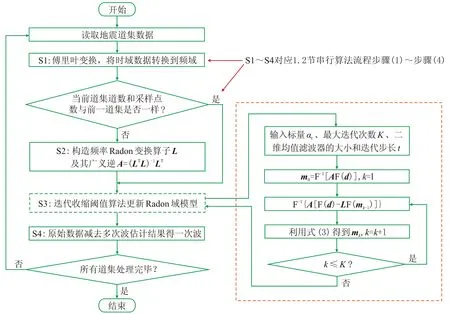
圖1 拋物線Radon變換串行算法流程

(1)首先從硬盤讀取一個地震道集數據到內存，通過傅里葉變換將地震數據從時域轉換到頻域； 然后計算頻域Radon算子L。由于此時L的計算只與地震道集的道數和采樣點數有關，所以當前道集與前一道集的道數和采樣點數相同時，不需再計算L，能直接用前一道集的計算結果，即可轉到步驟(3)； 不相同時需重新計算L，順接到步驟(2)。

(2)在頻域內構造Radon變換算子L，并計算其廣義逆A=(LTL)-1LT。

(3)基于迭代收縮閾值算法更新Radon域模型，根據步驟(2)計算結果，得到初始Radon域模型m0=F-1[AF(d)]，且k=k+1，利用式(3)得到第k次迭代的Radon域模型mk。當k≤K時，不斷更新mk。該步驟為本算法的計算熱點。

(4)設定一個曲率q，將曲率大于q的Radon域數據作為多次波估計結果，用原始地震數據減去多次波估計結果，就得到一次波。所有道集處理完畢則結束，否則轉到步驟(1)。

2 并行拋物線Radon變換算法

2.1 GPU的并行實現

首先在單個GPU上實現拋物線Radon變換算法的并行化，其流程如圖2所示。

由于CPU與GPU不能相互訪問各自存儲器，所以通過PCIE總線用拷貝方式實現數據在內存與顯存間的傳輸。首先在CPU上從硬盤讀取地震數據到內存，然后將地震數據和所需參數拷貝到GPU，在GPU端實施拋物線Radon變換，最后將計算結果拷貝到CPU，由CPU將結果從內存寫回硬盤。在GPU上實施拋物線Radon變換分為四個步驟。

(1)由于算法在頻域內實現，首先要將時域地震數據轉換到頻域，本文采用CUDA提供的快速傅里葉變換(cuFFT)實現。在后述步驟中，地震數據和Radon域數據在計算過程中仍需在頻域與時域間進行傅里葉正、逆變換，一律使用CUDA提供的cuFFT庫進行處理。cuFFT庫的使用一方面能給算法帶來性能提升，另一方面可降低程序設計復雜度，提高開發效率。值得注意的是，GPU上利用cuFFT庫計算傅里葉變換的結果與CPU上的計算結果存在一定差異，但這種差異是由于兩種不同的處理器架構在機器指令上的差異導致的，該差異與真值的比值在10-6以下，通常可忽略。

圖2 拋物線Radon變換GPU并行算法流程

(2)首先構造頻率域算子L，再計算矩陣LTL和(LTL)-1，最后計算A=(LTL)-1LT。通過調用CUDA提供的cuBLAS庫、cuSOLVER庫做線性代數運算。

(3)基于迭代收縮閾值算法更新Radon域模型。首先使用cuFFT庫和線性代數庫計算Radon初始估計模型m0=F-1[AF(d)]； 再通過式(3)進行收縮閾值操作，這時需對Radon域數據(nq×np，nq為曲率個數，np為采樣點數)進行均值濾波處理，均值濾波模板尺寸為n×m。在做均值濾波前，需先擴充Radon域數據矩陣，擴充后大小為(nq+2n)×(np+2m)。矩陣擴充后進行均值濾波，分別用兩個核函數實現，一個核函數按模板m在列方向上累加求平均值，另一個核函數按模板n在行方向上累加求平均值，最終得到均值濾波結果； 在迭代更新Radon域模型時計算A[F(d)-LF(mk-1)]，使用cuFFT庫計算傅里葉變換，使用線性代數庫計算矩陣乘法； 拋物線Radon變換算法中Radon域模型更新為迭代過程，在迭代開始前將所需數據從CPU一次拷貝到GPU，避免了迭代時CPU與GPU之間數據的傳輸，使得迭代過程可全速進行。

(4)對步驟(3)所得Radon域數據m中曲率大于q的數據作為多次波估計結果F-1[LF(m)]，通過cuFFT庫和CUDA提供的線性代數庫進行計算。最后通過d-F-1[LF(m)]得到有效波。

2.2 CPU-GPU異構平臺的協同并行實現

對于上述GPU的并行算法，在執行過程中需要主機的一個線程完成GPU核函數的調用，主機的其他線程都處于空閑狀態，勢必造成計算資源的浪費。為了充分利用多核CPU和多GPU異構計算平臺的計算資源，本文進一步提出一種協同計算方案，實現拋物線Radon變換算法。

該方案中，對于支持m個CPU線程和n個GPU的異構計算平臺，有具體的并行優化流程(圖3)。

(1)主機端主線程獲取CPU支持的線程數m，并對N個地震道集進行任務的劃分，創建一個有N個地震道集的任務隊列。

(2)每個子線程從任務隊列取一個任務執行，即每個子線程負責一個地震道集的拋物線Radon變換的計算，m個子線程并行執行m個任務。

(3)每個子線程領取一個地震道集任務后，要將該地震道集數據從硬盤讀取到內存； 然后申請CPU計算資源，若子線程成功獲取CPU計算資源，則對拋物線Radon變換算法進行預處理； 否則，子線程被阻塞，直到計算機操作系統將其調度。

(4)子線程申請GPU計算資源，若成功獲取GPU計算資源，就可調用GPU核函數完成并行拋物線Radon變換算法； 否則，調用CPU計算資源完成串行拋物線Radon變換算法。

(5)每個子線程在計算結束后將地震數據從內存寫回硬盤。最后判斷任務隊列是否為空，當任務隊列為空，則任務結束； 否則，每個線程繼續獲取任務，重復上面的操作。

本實驗中使用的CPU-GPU異構平臺由12個CPU核心和兩個GPU組成。該平臺支持CPU超線程技術，每個核心支持雙線程，所以該異構計算平臺支持24個CPU線程。在該實驗異構平臺上任務分配與執行情況如圖4所示：輸入N個地震道集，主線程創建23個子線程，然后進行任務分配并參與計算，從而實現24個線程并行執行不同道集任務。

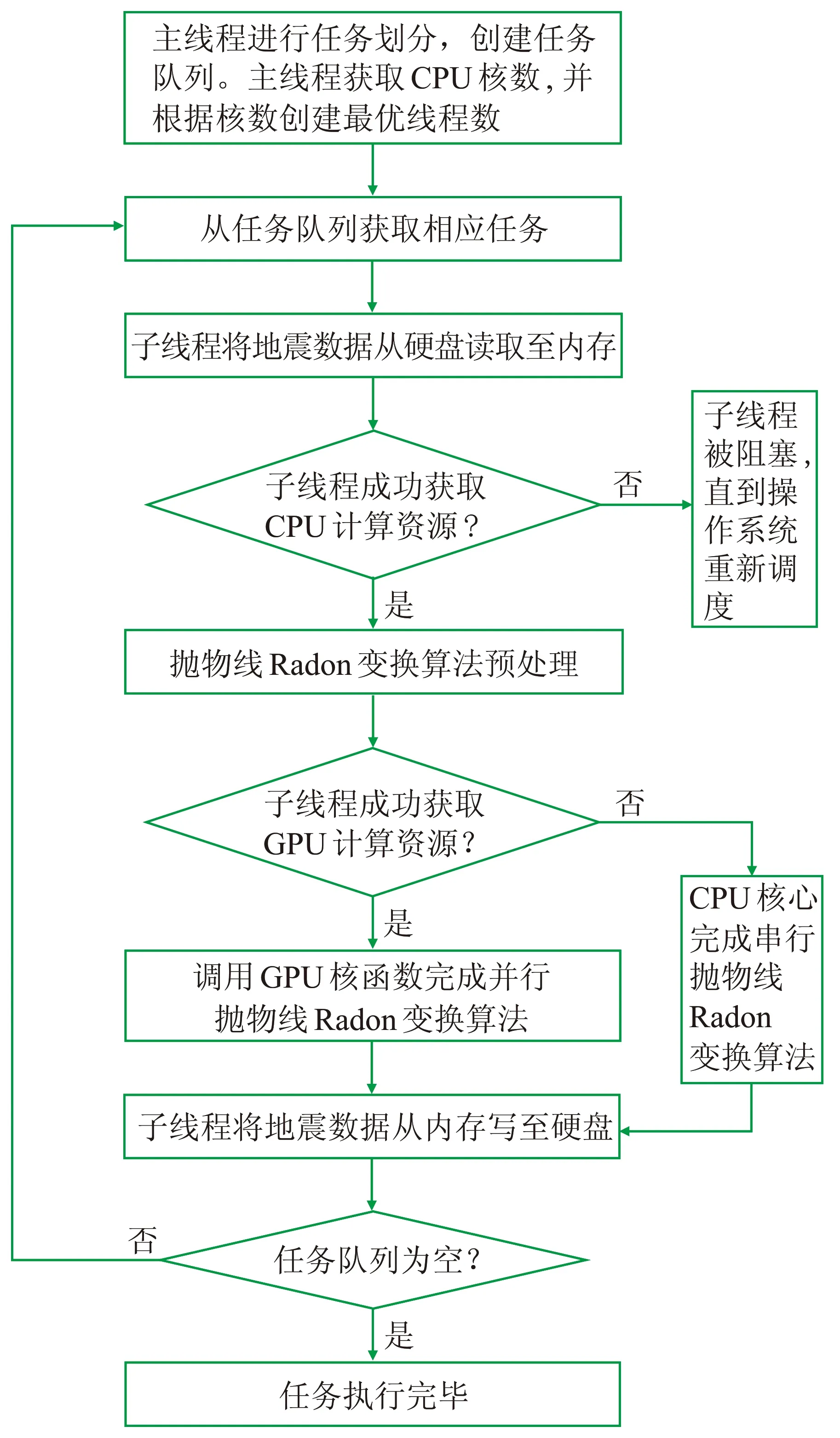
圖3 CPU-GPU異構協同并行流程

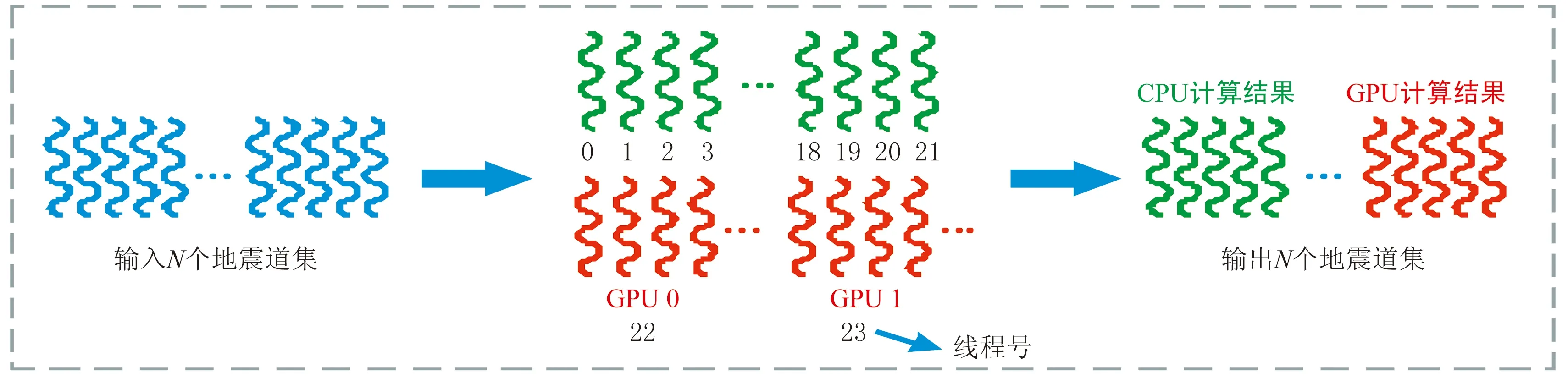
圖4 異構平臺任務分配與執行

由于該實驗平臺有兩塊GPU(GPU0和GPU1)，則由兩個CPU線程分別調用GPU0和GPU1對地震道集進行計算。因為GPU計算速度比CPU快，所以在一個CPU線程執行周期，GPU計算了多個地震道集。最終，在CPU-GPU異構計算平臺上，計算結果分別由CPU和GPU的計算結果構成。

3 數據應用

3.1 模擬數據

本文使用SeismicLab工具包中合成的CMP多次波模擬數據。該動校正后的CMP數據(圖5a)包括49道，每道有1001個采樣點。對比SeismicLab工具包中拋物線Radon變換壓制多次波的結果(圖5b)與本文方法的去噪結果(圖5c)，可見后者對多次波有更好壓制效果。

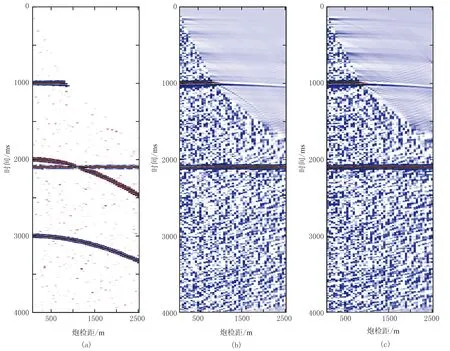
圖5 動校正后CMP道集(a)及SeismicLab拋物線Radon變換法(b)與本文算法(c)壓制多次波效果對比

3.2 實際數據

針對CPU-GPU異構平臺拋物線Radon變換算法并行優化的性能進行測試。所有測試均在表1的軟硬件環境下進行，所使用的實驗平臺有兩個CPU處理器12個核心(支持24線程)和兩塊NVIDIA Tesla K20c。

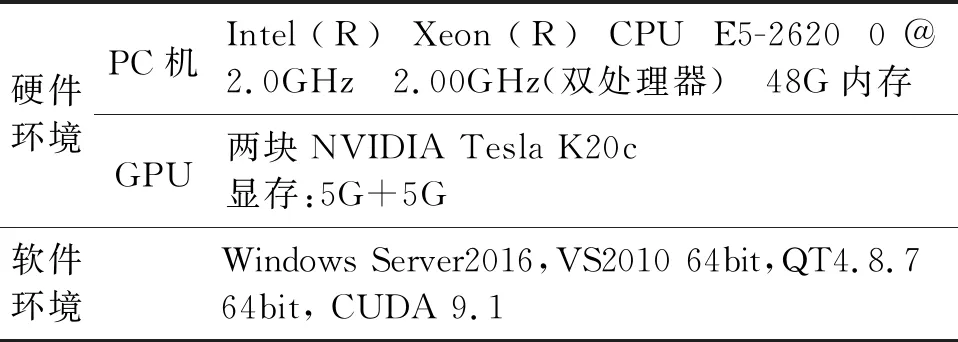
表1 軟硬件測試環境

實測數據取自珠江口盆地白云深水區。該區地形崎嶇，地層傾角較大，橫向巖性變化劇烈，地質構造復雜多變，多次波極為發育，是影響該區地震資料成像效果的主要原因[22]。實際測線范圍是： Inline2200～2300，Xline1500～1700，且每個地震道集有51道，采樣點數為376，采樣間隔為4ms。

先測試并考察算法精度，通過比較CPU串行算法與單GPU并行算法對多次波的壓制結果，驗證GPU并行結果的正確性。由于CPU-GPU并行結果是由CPU結果和GPU結果組成的，所以只需驗證GPU結果即驗證了CPU-GPU結果的正確性。選取該區某一地震道集，從其動校正后的原始道集數據(圖6a)中可看到明顯存在的多次波，在經CPU串行算法(圖6b)、單GPU并行算法(圖6c)的處理結果中，多次波已被壓制。由于乘加運算在GPU上由一條指令完成，而CPU需多條指令，從而導致計算結果有微小差異，但這種差異在高性能計算領域屬正常現象，可忽略不計[23]。

以CPU處理結果為參照，將CPU運行結果減去GPU運行結果得到兩者的計算差異(圖6d)，其范圍在10-8量級，顯然該差異可忽略不計。對比多次波壓制前(圖7a)與在CPU-GPU異構平臺上多次波壓制后(圖7b)的疊加剖面，可見后者的多次波被衰減(紅色箭頭)，層次變得清晰，使得一次波同相軸更突出。

圖6 CPU與GPU平臺上多次波去除效果

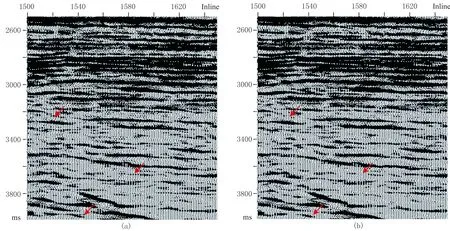
圖7 CPU-GPU異構計算平臺多次波去除前(a)、后(b)疊加剖面

在保證結果正確的前提下，再對CPU-GPU異構平臺并行加速的效果進行測試。不計數據從硬盤讀寫的時間，分別測得CPU串行、單核CPU-單GPU、12核CPU和12核CPU-雙GPU的計算耗時，其結果如表2所示。并根據本文加速比公式

(7)

分別計算不同平臺加速比。式中TR和TC對應異構平臺運行時間、串行運行時間。

圖8為三種異構平臺的加速比。分析表2和圖8可知：當地震數據范圍是Inline2200～2205、Xline1500～1510(即地震道集數為6×11)時，硬件資源未充分利用，加速比不穩定； 當地震數據范圍是Inline2200～2300、Xline1500～1700(地震道集數為101×201)時，硬件資源得到充分利用，且在密集計算時CPU利用率達到100%，GPU利用率最高達88%，加速比趨于穩定。此時單核CPU—單GPU異構平臺的加速比達到13以上；12核CPU的平臺實際加速比達到12以上；12核CPU—雙GPU的加速比也超過30。由于Windows操作系統不是實時的，會受到其他程序影響，加速比會小幅波動。

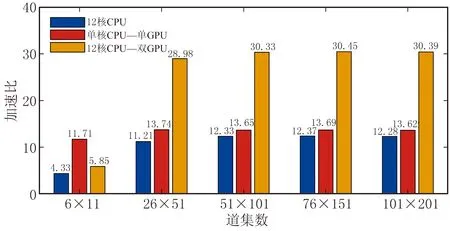
圖8 不同異構計算平臺加速比

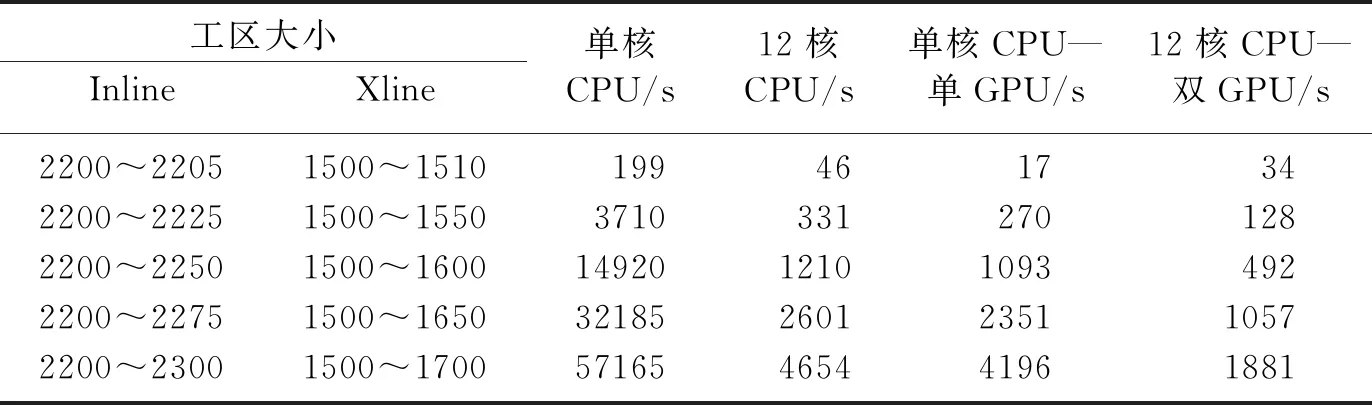
表2 不同平臺上的計算耗時

4 結束語

拋物線Radon變換算法可壓制和去除多次波，提高地震資料的信噪比。但對于數據規模巨大的地震道集，進行拋物線Radon變換需較長運行時間。為此，本文基于CPU-GPU異構平臺對拋物線Radon變換算法做并行化分析，通過CUDA優化技術在GPU平臺實施并行化，且利用多核CPU多線程技術，提出一種通用的CPU-GPU異構并行方案，充分地利用了CPU和GPU的計算資源，在保證道集質量的前提下，大幅度提高了該算法的計算效率，加速比達30。

成都晶石石油軟件有限公司在課題研究中提供了GEOSCOPE地質放大鏡軟件，在此深表感謝！