移樣離散傅里葉變換在重磁勘探中的應用

柴玉璞 萬海珍

(東方地球物理公司綜合物化探處，河北涿州 072751)

0 引言

重磁資料反演是解釋人員從重磁資料中獲取地質信息的重要手段，而絕大多數(shù)反演方法都是以正演方法為基礎構建的。因此重磁數(shù)據(jù)的正演一直是地球物理學家研究的重點和熱點之一。

重磁正演問題分兩大類： 空間域正演和波數(shù)域正演。空間域正演的優(yōu)點是直觀、精度高；缺點是公式推導較難，導出結果繁瑣，對于較復雜的形體，則難以導出正演解析表達式。空間域正演的另一缺點是計算速度慢。波數(shù)域正演的優(yōu)點是公式推導簡單，導出結果簡潔。對于很多空間域無法導出的正演公式，在波數(shù)域中很容易導出。波數(shù)域正演的另一優(yōu)點是計算速度快。波數(shù)域正演的主要缺點是精度低。為了提高波數(shù)域正演計算精度，1988年，Chai等[1]提出了波數(shù)域最佳偏移抽樣法(偏移量為0.22倍波數(shù)域采樣間隔)，將重磁波數(shù)域正演精度提高了幾十倍。2014年，Wu等[2]將柴玉璞[3-4]提出的移樣離散傅里葉變換(SFT)與高斯節(jié)點積分相結合，提出了一種高精度快速位場波數(shù)域正演方法，對重磁勘探技術的發(fā)展做出了很大貢獻，但尚有以下不足。

(1)作者對所提方法的論證是從位函數(shù)譜的性質出發(fā)，未能充分展現(xiàn)高斯FFT算法廣泛的應用領域。

(2)文中缺少將高斯節(jié)點積分引入傅里葉變換數(shù)值計算的數(shù)學演繹過程，不免讓讀者認為文中公式(19)僅源于觀察、公式(20)僅源于猜想。而此種感覺乃數(shù)學論證欠嚴謹所致。

(3)文中未給出偏移量與高斯節(jié)點的換算關系、權系數(shù)與高斯求積系數(shù)之間的換算關系，也未直接給出區(qū)間[0，1]內大于2的高斯抽樣點(即偏移量)和權系數(shù)，無法實現(xiàn)編程。

本文從移樣離散傅里葉變換理論出發(fā)，對高斯FFT算法展開論證，將其應用范圍擴展到任意有界函數(shù)的正、反傅里葉變換。文中給出了將高斯節(jié)點積分引入傅里葉變換數(shù)值計算的嚴謹數(shù)學演繹過程，并在此過程中導出了偏移量與高斯節(jié)點的換算關系以及權系數(shù)與高斯求積系數(shù)之間的換算關系。這樣借助數(shù)學手冊[5]中的高斯型求積節(jié)點和求積系數(shù)數(shù)據(jù)表，即可實現(xiàn)編程。

1 DFT變換的推廣

目前采用的離散傅里葉變換(DFT)表達式為

(1)

(2)

式(2)稱為DFTξη變換，其中0≤ξ,η≤1。這一推廣的正確性顯而易見，把式(2)中的一個等式代入另一個等式，即可證明兩式的互逆性。利用新確立的DFTξ η變換可以表述一個重要定理——傅里葉變換離散化定理。

2 移樣離散傅里葉變換理論和算法

柴玉璞在其發(fā)表在《中國科學》的論文[3]中證明了一個重要定理——傅里葉變換離散化定理。該定理揭示了函數(shù)離散值與其譜離散值之間的關系，并據(jù)此給出了嚴謹?shù)摹⑼黄菩缘母道锶~變換數(shù)值計算理論——移樣離散傅里葉變換理論。

2.1 傅里葉變換離散化定理

設f(x)與F(u)為一傅里葉變換對，且均無無窮型間斷點。依據(jù)下式

(3)

將f(x)和F(u)離散化，并加權折疊成兩個長度為N的復序列(dΔ=1/N)，則兩序列恰好構成一DFTξη變換對

(4a)

或

(4b)

2.2 移樣離散傅里葉變換理論和算法

將式(4a) 中k=0和l=0的兩項置于方程左邊，其余項放在右邊，可得

DFTξ η[f(n+ξ)Δ]-F[(m+η)d]

(5a)

上式即為DFTξ η算法的誤差方程。同理可由式(4b) 導出IDFTξ η算法的誤差方程

IDFTξ η{F[(m+η)d]}-f[(n+ξ)Δ]

(5b)

式(5a)、式(5b)中，左端第一項分別為DFTξ η和IDFTξ η算法表達式，第二項分別為離散真譜和函數(shù)真值表達式，右端為誤差表達式。

實際上，式(5)以數(shù)學語言表述了一個嚴謹且具突破性的傅里葉變換數(shù)值計算理論——移樣離散傅里葉變換。其嚴謹性在于它不僅給出了算法表達式，而且給出了誤差表達式；其突破性在于它給出了更廣義、更普遍的新算法—— SFT算法(式(2))。利用這一新算法，既可由函數(shù)的任意一組等間隔抽樣值計算任意一組等間隔頻點上的譜值，也可以由任意一組等間隔頻點上的譜值計算任意一組函數(shù)等間隔抽樣值。這就為將高斯節(jié)點積分引入傅里葉變換數(shù)值計算創(chuàng)造了條件。因此，將高斯節(jié)點積分引入傅里葉變換數(shù)值計算，是移樣離散傅里葉變換理論的一個重要應用。

3 將高斯節(jié)點積分引入傅里葉變換數(shù)值計算

高斯節(jié)點積分問題有嚴謹?shù)臄?shù)學證明[6]，比較麻煩，也很深奧，涉及拉格朗日插值、多項式正交性、勒讓德函數(shù)等問題。作為應用者，僅將其結論深入淺出地表述如下： 對于區(qū)間[-1，1]上有界函數(shù)f(x)的積分，可用其M個點的函數(shù)值加權求和高精度逼近，其條件是這M個點需是M階勒讓德多項式pM(x)的M個根。高斯節(jié)點積分的數(shù)學表達為

(6)

(7)

高斯節(jié)點積分是針對實函數(shù)的。由于復數(shù)譜的實部和虛部都是實函數(shù)，所以正、反傅里葉變換都可以引入高斯節(jié)點積分。所謂將高斯節(jié)點積分引入傅里葉變換數(shù)值計算，就是將傅里葉積分的N個等間隔子區(qū)間[nΔ,(n+1)Δ]上的積分，轉換為區(qū)間[-1，1]上的高斯積分。眾所周知，對于變量t在區(qū)間[a，b]上的積分可通過變量替換

(8)

轉換為區(qū)間[-1，1]上的積分，即

(9)

利用式(9)將子區(qū)間[nΔ,(n+1)Δ]上的積分轉換為區(qū)間[-1，1]上的高斯節(jié)點積分

(10)

進而可得

(11a)

(11b)

由此可見，傅里葉積分

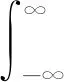
(12a)

可用下式高精度逼近

(12b)

傅里葉積分

(13a)

可用下式高精度逼近

(13b)

由勒讓德多項式的性質可知，高斯節(jié)點具有關于區(qū)間中心的對稱性。式(4b)中的f為實函數(shù)，顯然，利用該式(其左端只保留l=0項，即忽略截斷誤差)可證明，移樣離散傅里葉反變換中，對稱高斯節(jié)點序列的譜具有共軛性。因此，式(13b)可簡化為

(13c)

式(12b)和式(13c)即是一維傅里葉正、反變換數(shù)值計算的實用公式。

柴玉璞在其專著[4]中將一維DFTξ η和IDFTξ η算法誤差方程推廣到二維，其形式與一維完全一致(式(5))。對于二維IDFTξ η算法誤差方程，略去有限效應項，令ξ=0，并將左端k1=k2=0項移到右端，得到

f[(n1+k1N)Δ,(n2+k2N)Δ]

(14)

二維傅里葉變換相當于進行兩次一維傅里葉變換，因此，若將高斯節(jié)點積分引入二維傅里葉變換(方法同一維，只是分別對兩重積分實施)

(15a)

則其積分可用下式高精度逼近

(15b)

式中ξ1,i、ξ2,i分別表示第i個移樣離散傅里葉變換中x軸和y軸上的偏移量。同理，將高斯節(jié)點積分引入二維傅里葉反變換

(16a)

則上式可高精度逼近為

(16b)

式中η1,i、η2,i分別表示第i個移樣離散傅里葉變換中u軸和v軸上的偏移量。由式(14)可判斷，二維傅里葉反變換的第一重變換中，其對稱高斯節(jié)點序列的譜無共軛性，但第二重變換其對稱高斯節(jié)點序列的譜具有共軛性。因此式(16b)可簡化為

(16c)

式(15b)和式(16c)即是二維傅里葉正、反變換數(shù)值計算的實用公式。式中兩重一維移樣離散傅里葉變換的高斯節(jié)點數(shù)理論上可以不同，但一般情況下無此必要，故本文未作區(qū)別。

柴玉璞在其專著[4]中詳細論述了SFT與DFT的關系，并指出SFT仍可借用FFT實現(xiàn)快速計算。其實，只需將DFTξη的定義式(式(2))展開，上述關系和結論便一目了然。

4 位場波數(shù)域正演中的應用

位場是有界函數(shù)，而且其譜呈負指數(shù)規(guī)律快速衰減，所以高斯FFT算法可用于位場反傅里葉變換，且效果特別好。位場反傅里葉變換，即位場波數(shù)域正演，也是重磁勘探的重要課題之一，也特別需要借助這一數(shù)學方法提高計算精度。所以本文選擇位場波數(shù)域正演作為這一數(shù)學方法的應用領域，并沿用Wu等[2]對這一快速、高精度位場波數(shù)域正演方法的命名——高斯傅里葉正演。

設計一個由5個同尺寸的直立方柱體組成的模型。5個直立方柱體的高度均為2km，頂面埋深為1km，頂面面積為10km×10km，剩余密度均取2.0g/cm3。這5個方柱體的平面位置：其中一個的中心與圖1的中心點重合，其余4個的中心分別與圖1的四條邊的中點重合。正演計算面積為64km×64km，網(wǎng)格距為0.5km，網(wǎng)格數(shù)據(jù)點為128×128。圖1是采用空間域方法計算的模型重力異常。圖2為高斯抽樣點數(shù)分別為2、4、6時的高斯傅里葉正演結果及其對應的正演誤差。高斯抽樣點數(shù)為2、4、6時的均方根誤差分別為13.300、0.060、0.001mGal，說明隨著高斯抽樣點數(shù)的增加，誤差急劇減小，當高斯抽樣點增加到4時，精度已可滿足常規(guī)解釋要求。

圖1 方柱體組合模型重力異常圖(空間域正演)

圖2 方柱體組合模型高斯抽樣點數(shù)為2(a)、4(b)、6(c)時的剩余重力異常圖(左)及誤差分布(右)

高斯傅里葉正演的一般規(guī)律是，場源離計算窗中心越遠，其譜的波動頻率越高，則需要更多的高斯抽樣點才能達到期望精度，特別是在源跨越計算窗邊、延伸到計算窗外的情況。當高斯抽樣點為2時，中心方柱體的正演誤差已經(jīng)很小，以至于可以忽略，但周圍四個方柱體的正演誤差仍相當大(圖2a右)；當高斯抽樣點為4時，周圍四個方柱體的正演誤差已微乎其微(圖2b右)；當高斯抽樣點為6時，整個計算區(qū)域內的誤差已經(jīng)降至非常低(約10-3mGal)(圖2c右)。實際上此時的誤差是譜的截斷誤差，它不再隨高斯抽樣點的增加而減小。

理論和實踐都證明，無論場源分布如何，高斯傅里葉正演都能通過增加高斯抽樣點達到預期的精度，且仍能保持位場波數(shù)域正演計算速度快的優(yōu)點。

5 結論

(1)快速傅里葉變換(FFT)解決了傅里葉變換數(shù)值計算的效率問題，但其抽樣點需是一個傅里葉積分被劃分成的數(shù)個子區(qū)間的端點；高斯節(jié)點積分具有很高精度，但其抽樣點須是子區(qū)間內的某些點。移樣離散傅里葉變換(SFT)理論的確立，客觀上為解決這一矛盾創(chuàng)造了條件。因此可以說，在地球物理學家將FFT 和高斯節(jié)點積分相結合、提出位場高斯傅里葉正演算法的創(chuàng)新中，SFT功不可沒。

(2)本文以嚴謹?shù)臄?shù)學演繹，不僅導出了傅里葉積分可以數(shù)個移樣離散傅里葉變換(SFT)的加權求和高精度地逼近的結論，而且導出了偏移量與高斯節(jié)點的換算關系、權系數(shù)與高斯求積系數(shù)之間的換算關系。這為位場高斯傅里葉正演方法的推廣提供了嚴謹?shù)睦碚撝魏途幊虒崿F(xiàn)上的可行性和方便條件。

(3)高斯FFT算法已經(jīng)在位場波數(shù)域正演中得到成功應用。因為高斯節(jié)點積分理論和移樣離散傅里葉變換理論的充分條件，都是任意有界函數(shù)，因此有理由相信，該方法未來有可能在更廣闊的領域獲得更多應用。

感謝中國石油集團東方地球物理公司賈繼軍、鄧玉友和孫喜明三位高級工程師在計算機操作和繪圖方面提供的幫助。