基于模式回溯的#WS(≠)快速定界算法

2020-12-09 09:46:46翟治年盧亞輝潘志剛周武杰

小型微型計算機系統 2020年12期

關鍵詞：資源

翟治年，盧亞輝，俞堅,潘志剛，周武杰，3

1(浙江科技學院信息與電子工程學院，杭州 310023)2(深圳大學計算機與軟件學院，廣東深圳 518060)3(浙江大學信息與電子工程學院，杭州 310027)

1 引言

工作流可滿足性(Workflow Satisfiability,WS)關系到業務安全策略與執行資源分配的協調與否，是安全規劃的一項關鍵驗證[1,2]，并具有執行場景發現問題(Scenarios Finding Problem,SFP)[3]等重要的應用變體.為定量考查WS實例的可滿足性，并擴展可滿足判定的途徑，文獻[4,5]提出了相應的計數問題(Counting Workflow Satisfiability,#WS).它是#CSP(Counting Constraint Satisfaction Problem)[6,7]的特殊形式，具有特定于業務安全的約束配置、可能的流程相關性[2]，步驟數量受限[8]、約束稀疏[9]等特征.在應用上，#WS與安全工作流的資源彈性[10,11](部分資源失效時的WS)問題有密切關系，為其提供了參考指標和驗證手段[4,12].近年來，云制造[13]、眾包[14]等依賴于第3方資源的新型工作流環境得到了蓬勃發展.此類資源具有虛擬、分散、多變等特性，失效和違約風險較高[15]，使業務安全規劃的資源彈性要求變得日益突出，亟待加強#WS等相關問題的研究.

在基本的互斥約束下，#WS已進入#P完全問題類[16]，較NP完全問題更為困難[17].而其全局計數要求又很難適用局部和智能搜索方法.特別地，在第3方資源環境下，候選資源數量大大超過工作流步驟[10,18,19]，給#WS算法造成了新的性能壓力.

現有#WS研究集中在常見的互斥和綁定約束下.其核心問題是僅含互斥約束的#WS(≠)(綁定約束可以多項式時間消去[5])，在求解性能上已取得了一定進展.2015年，文獻[5]將#WS(≠)歸約為邏輯可滿足計數問題(Counting SATisfi ability,#SAT)[20]，借助其高效求解器sharpSAT，取得了一定的實測時間性能.由于歸約所得邏輯變量規模巨大，整體時間復雜度高達O*(2|R||S|)，其中S和R分別為步驟集和資源集.且其所用組件緩存技術極耗內存，空間復雜度也達到同一量級，綜合性能很受局限.2016年，文獻[4]利用基于賦權集容斥原理和快速zeta變換的集合劃分方法，建立了一種#WS(≠)的動態規劃算法，具有O*(2|S||R|)時間復雜度，但其空間復雜度仍為指數級，實際占用增長很快.2016年，文獻[9]通過樹分解技術來利用約束圖的結構信息，應用樹分解回溯計數的方法(Counting Backtracking Tree Decomposition,#BTD)求解#WS(≠)，并對約束驗證范圍進行了簡化，較前述工作更好地控制了空間開銷.而其時間復雜度為O*(|R|W+1)，其中W為約束圖樹分解寬度.在工作流應用常見的低約束密度條件下，W的值通常受限，因而該算法有比較明顯的時間性能優勢.但其對大量資源帶來的性能壓力，缺乏有效的約簡機制.

最近，在WS研究中提出了一種模式回溯法[21,18,22].在互斥等資源獨立性約束條件下，可以有效克服資源集規模造成的解空間膨脹問題，并利用回溯法的優化技術積累.本文將根據模式回溯法的的兩層求解機制，通過精確的模式可行解計數，結合模式資源指派圖的匹配數量定界，提出一種# WS(≠)定界算法.實驗表明，該算法在高資源配比、低約束密度條件下，能夠快速計算#WS(≠)解的上、下界，且其上界比較接近于精確解.

2 預備知識

WS以一組工作流步驟S為變量集、每個s∈S有一個值域Rs?R，其中R是所有資源的集合.對步驟變量的取值，有一組約束C.WS(≠)是C中僅含互斥約束的WS.任何互斥約束c都作用于兩個變量，要求它們取值不同.WS(≠)的目標是求任意一個可行解，即從S到R的一個賦值映射，使其滿足所有約束和(各變量的)值域要求，或指出可行解不存在.而#WS(≠)的目標是統計WS(≠)可行解的數量.通常有解空間搜索或動態規劃兩種求解途徑.

任何部分賦值，即從T?S到R的映射，都有其劃分模式：當且僅當兩個變量賦值相同時，將其歸入同一個塊，相應塊的集合形成賦值變量集T的一個劃分，稱為模式.每個模式都是一組部分賦值的抽象.由此可以得到問題解空間的一個壓縮映像，即模式空間.它是一棵以模式為結點的根樹，描述了對空劃分逐個加入新變量，最終擴展至完全模式的可能路徑.其葉結點對應于所有完全模式.

部分賦值滿足互斥約束c(即其給c的兩個變量分配不同的值)，當且僅當其模式滿足c(即其將c的兩個變量分入不同的塊).若對模式空間進行搜索，發現一個模式違反約束，即可排除以其為模式的所有部分賦值，非常高效.然而，問題解空間是根據值域構造的，搜索時只需要驗證約束.而壓縮為模式空間后，相應于模式結點的部分賦值不一定符合值域要求，從而需要驗證.文獻[18]解決了模式真實性驗證(根據一個模式判定相應的部分賦值有無可能滿足值域要求)的問題，使得可以對模式空間進行回溯搜索，通過可行模式得到WS(≠)的可行解.驗證模式真實性的主要思路是給定任意模式P，為每個塊b∈P計算恰當的資源指派鄰域Nb?Rb=∩s∈bRs，這里Rb稱為塊b的值域.根據P中所有塊的鄰域，可得(資源)指派圖G(P).存在符合WS(≠)值域要求且以P為模式的部分賦值，當且僅當二分圖G(P)存在左(塊側)到右(資源側)完備匹配.按此匹配為完全可行模式各塊中的步驟分配資源，即得WS的一個可行解.特別地，文獻[18]利用子模式相對父模式只有一個差異塊的特點，實現了增量式的真實性判定.只須計算差異塊的鄰域，并計算從差異塊出發的增廣路，即可將父模式指派圖擴展為子模式指派圖，并由前者的匹配修改得到后者的匹配.

3 #WS(≠)的模式回溯定界

現有模式回溯法僅適用于WS(≠).若需統計所有可行解的數量，不僅要相應改變算法結構，而且所得算法將面臨著更嚴重的性能壓力.模式空間不僅實現了整個問題解空間的壓縮，而且將部分賦值歸類為一個個的模式.相對于平面化的搜索空間，這種層次性有利于從宏觀上確定可行解數量的界，在保證一定結果質量的前提下降低計算負擔.本文在文獻[18]剛剛提出的增量模式回溯法基礎上，為#WS(≠)建立了一種模式回溯定界算法(Bounding Algorithm Based on Pattern Backtracking).其問題求解思路可概括為以下幾點：

1.對每個模式P，均使用完全指派圖(對塊b∈P，Nb=Rb)，以防統計時遺漏可行解.WS(≠)求任意一個可行解，在可行解存在性等價的前提下，可以使用更為精簡的指派圖來提高效率.而#WS(≠)不能遺漏任何可行解，只能使用完全指派圖(每個塊的指派鄰域都等于該塊的值域).

2.每個(左到右完備)匹配都可將完全可行模式轉化為一個真實可行解，不同匹配的轉化結果不同.故找到完全可行模式后，對其資源指派圖中的匹配數量計算上、下界，即為此模式所含可行解數量的界.而在驗證模式真實性時，只關心匹配的存在性，求一個匹配即可.

3.用回溯法遍歷模式空間，對每個完全可行模式，計算其所含可行解數量的界，并相加匯總.

4.適當利用約束圖和指派圖的結構信息.通過連通片分解，由前者/后者得到獨立的# WS(≠)/二分圖匹配計數子問題，分別求解，并相乘匯總.

下面給出具體算法.先由上述思路第4點得主控函數.

算法1.#MAIN//計數主控函數

輸入：S、R、 {Rs|s∈S}和C作為全局變量可用，其中C只含互斥約束.

輸出：WS(≠)可行解數量下界LB和上界UB.

1.LB←1;

2.UB←1;

3.分解S和C構成的約束圖，得一連通片集Comps;

4.for(compi∈Comps){

5.Si←V(compi);//V(compi)是compi的頂點集

6.Ci←E(compi);//E(compi)是compi的邊集，每邊對應一條互斥約束

7. 〈LBi,UBi〉←#IPB≠(?,?,?,Si,Ci);

8.LB←LB·LBi;

9.UB←UB·UBi;

10.}

11.return〈LB,UB〉;

其中調用了如下模式回溯計數算法.它體現了前述思路的第1、3兩點.

算法2.#IPB≠(P,&G,M,Si,Ci) //遞歸過程

輸入：已滿足約束和值域要求的模式P；其完全指派圖G=G(P)，&表示傳址；M是G的左到右完備匹配，其大小為|P|；Si和Ci表示一個連通片內的變量集和約束集.

輸出：在Si和Ci導出的WS子問題中，其模式擴展于P的可行解數量下界LBi和上界UBi.

1.LBi←0;

2.UBi←0;

3.if(|∪P|=|Si|){//子問題的完全可行模式

4. 〈LBi,UBi〉←#MATCH(G);//P為滿足C的完全模式，對其指派圖中符合值域的匹配數進行界定

5.}else{

6. 按一定排序規則選擇擴展變量s;//參見文獻[18]

7. 計算用s擴展P形成的滿足C的模式集X(P);

8. for(Pj∈X(P)){//有未搜索的子模式

9. 基于G計算Pj的完全指派圖Gj=G(Pj);//指派圖增量計算，參見文獻[18]

10. 基于M計算Gj的左到右最大匹配Mj;//匹配增量計算，參見文獻[18]

11. if(|Mj|=|Pj|){//Mj完備

12. 〈LBij,UBij〉←#IPB≠(Pj,Gj,Mj,Si,Ci)//遞歸調用;

13.LBi←LBi+LBij;

14.LBi←LBi+LBij;

15. }

16. 恢復G;//利用增量計算時備份的差異信息

17. }//for

18.}//if-else

19.return〈LBi,UBi〉;

相對于用模式回溯求解WS(而不是#WS)，需要注意第16行恢復指派圖是無條件的，并非模式驗證失敗或發生回溯時才進行.算法2可以對完全可行模式進行精確計數.但為了進一步得到真實可行解的數量界，須調用如下的匹配計數定界算法(其中函數LV()和RV()分別取二分圖的左側和右側頂點集).它體現了前述思路的第2、4兩點.

算法3.#MATCH(G)

輸入：從模式(劃分塊的集合)到資源集的二分圖G

輸出：其左到右完備匹配數量的下界lb和上界ub.

1.lb←1;

2.ub←1;

3.對二分圖G進行分解，得到連通片集GComps;

4.for(gcompk∈GComps){

5. if(gcompk是完全二分圖) {

6.p←0;//p表示已考查的左側頂點數

7. for(b∈LV(gcompk)){//對每個左側頂b

8.lb←lb·(|RV(gcompk)|-p);

9.p←p+1;

10. }

11.ub←lb;//可精確計數，上下界重合

12. }else{//非完全

13.lb←1;

14.p←0;//p表示已考查的左側頂點數

15. for(b∈LV(gcompk)){//對每個左側頂b

16.ub←ub·min{|Rb|,|RV(gcompk)|-p};

17.p←p+1;

18. }

19. }//if-else

20.}

在算法3中，對二分圖進行連通片分解后，逐連通片計算匹配數上、下界.若連通二分圖是完全的，不難精確計算其匹配數，由第6-第11行代碼完成.否則，由第13-第18行代碼進行定界.因為可行模式的指派圖必然存在匹配，第13行將下界取1.而上界由第15-第18行代碼計算，其基本思路是將每個左側頂點的值域大小相乘.但是左側頂可匹配的鄰域還會受到一定限制.設b是連通二分圖中第p+1個被檢查的左側頂點.事實上之前每檢查一個左側頂，都是從其可匹配的鄰域中隱含地選擇一個右側頂，形成一條擬匹配邊，得到一個更小規模的匹配子問題.刪除這一對頂點及其所有關聯邊，不影響子問題的計數.因此檢查到第p+1個左側頂時，在相應的子問題中，至多有RV(gcompk)-p個右側頂可匹配.應取其與|Rb|的較小者作為b可匹配的鄰點數上界.

整體上，算法1和現有的模式回溯WS算法一樣，至多對O*(B|S|)(B|S|表示第|S|個貝爾數)個模式結點進行檢查，每個結點處的驗證開銷為多項式級.算法1要對每個完全可行模式進行匹配計數，但由算法3易知，此過程可在多項式時間完成.因此，算法的整體時間復雜度仍為O*(B|S|).算法1沒有特殊的空間需求，和模式回溯WS算法一樣，具有多項式級空間代價.

4 實驗研究

現在對算法1進行實驗研究，并與文獻[5]的sharpSAT歸約(R2sharpSAT)，文獻[4]的#DP和文獻[9]的#BTD簡化(#BTD-S)算法對比.測試環境為主頻3.6GHz/睿頻4.2GHz的Intel Core i3 CPU、8G RAM、CentOS 8系統、GNU C++編譯器(-O3優化)、GMP6.2大整數庫，單個實例執行時限為半小時.

實驗1.4種#WS(≠)算法的性能對比

本實驗將4種算法在不同步驟數量和資源配比下進行綜合性能比較.由于互斥約束通常作用于職責分離的關鍵步驟，故取較低的約束密度.測試實例生成規則是：在[10,20]之間隨機生成20個值，得到相應大小的S；對每個S，隨機取25≤μ≤75，得到μ%|S|大小的R(μ%稱為資源配比)；再從代表分散(D)、低(L)、中(M)、高(D)的4個區間{[1,100],[1,33],[34,66],[67,100]}中隨機選擇授權比例區間AP，對每個s∈S，隨機選取α∈AP，再隨機取α%|R|個不同資源作為Rs；隨機取5≤ω≤15，以概率ω%(稱為約束密度)決定每對步驟之間是否存在互斥約束，得到C，并保持其它參數不變，重復生成5次C，相應得到一組5個同參數實例，測試時對每組的解出實例取平均結果.4種算法測得的解出率(用SP表示)、執行時間、峰值空間如表1所示.

首先將算法1與#BTD-S比較.可以看到隨著實例規模的變化，兩者的空間占用均保持較小的值，且彼此差距不大.因為#BTD-S具有全局動態規劃與局部回溯相結合的算法結構，所以帶有子問題解的緩存，更耗空間一些.算法1在12/20組實例上，平均空間占用不大于對方，略有優勢.在各組實例上，算法1的解出率均不低于對方.這主要源于算法1的執行時間優勢.算法1在與對方解出率相同的15/20組實例(不含第20組實例，兩者均解出2/5，但具體實例不全相同，也不含#BTD-S無數據的第19組實例)上，所需的執行時間也較少，其性能是對方的1.18-368倍不等，平均為54.9倍.在剩余3組兩者均完全解出的實例上，#BTD-S的性能是算法1的10.6-18.2倍，平均14.7倍.整體上，算法1有很明顯的時間性能優勢.

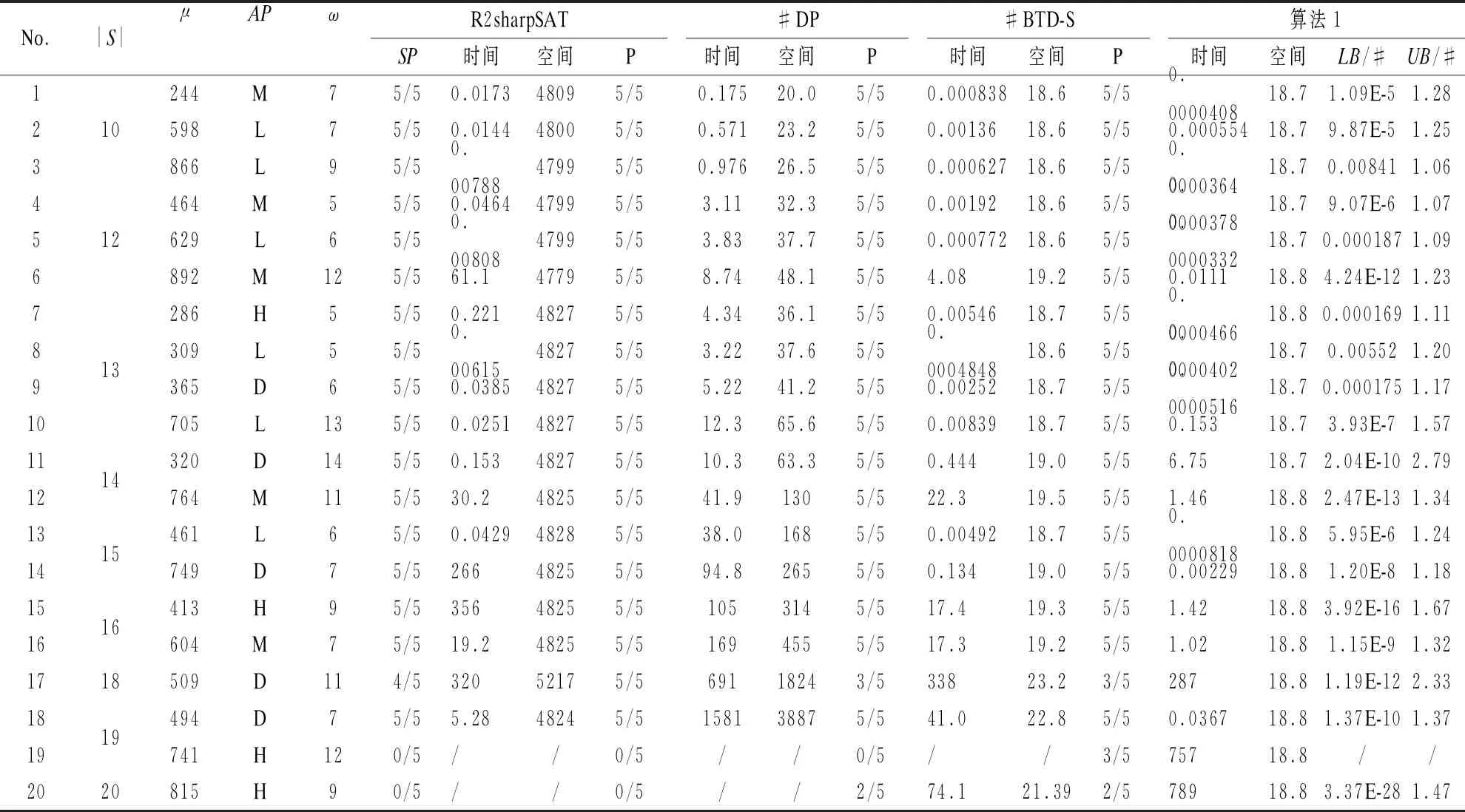
表1 4種#WS(≠)算法的時間(s)和空間(MB)代價Table 1 Cost of time(s)and space(MB)for the 4 #WS(≠)algorithms

將算法1與#DP比較.由于多項式和指數空間復雜度的差異，算法1有明顯的空間性能優勢.由表1可以看到，#DP的空間占用始終高于算法1，且隨著|S|的增大，差距不斷擴大，從1.07倍增長到207倍，平均為22.1倍.#DP的時間復雜度低至2的指數級，較算法1更有優勢.測試表明，在8G內存和半小時限制下，#DP解出了第17組的全部5個實例，而算法1有2個未解出.除此以外，算法1的解出率均不低于對方.在兩者均完全解出的17組實例上，算法1的時間性能均優于對方，比率為1.53-464548倍不等，平均為62019倍.這主要是由于#DP通過系統、規整的計算來控制時間復雜度，且初始開銷很高，對小規模的實例并無優勢.而對于稍大規模的實例，#DP會很快遭遇空間性能的瓶頸.因而其僅在|S|=18(第17組實例)這樣的過渡區域，表現出了一定的優勢.在時間特別是內存資源受限條件下，算法1的整體優勢更為明顯.

將算法1與R2sharpSAT比較.R2sharpSAT始終具有很高的空間占用，達到算法1的258-278倍，平均258倍.R2sharpSAT的空間代價主要由組件緩存導致，由于使用了緩存清理技術，并未隨問題規模明顯增長.在解出率上，R2sharpSAT也在第17組實例上超過了算法1，多解出了1個實例.但其在第19和20組實例上解出率均為0.算法1在與對方解出率相同的17/20組實例上，有15組優勢，時間性能達到對方的18.8-116157倍不等，平均8151倍，有2組劣勢，對方性能是算法1的6.10和44.1倍.算法1仍然有整體上的優勢.

總體上，算法1的綜合性能比較突出.其空間性能僅在個別實例上弱于#BTD-S，時間性能在多數實例上有明顯優勢，但在極少數實例上弱于其它算法.這種優勢首先來源于模式空間對原始解空間的壓縮，其搜索范圍只取決于步驟數量，是與資源數量無關的.同時，在低約束密度下，約束圖結構較為松散，容易形成多個連通片，降低子問題的步驟數量.進而，在葉結點處計算匹配數時，沒有采用指數時間的動態規劃精確計數，而是盡可能分解二分圖，然后通過快速方法定界，使前述兩點優化的效果得以保持.相形之下，#BTD-S雖然也較好控制了內存占用，但其側重于對約束圖的結構進行深入的分解，對于大量資源造成的解空間膨脹問題，缺乏有效的解決機制.而其它兩種算法整體上較#BTD-S更弱，很大程度上是受空間性能制約.當然，其它算法均給出精確的可行解數量，而算法1只能給出其上、下界.表1進一步給出了算法1的界相對其它算法所得精確值的比率(組內各比率求平均，第20組只計算了與#BTD-S共同解出的1個實例).可以看到，其上界質量較好，為精確解的1.06-2.79倍，平均1.41倍.

實驗2.算法1時間性能隨資源配比的變化

如前述，每組實例主要有|S|、資源配比和約束密度3個參數.由實驗1可以看到，算法1的解出率和時間性能隨著|S|的增大，大體上呈現下降的趨勢.工作流應用中，約束密度通常較低，變動不大.而在當前常見的第三方資源環境下，資源配比|R|/|S|向上波動的空間很大.根據實驗1的測試情況，我們選擇|S|=15，取ω=10，在20%、50%、80%三種授權比例下，讓資源配比從4到20，以步長4變化，進一步了解算法1解出率、執行時間和所得界的變化.為消除約束分布偶然性影響，每組參數生成50個實例，結果如表2所示.

表2 算法1執行時間(s)隨資源配比的變化Table 2 Variation of the run-time(s)of algorithm 1corresponding to the ratio of resource

首先，資源配比的增大，使得80%授權的第5組出現了2個未解出實例.進一步觀察可知，隨著資源配比的增加，平均執行時間大體呈增加趨勢.對于偏離趨勢的20%授權第3組實例和50%授權第2組實例，相應的最大執行時間也偏高.異常與這些個別值拉高平均值有關.另外，50%授權的第4組和第5組實例平均值接近，但第5組實例的最大值偏低，其平均值主要源于集體貢獻.對原始數據進行統計，可知第5組較大的值更多，其中位數是第4組的6.2倍，且有37個值不小于第4組的中位數.對于同樣的|S|，模式空間的大小是固定的.上述執行時間隨資源配比增長的趨勢，主要是因為在搜索結點處，為計算模式塊的值域，需要在更大的資源范圍中搜索.當其它條件一定時，更多資源會導致更多滿足約束和值域要求的賦值，故表2中無論LB還是UB都呈現隨資源配比而增長的趨勢.

5 結論與下一步工作