基于響應面方法的噴水推進器進水流道多目標優化

張富毅， 吳欽， 趙曉陽， 劉影， 王國玉

(北京理工大學 機械與車輛學院, 北京 100081)

0 引言

噴水推進器具有推進效率高、抗空泡能力強和附體阻力小等特點，廣泛應用于高速艦艇和兩棲車輛等水面航行體上[1-2]。為了實現水面航行體的機動性、高速性和操縱性，研究作為核心動力來源的噴水推進器顯得尤為重要[3-4]。噴水推進器進水流道是將水流從船底引流到噴水推進泵進口的部件，是噴水推進系統的重要組成部分之一。在噴水推進器工作過程中，有7%～9%的輸入功率在進水流道內損失，而噴水推進系統和船體結構之間的相互作用對推進效率的影響可以達到20%，其中進水流道對泵船相互作用有著重要影響[5]。因此進水流道的流動性能直接影響到噴水推進器整體的推進性能，優化進水流道是提高噴水推進器整體性能的重要途徑之一。

早期對噴水推進器進水流道的研究主要采用模型試驗方法，Brandner等[6]對平口式進水流道展開試驗研究，基于壓力探針觀測了進水流道流動的顯著特征，包括流動分離、空泡產生等。Robert等[7]采用平口式噴水推進裝置研究進水流道的吸水效應，試驗結果表明，針對這種形式的噴水推進器，慣用的設計方法可能會導致對推力的明顯低估。吳民權等[8]采用風洞試驗研究船體- 噴水推進器的相互作用，試驗結果表明進口處的阻力隨著噴速比的增大而減小，并且采用邊界層抽吸方法可以減小進口處大尺度旋渦區，有利于改善泵進口截面的速度分布。

隨著高性能計算機和計算流體力學(CFD)的快速發展，數值模擬方法被廣泛地應用到噴水推進器流場分析評估及性能預報等研究中，并與模型試驗方法結合來證明方法的可靠性。許慧麗等[9]對不同船舶航行姿態下的噴水推進器進行了模型試驗和數值模擬，結果表明計算結果和試驗數據吻合，與直航和斜航相比，倒航狀態下流場更不均勻，壓力更低，更易發生空化和流動分離。靳栓寶等[10]對某軸流式噴水推進器進行改型設計且進行實船試航試驗，結果表明新設計的噴水推進器推進航速超設計航速9.4%，數值預報航速與試航結果誤差為1.5%.

在此基礎上，許多學者針對噴水推進器進水流道影響因素展開進一步研究。魏應三等[11]針對某平口式進水流道，在縱向總長度、寬度、高度給定的條件下，利用CFD技術建立了6種不同傾斜角的進水流道模型，研究傾斜角與流動性能之間的關系，結果表明傾斜角為40°時流動性能最優。丁江明等[12]基于進水流道11個動態關聯的幾何參數，提出了進水流道參數化設計方法，結果表明隨著流道傾斜角的增加，流道背部產生明顯的流動分離。吳娜等[13]通過分析進水流道效率、出流口加權平均角、不均勻系數和唇部駐點位置等參數，建立優選方案進行數值模擬，結果表明減小流道傾斜角可以改善流道出流均勻性，圓弧唇角的流動性能優于拋物線唇角，且唇角形狀應適當尖銳。

本文針對噴水推進器進水流道的內部流場進行數值計算，并采用試驗設計、響應面擬合以及多目標遺傳算法對進水流道設計變量進行優化研究，分析不同進水流道設計變量對流道性能的影響，為噴水推進器進水流道快速優化設計提供一種高效的方法。

1 數值計算方法

1.1 基本控制方程

采用雷諾時均方法求解連續性方程和動量方程：

(1)

(2)

式中：i，j=1，2，3；xi、xj為坐標軸方向；ui、uj為速度分量；ρ為流體密度；p為壓力；μ、μt分別為層流和紊流黏性系數。

1.2 湍流模型

采用剪切應力傳輸(SST)k-ω(k為湍動能，ω為湍流頻率)湍流模型，該模型集合了k-ε(ε為湍動能耗散)模型和k-ω模型的優點：在近壁區域采用k-ω模型，湍流耗散率小，收斂性好；在湍流充分發展區域采用k-ε模型，計算效率高，對復雜流場的適應性更好[14]。湍動能k方程和湍流頻率ω方程分別為

(3)

(4)

(5)

式中：Pk、Pω為湍流生成項；Dk為湍流耗散項；σk和σω2分別為湍動能k和湍流頻率ω的普朗特數；F1、F2為混合函數；S為剪切應變率；Cω、βω和a1為模型常數，取值見文獻[15]。

1.3 數值計算模型

計算采用平口式進水流道，進水口采用矩形+橢圓形，進水流道的軸面結構如圖1所示，由入口過渡段、傾斜直管段、圓弧過渡段和水平直管段組成，各部分幾何參數如表1所示。

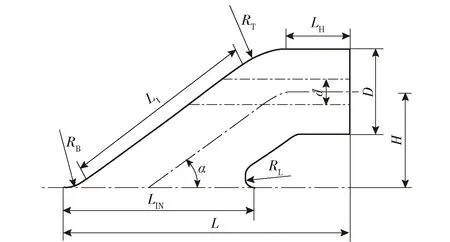
圖1 進水流道軸面結構參數示意圖Fig.1 Structural parameters of axial plane of inlet duct

表1 進水流道幾何參數Tab.1 Geometric parameters of inlet duct

由于進水流道的性能與船體結構以及航行條件密切相關，因此在對進水流道進行數值模擬時應充分考慮船底尾部進水口周圍的流場區域。參考文獻[16]，船底流場控制體的長寬高分別為20D、10D和8D，如圖2所示。流場來流面設置為速度進口邊界條件，出流面和流道出口設置為壓力出口邊界條件，流道壁面、泵軸和船底設置為無滑移壁面，控制域的兩個側面和底面設置為開放邊界條件。

圖2 計算區域及邊界條件Fig.2 Computational domain and boundary conditions

進水流道以及船底控制域均采用非結構化網格，在進水流道以及進水口附近的船底區域進行局部網格加密，在流道和泵軸近壁區采用邊界層網格。整個計算域網格數量為140萬，如圖3所示。動量方程、湍流動能方程和耗散率方程均采用2階迎風格式，收斂精度為10-5.

圖3 網格劃分Fig.3 Mesh generation of water-jet inlet duct

2 噴水推進器進水流道的優化分析

本文采用響應面方法對噴水推進器進水流道進行參數設計及優化。響應面法是一種基于試驗設計理論對指定的設計點集合進行試驗，得到目標函數和約束函數的響應面模型，來預測非試驗點響應值的方法[17-18]。響應面方法優化流程如圖4所示，包括問題設置、試驗設計、響應面擬合和Pareto尋優等過程。

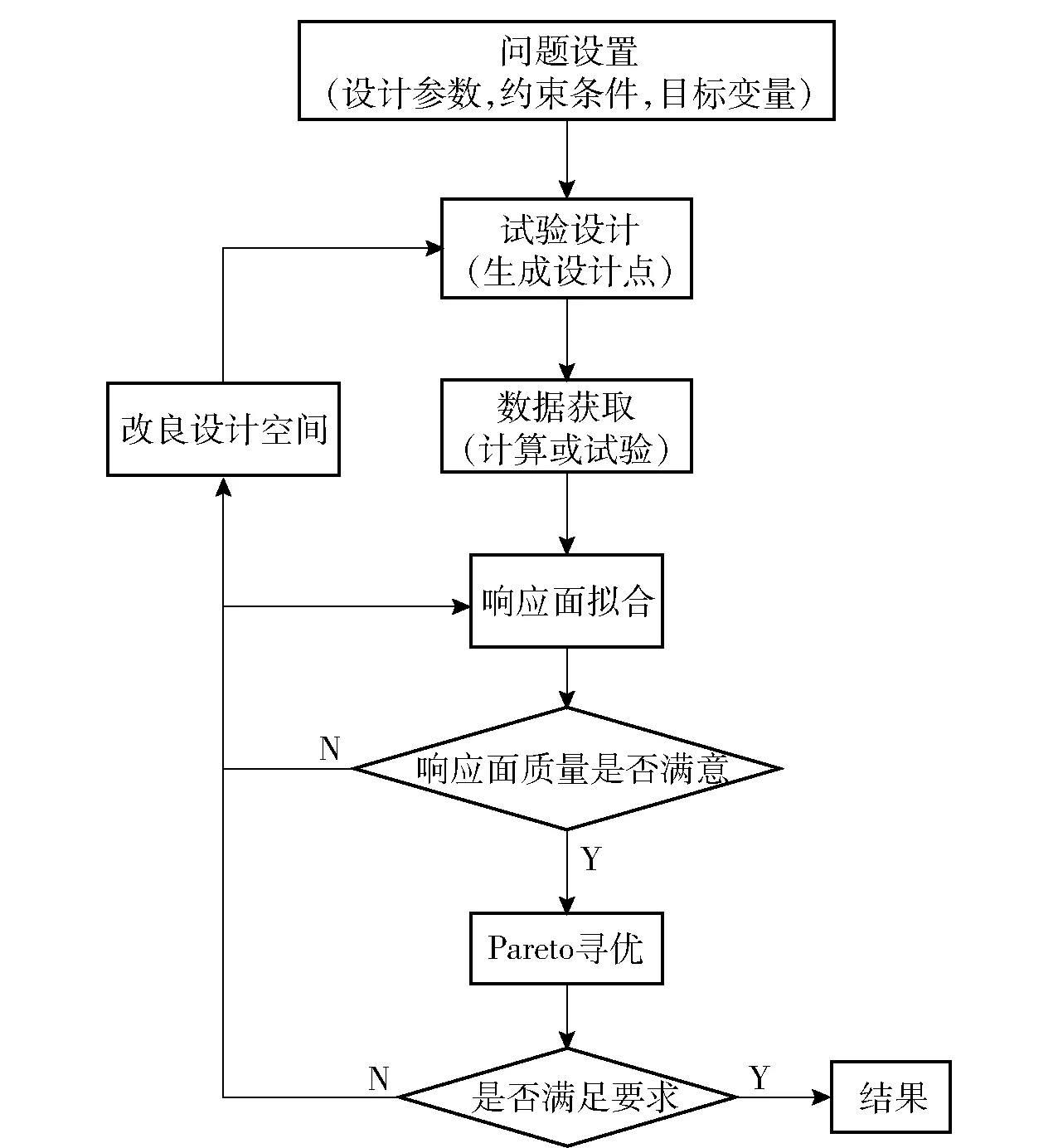
圖4 響應面法優化流程圖Fig.4 Flow chart of response surface optimization

由圖1可知，進水流道出口直徑D由推進泵直徑決定，流道高度H、進水口長度LIN和流道總長度L是由船體整體尺寸確定，結合文獻[10]以及初步理論分析，傾斜角α和過渡段半徑RT對流動性能影響較大，因此本文以傾斜角α和過渡段半徑RT為設計變量，分析二者對流動性能的影響。設計變量取值范圍如表2所示。

表2 設計變量取值范圍Tab.2 Value ranges of design variables

為了定量評估進水流道流動性能，選取流道效率η、出口速度加權平均角θ和出口速度不均勻系數ξ為目標變量[13,19]，分別定義為

(6)

(7)

(8)

對于以上目標變量，流道效率η越高、出口速度加權平均角θ越接近90°、出口速度不均勻系數ξ越小，進水流道流動性能越好。

2.1 試驗設計

試驗設計是在設計變量取值范圍內生成試驗的樣本空間，取樣時應選取具有代表性的設計點，以盡可能少的點最大限度地反映出樣本空間數值特點。本文采用中心復合設計(CCD)方法[20]，如圖5所示，試驗點由以下3部分組成：

1) 一個樣本空間中心點(α，RT)=(40°，450 mm)；

2) 2×2個樣本空間軸向點(α，RT)=(30°，450 mm)、(50°，450 mm)、(40°，300 mm)、(40°，600 mm)；

3) 22個樣本空間析因點(α，RT)=(30°，300 mm)、(30°，600 mm)、(50°，300 mm)、(50°，600 mm)。

圖5 樣本空間示意圖Fig.5 Sample space

為了提高響應面模型的精度，再結合拉丁超立(LHSD)方法隨機生成均勻覆蓋整個樣本空間的26個樣本點，如圖5中的圓點，共計35個樣本點。

2.2 響應面擬合

響應面擬合是以試驗設計中的設計點為基礎，通過一定的函數關系擬合出目標變量與設計變量之間的關系。本文采用2階多項式擬合，具體表達[21]如下：

(9)

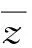
為了對擬合響應面精度進行定量評估，研究基于決定系數R2和均方根差σRMSE來評價響應面模型的預測能力[18]：

(10)

(11)

圖6給出了基于樣本空間設計點的2階多項式響應面擬合優度圖，其中橫坐標是設計點目標變量數值計算結果，縱坐標是設計點目標變量響應面預測值，可以看出，不同目標變量的響應面預測值隨設計點觀測值的變化基本呈現出斜率為1的線性變化，說明響應面擬合精度較高。流道效率η、出口速度加權平均角θ和出口速度不均勻系數ξ的決定系數均大于0.96，均方根差均小于0.1，如表3所示，因此，響應面擬合精度符合要求。

圖6 擬合優度圖Fig.6 Goodness of fit

表3 擬合度評價結果Tab.3 Evaluated results of fit degree

圖7通過比較自變量的偏方差和總方差分別給出了各自變量對目標變量的局部靈敏度和全局靈敏度，即自變量α和RT對目標變量η、θ和ξ的相對重要程度。根據文獻[22]，靈敏度指標定義為

(12)

(13)

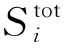
圖7 自變量對目標變量局部、全局靈敏度圖Fig.7 Distribution of local and global sensitivities

對3個目標變量η、θ和ξ的靈敏度分析中發現，傾斜角α對目標變量流道效率η、出口速度加權平均角θ和出口速度不均勻系數ξ的全局靈敏度系數分別為63%、78%和65%，均大于過渡段半徑RT對目標變量的全局靈敏度系數，說明目標變量受傾斜角α的影響較大，即傾斜角α對進水流道的流動性能具有較大影響。

圖8分別給出了流道效率η、出口速度加權平均角θ和出口速度不均勻系數ξ隨傾斜角α和過渡段半徑RT的變化趨勢圖。由圖8(a)圖可以看出，流道效率η隨著流道傾斜角α的增加而降低，而流道效率η隨著過度段半徑RT的變化基本不變。同理，由圖8(b)可以看出，出口速度加權平均角θ隨著傾斜角α的增大有減小的趨勢。由圖8(c)可以看出，當α為30°～40°時，出口速度不均勻系數ξ隨著傾斜角α的增加顯著增大，當α為40°～50°時，出口速度不均勻系數ξ隨著傾斜角α的增大無明顯變化，維持在0.15左右。

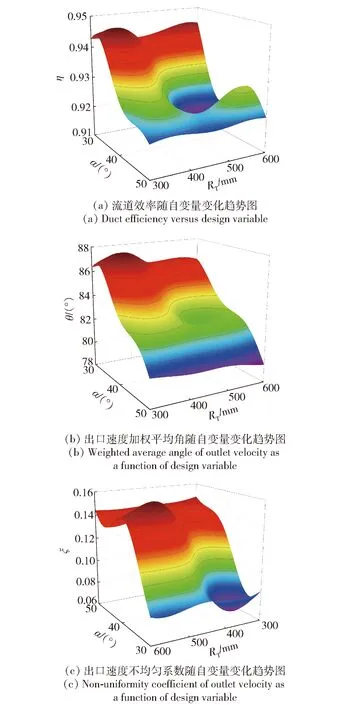
圖8 目標變量隨自變量變化趨勢圖Fig.8 Variation of object variable with design variable

2.3 多目標優化

為了提高流道效率η、出口速度加權平均角θ最接近90°和減小出口速度不均勻系數ξ，建立進水流道的多目標優化數學模型如下：

(14)

式中：Xi為設計變量；Xmin為設計變量下限值；Xmax為設計變量上限值。圖9給出了目標變量相互之間的變化趨勢：如圖9(a)所示，當流道效率η從0.91增加到0.92時，出口速度加權平均角θ由85°減小到83°；同理，由圖9(b)可知，當出口速度加權平均角θ從82°增加到85°時，出口速度不均勻系數ξ由0.04增加到0.06；由圖9(c)可知，當出口速度不均勻系數ξ從0.08減小到0.055時，流道效率η由0.93減小到0.92. 因此，在多目標優化中，無法實現流道效率η、出口速度加權平均角θ和出口速度不均勻系數ξ同時達到最優值，所有可能解構成的解集為Pareto最優解集，它是由那些任一個目標變量的提高都必須以犧牲其他目標變量為代價的解組成的集合[23]。

圖9 目標變量之間相互變化趨勢圖Fig.9 Variations of object variables

為了找出目標變量之間的最佳平衡點，本文采用多目標遺傳算法(MOGA)對(14)式的數學模型進行優化[24]。圖10為MOGA的基本優化流程，采用偏移哈默斯利抽樣(SHS)技術[25選取10N=20個樣本點為初始種群，其中N為自變量個數，計算流道效率η、出口速度加權平均角θ和出口速度不均勻系數ξ，若滿足終止準則則產生終止種群，若不滿足則進行適值分配、遺傳操作和插入父代等過程得到下一代種群，直至滿足終止準則。

圖10 MOGA流程圖Fig.10 Flow chart of MOGA

為了判斷遺傳算法是否收斂，引入最大允許Pareto百分比(MAPP)和收斂穩定性百分比(CSP)。Pareto百分比表示每次迭代樣本數中Pareto點所占的百分比，當Pareto百分比達到MAPP(99%)時，算法收斂；穩定性百分比是基于種群均值和均方差表示全局穩定性的參數，當穩定性百分比小于CSP(0.01%)時，算法收斂，數學表達式為

(15)

(16)

式中：S為收斂穩定性百分比；Yi和Yi-1分別為第i和第i-1代種群平均值；σi和σi-1分別為第i和第i-1代種群均方差；Ymax和Ymin分別為初始種群的最大值和最小值。圖11為Pareto百分比和穩定性百分比隨迭代次數的變化趨勢，可以看出，當迭代36次后，Pareto百分比為100%，大于99%，穩定性百分比為0.03%，趨近0.01%，滿足收斂條件。

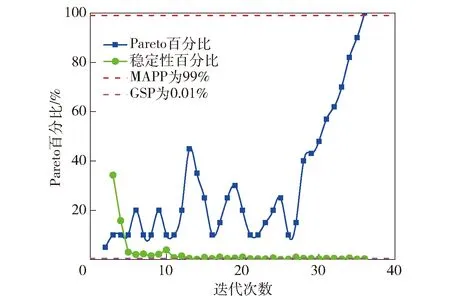
圖11 收斂準則隨迭代次數變化趨勢圖Fig.11 Convergence criterion versus iterations

圖12給出了Pareto解集的分布圖，不同顏色的點表示不同Pareto向前指數(PFI)，PFI越小表示Pareto解越符合要求，可以看出，設計空間內解的分布主要集中在Pareto前沿附近(圖12中紅色區域)，其余區域相對比較稀疏，說明優化過程中設計變量α和RT逐漸向最優目標變量η、θ和ξ靠攏。擇優選出的3個Pareto最優解如表4所示，其中流道效率η均高于0.94，出口速度加權平均角θ均大于87°，出口速度不均勻系數ξ均小于0.067.

圖12 Pareto解集分布圖Fig.12 Distribution of Pareto solution sets

表4 Pareto最優解Tab.4 Pareto optimal solutions

2.4 優化結構分析

為了驗證進水流道優化結果的準確性，對優化點1進行數值計算。表5為進水流道優化前后目標變量數值計算結果的對比，優化后的流道效率η、出口速度加權平均角θ和出口速度不均勻系數ξ都優于原有流道，表明優化后進水流道的流動性能優于原有流道。通過對比分析表4和表5優化點1目標變量的數值，表明基于多目標遺傳算法的目標變量預測值與數值計算的目標變量結果誤差較小，優化結果可靠。

表5 優化前后流動性能參數對比Tab.5 Comparison of flow performance parametersbefore and after optimization

圖13 進水流道三維流線圖Fig.13 3D streamline of inlet duct

圖13為優化前后的進水流道三維流線圖，可以看出：優化前進水流道三維流線存在明顯擾動，尤其是泵軸上方，存在明顯的周向速度；優化后，泵軸上方無明顯擾動，周向速度基本消除，因此提高了出口速度加權平均角θ，進而提高了流道效率η.

圖14對比了優化前后進水流道軸面壓力圖，可以看出：優化前在流道背部和唇部存在明顯的低壓區，流道的抗空化性能較差，泵軸上方壓力分布不均勻，存在較大的壓力梯度；優化后流道背部和唇部的低壓區基本消除，軸面的壓力分布更加均勻，從而提高了流道效率η.

圖14 進水流道軸面壓力分布圖Fig.14 Pressure contour on axial plane of inlet duct

圖15對比了優化前后進水流道出口截面速度分布圖，可以看出:優化前出口截面在泵軸上方存在明顯的低速區，局部區域速度僅1～3 m/s，其余區域速度保持較大值，速度分布不均勻，出口速度不均勻系數ξ較大；優化后出口截面的低速區明顯減小，速度分布更加均勻，出口速度不均勻系數ξ較小。

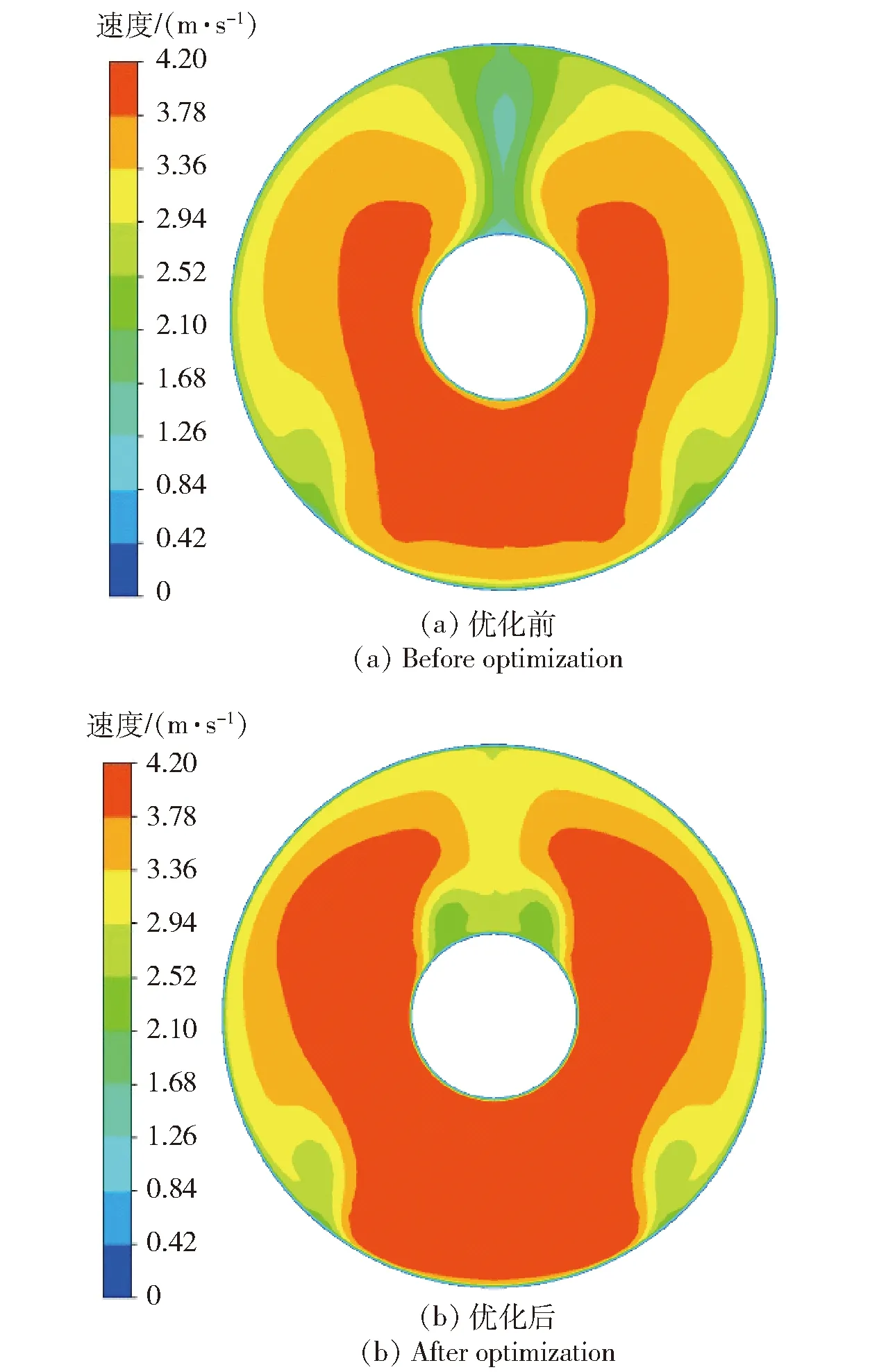
圖15 進水流道出口截面速度分布圖Fig.15 Velocity contour of outlet section of inlet duct

3 結論

本文基于響應面方法對噴水推進器進水流道的內部流場進行優化設計，通過試驗設計、響應面擬合以及多目標遺傳算法對進水流道設計變量進行優化研究，結論如下：

1) 建立的關于流道效率η、出口速度加權平均角θ和出口速度不均勻系數ξ隨傾斜角α和過度段半徑RT變化的響應面模型具有較高的擬合精度，響應面模型預測值與仿真計算值的相對誤差在合理范圍之內。

2) 流道效率η、出口速度加權平均角θ和出口速度不均勻系數ξ受傾斜角α的影響均大于過渡段半徑RT，優化設計過程中需重點對傾斜角α進行優化。流道效率η和出口速度加權平均角θ隨著傾斜角α的增加而減小； 當α為30°～40°時，出口速度不均勻系數ξ隨著傾斜角α的增加顯著增大，當α為40°～50°時，出口速度不均勻系數ξ隨著傾斜角α的增大無明顯變化，維持在0.15左右。

3) 基于多目標遺傳算法的優化方法可以實現進水流道的快速優化，優化后的進水流道較優化前的進水流道相比，流道效率、出口速度加權平均角以及出口速度不均勻系數都有明顯的提高。