讓數學教學生活化

易小軍

數學教學中應重視學生的生活體驗，把數學與學生生活相聯系，把數學問題與生活情境相結合，讓數學生活化。在教學中，可以從現實生活入手，讓學生通過參與數學活動，激發內在的情感體驗和學習興趣。

一、生活情境導入，讓學生主動思考

聯系生活實際，能讓學生在熟悉的生活情境中愉快地探究問題，找到解決問題的規律。教師要善于挖掘數學內容中的生活情境，讓數學貼近生活;要盡量創設生活情境，從中引出數學問題，使學生能積極主動地投入到學習中去。

如在教學《銳角三角函數》（第一課時）時，筆者通過適宜的問題情境引發新的認知沖突;建立知識間的聯系，導入新課。首先出示材料：世界遺產意大利比薩斜塔1350年落成時就已傾斜，其塔頂中心點偏離垂直中心線2.1m。1972年比薩地區發生地震，這座高54.5m的斜塔在大幅度搖擺后仍巍然屹立，但塔頂中心點偏離垂直中心線5.2m，而且還以每年增加1cm的速度繼續傾斜，并且隨時都有倒塌的危險。當地從1990年開始對斜塔進行維修糾偏，2001年竣工，此時塔頂中心點偏離垂直中心線的距離減少了43.8cm。

師：同學們，用什么來描述比薩斜塔的傾斜程度呢？

生1：可用“塔身中心線與垂直中心線所成的角q”來描述比薩斜塔的傾斜程度。

師：根據已測量的數據，你能求角q的度數嗎？在上述問題中可以抽象出一個怎樣的幾何圖形？這實際是一個怎樣的數學問題？？

生2：這個問題可以抽象出一個直角三角形，實際是“已知直角三角形的一條直角邊和斜邊，求這條直角邊所對銳角的度數”的問題。

師：直角三角形中除直角外的5個元素之間的關系，我們已經研究了什么，還可以研究什么？

生3：我們前面研究了直角三角形中角與角之間的關系（兩銳角互余）、三邊之間的關系（勾股定理），還可以研究邊與角之間的關系。

至此，筆者順勢引入課題：直角三角形中的邊角關系，并利用它解決與直角三角形有關的度量問題。

二、借助生活經驗，讓學生在體驗中學

新課程理念指出：數學教學應該從學生的生活經驗和已有的知識背景出發，向他們提供充分的參與數學活動和交流的機會。教師要用創新的教育理念，播撒創新的種子，激活學生的創新思維。

教學《三角形的穩定性》時，筆者出示如下探究問題的情境：

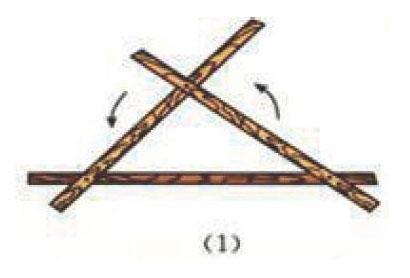
師：如圖（1），將三根木條用釘子釘成一個三角形木架，然后扭動它，它的形狀會改變嗎？

生1：不會。

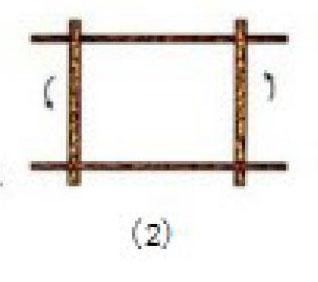
師：如圖（2），將四根木條用釘子釘成一個四邊形木架，然后扭動它，它的形狀會改變嗎？

生2：會。

師：如圖（3），在四邊形的木架上再釘一根木條，將它的一對頂點連起來，然后扭動它，它的形狀會改變嗎？

生3：不會。

學生通過動手扭動木架，獲得了數學經驗：三角形具有穩定性，四邊形不具有穩定性。在學完“三角形的穩定性”這一知識后，筆者又聯想到生活中的情境并提問：“我們的教室里有些桌椅松動了，誰能根據學過的數學知識想一個辦法來解決這個問題？”一名學生回答：“桌椅松動了，就是不穩定，可以用剛學過的三角形的特性——穩定性，解決這個問題。”

在實際運用中，學生的思維更加活躍了，創造意識增強了，解決實際問題的能力也得到提高。

三、問題生活化，讓學生自主探究

在數學課堂教學中，教師有必要給數學問題設置生活背景，把書本上的知識放在生活中來學習，讓數學問題生活化。

例如，教師出示問題：2020年5月，外賣市場競爭激烈，某公司招聘外賣送餐員，每月底薪1000元，另加外賣送單補貼（送一次外賣稱為一單），具體方案如下。

[每月外賣送單數量 補貼（元/單） 不超過500單的部分 6 超過500單但不超過m單的部分

（700≤m≤900） 8 超過m單的部分 10 ]

（1）若某外賣小哥4月份送餐600單，求他這個月的工資總額;

（2）設這個月外賣小哥送餐x單，所得工資為y元，求y與x的函數關系式;

（3）若外賣小哥本月送餐800單，所得工資6400≤y≤6500，求m的取值范圍。

師：假如你是外賣小哥，怎樣解決以上問題？

生1：根據題意和表格中的數據可知，每月送餐在500單之內，每單6元，600單超過500單，但是不超過m單，超過500單的部分按照每單8元，基本工資與這兩部分相加，即可求得外賣小哥4月份送餐600單的工資總額;第（1）問由題意可得，送餐600單的工資總額為1000+500×6+（600-500）×8=1000+3000+800=4800（元）。

師：第（2）問中送餐x單，對應的工資為多少元呢？x確定了嗎？

生2：沒有確定，可根據x的取值范圍分段求出y與x的函數解析式。

師：怎樣分段？

生3：找準臨界值500、m進行分段求。第（2）問由題意可得，當0≤x≤500時，y=1000+6x;當500

師：第（3）問有點難度，同學們先小組合作交流。

生4：根據題意可以列出關于m的不等式，求出m的取值范圍，若800

學生在實際情景中，從數學的視角發現問題、分析問題、構建模型，最終解決了實際問題。

（作者單位：武漢市蔡甸區侏儒山中學）