擴張Schrodinger-Virasoro李代數及其一些子代數研究
余 德 民, 李 笛, 柴 嘉 潞, 羅 德 仁
( 湖南理工學院 數學學院, 湖南 岳陽 414000 )
0 引 言
[Lm,Ln]=(n-m)Ln+m, [Lm,Mn]=nMn+m, [Mm,Mn]=0;
此運算在基向量上線性擴張,并滿足反對稱性和Jacobi不等式,稱g為擴張李代數Schrodinger-Virasoro,文獻[1]研究了擴張李代數Schrodinger-Virasoro的結構,文獻[2]研究了Schrodinger-Virasoro的表示.文獻[3-7]研究了Virasoro李代數及其推廣的Virasoro李代數,文獻[8-10]研究了推廣的Virasoro李代數的結構分類、導子、自同構和最高權模.本文研究這類李代數的子代數、同構.
1 主要結果
定義1若李代數g無非零的交換理想,則稱g為半單李代數.又若李代數g還無非平凡的理想,則稱g為單李代數.
定義2設由Li(?i≥2,i∈Z)張成的子空間為g2.
定理1g2是g的無限維非交換子代數.
證明?i≥2,j≥2,i,j∈Z,可驗證
[Li,Lj]=(j-i)Li+j
(1)
從而,g2是g的子代數,g2也是g的無限維非交換子代數.
定理2g2是g的半單李子代數.
證明由于?i≥2,i∈Z,?j≥2,j∈Z,Li∈g2,Lj∈g2
[Li,Lj]=(j-i)Li+j
g2無二維交換李子代數,反證假設h為g2的二維交換子代數,設x、y為h的基,則x≠0,y≠0,設
x=k2L2+…+kn-1Ln-1+knLn
y=l2L2+…+ln-1Ln-1+lnLn
觀察矩陣:
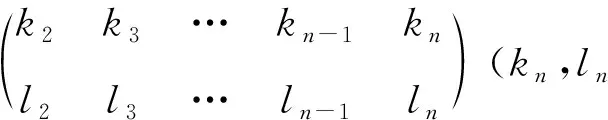
因為h為交換子代數,所以
[x,y]=0
(2)
仔細觀察系數矩陣,式(2)左邊經過具體計算之后可知L2n-1系數為
同理觀察L2n-2的系數
利用行列式有關知識,又kn、ln不全為零,因為
(3)
于是L2n-3的系數
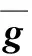
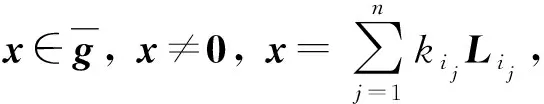
kij≠0,i1 φ1在g2的基向量Li上線性擴張. φ1([Li,Lj])=[φ1(Li),φ1(Lj)]; ?i≥2,j≥2,i,j∈Z 定義3設由Mi(?i∈Z)張成的子空間為g3. 定理4李代數g不是單李代數,也不是半單李代數. 證明先證明g3是g的無限維交換子代數,并且g3是李代數g的交換理想,?i,j∈Z,由于 [Mi,Mj]=0 從而g2是g的無限維交換子代數,?m,n∈Z,由于 從而g2是李代數g的交換理想.從而原命題成立.構造g到g映射如下: φ2:g→g,φ2(Li)=aiLi,φ2(Ni)=aiNi, 定理5φ2是g到g的同構. 定理6g-是g的無限維非交換子代數. 證明?m<0,n<0,m,n∈Z,可驗證 [Lm,Ln]=(n-m)Ln+m, [Lm,Mn]=nMn+m, [Mm,Mn]=0; [Lm,Nn]=nNn+m, [Mm,Nn]=-2Mn+m, 從而g-是g的無限維非交換子代數. 定理7g0-是g的無限維非交換子代數. 證明?m≤0,n≤0,m,n∈Z,可驗證 [Lm,Ln]=(n-m)Ln+m, [Lm,Mn]=nMn+m, [Mm,Mn]=0; [Lm,Nn]=nNn+m, [Mm,Nn]=-2Mn+m, 從而g0-是g的無限維非交換子代數. 顯然,g-?g0-?g. 定理8g-是g0-的無限維非交換子代數,g-是g0-理想. 證明由于g-是g的無限維非交換子代數,當然g-是g0-的無限維非交換子代數.?m>0,n>0,m,n∈Z,可驗證 [Lm,L0]=-mLm, [L0,Mn]=0, [Lm,M0]=0, [Mm,M0]=0, [Lm,N0]=0, [Mm,N0]=-2Mm, 從而g-是g0-理想. 定義6設由Mi,Ni(?i∈Z)張成的子空間為g13.如前所述Mi(?i∈Z)張成的子空間為g3. 定理9g13是g的無限維非交換子代數,g3是g13的理想,g13不是單李代數,也不是半單李代數. 證明?m>0,n>0,m,n∈Z,可驗證 [Mm,Mn]=0, [Mm,Nn]=-2Mn+m,[Nm,Nn]=0 從而g13是g的無限維非交換子代數.顯然g3是g13的交換理想,g13不是單李代數,也不是半單李代數. 定義7設由Li,Mi(?i∈Z)張成的子空間為g14.如前所述Mi(?i∈Z)張成的子空間為g3. 定理10g14是g的無限維非交換子代數,g3是g14的理想,g14不是單李代數,也不是半單李代數. 證明?m,n∈Z,可驗證 [Lm,Ln]=(n-m)Ln+m, [Lm,Mn]=nMn+m, [Mm,Mn]=0 從而g14是g的無限維非交換子代數.顯然g3是g14的交換理想,g14不是單李代數,也不是半單李代數. 本文研究了擴張Schrodinger-Virasoro李代數部分結構問題.可以進一步研究這類李代數的中心和理想,及其全部自同構以及自同構群等結構問題.并可繼續研究擴張Schrodinger-Virasoro李代數的表示.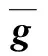
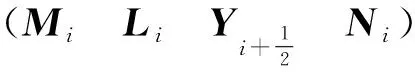
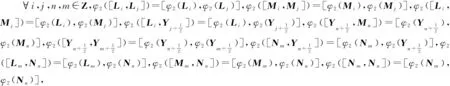
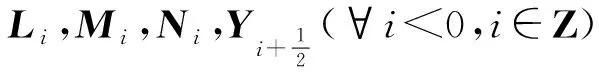
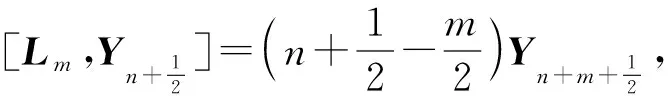
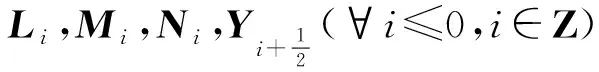
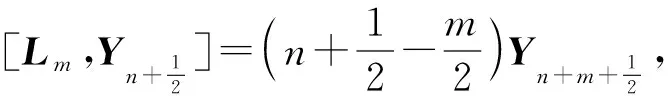
2 結 語

