基于試題分析《概率論與數理統計》的教學方式

（成都信息工程大學統計學院 四川·成都 610103）

0 引言

隨著大數據時代的到來，數據分析已經成為一種新的數學語言。《概率論與數理統計》課程在社會發展中的作用與日俱增，社會對統計分析人才的需求也如饑似渴。該課程是大學理科、工科及經濟管理類學生必修的一門基礎課，是研究和揭示隨機現象統計規律性的一門數學學科。其中概率論是研究隨機現象的概率論分布，數理統計師研究隨機現象的數據收集與處理。《概率論與數理統計》已經發展成為一門與實際聯系密切的數學學科，并應用到工業、經濟、管理等多個領域。

隨著大眾教育的普及，大學生的入學基礎有很大差異且數學課時不斷減少，導致《概率論與數理統計》課程學習效果呈下降趨勢。怎樣培養適應社會需求的綜合性統計人才成為一個值得深思的問題。筆者對多所高校期末試卷進行整理分析，發現了一些明顯的特點，結合這些特點對教學方式進行深度思考，探究怎樣的教學方式對學生數據分析素養的培養有幫助。

1 概率論與數理統計試題特點分析

筆者經過選取四川大學、上海大學、成都信息工程大學等多所高校期末試卷為例，經分析后看出，高校概率論與數理統計期末試題題型考點穩定，考查的知識點覆蓋了概率論與數理統計主要內容：隨機事件及其運算、聯合分布函數與聯合密度函數、統計量及抽樣分布、參數估計、假設檢驗、方差分析。通過對試題研究發現，概率論部分與數理統計部分相對穩定，歸納起來，高校概率論與數理統計試題具有以下特點：

1.1 知識點全面且基礎性較強

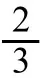
又如數理統計部分試題“設某地區成年女子的身高X～N（ ，2）（單位：m），現隨機抽取成年女子25名，測得身高的平均數為=1.67m，標準差為s=0.038m，求 的置信度為0.95的置信區間。（取小數點后兩位）t0.025(24)=2.0639，）t0.025(25)=2.0595”此題主要是考查三大抽樣分布中t分布的相關內容，解題的要點在于了解題目中的相關已知變量，本題屬于2未知，樣本均值和樣本方差s2已知，根據樣本均值與樣本方差得出總體服從t分布，從而寫出置信區間。此類問題考查學生對三大抽樣分布統計量構造的掌握程度。顯然，這種題目屬于易得分題。

縱觀整個試卷結構，知識點分布，可以看出，大部分高校在試題設計時，注重基礎知識，理論應用較強，大部分考查在于理論知識的轉化運用，并且設題不會出現幾個知識點的融合考題，多只涉及一個知識點，相對來說，基礎性較強。這有利于強化基礎知識，并為能力提升題打下夯實的基礎。

1.2 重概率，輕統計

概率與數理統計課程包含兩大部分的內容，一是概率論部分，二是數理統計部分。其中，概率論部分是理論基礎，數理統計部分則體現了實際應用。數理統計則以概率論為基礎，從試卷選題分析來看，部分高校在學習成果的考查上概率論比重較大，而數理統計部分占比較少，形成重概率，輕統計的教學現狀。部分老師在教學過程中注重理論的理解，所以在概率論部分花費過多課時，調查顯示，在老師實際分配學時時，一般統計數理部分學時僅占到三分之一，因此數理統計部分的學習十分局限，會使學生在正感興趣的時候，課程戛然而止。并且在知識點的講解上時間往往不會很多，缺少理論在實際應用上的講解。

1.3 考核試卷結構分布均勻，題型常規

在選取的幾所高校期末試卷中，四川大學和成都信息工程大學的試題卷主要包括的題型為選擇、填空和解答題。選擇題一般占試卷分值的15%-20%，填空占試卷總分值的20%，填空一般設空較少，分值相對較大，解答題依舊是考查的重點，一般占試卷總分值的60%-70%。試卷整體結構分布均勻，題型常規。在解答題中主要以計算為主，實驗操作圖表解讀較少，在分析的兩套試卷中，成都信息工程大學最后一題涉及方差分析相關圖表的解讀。增加圖表的解讀，更有利于學生對問題的深入了解，更有課程價值。

2 對教學方式的建議

2.1 充分發揮大數據優勢，豐富和調整教學內容

很多概率的相關知識在高中教材中已經涉及到，包括概率運算、古典概型等，因此，在教師在教授概率論內容時可以進行整合調整，將這些內容作為復習內容，從而抽出更多的時間運用于數理統計部分，比如參數估計、假設檢驗、方差分析。不斷提高學生處理數據的能力，增加課程的實用性。當今社會概率論與數理統計方法已廣泛應用于農業、軍事和科學技術領域，它在科學實踐和人類活動中發揮著越來越大的作用。在統計教學中舉例相關統計方法在實際中的運用越來越重要，比如彩票問題、氣象觀測中降雨量分析等等，將這些引入教學研究的內容，可以增加課程的趣味性，讓學生主動學好概率論與數理統計。

2.2 改善傳統教學，融入更多新型教學方式（MOOC、雨課堂）

傳統的教學模式經常是粉筆加黑板，通常情況下是老師在黑板上寫，以老師為中心，學生一邊聽課，一邊記筆記，這樣容易導致學生聽課效率不高，老師單純的板書教學，學生聽課枯燥無味，接收能力不強。教學前期可以通過MOOC等在線學習平臺，通過網絡資源自主預習課程，這樣對于后期老師的教學來說就容易得多，而在教學過程中，通過雨課堂等APP發布考勤活動，保證學生進課堂率，通過課堂提問，發現學生學習問題，通過發布課后作業，檢驗學生課堂聽課效果。多種線上與線下教學方式結合，保證高效課堂。

2.3 注重數學軟件在教學中的引入，增加實操性，培養應用型人才

大數據時代，社會對大學生的需求，不僅要有扎實的理論知識，還要有較強的實際動手能力。培養學生運用MATLAB、SPSS、R、Python等統計分析軟件解決實際問題的能力。增加課程上機課時，將理論運用于實踐中，注重學生對圖表解讀的能力，迅速地發現數據內部的規律，加快對數據的挖掘和分析，這樣不僅能鍛煉學生動手能力，增加實操性，利用現代化統計工具解決實際問題，更有利于培養應用型數學人才。

2.4 優化考核方式

大數據背景下，為促進概率論與數理統計教學質量的提升，應當優化考核方式。目前，《概率論與數理統計》課程學習成果考核方式幾乎都是閉卷考試。題型主要以選擇、填空、判斷、大題等形式出現。通常情況下考核方式為學生平時成績占30%，考試成績占70%，起決定性作用的為考試成績，這就導致學生不注重平時，只突擊考試。建議優化考核方式，將實踐成績加入最終考核成績。實踐成績就是根據學生在實驗課中的表現以及實驗成果所得出的成績。通過多種方式對學生進行考核，利于取得全面、客觀的考核結果，更好了解學生學習情況的同時，利于教師優化教學方法，培養符合當代社會背景對高校人才的需求。

大數據時代背景下，大數據，人工智能，區塊鏈技術層出不窮，對我們來說既是機遇，也是挑戰。信息化技術迅猛發展對人類生活產生了深遠的影響，而高校作為國家一流人才培養基地，對高校老師的科研，教學提出了新的挑戰。概率論與數理統計是大數據的底層理論之一，理工科，經管類學生一門核心課程。在大數據的背景下，掌握概率論與數據統計的知識顯得越發重要了。在這個和未來時代，管理者、決策者、產品經理、產品運營和開發工程師都需要掌握概率論與數理統計的知識。無論是概率論還是數理統計，課程里面的很多方法在數據分析中有著重要的價值，如貝葉斯方法，極大似然估計法，區間估計，假設檢驗，回歸分析，正態分布模型，指數分布模型等。

3 結語

大數據時代下《概率論與數理統計》課程的重要性日益突出，本文從試題角度分析高校教學方式，結合當前教學現象，提出豐富調整教學內容、改善教學模式、增加統計軟件的應用、優化考核方式等來改進現有教學方式。總之，我們應該根據時代的需求，積極優化與改革現有教學方式，培養更多創新性和應用型人才。