下承式系桿鋼拱橋拱腳應力及極限承載力研究

何賓旺， 鄧長根*， 鞏俊松

(1.同濟大學土木工程學院， 上海 200092； 2.中國二十冶集團有限公司， 上海 201999)

下承式系桿拱橋集梁橋和拱橋兩者的優(yōu)點于一體，是梁拱組合體系橋梁的典型代表，造型優(yōu)美，在城市橋梁中應用廣泛。下承式系桿拱橋是復雜超靜定結構，由活載分布構件、力的傳遞構件及主要承重構件組成。其力學原理是將承受壓力的拱肋及承受彎矩、軸力的縱梁組合起來協(xié)同受力，其中吊桿既可作為豎向傳力構件，又可作為縱梁的支承，從而降低縱梁高度，使得結構受力合理，可充分發(fā)揮材料的力學性能，降低總體造價，具有良好的經濟效益[1-3]。系桿拱橋拱腳部位受力復雜，有必要對其進行詳細受力分析[4]。基于深圳空港新城跨截流河3號景觀橋項目，采用有限元方法研究其拱腳在正常使用最不利工況下的應力分布情況及極限承載力，最后給出合理的工程建議，為同類工程提供參考。

1 工程概況

深圳空港新城跨截流河3號景觀橋橋型為下承式系桿鋼拱橋，全長170 m, 主橋采用鋼拱縱橫梁組合體系，下部橋臺采用輕型橋臺，基礎采用樁基礎。橋梁孔跨155 m，全橋橋寬62.0～68.9 m，與河道正交，橋型布置立面圖如圖1所示。在拱支座處各有一巨型拱腳，是端橫梁、中縱梁與拱肋的交叉部位，整個拱腳長15.5 m，寬4.1 m，高10.9 m，重389 t。

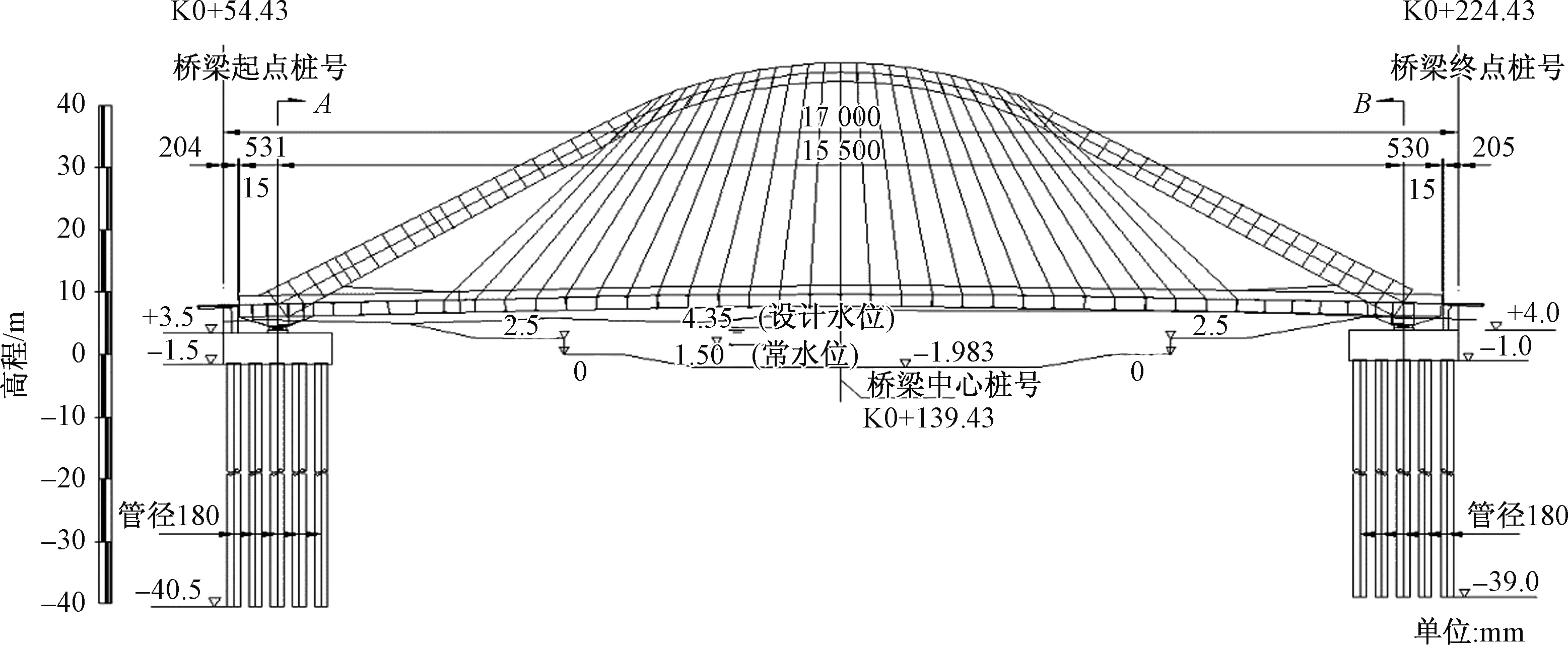
圖1 橋型布置立面圖Fig.1 Elevation of bridge layout map

拱腳采用Q420qD鋼板焊接而成，鋼板厚度為60 mm，加勁肋材料同拱腳，厚度為30 mm，其尺寸及三維模型如圖2～圖4所示。

圖2 拱腳構造立面圖及俯視圖Fig.2 Front and top view map of abutment

圖3 Tekla三維模型示意Fig.3 The 3D model of abutment

圖4 現(xiàn)場施工圖Fig.4 Construction map on site

2 有限元模型

拱腳采用大型通用有限元軟件ANSYS進行有限元數(shù)值分析，分析其正常工作時的應力分布及在相應工況下的極限承載力。拱腳部位鋼材本構采用理想彈塑性模型[5]，彈性模量取2.06×105N/mm2，泊松比取0.3。模型按照實際尺寸建模，為提高建模效率，減小計算代價，選用SHELL181殼單元模擬鋼板[6-7]。考慮計算精度，模型選用較密的網格劃分[8]，單元大體上劃分為四邊形的網格，局部構造復雜部位自動生成三角形網格，拱腳有限元模型如圖5、圖6所示。網格劃分完成后，整個有限元模型共計生成255 670個節(jié)點，262 337個單元。

圖5 拱腳幾何模型Fig.5 Geometric model of abutment

圖6 拱腳有限元模型Fig.6 Finite element model of abutment

邊界條件為固定端約束，在ANSYS中約束模型底板的節(jié)點；在拱肋、縱梁加載面的形心位置建立控制參考點，對該點使用cerig命令使其與整個端部截面自由度一致[9]，以施加軸力、剪力、彎矩等節(jié)點荷載，同時可保證端部截面在整個加載過程中始終保持平面，更符合實際情況。在拱肋端和中縱梁端施加的荷載方向以圖7所示方向為正，其中N1、V1、M1為拱肋荷載，N2、V2、M2為中縱梁荷載，荷載具體數(shù)值如表1所示，均以集中荷載形式加載。

圖7 拱腳受力示意圖Fig.7 Load of abutment

表1 荷載工況Table 1 Load cases

3 有限元分析

3.1 正常工作時的應力分布

通過對拱腳部位在上述4種荷載工況作用下的有限元計算，得到了拱腳應力分布的規(guī)律:在上述4種荷載工況下，拱腳應力大小不同但應力總體分布規(guī)律相似，較大應力存在于腹板底部及拱肋與中縱梁交接部位,最大應力均發(fā)生在內部橫隔板底部位置處,因此僅以最不利荷載工況3進行受力分析。

正常工作最不利工況下拱腳的應力分布情況如圖8所示，拱腳部位的應力平均水平在70 MPa 以下,控制應力420 MPa,應力比為0.16,該設計可保證拱腳在正常使用階段不屈服。在拱腳底部板件連接處會產生應力集中現(xiàn)象[10]，靠近地面約束部位的鋼材易進入塑性狀態(tài)，但拱腳仍可繼續(xù)承載。

圖8 荷載工況3作用下應力Fig.8 Stress distribution of abutment under LC3

3.2 極限荷載系數(shù)和破壞效應

工況3對應的極限承載力作用下拱肋端部加載點的荷載-軸向位移曲線如圖9所示。由此可知，當荷載逐漸增大到拱腳的極限承載力后，拱肋腹板底部部位應力達到材料的屈服強度，由于塑性屈服強度效應使得拱腳底部部位無法繼續(xù)承載，荷載-位移曲線趨于水平，此時對應正荷載工況3下的極限荷載系數(shù)為4.71，即拱腳的極限承載力為工況3作用下的4.71倍。

圖9 極限承載力荷載-位移曲線Fig.9 Load-displacement curve of abutment under ultimate load

拱腳在工況3對應的極限承載力作用下的合位移云圖如圖10所示，拱肋處的合位移最大為63.5 mm,然而在拱腳剛進入塑性時，拱腳的位移僅為15 mm, 可見拱腳具有較大的初始剛度，避免拱腳在正常使用狀態(tài)荷載作用下發(fā)生較大位移。

圖10 極限承載力作用下拱腳合位移Fig.10 Sum-displacement of abutment under ultimate load

拱腳在工況3對應的極限承載力作用下的應力分布云圖如圖11所示，在極限荷載作用下，拱腳腹板下部大范圍進入塑性狀態(tài)，但整體應力分布比較均勻,應力平均水平在46.7～140 MPa范圍之內,具有較大的安全儲備[11]。

圖11 極限承載力作用下應力圖Fig.11 Stress distribution of abutment under ultimate load

4 結論

通過對深圳空港新城跨截流河3號景觀橋拱腳節(jié)點進行有限元計算與分析，可得到以下結論。

(1)拱腳整體應力分析表明，在正常使用狀態(tài)下，拱腳的整體平均水平在70 MPa以下，控制應力420 MPa,應力比為0.16，該設計可保證拱腳在正常使用階段不會大范圍屈服。由于應力集中，約束部位鋼材易進入塑性狀態(tài)。

(2)極限荷載作用下，拱腳腹板底部大范圍進入屈服狀態(tài)，整體呈現(xiàn)拱腳局部塑性屈服破壞效應，屈服后拱腳無法繼續(xù)承載；極限荷載系數(shù)為4.71，受力合理，拱腳具有較大的初始剛度，滿足設計要求。

(3)復雜的構造和受力狀態(tài)使拱腳部位容易出現(xiàn)應力集中現(xiàn)象，為避免應力集中帶來的不利影響，宜在相應部位增加倒角、加腋等措施或者采用鋼板補強的方法增大應力集中部位的剛度，減小應力。

(4)該拱腳在外部箱型結構、內部分割板及加勁肋的協(xié)同作用下具有較大的承載力和剛度，受力合理，鋼材用量較少；在構造上層次感強烈，曲面設計造型優(yōu)美，可以為同類型的下承式系桿鋼拱橋拱腳設計提供參考。