醫療輔助移位機器人剪式升降機構的優化設計與分析

韓以倫， 丁行文， 黃性松， 孫傳禮

(山東科技大學交通學院， 青島 266000)

醫療輔助移位機器人主要應用于醫院、養老院等場合，特別是針對一些行動不便的人群術前或術后的人體移位。醫療輔助移位機器人要與不同型號的床位對接，由于這些床位高低層次不齊，這就要求移位機器人的高度可調以完成對不同高度床位上的人進行移位。在進行移位過程中，為了降低移位對象的恐懼感，所設計的升降機構必須具有高穩定性。移位機器人的發展方向是自動化、智能化，國外的一些科研機構已研發出操作簡單、方便的機電一體化設備。而國內的類似產品結構簡單，功能單一，自動化程度低，因此需要繼續發展完善。

目前，各種場合應用最多的升降機構是剪式升降機構，剪式升降機構是一種作垂直運動的單自由度升降機械，其結構包括底座、支架、起升平臺、驅動執行部件。驅動部件推動支架折疊，從而使起升平臺升降到不同高度。剪式升降機構的特點是結構緊湊穩固、占用空間少、故障率低、運行穩定、安全高效。本文中的醫療輔助移位機器人主要用于身體受過損傷病人的移位，要求實現平穩舉升和下降，結構應盡量簡單。綜合考慮，剪式升降機構是醫療輔助移位機器人的最佳選擇。近年來，不少學者對剪式機構進行了研究。文獻[1]以大型升降機為例，分析剪叉支架的受力情況，利用MATLAB軟件計算剪叉支架的受力大小，并對剪叉支架的強度進行了校核；文獻[2]對剪式機構的動力穩定性運用實驗與建模的方法進行了研究，得出了剪式機構的動力穩定性隨其柔度的增大而減小的結論；文獻[3]建立了二級剪式液壓升降機的機構力學模型，推導出液壓缸推力與載重力和機構尺寸參數之間的關系公式。相對于以上文獻：本文的剪式絲杠升降機的驅動部件是由絲杠驅動，與液壓驅動相比具有無油污，不受環境溫度影響等優點，且絲杠螺母機構的自鎖性能良好，不需要加鎖緊機構；還對剪式升降機構的驅動支架進行了改善，在此基礎上不僅進行了受力分析還進行了運動分析。基于剪式升降機構的簡化模型，依據虛位移原理，建立力學模型，并利用MATLAB軟件進行參數優化。最終采用ADAMS軟件對實體模型進行運動學和動力學仿真分析。

1 醫療輔助移位機器人剪式升降機構的參數設計

以醫療輔助移位機器人的具體工作要求及病床標準為參考，確定了表1所示的醫療輔助移位機器人升降機構具體參數。為滿足醫療輔助移位機器人使用環境中的多種病床高度，制定了最大起升高度和最小起升高度。

表1 醫療輔助移位機器人升降機構參數Table 1 Parameters of lifting mechanism of medical assisted displacement robot

剪式升降機構的驅動源安裝位置參數是影響驅動力矩的重要參數。現對升降機構進行優化設計，確定驅動裝置的最優位置，首先就要建立升降機構的參數化幾何模型，然后進行優化分析。

2 醫療輔助移位機器人剪式升降機構的參數優化

醫療輔助移位機器人剪式升降機構的結構簡圖，如圖1所示。整個升降機構為平衡對象，載重力和驅動力是整個機構的主動力，鉸接約束為理想約束，根據虛位移原理作用于質點系的主動力在任何位移中所做的虛功的和為0[4]，即

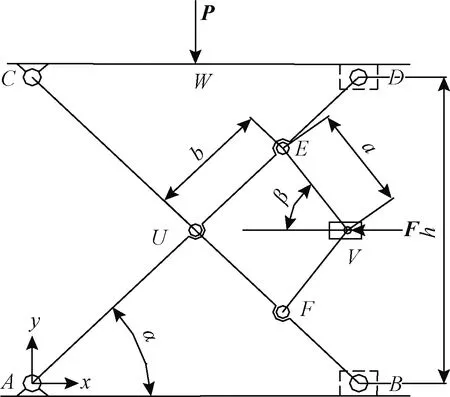
圖1 醫療輔助移位機器人剪式升降機構的結構簡圖Fig.1 Structural schematic diagram of shear lifting mechanism of medical assistance displacement robot

∑(Xiδxi+Yiδyi+Ziδzi)=0

(1)

式(1)中：Xi、Yi、Zi是作用于質點系的主動力Fi在直角坐標系坐標軸上的投影；δxi、δyi、δzi是虛位移δri在直角坐標系坐標軸上的投影。

在圖1中，AB所在的平面是底座，CD所在的平面是上部床位平臺；A、C、E、F、U分別是鉸支點，B、D是滑塊，P是床位和移位對象總重力，W是載重力P的作用點，F是驅動力，V是驅動力作用點;h是上部床位平面到底座平面的距離，h是一個變化值，當上部床位平面位于最低位置是h=hmin，當上部床位處于最高位置是h=hmax。定義底座水平方向為x軸，垂直底座的方向為y軸。由圖1可得：

PδyW+FδxV=0

(2)

式(2)中：δyW表示質點W在y方向的虛位移；δxV表示質點V在x方向的虛位移。

對于W點在坐標系y方向上的坐標由圖1分析可知：

yW=Lsinα

(3)

式(3)中：L為支架兩端銷孔的中心距；α為支架與水平面的夾角。

變分運算后得：

δyW=Lcosαδα

(4)

對于驅動力F的作用點V的坐標由圖1分析可知：

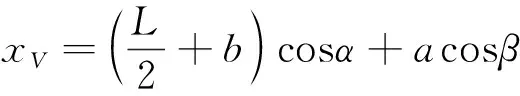
(5)

式(5)中：β為連接桿與水平面的夾角；a為連接桿的長度；b為連接桿端距兩支架交叉孔距離。

由圖1分析可知：

bsinα=asinβ

(6)

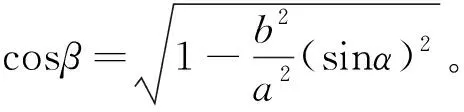
變分運算后得:

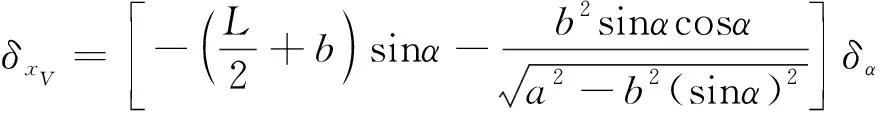
(7)

將式(4)、式(7)代入式(2)，整理可得：

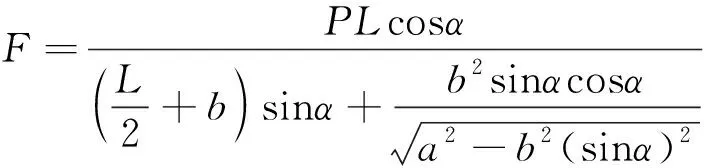
(8)

式(8)為驅動力F與載重力P的關系式。根據式(8)可求得整個升舉過程中任意時刻驅動力。

根據醫療輔助移位機器人升降機構的升降高度選取支架的長度L=800 mm,降機構的最大起升高度和最小起升高度要求選取αmax=55°，αmin=35°。該醫療輔助移位機器人的移位設備(60 kg)、移位對象最大質量(110 kg)、床板質量(10 kg)，三者之和乘以一定的過載系數為升降機構承載的總重力P，最終確定P=2 500 N。

由文獻[5-6]可知，隨著升降機構上升，所需的驅動力減少，故機構處于最低位置αmin=35°時，螺母機構提供的驅動力F最大。當載荷給定時，最大驅動力Fmax決定其工作性能[7]，將L=800 mm,P=2 500 N，α=35°代入式(6)，整理得：

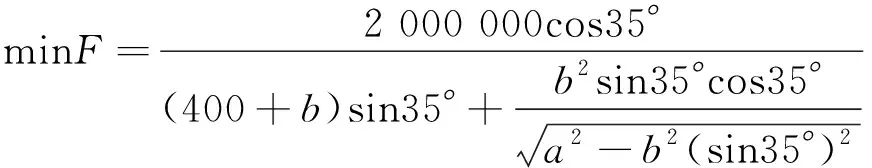
(9)

將式(9)確定為優化目標函數，將a和b這兩個變量作為優化問題的變量。利用MATLAB中的fmincon函數進行參數優化，確定約束條件為180≤a≤400，180≤b≤300，-a+sin55°b≤-20。

設定自變量的初始值a=150,b=150,經多次迭代，目標函數趨于收斂，最終確定其最優化參數為a=265 mm，b=300 mm。將優化前后的驅動力F及連接桿起升角度β的變化趨勢分別繪制成圖，對比曲線如圖2、圖3所示。

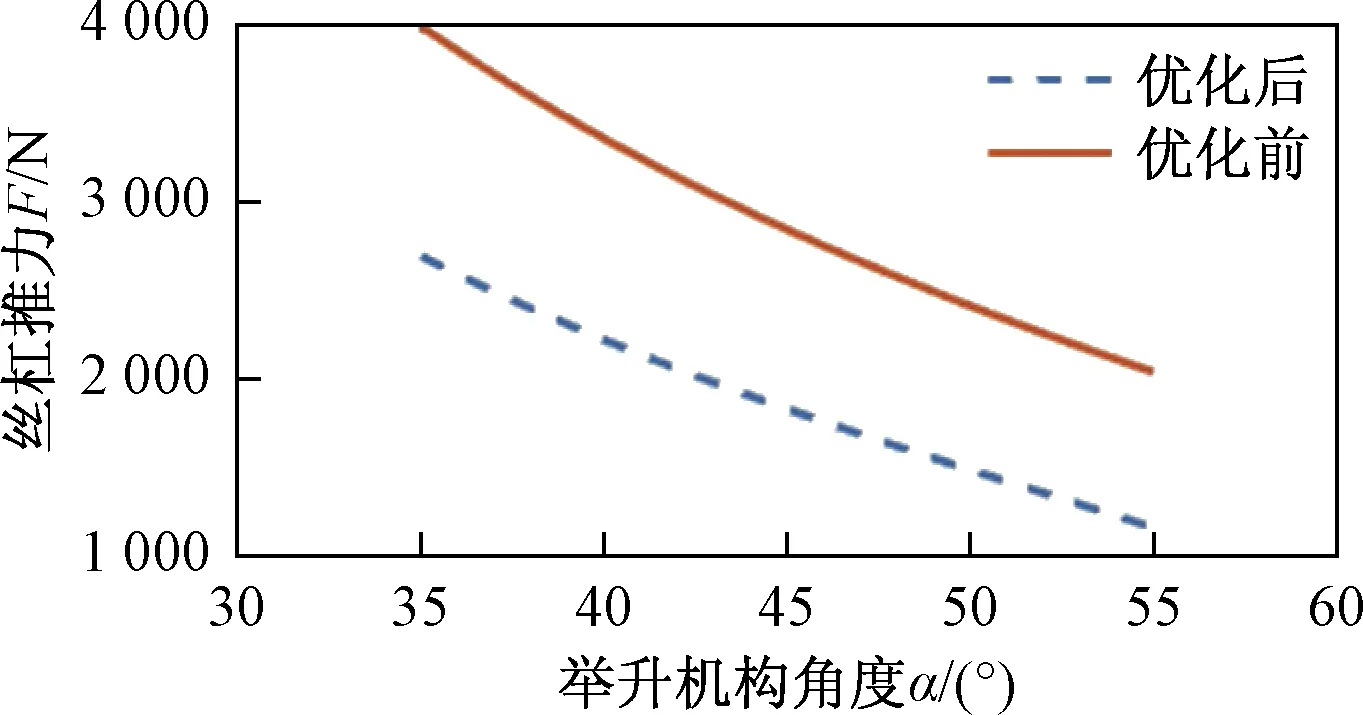
圖2 優化前后驅動力F的趨勢對比Fig.2 The trend comparison of driving force F before and after optimization

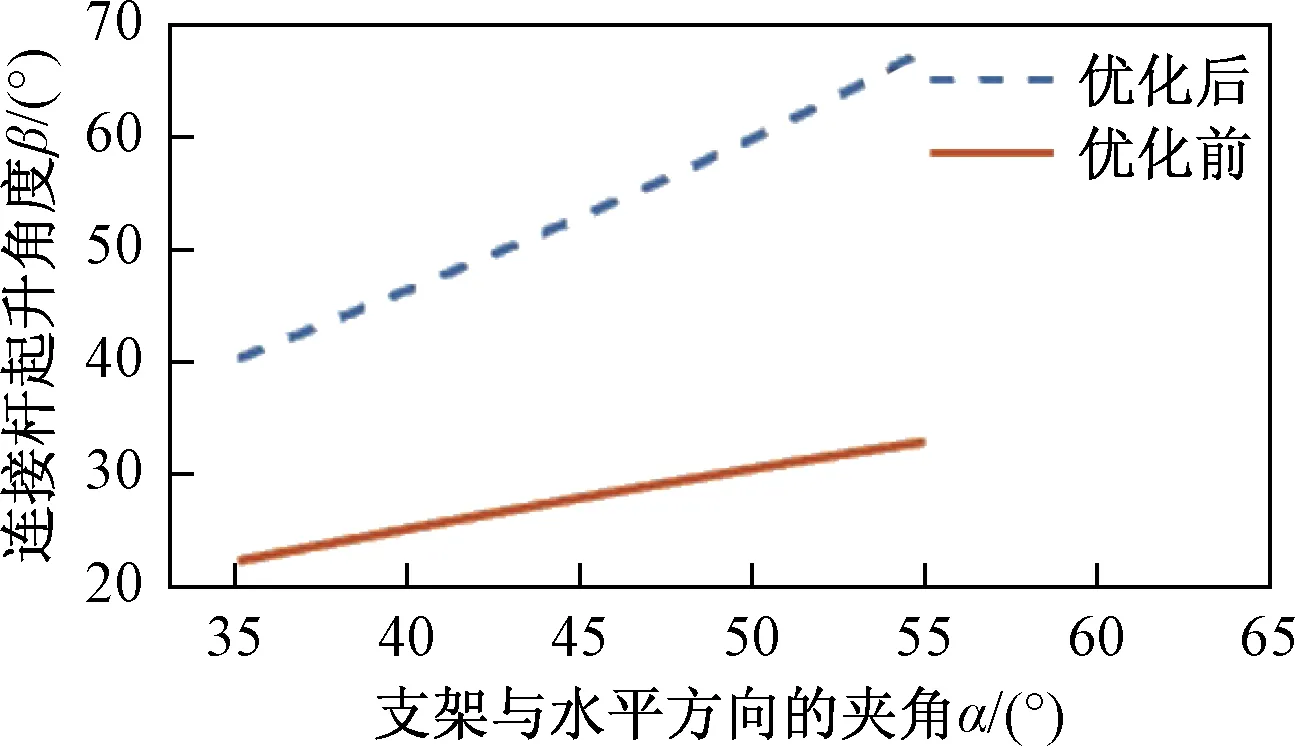
圖3 優化前后連接桿起升角度的趨勢對比Fig.3 The comparison of the trend of lifting angle of the connecting rod before and after optimization

綜合圖2、圖3分析可知，優化后的最大驅動力F1max=2 679 N，驅動力F1min=1 147 N，最小驅動力較最大驅動力下降了57%，驅動力變化曲線較優化前平穩了些，提高了該升降機構的穩定性。此外優化前最大驅動力F2max=4 080 N,優化后最大驅動力F1max=2 679 N，升降機構最大驅動力下降了34%。

3 剪式升降機構的運動學和動力學仿真

3.1 升降機構虛擬樣機模型的建立

由于ADAMS軟件的建模能力差[8]，尤其是對一些復雜的模型更顯遜色，所以選擇PROE三維設計軟件建立了醫療輔助移位機器人剪式升降機構模型，將其保存成Parasolid格式，然后導入到ADAMS/View工作環境中，設置主參考系OXYZ,將單位設置成MMKS單位組。

導入模型后，需要對模型添加約束，即一個構件限制另一個構件的運動，這些約束可以將各構件按照確定的順序完成既定的運動，從而組成完整的系統。由于剪式升降機構兩邊對稱，X方向不受力，故升降機構兩邊對稱的各個構件之間的約束關系相同，剪式升降機構虛擬樣機左側的各構件之間的約束關系[9]，如表2所示。

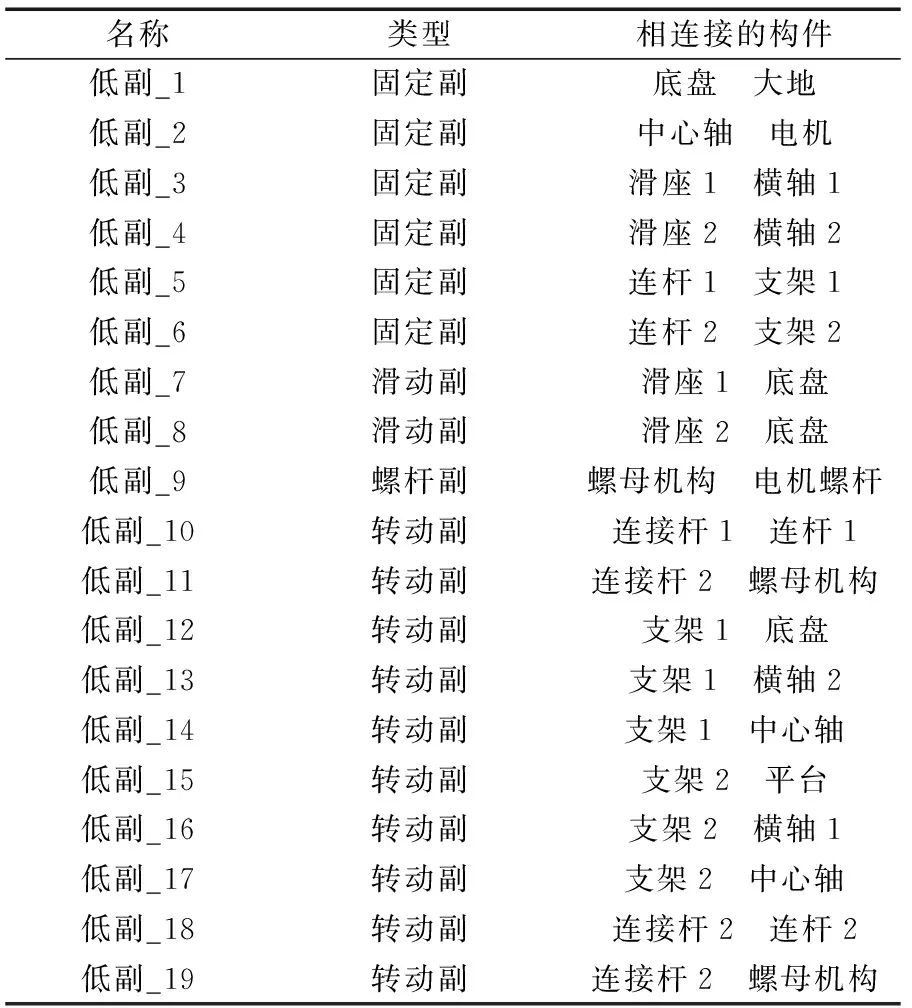
表2 虛擬樣機運動約束副的設置Table 2 Setting of motion pair constraints for virtual prototyping

3.2 運動學仿真結果分析

醫療輔助移位機器人剪式升降機構的仿真模型如圖4所示。對模型施加載荷和驅動[10]，根據升降機構的實際運行情況，在平臺質心處施加方向為Z軸負方向，即垂直地面的作用力，大小為2 500 N，為實現絲杠螺母機構的滑移運動，需要在螺母機構的螺桿副施加驅動，驅動函數為STEP(time，0，0，12，6)+STEP(time，30，0，40，-6)，設置運動時間為 20 s，步數為500，便于進行運動學和動力學仿真。

圖4 剪式升降機構ADAMS建模Fig.4 ADAMS modeling of lifting mechanism

經過上述對模型的設置，對升降機構進行仿真計算，仿真結束后，在后處理器ADAMS/PostProcessor環境下繪制測量曲線，得到升降機構上升階段的運動規律如圖5所示，下降階段，反之。

圖5所示為平臺在Z方向的位移、速度、加速度曲線。由位移曲線可知，平臺在最低位置開始升起時，在Z方向的位移隨時間呈非線性增加趨勢，剛開始起升時，其Z方向的最小位移約為338 mm，隨著絲桿螺母機構的緩慢移動，平臺逐漸開始上升，在上升到極限位置時，其最大位移約為538 mm,其在Z方向的升降行程為200 mm，與醫療輔助移位機器人剪式升降機構所設計的基本性能參數相符。由速度曲線可知，平臺在上升的整個運動過程中，初始階段平臺的速度為0，隨著平臺的上升，平臺速度先呈非線性增大，在12 s時，平臺的速度達到最大約為8.75 mm/s，在12～30 s,平臺速度變化相當緩慢，隨后速度呈非線性減少，在終止階段速度為0。由加速度曲線可知，平臺在上升的整個過程中，0～12 s時，加速度的大小先增大后減小；在12～30 s 時趨于平緩，加速度基本不變；在30～40 s，其加速度絕對值先增大后減小。同時由圖5可以明顯看出，其加速度絕對值最大為0.001 2 m/s2,遠遠小于0.315 m/s2，說明躺在醫療輔助移位機器人上的病人，在升降過程并無不適感，滿足設計要求。

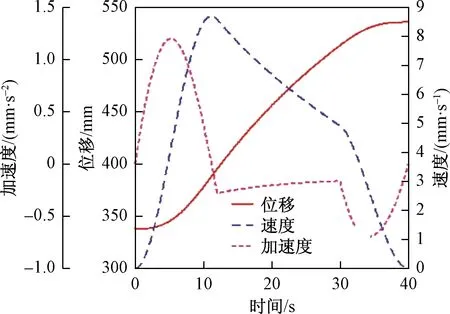
圖5 平臺的位移、速度、加速度曲線Fig.5 Displacement velocity, acceleration curve of platform

圖6所示為支架與水平方向的夾角α和連接桿與水平方向的夾角β變化曲線，夾角α和夾角β隨著時間的增加呈非線性增加，初始位置時，夾角α和夾角β最小，分別約為35°、40°，隨著平臺的不斷上升，夾角不斷增大，當上升到極限位置時，夾角α和夾角β達到最大，分別約為55°，68°，此仿真曲線與理論計算結果相符，驗證了理論計算的正確性。

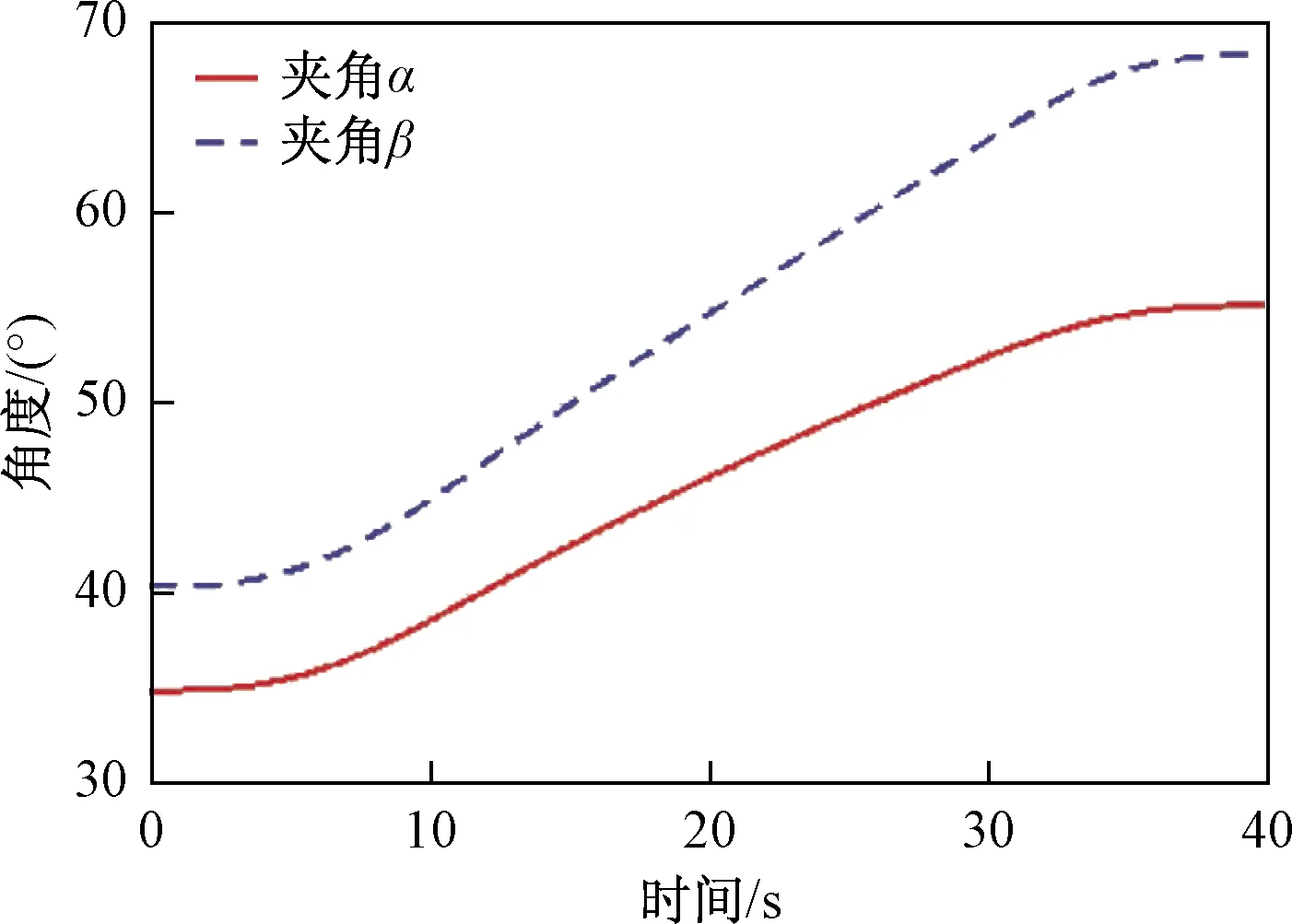
圖6 支架、連接桿與水平方向的夾角變化曲線Fig.6 The angle change curve between bracket and horizontal direction

通過對醫療輔助移位機器人剪式升降機構運動學仿真分析可以看出，在0～40 s的整個仿真過程中非常平穩，符合機構的運動規律，在啟動和停止階段升降機構的運動曲線沒有發生突變，即該升降機構沒有發生沖擊和震蕩，整個運動過程中的加速度值也遠遠小于0.315 m/s2,病者并無不適感。

3.3 動力學仿真結果分析

為了驗證醫療輔助移位機器人剪式升降機構運行的有效性和可靠性，以升降過程中構件之間交接點處的作用力為例進行分析，通過ADAMS中的后處理模塊可以得到仿真曲線，具體分析結果如下。

3.3.1 支架與平臺及中心軸鉸接點處的受力分析

由于醫療輔助移位機器人剪式升降機是兩邊對稱的，故研究支架鉸接點處的受力分析，只需分析升降機構的一側受力，即研究鉸接點Joint_15和鉸接點Joint_17處的受力分析。

在升降機構上升階段，支架2與平臺鉸接點處隨時間變化產生的受力曲線如圖7所示。支架2與中心軸鉸接點處隨時間變化產生的受力曲線如圖8所示。支架2鉸接點處Joint_15及Joint_17的受力隨時間的增大呈非線性減小，平臺在上升的初始階段時，鉸接點處Joint_15及Joint_17的作用力達到最大, 隨平臺的上升，支撐體重心發生變化，其鉸接點處Joint_15及Joint_17的作用力也隨之減少，在終止階段達到最小，每個鉸接點處，Y方向的受力變化范圍0～1 300 N,最大受力不超過2 150 N，Z方向的受力變化范圍0～1 100 N，最大受力不超過 1 200 N。整個上升過程，鉸接點處力的變化相當緩慢，沒有出現突變情況，使得鉸接點處的安全系數較高。

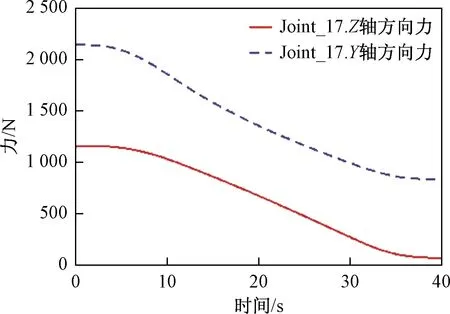
圖7 支架2與平臺鉸接點處的受力曲線Fig.7 The force curve at hinge point between bracket 2 and platform

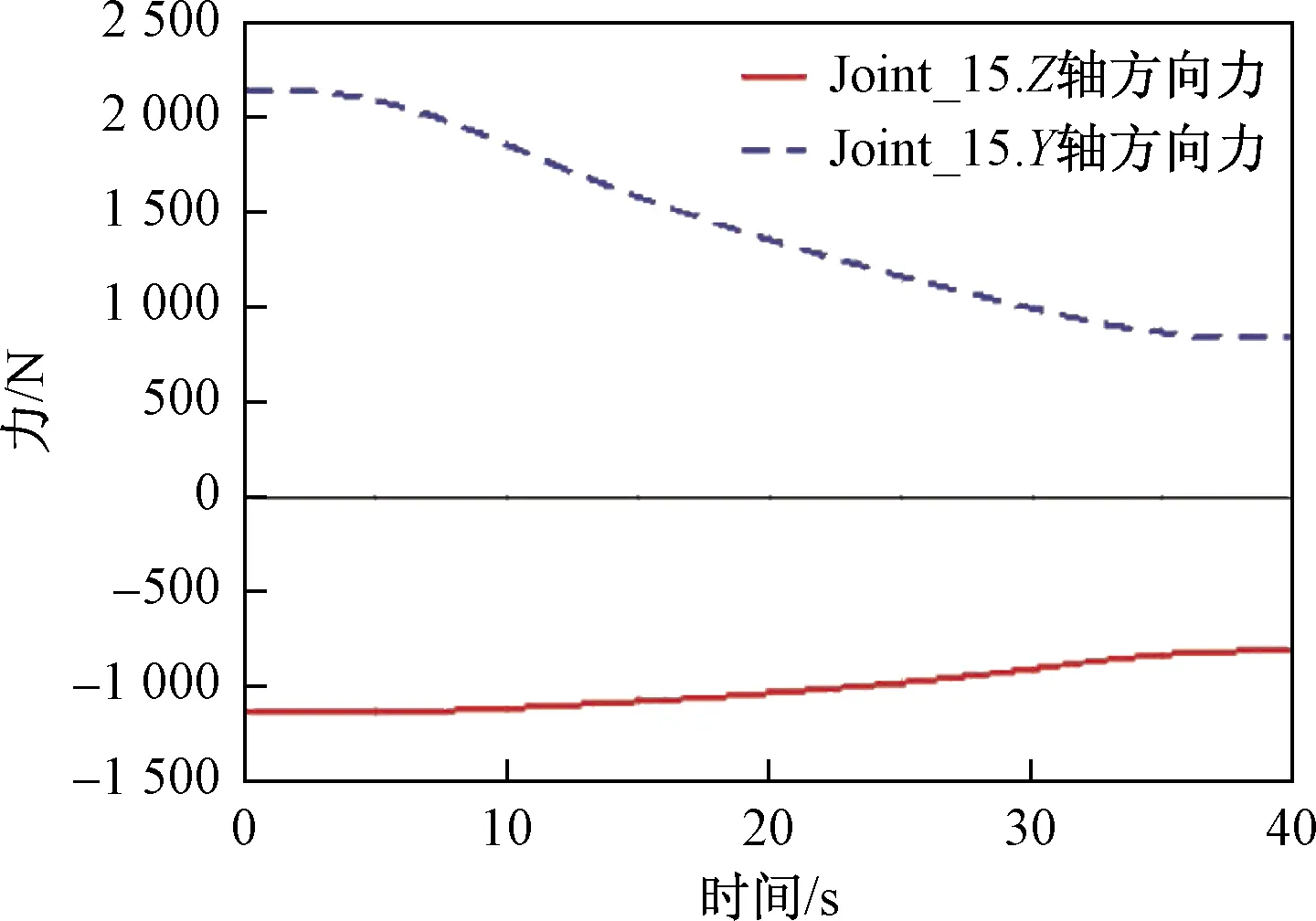
圖8 支架2與中心軸鉸接點處的受力曲線Fig.8 The force curve at hinge point of support 2 and center axis

3.3.2 連接桿與連桿鉸接點處的受力分析

同上所述，只需研究升降機構一側的連接桿與連桿的受力分析，即Joint_18處的受力分析。

在升降機構上升階段，連接桿2與連桿2鉸接點處隨時間變化產生的受力曲線如圖9所示。連接桿2與連桿2鉸接點處的受力隨時間的增大呈非線性變化，在平臺上升的初始階段，鉸接點Joint_18處Y方向的受力達到最大，約為2 146 N，Z方向的受力達到最小，約為1 831 N,隨著平臺的上升，重心轉移，其鉸接點處Y方向的作用力隨之減少，而Z方向的作用力隨之增大，在終止階段，Y方向的作用力達到最小，約為842 N，Z方向的作用力達到最大，約為2 121 N，整個過程沒有出現力的突變情況，使得鉸接點處的安全系數較高。

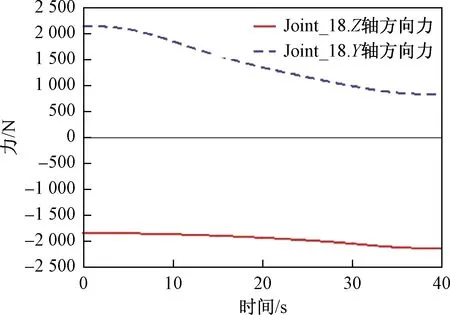
圖9 連接桿2與連桿2鉸接點處的受力曲線Fig.9 The force curve of connecting rod 2 and connecting rod 2 at the hinge point

3.3.3 電機驅動力及驅動功耗分析

圖10所示為電機驅動力及驅動功耗曲線，由圖10驅動力曲線可以看出驅動力的大小隨時間增大呈非線性減少，在初始階段，電機需要驅動螺母機構沿電機絲杠水平移動，從而推動連接桿，此時平臺處于最低位置，支架與水平方向的夾角最小，水平方向的分力較大，因此所需的驅動力達到最大，約為2 679 N。在平臺逐漸上升的過程中，支架與水平方向的夾角逐漸變大，水平方向的分力逐漸變小，因此所需的驅動力緩慢減少，在運行到37 s時，驅動力基本保持在1 147 N左右，下降階段反之，與前文計算的理論數據相符。整個運行過程中，既沒有產生突變，也沒有出現震蕩情況，說明整個系統在運行過程中是非常平穩可靠的。

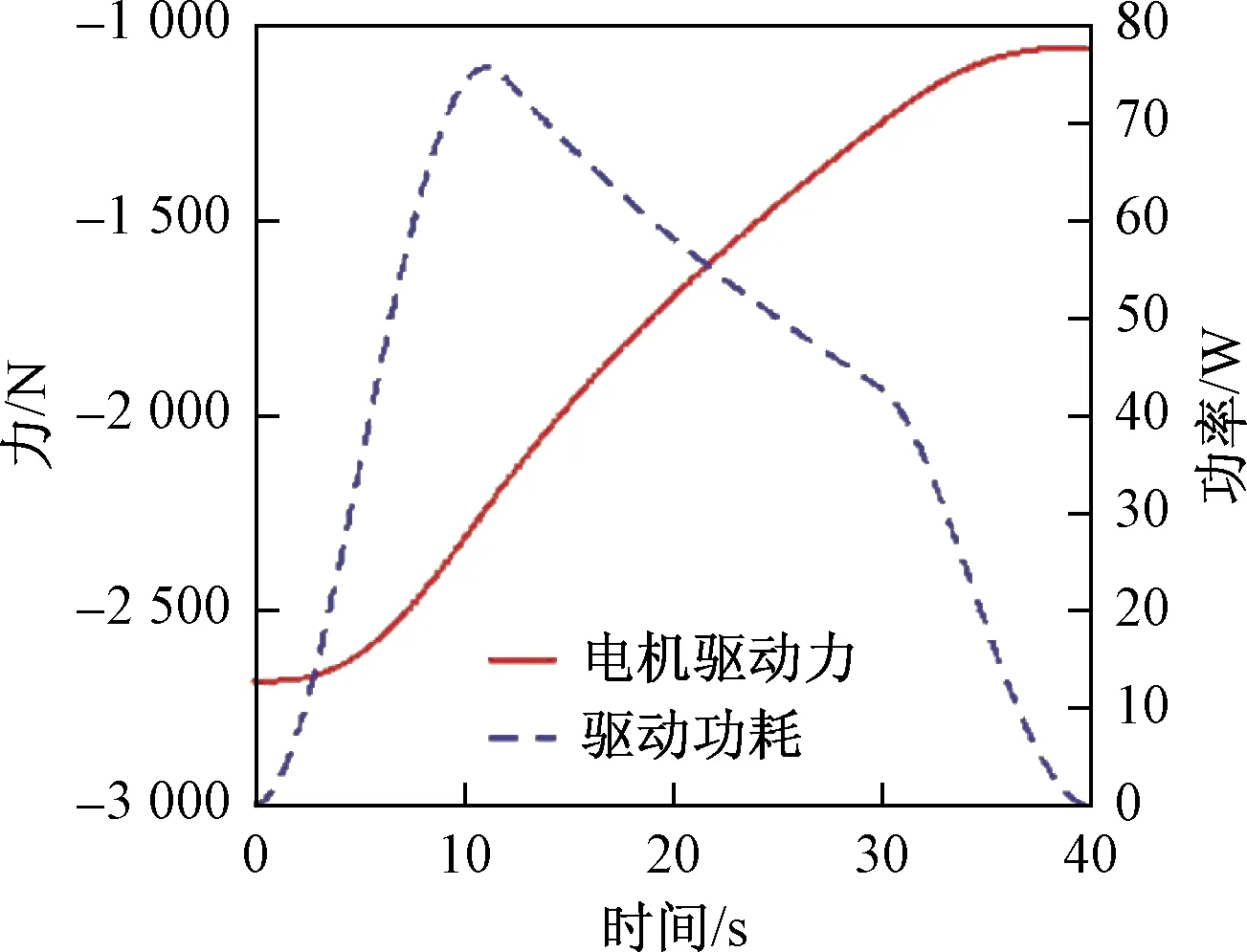
圖10 電機驅動力及驅動功耗曲線Fig.10 The curve of motor driving force and power consumption

驅動功耗曲線對應著工作時的能耗，影響力學性能。由圖10驅動功耗曲線可以看出，電機在整個上升過程中功耗隨時間的變化先上升后下降，在 0～12 s，功耗變化速度非常快；在12 s時功耗達到最大值，約為78 W；在12～31 s時，隨著平臺的不斷上升，電機的功耗開始降低，在31 s時電機功耗為 40 W，在31～40 s電機的功耗相比在12～31 s時下降速度變化快，在最后2 s時，功耗緩慢減少至0，此時平臺上升到最高位置。

綜上所述，醫療輔助移位機器人剪式升降機構模型能夠順利完成運動學和動力學仿真，并且與實際驗證結果相符，為下一步實現自動化的研究奠定了基礎。

4 結論

(1)以醫療輔助移位機器人的具體工作要求及病床標準為參考，確定了醫療輔助移位機器人升降機構具體參數。根據虛位移原理對升降機構的模型進行力學分析，利用MATLAB中的fmincon函數對位置參數進行優化，最終得到的絲杠推力變化曲線較優化前平穩了些，提高了該升降機構的穩定性，同時也為升降機構的運動學和動力學仿真提供了理論數據基礎。

(2)利用三維建模軟件Proe建立了醫療輔助移位機器人剪式升降機構的實體模型，采用ADAMS虛擬樣機技術對該機構進行運動學和動力學仿真，在仿真過程中能夠看到剪式升降機構在運行過程中的位移，速度及受力情況，為該升降機構的實際運動控制提供了重要參考。