基于遺傳算法的柔性車(chē)間調(diào)度優(yōu)化

郭 慶， 張明路， 孫立新， 劉 軒

(河北工業(yè)大學(xué)機(jī)械工程學(xué)院， 天津 300131)

車(chē)間生產(chǎn)調(diào)度作為關(guān)鍵技術(shù)和核心內(nèi)容在離散柔性制造生產(chǎn)計(jì)劃中起主要作用[1]，因?yàn)槊總€(gè)企業(yè)車(chē)間的生產(chǎn)資源是有限的，并且工件的加工也會(huì)受到設(shè)備工藝的限制，如何合理安排每個(gè)工件的每個(gè)生產(chǎn)步驟在哪臺(tái)設(shè)備上加工，以確保所選定的目標(biāo)的最佳性能，這就是調(diào)度的目的。該問(wèn)題的特征在于顯著的離散性、復(fù)雜性、多重約束和不確定性。傳統(tǒng)作業(yè)車(chē)間生產(chǎn)調(diào)度很難達(dá)到最佳的排產(chǎn)效果，這樣就會(huì)造成生產(chǎn)效率低下，浪費(fèi)生產(chǎn)資源，增加企業(yè)生產(chǎn)成本。因此，用來(lái)實(shí)現(xiàn)柔性車(chē)間調(diào)度的智能算法亟需設(shè)計(jì)，進(jìn)而可以提高生產(chǎn)效率，提高企業(yè)的市場(chǎng)競(jìng)爭(zhēng)力。

柔性車(chē)間生產(chǎn)排產(chǎn)調(diào)度問(wèn)題(flexible job shop scheduling problem，F(xiàn)JSP)是傳統(tǒng)作業(yè)車(chē)間生產(chǎn)調(diào)度問(wèn)題(job shop scheduling problem，JSP)的擴(kuò)展。FJSP 這個(gè)問(wèn)題在1990年由Bruker等[2]提出，在JSP中，每道工序是預(yù)先確定的，并且其生產(chǎn)設(shè)備和生產(chǎn)時(shí)間也是預(yù)先確定的。而在FJSP中，每道工序的生產(chǎn)設(shè)備是不確定的。每道工序都有加工設(shè)備集，可在其中挑選任一設(shè)備進(jìn)行加工，并且不同生產(chǎn)設(shè)備生產(chǎn)同道工序所花費(fèi)時(shí)間不同，這增加了該類(lèi)調(diào)度問(wèn)題的靈活性，且在實(shí)際生產(chǎn)中為常見(jiàn)情況，所以解決該問(wèn)題勢(shì)在必行。

目前，解決 FJSP 的常用方法有禁忌搜索(taboo search,TS)，模擬退火(simulated annealing，SA)，遺傳算法(genetic algorithm，GA)和粒子群優(yōu)化(particle swarm optimization，PSO)等[3-6]。其中，遺傳算法因其良好的魯棒性、通用性和計(jì)算機(jī)優(yōu)勢(shì)而被廣泛應(yīng)用。武韶敏等[7]研究出了基于矩陣編碼的方法對(duì)遺傳算法進(jìn)行改進(jìn)，并且詳細(xì)描述了初始種群的生成方法。崔琪等[8]在搜索方面采用混合變鄰域的方法對(duì)遺傳算法進(jìn)行了改進(jìn)。姚麗麗等[9]提出一種啟發(fā)式正序排產(chǎn)算法，該方法采用調(diào)度規(guī)則與邏輯約束兩層改進(jìn)處理的作為總體排產(chǎn)方法。

現(xiàn)針對(duì)柔性車(chē)間生產(chǎn)調(diào)度問(wèn)題，提出一種靈活的車(chē)間調(diào)度模型，并對(duì)該模型進(jìn)行詳細(xì)的求解。針對(duì)模型結(jié)構(gòu)的特殊性，采用一種新的編碼思想進(jìn)行染色體的雙層編碼，獲得具有較高質(zhì)量和多樣性的初始種群；將MATLAB編程應(yīng)用到解碼和適應(yīng)度函數(shù)的計(jì)算中，加快求解效率和降低問(wèn)題的復(fù)雜性；給出了相應(yīng)的選擇操作設(shè)計(jì)，交叉操作采用多交叉機(jī)制，變異操作結(jié)合種群分割的思想實(shí)行兩種變異機(jī)制，進(jìn)一步改善算法的全局和局部搜索能力；并且添加檢查操作增強(qiáng)優(yōu)化過(guò)程的可行性。最后通過(guò)一個(gè)6×6調(diào)度問(wèn)題的仿真實(shí)例對(duì)算法的有效性進(jìn)行驗(yàn)證并繪制甘特圖。

1 FJSP的數(shù)學(xué)模型

1.1 問(wèn)題描述

FJSP描述如下：n個(gè)工件{N1,N2，…,Nn}在m臺(tái)設(shè)備{M1,M2,…,Mm}上加工。工件i的總工序?yàn)閚i，每個(gè)工序的順序都已確定，而且每個(gè)工件工序都有加工設(shè)備集，可挑選集合中任何設(shè)備加工該道工序，但生產(chǎn)時(shí)間因生產(chǎn)設(shè)備不同而不同。調(diào)度目的是在整個(gè)生產(chǎn)計(jì)劃中，為每道工序選擇最合適的設(shè)備，并確定每臺(tái)設(shè)備最佳生產(chǎn)順序和啟動(dòng)時(shí)間，以保證最大完成時(shí)間(makespan)最小化，總設(shè)備負(fù)荷最小和臨界設(shè)備符合最小。

1.2 數(shù)學(xué)模型

在建立FJSP數(shù)學(xué)模型之前，做出如下基本假設(shè)：①任何設(shè)備在同一時(shí)刻不能處理兩個(gè)生產(chǎn)步驟；②任一工件必須嚴(yán)格按照自己的工序順序進(jìn)行加工；③任一工件必須嚴(yán)格在自己的加工設(shè)備集里加工；④不同的工件的生產(chǎn)步驟之間沒(méi)有約束條件，優(yōu)先級(jí)相同；⑤生產(chǎn)開(kāi)始后，不能中斷，并且能正常生產(chǎn)完成；⑥設(shè)備與工件的開(kāi)始時(shí)間都允許在0時(shí)刻開(kāi)始。

為建模方便，現(xiàn)將FJSP問(wèn)題表述為：n個(gè)工件{N1,N2，…,Nn}在m臺(tái)設(shè)備{M1,M2，…,Mm}上加工。工件i的總工序?yàn)閚i，則所有工件集的總生產(chǎn)步驟為Num=sumni。上述基本約束條件下，針對(duì)最大完成時(shí)間(makespan)最小化，總設(shè)備負(fù)荷最小和臨界設(shè)備符合最小。設(shè)oij為工件i的第j道工序；M[i,j]為工件i的第j道工序的可用設(shè)備集合；

xijk為判定函數(shù)。

FJSP數(shù)學(xué)模型如下。

(1)最小化完工時(shí)間：

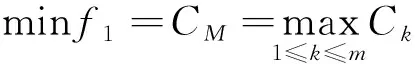
(1)

式(1)中：f1為第1個(gè)目標(biāo)函數(shù)；CM為所有設(shè)備的完工時(shí)間；Ck為第k臺(tái)設(shè)備上的完工時(shí)間；k為設(shè)備索引，k=1,2，…，m；m為設(shè)備總數(shù)。

(2)各臺(tái)設(shè)備的加工時(shí)間：

(2)

式(2)中：Wk為第k臺(tái)設(shè)備上的工作負(fù)荷；n為工件總數(shù)；ni為工件i的總工序；i、h為工件索引，i、h=1,2，…，n；j、g為工件序列索引，j、g=1,2，…，ni；Tijk為工件i的第j道工序在設(shè)備k上的加工時(shí)間。

則總設(shè)備負(fù)荷最小，即全部設(shè)備的總加工時(shí)間：

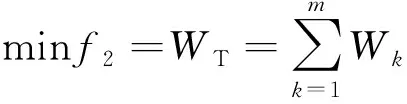
(3)

式(3)中：f2為第2個(gè)目標(biāo)函數(shù)；WT為全部設(shè)備總加工時(shí)間。

(3)臨界設(shè)備負(fù)荷，即加工負(fù)荷最大的設(shè)備：

(4)

式(4)中：f3為第3個(gè)目標(biāo)函數(shù)；WM為設(shè)備臨界負(fù)荷。

s.t.

Cij-Ci(j-1)≥Tijkxijk,j=2,…,ni;?i,j

(5)

式(5)中：Cij為工件i的第j道工序的完成時(shí)間。

[(Chg-Cij-thgk)xhgkxijk≥0]∨[(Cij-

thgk)xhgkxijk≥0],?(i,j),(h,g),k

(6)

式(6)中：thgk為工件h的第g道工序在設(shè)備k上的開(kāi)始加工時(shí)間。

(7)

Cij≤Cmax,i=1,2,…,n

(8)

Sij≥0,Cij≥0

(9)

式(9)中：Sij為工件i的第j道工序的開(kāi)始加工時(shí)間。

式(5)確保了工作順序的先后約束；式(6)限定每臺(tái)設(shè)備每次只能處理一道工序；式(7)表示可以從每道工序的加工設(shè)備集里選擇一臺(tái)設(shè)備進(jìn)行加工；式(8)限定了每一個(gè)工件的完工時(shí)間不可能超過(guò)總完工時(shí)間；式(9)限定了所有參數(shù)變量的非負(fù)性。

2 FJSP的遺傳算法實(shí)現(xiàn)

遺傳算法(genetic algorithm)是一種基于自然物種進(jìn)化規(guī)律的算法，即適者生存。遺傳算法過(guò)程如圖1所示。

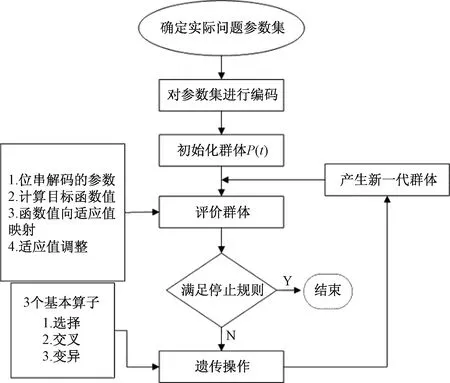
圖1 遺傳算法過(guò)程Fig.1 Genetic algorithm process

2.1 編碼設(shè)計(jì)及初始化

遺傳算法解決任何問(wèn)題的首要關(guān)鍵都是編碼，其次便是解碼，解決FJSP問(wèn)題也不例外。由于FJSP模型的特殊性，采用雙層編碼的方式，對(duì)第一層染色體編碼，為所有工件所有工序進(jìn)行排序，對(duì)另一層染色體編碼，為每道工序的加工設(shè)備編號(hào)，并最終通過(guò)MATLAB編程得以驗(yàn)證方法可行。

M{i,j}表示工件i的第j道工序的加工設(shè)備集，T{i，j}表達(dá)工件i的第j道工序被不同生產(chǎn)設(shè)備加工的時(shí)間集。假設(shè)n=4，ni=4，則M、T如表1、表2所示。

表1 M加工設(shè)備集Table 1 M processing equipment collection

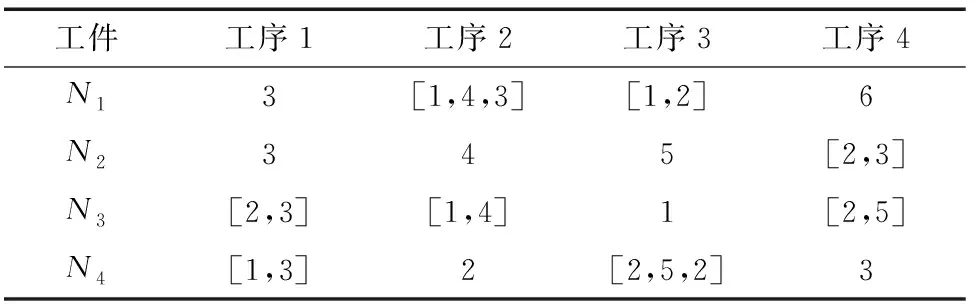
表2 T加工設(shè)備時(shí)間集Table 2 T Processing equipment time collection

兩層編碼即兩條染色體，分別命名為X、Y染色體，接下來(lái)分別對(duì)X、Y進(jìn)行編碼。

X染色體代表隨機(jī)安放每個(gè)工件的每個(gè)工序，并保證每個(gè)工件的工序的先后順序，由于n=4，ni=4，則Num=16，則X染色體長(zhǎng)度為16，X染色體編碼過(guò)程如下。

第1步將1～16隨機(jī)排序，代表所有工序隨機(jī)排列，得初始染色體{5 8 4 2 9 7 10 13 1 11 16 15 3 6 12 14}。

第2步將初始染色體{5 8 4 2 9 7 10 13 1 11 16 15 3 6 12 14}按照先后順序4個(gè)為一組進(jìn)行分組，每一組代表一個(gè)工件的4個(gè)工序，得子染色體{5 8 4 2} {9 7 10 13} {1 11 16 15} {3 6 12 14}。

第3步將每個(gè)子染色體在各自?xún)?nèi)部進(jìn)行大小排序，得子二代染色體{2 4 5 8}{7 9 10 13}{1 11 15 16}{3 6 12 14}。

第4步將子二代染色體{2 4 5 8}{7 9 10 13}{1 11 15 16}{3 6 12 14}合并成中間染色體Z{2 4 5 8 7 9 10 13 1 11 15 16 3 6 12 14}。

第5步對(duì)Z染色體中的值的位置編號(hào)，并將編號(hào)根據(jù)Z染色體1～16序列編碼數(shù)字以形成X染色體，表3中1～4表示工件1的4道工序，5～8代表工件2的4道工序，以此類(lèi)推。例如“8”在Z染色體中是第4個(gè)位置，則在X染色體的第8位置編碼為4。X染色體如表3所示。

表3 Z-X轉(zhuǎn)換表Table 3 Z-X conversion form

該編碼方式可以有效地避免工序錯(cuò)亂的情況出現(xiàn)，確保每一個(gè)工件按照各自的工藝流程加工完成，大大提高了染色體的可行性，有助于保證種群質(zhì)量。

Y染色體代表依照X染色體的工序排序，加工每道工序的具體設(shè)備編號(hào)，Y染色體編碼過(guò)程如下。

第1步依照X{9 1 13 2 3 14 5 4 6 7 10 15 8 16 11 12}順序確定可加工該工序的生產(chǎn)設(shè)備集{[M6,M8],M4,[M1,M4],[M1,M2,M3],[M8,M9],

M3,M2,M3,M7,M4,[M2,M6],[M5,M7,M8],[M2,M3],M7,M5,[M4,M6]}。

第2步將生產(chǎn)設(shè)備集內(nèi)部重新進(jìn)行編碼，得新染色體{[1,2], 1,[1,2],[1,2,3],[1,2], 1,1,1,1,1,[1,2],[ 1,2,3],[1,2], 1,1,[1,2]}。

第3步在各自的設(shè)備集中隨機(jī)挑選設(shè)備加工該道工序，最終得到Y(jié)染色體，即{1,1,2,3,2,1,1,1,1,1,2,3,1,1,1,1}。該編碼方式是為后續(xù)在時(shí)間集中采集設(shè)備加工時(shí)間提供便利。

重復(fù)以上編碼流程，直到形成完整的初始種群NP。

2.2 適應(yīng)度定義和選擇策略

選擇的目的就是實(shí)現(xiàn)適者生存，高質(zhì)量的親本遺傳給下一代。

在本FJSP模型中，目標(biāo)函數(shù)是尋求最大的完工時(shí)間的最小值，為了概率篩選，令fit=1/makespan，其中fit為適應(yīng)度，makespan為最大完工時(shí)間。makespan是根據(jù)Y染色體中選擇的加工設(shè)備而定的。Y染色體為{1,1,2,3,2,1,1,1,1,1,2,3,1,1,1,1}，依照T{i，j}對(duì)應(yīng)的時(shí)間，得TY={2,3,3,3,2,2,3,6,4,5,4,2,2,3,1,2}。

假設(shè)n=4，ni=4，定義z來(lái)表示工件i的第j道工序，當(dāng)z=1是表示工件1的第1道工序，z=2表示工件2的第1道工序，z=5表示工件1的第2道工序，以此類(lèi)推。當(dāng)z取值遍歷[1,16]后makespan的取值便得出，計(jì)算過(guò)程如下：

Tz=T{i,j}(z),z∈[1,16]

(10)

式(10)中：Tz為Y染色體在T{i,j}加工設(shè)備時(shí)間集中選取對(duì)應(yīng)加工時(shí)間。

Mz=M{i,j}(z),z∈[1,16]

(11)

式(11)中：Mz為根據(jù)X染色體選取M{i,j}加工設(shè)備集中的設(shè)備編號(hào)。

Ts=max[machtime(Mz),parttime(i)]

(12)

式(12)中：Ts為Mz和i中取最大值。

machtime(Mz)=Ts+Tz

(13)

式(13)中：machtime(Mz)為編號(hào)為Mz的設(shè)備加工第z道工序后經(jīng)歷的時(shí)間。

parttime(i)=Ts+Tz

(14)

式(14)中：parttime(i)為工件i加工完第z道工序后經(jīng)歷的時(shí)間。

makespan=max(machtime)

(15)

式(15)中：makespan為最大完工時(shí)間。

選擇采用輪盤(pán)賭選擇法(roulette wheel selection)，實(shí)現(xiàn)選擇公式Pi=fi/sumfi，其中n是種群大小，Pi是個(gè)體i被選擇概率，fi是個(gè)體適應(yīng)度值，即由各個(gè)適應(yīng)度的值在總體適應(yīng)度的比率確定。

2.3 交叉

交叉是選擇兩個(gè)親本個(gè)體，在兩個(gè)親本上選擇相同長(zhǎng)度的染色體片段進(jìn)行替換，最后重建新一代個(gè)體。根據(jù)FJSP的特點(diǎn)，設(shè)計(jì)了3種交叉機(jī)制，即單段交叉、兩段交叉和三段交叉，可提高遺傳算法的全局搜索能力，提高種群質(zhì)量，實(shí)現(xiàn)種群進(jìn)化。

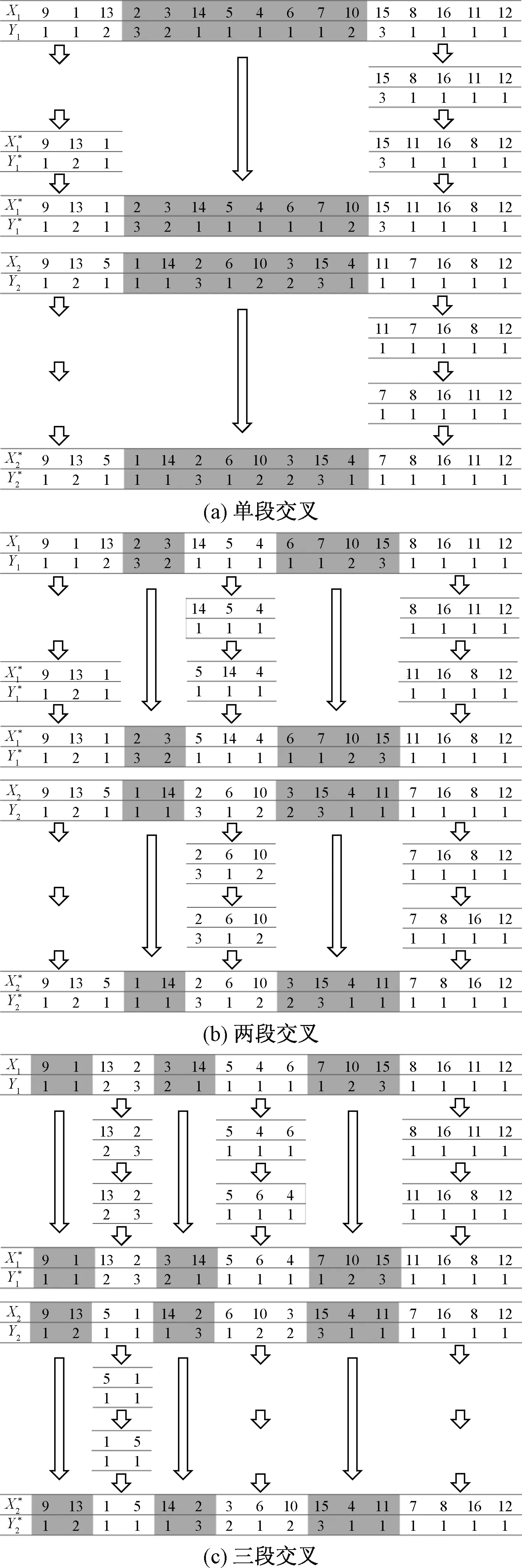
圖2 3種交叉機(jī)制圖Fig.2 Three cross mechanism diagrams

2.4 變異

變異操作也是關(guān)鍵的一步。其既可以使遺傳算法具有局部搜索能力，也可以保持群體多樣性，以防止不成熟得收斂。為了使變異操作過(guò)程具有方向性和目的性，引入了種群分割的概念[10]，基于種群分割的思想實(shí)行兩種不同的變異機(jī)制，以此來(lái)實(shí)現(xiàn)更加有效的變異操作。根據(jù)適應(yīng)度函數(shù)計(jì)算種群各個(gè)染色體的適應(yīng)度值并取種群適應(yīng)度平均值，將高于平均值的染色體定義為優(yōu)質(zhì)染色體，賦予變異概率Pm1，實(shí)行兩點(diǎn)變異機(jī)制，如圖3(a)所示；將低于平均值的染色體定義為劣質(zhì)染色體，賦予變異概率Pm2，實(shí)行翻轉(zhuǎn)變異機(jī)制，如圖3(b)所示。種群分割可以有效地避免無(wú)意義的變異，提高了遺傳算法的局部尋優(yōu)能力。

圖3 兩種變異機(jī)制圖Fig.3 Two variant mechanism dia

2.5 檢查

遺傳算法的過(guò)程中本無(wú)此操作，但由于編碼的特殊性，會(huì)在交叉和變異的流程中出現(xiàn)不可行解，如圖4中子代染色體Xnew1、Ynew1、Xnew2、Ynew2由于工序重復(fù)導(dǎo)致該染色體不能繼續(xù)遺傳給下一代并且必須被淘汰，這樣通過(guò)檢查程序的篩選，確保最終得到的最優(yōu)解符合遺傳規(guī)則，是可行的。

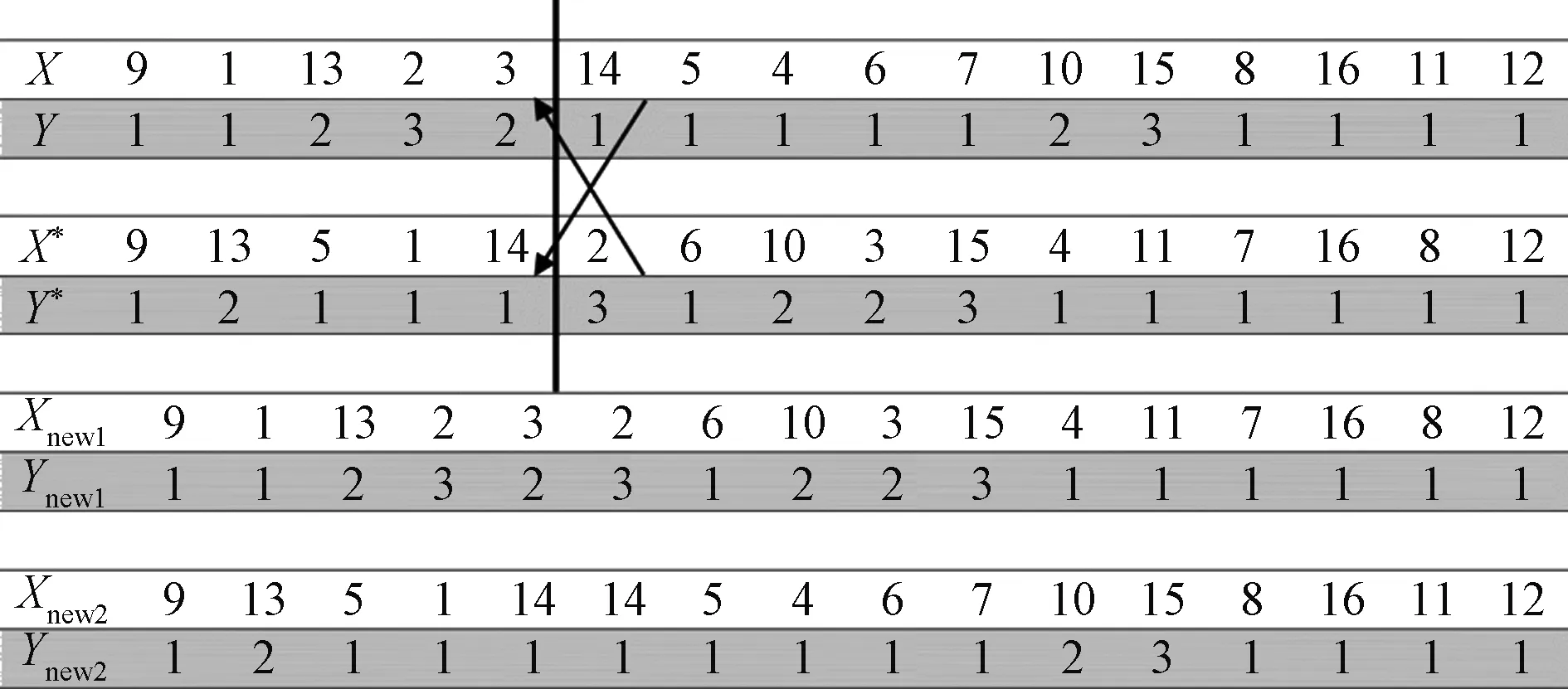
圖4 兩個(gè)父代XY交叉圖Fig.4 Two parent XY cross graphs

2.6 終止條件

通過(guò)數(shù)代后的求解，當(dāng)群體中最佳適應(yīng)度滿(mǎn)足要求，或者不再上升，即式(1)取得最小值，再或者迭代次數(shù)到達(dá)了預(yù)先設(shè)置的值時(shí)，算法停止運(yùn)行。

3 應(yīng)用案例分析

現(xiàn)對(duì)一個(gè)n=6，m=10，ni=6的FJSP進(jìn)行仿真。接下來(lái)是M{i，j}和T{i，j}，如表4、表5所示。

表4 M{i，j}加工設(shè)備集Table 4 M{i，j} processing equipment collection

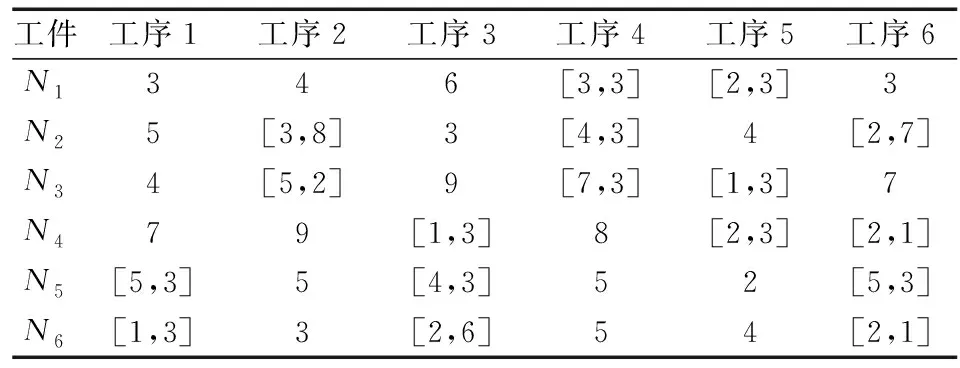
表5 T{i，j}加工設(shè)備時(shí)間集Table 5 T{i，j} processing equipment time

遺傳算法中的運(yùn)行參數(shù)為：種群大小NP=40，最大進(jìn)化代數(shù)maxgen=200，交叉概率Pc=0.8，變異概率Pm1=0.2，Pm2=0.6，代溝Gap=0.9。

基于以上技術(shù)及參數(shù)，現(xiàn)用MATLAB R2018a進(jìn)行模擬仿真，結(jié)果如圖5所示。圖5中，縱坐標(biāo)是加工設(shè)備編號(hào)，橫坐標(biāo)是加工時(shí)間，J[i，j]為工件i的第j道工序。

圖5 調(diào)度甘特圖Fig.5 Scheduling Gantt chart

經(jīng)過(guò)混合改進(jìn)遺傳算法優(yōu)化之后，與傳統(tǒng)遺傳算法方式進(jìn)行對(duì)比，在收斂速度方面有著明顯的改善，對(duì)比結(jié)果如圖6所示。

圖6 求解收斂圖Fig.6 Solving convergence

4 結(jié)論

基于JSP模型，建立了FJSP的數(shù)學(xué)模型，并采用混合改進(jìn)的遺傳算法對(duì)模型求解優(yōu)化。由于FJSP本身的相對(duì)復(fù)雜性，提出了一種新的編碼思想用于雙層染色體編碼，得到了優(yōu)質(zhì)的初始種群；算法交叉過(guò)程中只用了3種不同的交叉機(jī)制，增強(qiáng)了交叉流程的有效性；變異操作引進(jìn)了種群分割的思想，根據(jù)不同的變異概率選擇不同的變異機(jī)制；但兩層編碼結(jié)構(gòu)具有一定的特殊性，可能導(dǎo)致交叉變異之后出現(xiàn)不可行解，因此新添加檢查操作，對(duì)交叉和變異之后的不可行解進(jìn)行排除以確保種群生存能力。最后測(cè)試應(yīng)用實(shí)例結(jié)果表明該算法不僅是正確有效的，而且明顯提高了收斂速度，加強(qiáng)了最優(yōu)解的正確性。