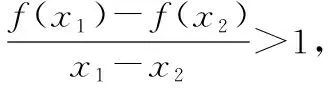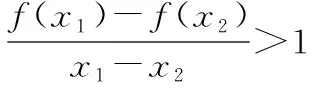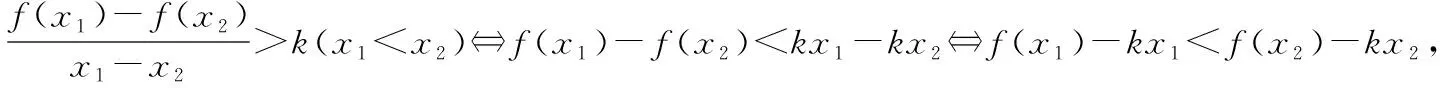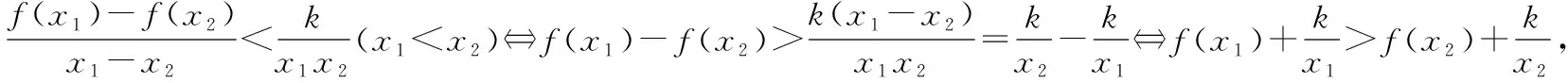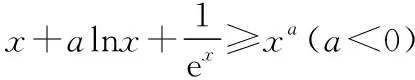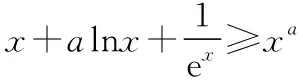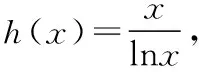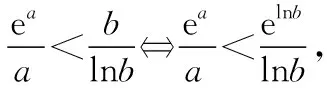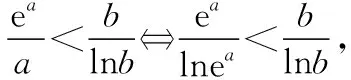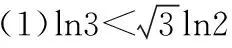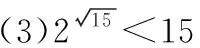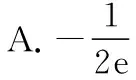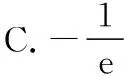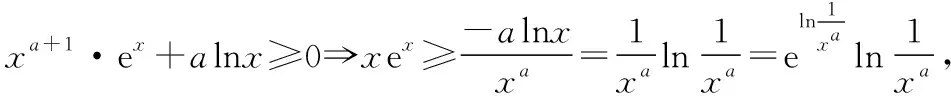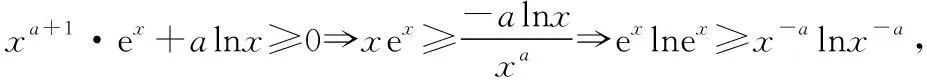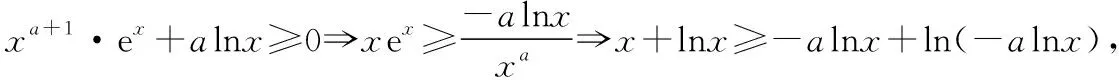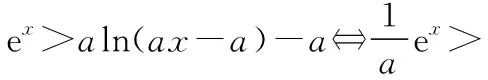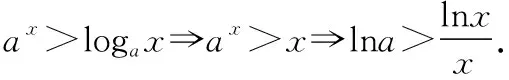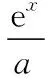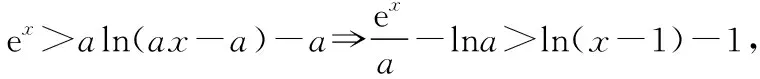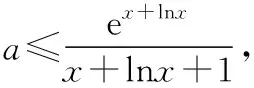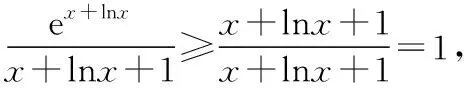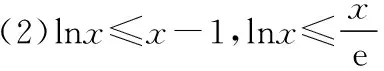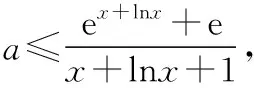揭開三道高考試題背后的“秘密”
——同構(gòu)法求解函數(shù)問題
陜西 侯有岐
一、試題再現(xiàn)與簡(jiǎn)解
題目1(2020·全國(guó)卷Ⅰ理·12)若2a+log2a=4b+2log4b,則
( )
A.a>2bB.a<2b
C.a>b2D.a 簡(jiǎn)解:因?yàn)?a+log2a=4b+2log4b=22b+log2b, 而22b+log2b<22b+log2b+1=22b+log22b, 所以2a+log2a<22b+log22b. 令f(x)=2x+log2x,由指數(shù)、對(duì)數(shù)函數(shù)的單調(diào)性可得,f(x)在(0,+∞)上單調(diào)遞增,且f(a) 題目2(2020·全國(guó)卷Ⅱ·理11文12)若2x-2y<3-x-3-y,則 ( ) A.ln(y-x+1)>0 B.ln(y-x+1)<0 C.ln|x-y|>0 D.ln|x-y|<0 簡(jiǎn)解:由2x-2y<3-x-3-y,可得2x-3-x<2y-3-y. 令f(x)=2x-3-x,由指數(shù)函數(shù)的單調(diào)性可得,f(x)在R上單調(diào)遞增,且f(x) 因?yàn)閥-x+1>1,所以ln(y-x+1)>ln1=0.故選A. 題目3(2020·新高考Ⅰ卷(供山東省使用)·21)已知函數(shù)f(x)=aex-1-lnx+lna. (Ⅰ)當(dāng)a=e時(shí),求曲線y=f(x)在點(diǎn)(1,f(1))處的切線與兩坐標(biāo)軸圍成的三角形的面積; (Ⅱ)若f(x)≥1,求a的取值范圍. (Ⅱ)由f(x)≥1,可得aex-1-lnx+lna≥1,即ex-1+lna-lnx+lna≥1, 亦即ex-1+lna+x-1+lna≥lnx+x=elnx+lnx. 令g(t)=et+t,則g′(t)=et+1>0,所以g(t)在R上單調(diào)遞增, 且g(x-1+lna)≥g(lnx),所以x-1+lna≥lnx,即lna≥lnx-x+1. 當(dāng)0 當(dāng)x>1時(shí),h′(x)<0,所以h(x)在(1,+∞)上單調(diào)遞減. 所以h(x)≤h(1)=0,所以lna≥0,所以a≥1. 故a的取值范圍為[1,+∞). 在題目1中,通過添加常數(shù)1,進(jìn)行放縮變形,使等式變?yōu)椴坏仁剑也坏仁絻蛇吘哂邢嗤膄(x)=2x+log2x結(jié)構(gòu);在題目2中,經(jīng)過移項(xiàng)變形,使不等式兩邊具有相同的f(x)=2x-3-x結(jié)構(gòu);在題目3中,經(jīng)過指對(duì)轉(zhuǎn)換、移項(xiàng)變形,使不等式兩邊具有相同的g(t)=et+t結(jié)構(gòu).然后利用函數(shù)的單調(diào)性就可以順利解決問題. 共同規(guī)律:首先將題目中的等式或不等式經(jīng)過適當(dāng)?shù)恼碜冃危硎境蓛蓚?cè)具有相同的結(jié)構(gòu),然后利用這個(gè)結(jié)構(gòu)式構(gòu)造相對(duì)應(yīng)的函數(shù),再利用函數(shù)單調(diào)性解題,我們通常稱這種解題方法為“同構(gòu)”. 研究近幾年的高考真題和模考題,可歸納同構(gòu)的常見類型和技巧如下. 類型一:地位同等要同構(gòu),主要針對(duì)雙變量 含有地位同等的兩個(gè)變量x1,x2,或x,y的等式或不等式,如果進(jìn)行整理(即同構(gòu))后,等式或不等式兩邊具有結(jié)構(gòu)的一致性,往往暗示應(yīng)構(gòu)造函數(shù),應(yīng)用單調(diào)性解決. 【感悟】(1)對(duì)于含有二元變量x1,x2的函數(shù),可以使變量x1,x2分別位于不等式兩邊,呈現(xiàn)出不等式左右兩邊結(jié)構(gòu)一樣的對(duì)稱形式,便于構(gòu)造函數(shù)模型解決問題. (2)若a≤x1 (3)含有二元變量x1,x2的函數(shù),常見的同構(gòu)類型有以下幾種: ①g(x1)-g(x2)>λ[f(x2)-f(x1)]?g(x1)+λf(x1)>g(x2)+λf(x2),構(gòu)造函數(shù)φ(x)=g(x)+λf(x); 【變式1】設(shè)函數(shù)f(x)=x2+ln(x+1). 當(dāng)x≥1時(shí),h′(x)≥0,所以函數(shù)h(x)在[1,+∞)上單調(diào)遞增. 由已知,不妨設(shè)1≤x1 類型二:指對(duì)跨階想同構(gòu),同左同右取對(duì)數(shù) 對(duì)于一個(gè)指數(shù)、直線、對(duì)數(shù)三階的問題可以通過跨階函數(shù)的同構(gòu),轉(zhuǎn)化為兩階問題解決.通常在一些求參數(shù)的取值范圍、零點(diǎn)個(gè)數(shù)、證明不等式中應(yīng)用跨階同構(gòu)來快速解題.跨階同構(gòu)需要構(gòu)造一個(gè)母函數(shù),即外層函數(shù),這個(gè)母函數(shù)需要滿足:①指對(duì)跨階;②單調(diào)性和最值易求. 當(dāng)0 所以,實(shí)數(shù)a的最小值為-e. 【感悟】指對(duì)跨階同構(gòu)的基本模式有: (1)積型:aea≤blnb,一般有三種同構(gòu)方式: ①同左:aea≤blnb?aea≤(lnb)elnb,構(gòu)造函數(shù)f(x)=xex; ②同右:aea≤blnb?ealnea≤blnb,構(gòu)造函數(shù)f(x)=xlnx; ③取對(duì)數(shù):a+lna≤lnb+ln(lnb),構(gòu)造函數(shù)f(x)=x+lnx. 說明:在對(duì)“積型”進(jìn)行同構(gòu)時(shí),取對(duì)數(shù)是最快捷的,而且同構(gòu)出的函數(shù),其單調(diào)性一看便知. ③取對(duì)數(shù):a-lna (3)和差型:ea±a>b±lnb,一般有兩種同構(gòu)方式: ①同左:ea±a>b±lnb?ea±a>elnb±lnb,構(gòu)造函數(shù)f(x)=ex±x; ②同右:ea±a>b±lnb?ea±lnea>b±lnb,構(gòu)造函數(shù)f(x)=x±lnx. 【變式2】下列說法正確的是________. 類型三:無中生有去同構(gòu),湊好形式是關(guān)鍵 對(duì)于有些式子無法直接進(jìn)行變形同構(gòu),往往需要湊常數(shù)、湊參數(shù)或湊變量(如:同乘x或同加x)等方式轉(zhuǎn)化為類型二解決. 【例3】(2019·衡水金卷)已知a<0,不等式xa+1·ex+alnx≥0對(duì)任意的實(shí)數(shù)x>1恒成立,則實(shí)數(shù)a的最小值是 ( ) 【感悟】此種類型常見模式有: (1)式子兩邊同乘x.如aeax>lnx,一般在式子兩邊同乘x(無中生有),變形為axeax>xlnx,后面的轉(zhuǎn)化同類型二(1). 【變式3】(2020·安徽六安一中模考)已知函數(shù)f(x)=ex-aln(ax-a)+a(a>0),若關(guān)于x的不等式f(x)>0恒成立,則實(shí)數(shù)a的取值范圍為 ( ) A.(0,e] B.(0,e2) C.[1,e2] D.(1,e2) 類型四:同構(gòu)放縮需有方,切放同構(gòu)一起上 對(duì)解決有些指對(duì)混合不等式問題,往往要結(jié)合切線放縮,或換元法,進(jìn)行局部同構(gòu),這樣可以大大降低這類問題的難度,但要注意取等號(hào)的條件以及常見變形等. 【例4】已知函數(shù)f(x)=x·ex-a(x+lnx+1),若f(x)≥0恒成立,則正數(shù)a的取值范圍是________. 【解析】由題意得f(x)=ex+lnx-a(x+lnx+1)≥0, ①當(dāng)x+lnx+1≤0時(shí),恒成立; 所以0 【感悟】同構(gòu)基礎(chǔ)上的切線放縮模型常見的有: (1)ex≥x+1,ex≥ex型: xex=ex+lnx≥x+lnx+1,xex=ex+lnx≥e(x+lnx); xnex=ex+nlnx≥x+nlnx+1,xnex=ex+nlnx≥e(x+nlnx). x+lnx=ln(xex)≤xex-1,x+lnx=ln(xex)≤xex-1; x+nlnx=ln(xnex)≤xnex-1,x+nlnx=ln(xnex)≤xnex-1. 【變式4】已知函數(shù)f(x)=x·ex+e-a(x+lnx+1),若f(x)≥0恒成立,則正數(shù)a的取值范圍是________. 【解析】由題意得f(x)=ex+lnx+e-a(x+lnx+1)≥0, ①當(dāng)x+lnx+1≤0時(shí),恒成立; 所以0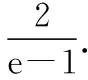
二、試題規(guī)律分析
三、常見的同構(gòu)類型及應(yīng)用舉例