探究本質 追根溯源 延展應用 提升素養
——以一道質檢試題為例

廣東 閆 偉

直線與拋物線交匯問題是高考和模考中的重點考查對象，其內涵豐富，靈活多變，具有較高的研究價值.本文對武漢市2020屆高中畢業生質量檢測試題中的第19題進行深入研究，探究試題本質，并對結論進行拓展及延伸應用，以此指導高三復習備考，實現高效復習.

1. 試題呈現與分析

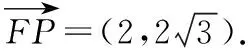
(1)求拋物線Γ的方程；

(2)已知經過點A(3,-2)的直線交拋物線Γ于M,N兩點，經過定點B(3,-6)和M點的直線與拋物線Γ交于另一點L，問直線NL是否恒過定點，如果過定點，求出該定點，否則說明理由.

試題分析：試題表面常規、內涵深刻，給人以“題在書外，根在書內”的感覺，從知識層面看主要考查拋物線的標準方程、幾何性質、直線和拋物線的位置關系及直線過定點問題，均是解析幾何中的熱點和難點；從能力層面看主要考查學生運算求解、推理論證等能力，試題較好地檢測了學生的數學素養和學習潛能.

2. 解法探究

(1) 拋物線Γ的方程為y2=4x，過程略；

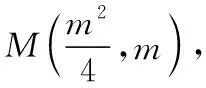
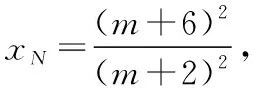
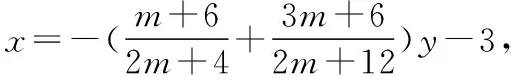
評注：本解法通過設M點坐標表示直線MA,ML的方程，進而與拋物線方程聯立得N,L兩點坐標，并求得直線NL的方程，從而得到定點坐標，解題思路清晰明了，但是運算極其繁雜，對學生的運算能力要求較高.

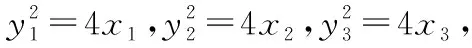
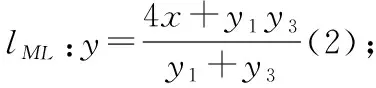
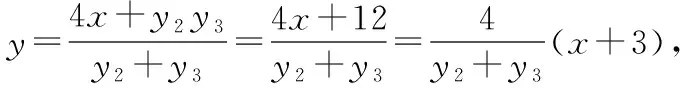
評注：本解法相對于解法1，運算量就小很多，通過求設M,N,L坐標并表示出直線MN，ML的方程，結合已知點A,B坐標求得N,L兩點縱坐標之積，這是突破本題的關鍵，雖說變量較多，只要牢牢把握N,L兩點坐標這一本質就不難得到結果，學生應重視相關結論的積累.

3 .基于GeoGebra的探究及反思

通過以上的分析和解答，得知直線NL恒過定點(-3,0)，那么該定點和題目中的拋物線參數p以及點A,B的坐標有關系嗎？如果將參數p以及點A,B的坐標一般化，定點又會是什么呢？由于涉及的運算和直線NL的直線方程較為復雜，探尋定點有一定的難度，因此筆者借助于GeoGebra平臺進行探究，通過實驗演示找到與上述參數相關的定點，同時為后面的代數證明提供更加直觀形象的思路支持.

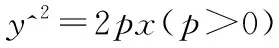
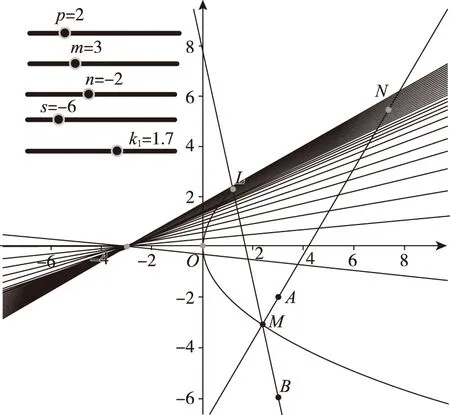
圖1

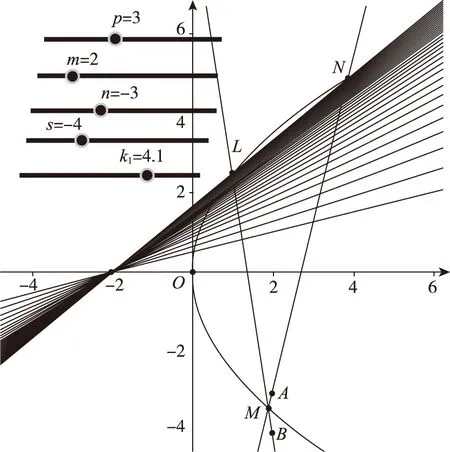
圖2

通過實驗探究可知：只有當A,B兩點的縱坐標乘積等于參數p與橫坐標m的乘積的2倍，即ns=2pm時，直線NL恒過定點(-m,0). 于是我們可以將試題結論一般化.

4. 推廣結論，揭示本質

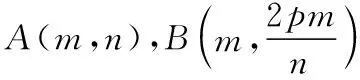
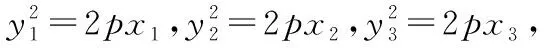
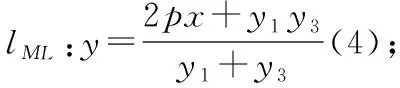
通過以上證明可知，試題條件中的A,B點似乎有些多余，因為直線NL恒過的定點(-m,0)僅僅和N,L兩點的縱坐標之積以及參數p相關，即yNyL=2pm；于是上述結論可以繼續優化.

結論2：已知拋物線Γ:y2=2px(p>0)，N(x1,y1),L(x2,y2)是拋物線上異于原點的兩個點，若滿足y1y2=2pm，則直線NL恒過定點(-m,0).

結論2的證明過程與結論1一樣，此處不再贅述. 由結論2可知，要想解決試題中直線NL過定點問題必須先要求解N,L兩點縱坐標的積，這才是試題的本質；相對于試題中先給出兩個定點A,B，再過A,B的直線與拋物線相交產生M,N,L三點，條件繁冗，干擾性較大，很多學生對于條件中諸多參變量之間的轉化關系較陌生，其根源在于沒有把握好試題的本質，對于隱藏在題目背后的意圖沒有理解到位，這就需要學生在平時重視常用結論和方法的積累，善于鉆研和思考問題的本質規律，從而提高復習備考效率.

我們在探究一個問題時應該從多角度分析，充分挖掘其潛在的價值，現對結論2進行逆向探究可以得到：

結論3：已知拋物線Γ:y2=2px(p>0)，若過點M(m,0)的直線交拋物線于N(x1,y1),L(x2,y2)兩點，則有y1y2=-2pm，且x1x2=m2.

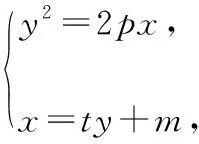
5. 追根溯源，總結提升

蘇教版普通高中課程標準實驗教科書《數學(選修2-1)》第54頁習題2.4第12題如下：

設過拋物線y2=2px的焦點的一條直線和拋物線有兩個交點，且兩個交點的縱坐標為y1,y2，求證：y1y2=-p2.

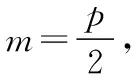
本題實質是上述質檢試題的源頭，茫茫題海，問解何處覓，課本尋根、課本探源.因此在平時的教學過程中，要學會對問題的深入探究以及對同根同源同宗問題的延續及推理.

直線與拋物線、橢圓的位置關系一直是高考和模擬考中的熱點和難點，在很多圓錐曲線題目中都是探求一些特殊結論(如定點、定值問題)，這些結論看似特殊，實則都具有普遍性，它們的背景往往是某種圓錐曲線的一個特定性質，由這些性質可以衍生出許多形式不同但本質相同的試題，研究這類試題不僅能夠更好地把握解析幾何的本質，還能擴展視野、提升解題能力以及核心素養.在平時的學習過程中，不僅要學會推理，尋找聯系，還要學會對一些結論進行整理、推廣及應用.

6. 延展應用，拾級而上

上述結論雖說不難求證，但是若能合理地運用在解決一些直線與拋物線相交的問題上，則可以減少大量的運算過程，避免繁冗的推理，實現高效解題，下面舉例說明.

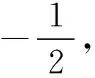
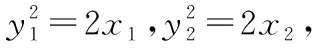
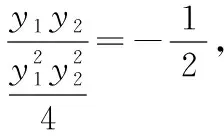
評注：本題的解題關鍵在于由斜率結果轉化到A，B兩點縱坐標的乘積為定值，再結合上述結論2鎖定直線AB恒過的定點，從而可知當直線AB與定點和原點的連線垂直時，距離最大；借助結論我們可以迅速找到問題的突破口，抓住本質，有效地降低了試題難度.

【例2】若拋物線C:y2=4x的焦點為F，過點P(2,0)的直線交拋物線于A(x1,y1),B(x2,y2)兩點，直線AF,BF與拋物線交于M,N兩點.

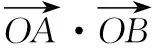
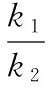
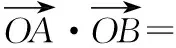
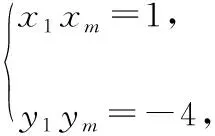
評注：由于直線AM,BN都過焦點，解題的關鍵在于借助結論3將M,N坐標關系轉化為A,B的坐標關系，從而得到兩直線斜率的等量關系式；在解題時合理使用結論能簡化推理和運算過程，具有簡潔、直觀的特點，極大地提高了解題效率.

7. 結束語

高考和模擬考中的試題大部分都是源于課本但又高于課本，結論雖然陌生，但又有據可依.因此在平時的課堂教學中，要多把教材上的知識點、例題以及練習題作為學習的第一資源，多加探究、聯想、類比、拓展,串聯一些相關的知識,讓考試回歸課本，讓解決問題變成水到渠成的事情，這樣我們的數學課堂才會更高效.