2020年新高考數學命題“新”的“告白”

浙江 余繼光 施 崢

研究2020年新高考數學命題情況，發現五新：新理念(立德樹人、核心素養、學科特色)、新評價(三大情境評價、新題型評價、不同層次評價)、新題型(數據題、多選題、結構不良題)、新應用(數學文化、最新情境、實踐能力)、新結構(整卷結構、基礎應用、科學調控)，面對新高考數學命題的五新特點，數學教學需要創新教學實踐，落實數學基本功的訓練(學會閱讀、學會運算、邏輯推理、提出問題、實驗探究、變式提升等)，提升“未來勞動者”的核心素養.

一、2020年新高考數學命題“新”在哪兒

從試題外表看，2020年新高考幾份數學試卷：北京卷、天津卷、新高考Ⅰ卷(供山東省使用)與新高考Ⅱ卷(供海南省使用)，后兩份第3，6，7，9，13，18，20(2)，21不同，但整個框架是相同的，命題專家根據各地學情采取相應命題策略，以下以山東卷為例，分析試題亮點，指導教學實踐.

1.新理念

1.1立德樹人

新高考數學命題從數學角度落實“立德樹人”的教育目標，引導學生學會“用數學眼光觀察世界”，用數學語言表達觀察，建立數學模型，解決實際情境中的數學問題，比如，第3題的志愿者服務，第5題的體育鍛煉，第15題的勞動實習等，都在充分滲透數學應用題的德育教育功能.

1.2核心素養

新高考數學命題體現2017年版2020年修訂的《普通高中數學課程標準》評價中的核心素養，比如第11題邏輯推理，第19題數據分析，第22題數學運算，第6題數學建模，第12題抽象思維，第4題直觀思維等，高考數學命題逐步進入科學評價領域.

1.3學科特色

數學學科的新高考命題有自己的特色，一是復雜的運“算”；二是智慧的“思”考；三是綜合的應“用”；比如，6道解答題的運算量都不小，雖然都是常規的基本運算，但只有運算基本功強，才能獲得成功；又如，第17題選擇性的思考，第一年不良結構命題選擇解三角形下手，還比較簡單；再如，一大六小7道數學應用題，貼近現實背景與文化背景，再加上多項選擇題中的綜合應用，可謂數學命題“應用”之天下.

2.新評價

2.1三大情境下評價

高考數學評價體系中三大評價水平：數學的情境，如第14題，考查子數列等；科學的情境，如第12題，給出信息熵的概念等；現實的情境，如第6題，新冠肺炎疫情的感染規律等，面對這些情境時，檢驗考生的“算”“思”“用”的能力.

2.2用新題型來評價

2015年教育部考試中心命題專家以新題型進入高考為課題研究結題，2020年，4道多項選擇題以特有的方式面世，第17題不良結構題給考生以多種選擇，條件開放題滲透高考數學命題之中，評價考生的發散性思維能力，以概率統計為核心的數據題也早已進入高考.

2.3不同層次的評價

設計基礎題，包括多項選擇題，檢測考生的基本功，為第一層次；設計不良結構題，檢測考生的發散性思維水平，為第二層次；設計綜合應用題，檢測考生的綜合實踐能力，為第三層次，檢驗不同層次的數學思維水平.

3.新題型

3.1多項選擇題溫柔入列

多項選擇題的引入，避免了單項選擇題的弊端——25%猜的命中率，為數學基礎和能力在不同層次的學生都提供了發揮空間，更好地體現區分選拔功能.

3.2結構不良題的選擇性

3.3未來會增加新題型

2020年新高考數學命題還處在過渡期，2015年教育部考試中心的新題型研究成果，還有舉例題、邏輯題等，在未來高考數學命題中也會逐步面世，以特有形式正式進入高考.

4.新應用

4.1數學文化滲透

了解數學文化是數學學習的任務之一，最近幾年全國卷及各地單獨命題卷，一道數學文化題成為標配，今年新高考數學命題把我國古代的一項發明：“日晷”與立體幾何的聯系挖掘出來，反映我國古代勞動人民的數學智慧.

4.2最新情境滲透

高考數學命題開始引入類似政治的“時事”題，以最新的國情為背景來命制數學應用問題，突出數學應用的教育功能，25年以來，這一特點一直持續著，2020年最新情境就是新冠肺炎疫情的傳染與傳播，第6題將病毒傳播的最核心問題編制成題.

4.3實踐能力滲透

培養中學生的創新意識與實踐能力一直是基礎教育的一大任務，第15題“學生加工制作零件”正是體現這一點，回顧立體幾何教學，引導學生制作空間圖形模型，正是在培養學生的動手實踐能力.

5.新結構

5.1整卷結構設置新

新高考卷包括單項選擇題、多項選擇題、填空題、解答題四部分，其中單項選擇題8題40分，多項選擇題4題20分，填空題4題20分，解答題部分取消了選考題內容，共6題70分，全卷總題量為22題，試卷結構逐步完善.

5.2基礎應用比例新

新高考卷數學應用題(含數學文化題)設計了六小一大共7道題，具體有科學情境、實際情境、文化情境三類，遠遠超過以前及同年其他試卷比例，強化了數學應用意識的培養，與當代科技發展環境相吻合.

5.3科學調控策略新

新高考數學命題科學調控試卷難度，貫徹了“低起點、多層次、高落差”的調控策略，發揮了高考數學的選拔功能和良好的導向作用，“低起點”體現為試卷在選擇題、填空題、解答題部分進行了系統設計，起始題部分起點低、入口寬，面向全體學生.“多層次”體現為試題的難度設計上重視難度和思維的層次性.“高落差”體現為重視數學高考的綜合性、創新性.在試題的難度設計上不僅有層次性，而且在思維的靈活性、深刻性，方法的綜合性、探究性和創造性等方面，科學把握試題的區分度，發揮數學高考的選拔性功能.

二、面對新高考數學命題教學需要創新實踐

1.落實數學基本功的訓練

不論高考數學命題改革如何進行，數學基本功永遠是數學學習的頭等大事，掌握審題基本功，運算基本功，畫圖基本功，技術基本功，策略基本功，命題基本功等，沒有這些基本功，掌握再多的方法、技巧、公式都是空中樓閣，在具體實踐或應用中都會落空.

1.1教生數學閱讀

用心閱讀數學教材是一件難事，對于高一學生教師應引導閱讀，特別是教材中的《主編寄語》《閱讀與思考》《章頭圖與章引言》等欄目，不能只是“死”刷題，通過閱讀至少使學生了解數學符號語言，文字語言，以及數學文化，幫助學生突破數學文化題.

1.2關注數學運算

引導學生對于數字計算、分數分式運算、解方程(組)、代數式變形等要達到熟練程度，數學運算要優化運算程序，把握運算方向，簡化運算過程，比如，求解下列問題：

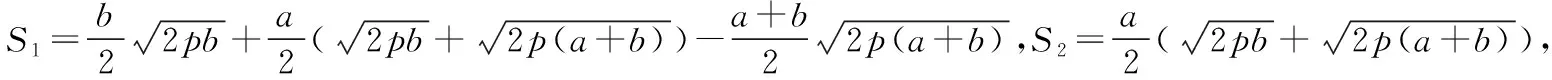
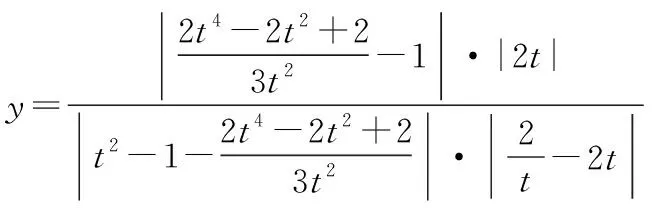
以上兩問題采自圓錐曲線問題求解片斷，學生在運算戰場上不能當逃兵.

1.3重在邏輯推理

數學教學注重邏輯推理是常識，但在概念內涵與外延、解題表達、綜合應用中真正做到不是一件容易的事，比如下列一道測試題：

問題3：數列{an}滿足a1=0.5，an=1+lnan+1，設Tn為數列{an}的前n項之積，則T2019的取值范圍是

( )

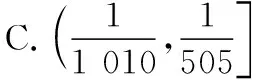
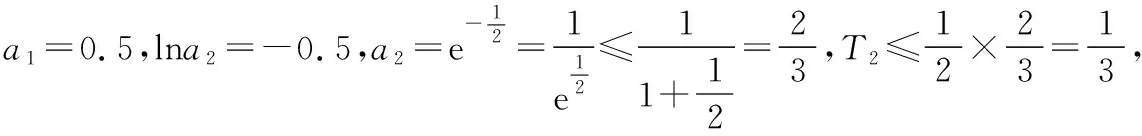
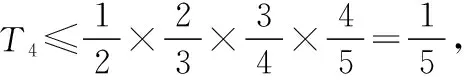
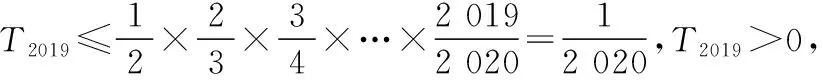
上述邏輯推理的痛點很多，一開始想直接找到通項關系式，缺少從特殊入手，尋找規律的邏輯推理意識，另外學生不了解泰勒不等式知識ex≥1+x，教學中引導學生觀察代數式結構是第一重要的事.

1.4觀察提出問題

數學實驗與應用實踐是數學教學的一個組成部分，也是很多教師的薄弱點，引領學生提出問題并解決問題是一個重要的學習方式，德國物理學家海森堡說過：“提出正確的問題，往往等于解決了問題的大半”.培養學生的數學建模意識應該從提出問題開始.從數學角度而言，學會用數學的眼光觀察自然、風光、社會、經濟等，提出有數學價值的實際問題，培養學生的數學應用意識是重要的，這體現一個人的數學應用素養，比如，下列問題探究：

問題4：羅浮宮廣場上有兩個大小不同的金字塔，如圖，有人從某個角度看，認為是一個大四棱錐與一個小四面體，于是創作了下面的數學應用題：

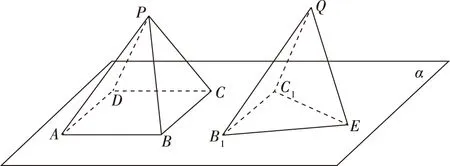
在平面α上放置一個正四棱錐P-ABCD與一個正四面體Q-B1C1E，正方形ABCD與正三角形B1C1E均在平面α上，

(Ⅰ)如果兩個幾何體的高相等，BC=B1C1，讓△QB1C1圍繞BC旋轉，當平面PBC與平面QB1C1重疊時，△PBC與△QB1C1是否重合？

(Ⅱ)BC=B1C1，讓△QB1C1旋轉，當△PBC與△QB1C1重合時，兩個幾何體構成的面數為多少？

(Ⅲ)BC=B1C1，讓△QB1C1旋轉，當△PBC與△QB1C1重合時，正四棱錐P-ABCD的高與正四面體Q-B1C1E的高之比是多少？

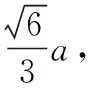
(Ⅱ)當△PBC與△QB1C1重合時，兩個幾何體構成的面數為5，因為此時△PAB與△QB1E共面，△PDC與△QC1E共面.

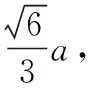
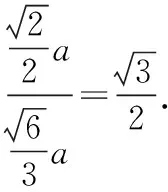
解讀：學生生活的空間內外有大量與數學相關的現象，學會觀察，學會提問題，學會提有數學意義的問題，這本身就是培養學生的數學應用意識與數學建模能力，高考數學命題專家也是通過觀察來編制數學應用問題的.

1.5變式提升思維

變式教學是數學基礎教育的一個王牌，也是提升學生數學思維的重要手段，更是解除學生思維痛點的一劑良藥，比如，二元二次方程求解是學生的一個薄弱點，對高一優秀學生設計下列問題串：

問題5：與學生一起思考下列一組解方程組問題：

經過上述解二元二次方程組的訓練后，高二求解圓錐曲線問題時就會輕松很多.

1.6養育核心素養

由具體到抽象，由特殊到一般，整個過程是學生在數學建模活動中逐步形成或養育的.比如，2019年版人民教育出版社A版數學必修第1冊，P141第13題(2)，如果學生經歷以下過程會終生難忘.

問題6：比較log23，log34，log45的大小.

變式1.比較大小：loga(a+1)與log(a+1)a，a為正整數.

變式2.比較大小：loga(a+1)與log(a+1)a，a>0，a≠1.

探究后得到的結論：

結論1.當a>1時，loga(a+1)>logaa=1，log(a+1)a

所以loga(a+1)>log(a+1)a；

然后引申到冪指數的比較：

變式3：比較aa+1與(a+1)a(a>0，a≠1)的大小.

結論4.當0

養育指導：以上問題的抽象表達是在數學探究學習中形成的概括，這一能力也是在此探尋過程中養育的.

2.增加數學應用問題教學

數學應用問題教學在某些學校還比較薄弱，數學教師怕麻煩，自1995年數學應用題進入高考數學試卷以來，教師的重視程度在不斷提升，2017年版2020年修訂的《普通高中數學課程標準》基本理念第2條中指出“提升學生應用數學解決實際問題的能力”，第3條中也明確提出“不斷引導學生感悟數學的科學價值、應用價值、文化價值和審美價值”，在學業水平與高考命題建議中也明確指出：“命題時，應有一定數量的應用問題”.

2.1不僅僅是數學應用題教學

數學應用題的教學具有兩方面的功能：一方面是數學知識應用能力的培養；另一方面是社會責任感的潛意識教育，如環境保護意識、流行病預防意識等的教育，在學科教學中滲透現代科學意識的教育，因此充分挖掘數學應用問題這一教育功能是數學應用問題教學的一個重要課題.

問題7：數學模型顯示：有關“2019—nCoV急性呼吸傳染病”的流行病調查發現，地區A新增新冠病例人數規律近似于圖形f(n)(人)(如圖，n表示第n天，12月18日記為n=0)，由于地區A的病毒攜帶者傳染到地區B，導致地區B新增新冠病例人數規律近似于f(n-14)(人)，現有下列判斷：

①1月31日地區B新增新冠病例人數達到100人；

②預測3月2日左右地區B新增新冠病例人數將進入下降趨勢；

③預測地區B累計新冠病例人數不會超過6 000人；

④預測地區B累計新冠病例人數一定不超過地區A累計新冠病例人數；

則符合上述規律的判斷有________.

問題思考關鍵是把握地區A與地區B有關新增新冠病例的規律是由f(n)到f(n—14)，只是時間推遲了14天，新增新冠病例人數并沒有變化，然后做出判斷，地區A與地區B有關新增新冠病例的規律是一致的，所以符合上述規律的判斷有①②③.

2.2提升建立數學模型的能力

2020年高考數學命題加大數學建模的測試力度，特別是根據實際情境加工的數學問題.

(Ⅰ)求橋AB的長度；

【答案】(Ⅰ)AB=120(米)；(Ⅱ)當O′E為20米時，橋墩CD與EF的總造價最低.