求解混合流水車間調度問題的離散布谷鳥算法

羅函明，羅天洪，吳曉東，陳科百

1.重慶交通大學 機電與車輛工程學院，重慶400074

2.重慶文理學院 智能制造工程學院，重慶402160

1 引言

車間調度問題是指在有限的資源條件下，如何合理地安排車間生產任務，以滿足或優(yōu)化一個或多個性能指標。該問題的性能指標種類繁多，如常用的生產效率指標[1]和近年來提出的綠色化指標[2]。混合流水車間是一種常見的流水作業(yè)生產車間，具備一般流水車間和并行機車間的特點，生產過程柔性化，更符合生產實際情況。混合流水車間調度問題（Hybrid Flow-shop Scheduling Problem，HFSP），也稱為柔性流水車間調度問題（Flexible Flow-shop Scheduling Problem，FFSP），在電子、物流及互聯網服務等現代行業(yè)都有著十分廣泛的應用，可追溯到機械、化工、紡織、制藥等傳統行業(yè)。HFSP是一種NP-hard 組合優(yōu)化問題[3]，不可能在多項式時間內精確求得最優(yōu)解，解決該問題的最佳方法是采用元啟發(fā)式算法。因此，對HFSP 的研究具有重要的實際應用價值和理論研究價值。

與一般流水車間調度問題相比，HFSP 在各道工序中存在并行機，需要同時確定工件排序和機器分配。按并行機類型的不同，HFSP可分為三類[1]：均勻并行機，指工件每道工序在任意一臺并行機上的加工時間與其加工速度成反比；相同并行機，指工件每道工序在任意一臺并行機上的加工時間相同；不相關并行機，指工件每道工序在任意一臺并行機上的加工時間互不相關，有所不同。不相關并行機上的加工時間取決于工件與機器的適配程度，更符合實際生產，同時，加工時間的互不相關性加大了求解難度，因此本文研究的是不相關并行機HFSP。

本文研究目的是針對HFSP的特性來設計一種有效的元啟發(fā)式算法，以求解該類問題，并提高解的質量和穩(wěn)定性。

2 混合流水車間調度問題

HFSP 的求解方法有精確計算、啟發(fā)式規(guī)則和元啟發(fā)式算法[4]。相對于精確計算求解時間過長，啟發(fā)式規(guī)則難以獲得全局最優(yōu)解，元啟發(fā)式算法運算速度快，所得解質量好，因而運用廣泛，如遺傳算法（Genetic Algorithm，GA）、模擬退火算法、禁忌搜索算法，新興的粒子群優(yōu)化算法（Particle Swarm Optimization，PSO）[5]、蟻群優(yōu)化算法[6]、蝙蝠算法[7]和混合蛙跳算法[8]等。王凌等[1]針對不相關并行機HFSP 提出了人工蜂群算法，采用基于多操作的鄰域搜索和隨機搜索，通過實例驗證了該算法求解HFSP 的有效性。王圣堯等[9]建立了HFSP 解空間的概率模型，進而提出了一種分布估計算法，對HFSP有著較快的求解速度。崔琪等[10]針對相同并行機HFSP提出一種變鄰域改進遺傳算法，采用NEH 啟發(fā)式算法產生初始種群，設計兩種交叉算子提高算法搜索效率。Bozorgirad等[11]提出將三種基于禁忌搜索及三種基于模擬退火的局部搜索算法與兩種基于遺傳算法的種群算法進行實驗對比，結果表明基于種群的算法比局部搜索算法在求解HFSP 時得到的解質量更優(yōu)。Santosa 等[12]針對有限等待區(qū)間HFSP，提出了一種多目標離散粒子群優(yōu)化算法。Azami等[13]針對航空航天復合材料制造系統中的兩階段HFSP，提出一種新的啟發(fā)式規(guī)則生成遺傳算法的初始種群，并在算法中設計了一種新的交叉算子。雖然對于HFSP 的求解算法已有大量研究，但是大多算法都沿用了一般流水車間調度的求解方法，即基于工件排列的編碼方法以及基于工件先到先加工和最先空閑機器規(guī)則的解碼方法。這種解碼方法易導致算法早熟，因此王芳等[14]設計了一種混合隨機概率與規(guī)則解碼方法（簡稱隨機規(guī)則解碼），擴大搜索空間，阻止算法早熟，但該方法并沒有根據HFSP的特性來設計，還有待改進和提高解的質量。

布谷鳥搜索（Cuckoo Search，CS）算法是由Yang等[15]于2009 年提出的一種新型元啟發(fā)式算法，有著算法結構簡單、控制參數少、尋優(yōu)能力強和易于結合其他算法進行改進等優(yōu)點，已被成功應用于多種工程優(yōu)化領域[16-18]。然而，CS算法應用于求解HFSP的研究較少。Burnwal等[19]基于CS算法求解以最小化延期懲罰成本和最大化機器利用率為目標的HFSP，經仿真驗證了CS算法性能優(yōu)于GA、PSO 算法；Marichelvam 等[20]通過NEH 啟發(fā)式規(guī)則生成HFSP的初始解，提高了CS算法的收斂速度；Han等[21]針對HFSP設計了自適應CS算法，并加強了算法跳出極值的能力。文獻調研表明，CS 算法在求解調度類問題時，大多數文獻都是基于某種排序映射規(guī)則將CS 算法產生的連續(xù)解轉換為離散解。該方法不能將連續(xù)解空間中全局搜索和局部搜索之間的關系有效地轉換到離散解空間，削弱了CS 算法優(yōu)越的尋優(yōu)能力。針對該方法的缺陷，陳飛躍等[22]為求解帶阻塞有差速的HFSP，提出了一種基于交叉策略的離散萊維飛行，但這種交叉策略容易產生不可行調度解，尋優(yōu)能力還有待加強。

為更好地求解不相關并行機HFSP，基于上述研究，本文所做的研究改進有：（1）設計了一種改進的隨機規(guī)則解碼方法，即基于工件數與并行機數，按概率隨機分配機器，提高了解的質量；（2）根據標準布谷鳥算法中萊維飛行和巢寄生行為兩種位置更新策略的核心思想，提出了基于位置交叉和個體距離的離散萊維飛行，設計了基于最優(yōu)插入和最優(yōu)交換的巢寄生策略；（3）結合以上兩點，在標準布谷鳥算法結構的基礎上，構建了一種求解HFSP 的離散布谷鳥（Discrete Cuckoo Search，DCS）算法，并通過實例測試和算法比較，驗證了該算法在求解質量和穩(wěn)定性方面的優(yōu)越性。

3 問題描述及模型構建

不相關并行機HFSP 一般可描述為：n 個工件都需要按照相同的h 道工序順序進行加工，每道工序有mj臺并行機(mj≥1;j=1,2,…,h)，每個工件的任意一道工序均可在該工序的任意一臺并行機上加工，且每道工序只能加工一次，已知各工件的各工序在各并行機上的加工時間，加工時間有所不同，要求確定每道工序的工件加工排序和對應的機器分配情況，使得最大完工時間最小。

因HFSP的數學模型已有豐富而完善的研究，且本文研究的是該問題的一種新的求解方法，本節(jié)參考王芳等[14]提出的0-1混合整數規(guī)劃模型，建立不相關并行機HFSP數學模型，符號定義如下：

N 為工件集合，N={1 ,2,…,n} ；

H 為工序集合，H={1 ,2,…,h} ；

M 為機器集合，M={1 ,2,…,m} ；

Mj為第j 道工序的可用機器集合：

mj為第j 道工序的可用機器數量；

i ∈N,k ∈M,t ∈N ；

Pi,j,k為工件i 的第j 道工序在機器k 上的加工時間；

Kk,t為機器k 第t 次開始加工的時刻；

Jk,t為機器k 第t 次結束加工的時刻；

Fi,j為工件i 的第j 道工序開始加工時間；

Ci,j為工件i 的第j 道工序結束加工時間；

U 為充分大的正數。

定義如下機器分配和工件排序兩個0-1決策變量：

基于以上兩決策變量構建不相關并行機HFSP數學模型如下：

目標函數（1）表示工件的最大完工時間最小化；約束（2）確保任一工件的任一道工序只能在該道工序中的某一臺機器上加工一次；約束（3）確定工件在某臺機器上加工順序；約束（4）確保一個工件只能在一臺機器上加工一次；約束（5）確保機器只能按順序加工工件；約束（6）確保機器加工任一工件的開始時刻等于該工件開始加工時刻；約束（7）和（8）確保任一工件結束加工時刻等于開始加工時刻與加工時間之和；約束（9）確保機器前一次加工結束時刻不大于后一次的加工開始時刻；約束（10）確保工件前一道工序加工結束時刻不大于后一道工序的開始加工時刻。

4 求解HFSP的DCS算法

4.1 概述

標準CS算法是一種求解連續(xù)型優(yōu)化問題的元啟發(fā)式算法，其核心思想是基于萊維飛行行為和巢寄生行為的兩種位置更新策略。萊維飛行行為是模仿自然界一些鳥類的飛行行為，可描述為一個運動體運動方向隨機，運動步長以小步移動為主，并偶爾伴有大步位移；巢寄生行為是指某些種類的布谷鳥有著具有侵略性的繁殖策略，它們趁其他鳥類（宿主鳥）外出時，偷偷在宿主鳥巢中產蛋，讓其代為孵化和育雛，而宿主鳥一旦發(fā)現了外來鳥蛋，會直接扔掉或者新建一個鳥巢。

因HFSP屬于組合優(yōu)化問題，標準CS算法的位置更新策略中具體公式已不再適用，需要重新根據HFSP 的特性設計具體位置更新策略，以保留標準CS 算法優(yōu)勢。因此，本文基于標準CS算法的核心思想，提出求解HFSP的DCS算法。

4.2 解碼方法的改進

在進行詳細的算法設計之前，需進行編碼和解碼規(guī)則的設計。因為直接利用HFSP 的數學模型求解，屬于精確計算，而HFSP是一種NP難題，在合理的時間范圍內精確計算只能求解很小規(guī)模且簡單的問題。因此，在求解HFSP 這類調度問題時，大量文獻都是根據問題描述及模型約束等，設計相應的編碼和解碼規(guī)則。這種方式既方便算法的進化操作，也方便快速獲得目標函數值以及詳細的調度方案。

本節(jié)在已有研究的基礎上，在編碼方面直接采用基于排列的編碼方法，在解碼方面基于王芳等[14]提出的一種隨機規(guī)則解碼方法，根據HFSP的特性，提出改進的隨機規(guī)則解碼方法，使得解碼方法更加合理有效，能進一步提高解的質量。

基于排列的編碼方法，其編碼序列為：

其中，n 為待加工工件數，xi∈{1,2,…,n} ，工件號xi在編碼序列中的位置代表工件第一道工序的加工順序。

解碼可分為工件排序和機器分配兩部分。原始解碼方法是按照工件先到先加工規(guī)則和最先機器空閑規(guī)則，確定工件排序時，第一道工序由編碼序列確定工件先后加工順序，后續(xù)工序的工件排序采用先到先加工規(guī)則，按照工件前一工序的完成時間排列順序，先完成的先加工，若有工件在前一工序的完成時間相同，則隨機確定這些工件的加工順序；分配機器時，將工件分配到加工當前工件所需的完工時間最早的機器上。隨機規(guī)則解碼方法是于2017 年提出的，工件排序按先到先加工規(guī)則確定，而在分配機器時，當生成的隨機概率u 大于給定的機器選擇概率Pm 時，則隨機分配機器，反之，按完工時間來分配機器。隨機概率u 服從[0，1]均勻分布，機器選擇概率Pm 選取王芳等[14]確定的0.85 概率值。由于隨機概率的存在，同一編碼序列對應的目標函數值很有可能不同，因此為獲得更優(yōu)解，設定最大循環(huán)解碼次數C，當循環(huán)過程中出現比上一代更優(yōu)的目標函數值時，則退出循環(huán)，并記為該序列的目標函數值。

表1為一個6工件、2工序的不相關并行機HFSP的加工時間表，編碼序列[2,4,3,6,1,5] 經上述兩種解碼方法所得的甘特圖如圖1、圖2 所示。甘特圖中方框內數字代表工件號，工件號自下至上出現的順序代表工序。例如，圖1 中工件2 的第1 道工序在機器M1 上加工，開工時刻為0，完工時刻為3，第2 道工序在機器M6上加工，開工時刻為3，完工時刻為7。對比圖1、圖2可知，在第2道工序給4號工件分配機器時，滿足u ＞Pm，于是將4號工件隨機分配給已加工了3號工件的5號機器。雖然最后兩者解碼得到的最大完工時間都為9，但是后者重復地將工件分配給同一臺機器，使6號機器僅在短時間內加工了一個工件，同時加大了5 號機器負荷，還有可能增大最后完工時間。

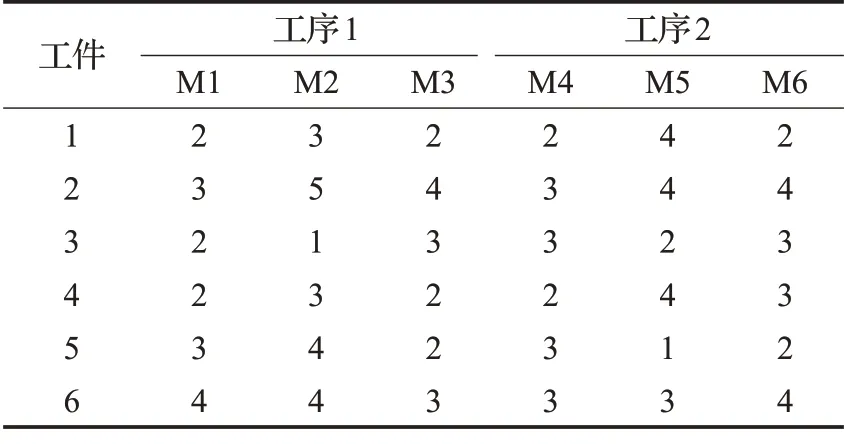
表1 加工時間表

圖1 原始規(guī)則解碼

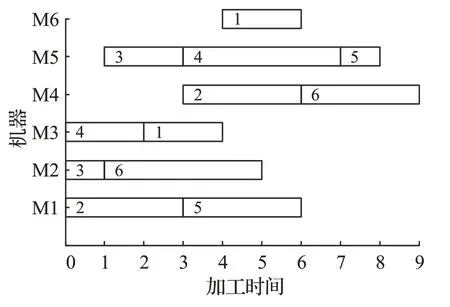
圖2 隨機規(guī)則解碼

因此，本文根據HFSP 需要同時確定工件和機器的特性，基于工件數和并行機數，對隨機規(guī)則解碼方法進行改進，提出改進隨機規(guī)則解碼方法，以提高解的質量。具體實施方法如下：工序j 中有mj臺并行機，加工任意一道工序時，每mj個工件進行一次判斷，當u ＞Pm時，任選其中一個工件對其隨機分配機器，剩余工件則以先到先加工規(guī)則確定的排序并按完工時間來分配機器，反之，這mj個工件都按完工時間來分配機器，若最后不足mj個工件但多于一個，依然按上述規(guī)則分配機器，若僅剩一個工件，則按最先機器空閑規(guī)則分配機器。對上述編碼序列用改進解碼方法求得的甘特圖如圖3所示，獲得最大完工時間為8，提高了解的質量。

圖3 改進規(guī)則解碼

4.3 離散萊維飛行的改進

在標準CS 算法中，萊維飛行是一種連續(xù)性的位置更新，而HFSP是一種典型的組合優(yōu)化問題，因而需要設計適用于HFSP的離散萊維飛行。

一般的離散萊維飛行是基于某種排列映射規(guī)則，例如最小位置（Smallest Position Value，SPV）規(guī)則[23]和最大順序值（Largest Order Value，LOV）規(guī)則[24]。SPV 規(guī)則指將實數向量中的各分量進行升序排列得到新向量，新向量中各分量所對應原來向量中的位置序列即為整數編碼序列；LOV規(guī)則與SPV規(guī)則相反，是指對各分量進行降序排列。這種方法簡單易于實現，既能保證調度解的可行性，又無須修改CS算法的進化操作，因而得到了廣泛的運用。但是，這種方法不能有效地將連續(xù)空間中局部搜索與全局搜索之間的關系轉換到離散空間，削弱了算法性能，容易陷入局部極值，難以搜索到最優(yōu)解。因此，本文提出一種基于位置交叉和個體距離的離散萊維飛行機制，種群中每個鳥巢與最優(yōu)鳥巢之間的個體距離視為概率，以這個概率進行基于位置的交叉操作。

基于位置的交叉是遺傳算法中的一種交叉策略，使用這種交叉策略可以避免在交叉操作過程中產生不可行解；個體距離是劉長平等[25]在使用離散螢火蟲算法時提出的，表示兩個體在離散空間中距離遠近程度，本文將其引入作為離散萊維飛行中的交叉概率。由于編碼序列中xi僅代表工件號，工件號之差并不能代表它們在離散空間中的距離遠近，因此本文對其稍做改進，使其更符合編碼序列之間的遠近程度，改進后個體距離求解過程如下：

首先，編碼序列的個體零點位置定義為：

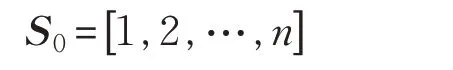
然后，編碼序列的個體位置定義為：將編碼序列X的工件號按從小到大排列，并記錄每個工件號對應所在位置，即為個體位置S。

最后，編碼序列之間的個體距離定義為：

式中，si,k、sj,k為個體i、j 第k 維的位置數；N 為分子項取值上限，按下式計算：

由定義可知di,j∈[0 ,1] ，反映了鳥巢之間的遠近程度，值越大，則距離越遠。

改進的離散萊維飛行具體實施步驟如下：

（1）計算當前鳥巢與最優(yōu)鳥巢的個體位置及兩者間的個體距離，并將后者定義為交叉概率。

（2）生成1×n 的隨機概率矩陣，將概率矩陣中每個位置的概率與交叉概率相比較，若大于交叉概率，則當前鳥巢在該位置上對應的工件號保留，反之，刪除對應該位置的工件號。

（3）將最優(yōu)鳥巢的編碼序列上與當前鳥巢的編碼序列保留的工件號相同的工件號刪除。

（4）將最優(yōu)鳥巢剩余的工件號依次填入當前鳥巢被刪除的工件號的位置。

例如，當前鳥巢編碼序列為[2 ,1,5,3,4,6] ，最優(yōu)鳥巢編碼序列為[3 ,5,2,4,6,1] 。首先執(zhí)行步驟（1），得到兩個鳥巢的個體位置分別為[2 ,1,4,5,3,6] 和[6,3,1,4,2,5] ，它們之間的個體距離為2/3，即交叉概率為2/3；然后執(zhí)行步驟（2），生成的隨機概率矩陣為[0.81,0.91,0.13,0.74,0.63,0.09] ，與交叉概率相比較，則當前鳥巢編碼序列變?yōu)閇2 ,1,x,3,x,x] ；接著執(zhí)行步驟（3），刪除最優(yōu)鳥巢編碼序列上與之保留的相同的工件號，則最優(yōu)鳥巢編碼序列變?yōu)閇 x,5,x,4,6,x] 。最后執(zhí)行步驟（4），將其依次填入當前鳥巢編碼序列中，即可得到新鳥巢的編碼序列[2 ,1,5,3,4,6] 。

4.4 巢寄生策略的設計

在標準CS 算法中，巢寄生策略的具體位置更新操作采用隨機游動方式，是一種連續(xù)的位置更新，并不適合求解HFSP這類組合優(yōu)化問題。本文根據HFSP的編碼形式特點，設計基于最優(yōu)交換和最優(yōu)插入的巢寄生策略。這兩種操作敘述如下：

（1）最優(yōu)插入操作：從編碼序列X 中隨機刪除一個工件號，得到n-1 個工件的序列X′，可知該序列有n個可插入位置，從左到右依次插入后計算新序列的目標函數值，當新序列的目標函數值優(yōu)于原序列的目標函數值時，則退出最優(yōu)插入操作，并更新編碼序列，反之，則繼續(xù)插入操作，直到達到可插入次數為止。

（2）最優(yōu)交換操作：在工件序列X 中隨機選取一個工件號，并與序列X 中其他位置上的工件一一交換，可知有n-1 次交換操作，從左到右依次交換后計算新序列的目標函數值，新序列的目標函數值優(yōu)于原序列的目標函數值時，則退出最優(yōu)交換操作，并更新編碼序列，反之，則繼續(xù)交換操作，直到達到可交換次數為止。

基于最優(yōu)交換和最優(yōu)插入的巢寄生策略可敘述為：對鳥巢i 生成一個服從均勻分布的隨機數r ∈[0,1] ，并與給定的被發(fā)現概率Pa 相比，如果r ＞Pa，則執(zhí)行位置更新操作，其中最優(yōu)插入和最優(yōu)交換操作各有0.5 的概率執(zhí)行，產生新的鳥巢Xnew；若新鳥巢Xnew的適應度優(yōu)于鳥巢

4.5 DCS算法流程及其復雜度

根據上述的求解HFSP 的算法設計思路，算法中各操作時間復雜度如表2 所示，算法總的時間復雜度為O(Gmax×PsizeChn logn)，log 的底數為大于1 的正整數，其中適應度計算和巢寄生策略都考慮最差情況。

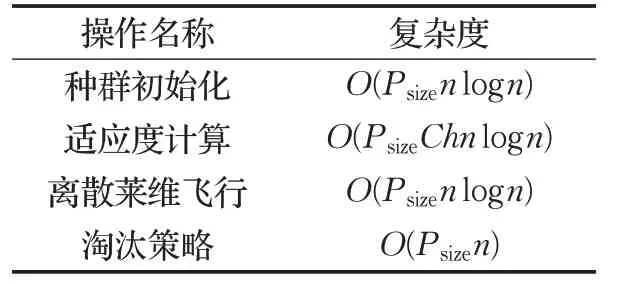
表2 算法各操作復雜度

DCS算法流程偽代碼如下所示：

1. 初始化參數：加工機器矩陣J 、加工時間矩陣T 、鳥巢種群數量Psize、被發(fā)現概率Pa、機器選擇概率Pm、解碼最大循環(huán)次數C、最大迭代次數Gmax；

2. 隨機初始化鳥巢，計算并記錄對應適應度值，記錄當前全局最優(yōu)鳥巢Xm、適應度值Fmin及具體最優(yōu)調度方案；

3. repeat 4. 采用4.3節(jié)提出的離散萊維飛行產生新的鳥巢；

5. 計算新鳥巢的適應度，若有更優(yōu)的鳥巢則鳥蛋被孵化，取代較差的鳥巢；

6. 采用4.4 節(jié)設計的巢寄生策略進行局部搜索，并記錄當前最優(yōu)鳥巢Xn、適應度值Fnew及其最優(yōu)調度方案；

7.if Fnew＜Fmin

8. Xm=Xn；

9. Fmin=Fnew；

10. 替換最優(yōu)調度方案；

11. end if

12. until滿足算法終止條件；//達到最大迭代次數Gmax

13. return最優(yōu)調度方案

5 仿真測試及分析

5.1 算法參數確定

求解HFSP 的DCS 算法主要相關參數有種群大小Psize、被發(fā)現概率Pa，解碼方法中相關參數有機器選擇概率Pm 和解碼最大循環(huán)次數C。種群大小Psize對算法影響較大，若種群數量過小，則初始化個體在解空間分布密度小，對解空間的搜索不夠徹底，并且影響種群多樣性，也易導致算法陷入局部極值；若種群數量過大，則會大大增加算法運行時間，可能會出現重復搜索某區(qū)域的現象。被發(fā)現概率Pa 主要影響算法運行時間和收斂速度，較小時，算法運行時間較長，收斂速度較快，而過小可能導致算法陷入局部極值，對于大多數優(yōu)化問題，通常取Pa=0.25，就能滿足需求。機器選擇概率Pm 直接影響算法搜索空間大小，進而影響算法收斂速度，Pm 較小，解碼過程偏向于隨機解碼，此時搜索空間較大，Pm 較大，解碼過程偏向于規(guī)則解碼，此時搜索空間較小。解碼最大循環(huán)次數C 對算法性能影響較大，C過小，難以對編碼序列進行有效的解碼，C 過大，則會過多增加算法運行時間。根據上述分析并經過大量的測試，為兼顧算法運行時間、收斂速度和優(yōu)化質量，本文中，DCS算法參數設置如表3所示。

表3 算法參數設置

5.2 改進解碼方法有效性驗證

本節(jié)分別采用原始規(guī)則、隨機規(guī)則和改進隨機規(guī)則解碼的DCS 算法（分別記為DCS_P、DCS_R、DCS_I）對5個隨機生成的算例進行求解，以驗證改進隨機規(guī)則的有效性。采用10 工件、5 工序，并行機數[3,3,2,3,3] ，加工時間[30,60] 的5 個隨機整數算例，為更好地符合實際生產，并行機處理同一個工件的同一道工序的最大時間差不得超過5。每種算法均獨立運行10次，以運行結果的最優(yōu)下界Cmax、平均值AVG、標準差STD作為評價指標，結果如表4所示。

表4 三種解碼方法的運行結果對比

從表4可以看出，對于算例1，DCS_R和DCS_I算法求解得到的Cmax分別為356和355，小于DCS_P算法求解得到的358，再對比算例2～算例5，發(fā)現DCS_R 和DCS_I 算法所得到的Cmax數值都小于DCS_P 算法，驗證了混合概率與規(guī)則的解碼方法更可能得到更優(yōu)解。然后，對算例1，DCS_I 算法求解10 次得到的平均值AVG 為355.9，小于DCS_R 算法得到的356.1，進一步看出，除算例3兩種算法10次求解的平均值AVG相同外，對算例2、算例4、算例5，DCS_I算法求解所得AVG都小于DCS_R 算法，說明改進方法提高了算法解的質量。最后，對于算例1～算例5，采用三種解碼方法求得的解的標準差STD 都小于1，說明DCS 算法的解的穩(wěn)定性好。因此，對比結果驗證了改進隨機規(guī)則的有效性。

圖4為算例1采用不同解碼方法的收斂曲線圖。可以看出，在算法前期時，DCS_P算法的收斂速度最快，但導致了算法早熟，從而陷入了局部極值；DCS_I 算法的收斂速度快于DCS_R 算法，說明改進方法能對解空間進行更為有效的搜索，從而加快算法收斂速度，進一步驗證了改進隨機規(guī)則的有效性。

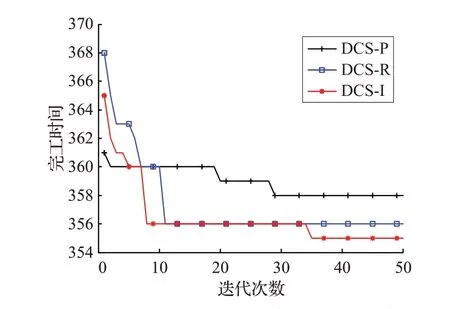
圖4 不同解碼方法求解算例1的收斂曲線

5.3 實例驗證及算法比較

本文利用王圣堯等[9]采用的兩個不相關并行機HFSP實例進行測試，并與其他文獻提出的求解算法做對比，其中SACS[21]算法為一種求解HFSP 的自適應布谷鳥算法，GA算法為常用算法，FOA[26]、EDA[9]、EDA_H[14]、IPSO[27]均為近年來求解以最小化完工時間為目標的不相關并行機HFSP 的典型代表算法。算法在Intel Core i5-7300HQ 2.50 GHz CPU、8 GB RAM、Windows 10操作系統和Matlab編程環(huán)境下編譯測試。

DCS_I 算法求解實例中兩種位置更新步驟的詳細代碼如下。

離散萊維飛行位置更新步驟的代碼：

巢寄生策略位置更新步驟的代碼：

表5、表6 為各種算法求解兩個實例獨立運行10 次的結果。

從表5、表6的運行結果可以看出，DCS_I算法對第一個實例的10次運行結果中有6次求出了最優(yōu)解23，對第二個實例10 次運行結果都求出了最優(yōu)解297。對比其他算法結果可以看出DCS_I 算法在解的質量方面優(yōu)于SACS、GA、FOA、EDA等算法，說明了本文所提算法求解該類問題的優(yōu)越性。DCS_I 算法求解結果對應的調度甘特圖如圖5、圖6所示。

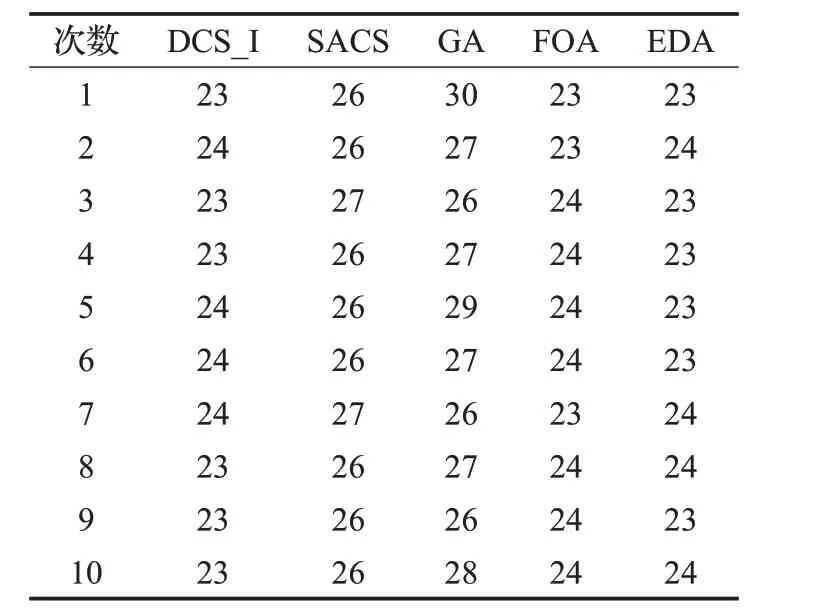
表5 實例1的運行結果

表6 實例2的運行結果

圖5 實例1調度甘特圖

圖6 實例2調度甘特圖

6 結束語

本文在不相關并行機混合流水車間調度問題的現有研究基礎上，提出了一種求解HFSP 的離散布谷鳥算法。本文主要工作如下：

（1）提出了改進隨機規(guī)則解碼方法，通過算例對比分析，驗證了改進解碼方法的有效性，能合理地加快算法收斂速度，同時增加搜索到更優(yōu)解的可能性，提高解的質量。

（2）根據標準布谷鳥算法的兩種位置更新策略思想，提出了基于位置交叉和個體距離的離散萊維飛行，設計了基于最優(yōu)插入和最優(yōu)交換操作的巢寄生策略。

（3）通過實例測試和算法比較，驗證了本文算法在求解質量和穩(wěn)定性方面優(yōu)于自適應布谷鳥算法、遺傳算法和分布估計算法等。

通過研究，發(fā)現本文算法在求解大規(guī)模問題時，用時較長，因此如何減少算法求解時間而不犧牲算法原有性能是一個未來研究方向，或者結合工程實際需要，拓展本文算法的應用領域。