基于偏相關-灰關聯方法的發動機振動影響因素分析*

翟亞浩，解夢濤，任瑞冬

(中國飛行試驗研究院 發動機所，陜西 西安 710089)

0 引 言

航空發動機振動是影響航空發動機壽命和飛行安全的重要因素[1-2]，而獲取影響發動機振動的主要狀態參數，可以合理指導飛行試驗任務的設計，最大程度地降低安全事故發生的概率。

影響渦軸發動機振動的因素眾多，包括飛行高度、速度、三向過載、姿態角等飛機狀態，發動機扭矩、燃油流量、燃氣發生器轉速、動力渦輪轉速等發動機工作狀態以及大氣總溫等大氣環境參數。有學者以某型發動機為研究對象，利用偏相關理論開展了發動機振動影響因素的相關性分析[3]，其優點在于避免了各影響因素之間的相互影響，但算法理論過于單一，容易造成誤判。另外，某些因素對發動機振動的影響是未知和不確定的，而灰色關聯分析方法[4-5]為該研究提供了新思路，它將眾多因素影響的振動現象看作一個灰色系統，可以較為真實地反映出各影響因素對考核變量影響程度。正基于此，在前人研究結果的基礎上，筆者將偏相關理論和灰色關聯方法相結合，以提高分析結果的準確性和合理性。傳統的灰色關聯度[6]分析采用的是等權計算，文中將各影響因素與發動機振動的偏相關系數作為計算灰色關聯度的權重，綜合了二者的優點，可以體現各影響因素對發動機振動的不同影響程度。基于某型渦軸發動機的試飛數據，利用偏相關-灰關聯方法進行發動機振動影響因素分析，為發動機試飛的任務點規劃提供參考作用。

1 方法原理

灰色關聯是灰色系統的基本概念之一。灰色關聯是指事物之間的不確定關聯，或系統因子之間，因子對主行為之間的不確定關聯[7-8]。

求灰色關聯度的通常包括以下步驟：確定參考序列(母序列)和比較序列(子序列)，原始數據變換，計算關聯系數，求關聯度，關聯度排序等。

1.1 確定參考序列和比較序列

根據所研究的具體問題需求，確定一個因變量因素和m個自變量因素，如式(1)和式(2):

x0=[x0(1),x0(2),…,x0(n)]

(1)

xi=[xi(1),xi(2),…,xi(n)]

(2)

i=1,2,…,m

式中：x0為參考序列；x0(n)為參考序列中的變量；xi為第i個比較序列；xi(n)為第i個比較序列中的變量。

在計算關聯系數之前需要對原始數據序列進行變換，包括將數列均值化，求差序列以及求序列的兩極最大差值與最小差值，如式(3)～(5)所示。

(1) 求各序列的均值像得：

i=1,2,…,n

(3)

(2) 求差序列，記為：

Δi(k)=|x0′(k)-xi′(k)|

Δi=(Δi(1),Δi(2),…,Δi(n))

i=1,2,…,n

(4)

(3) 求序列的兩極最大差值與最小差值，記為：

(5)

式中：x0(k)，xi(k)分別是x0及xk的第k點，其中i=1,2,…,m，k=1,2,…,n。

1.2 計算關聯系數

計算關聯系數，可以定義以下點關聯系數的計算公式，ξ為分辨系數，它可以提高關聯系數之間的顯著差異性，ξ∈(0,1)，一般取0.5。令q(X0,Xi)為xi對于x0在k點的灰關聯度(或灰色關聯系數)，可記為q0i，k點關聯系數q(x0(k),xi(k))記為q0i(k)。

q0i(k)=

(6)

1.3 權重系數確定

通過計算關聯系數可以得到比較序列和參考序列在各個點處的關聯系數值，但結果繁雜，不便于進行比較，因此需要將每個比較序列的各個點處的關聯系數值進行統計處理，并集中為一個值，即灰色關聯度。通常為反映某個比較序列與參考序列之間的灰色關聯度，是計算這兩個數據序列各個點處的關聯系數的平均值，即：

(7)

但由于各影響參數對發動機振動的影響程度不同，因此在得到各影響因素的灰色關聯度后還應賦予各影響參數不同的權重。

偏相關系數[9-10]在研究某一個要素對另一個要素的影響或相關程度時，可以不考慮其他要素的影響，單獨研究兩個要素之間的相互關系的密切程度。求解偏相關系數的一般步驟為：

(1) 計算x，y之間的關聯程度，即簡單相關系數rxy，如式(8)所示：

(8)

(2) 設一組變量x1，x2，…，xn，則由簡單相關系數rij組成的相關矩陣R：

對矩陣R求逆：

則可求得xi和xj間的偏相關系數：

(9)

將參考序列與各比較序列的偏相關系數歸一化，即可得到各影響因素的權重值；如假定變量xn為參考序列，則其余比較序列對xn的影響權重為：

(10)

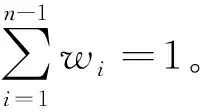
1.4 求關聯度并排序

將偏相關系數計算結果Wk作為各比較序列對參考序列的影響權重，對關聯系數求加權平均值，即：

k=1,2,…,n，i=1,2,…,n

(11)

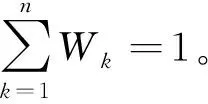
根據上式可以求得加權后的灰色關聯度值，而在關聯度分析中，關聯度值的大小實際意義并不大，而將各比較序列對同一參考序列的關聯度從大到小依次排列的關聯序起著較為重要的作用，因為它直接反映了各比較序列對同一參考序列的影響大小。

2 試驗數據分析

選取某型渦軸發動機8個架次的飛行試驗數據作為分析樣本，提取其中16個影響參數作為比較序列，包括氣壓高度、指示空速、大氣總溫、航向角、俯仰角、滾轉角以及三向過載等參數。

根據式(3)～(5)對參數序列進行均值化處理，以及求差序列，并求序列的兩極最大差值與最小差值。由式(6)，取分辨系數ξ=0.5，分別計算出各個架次中各影響因素與發動機振動量之間的關聯系數，對其分別求架次平均量，得到最終的平均關聯系數，如表1中第三列所列。

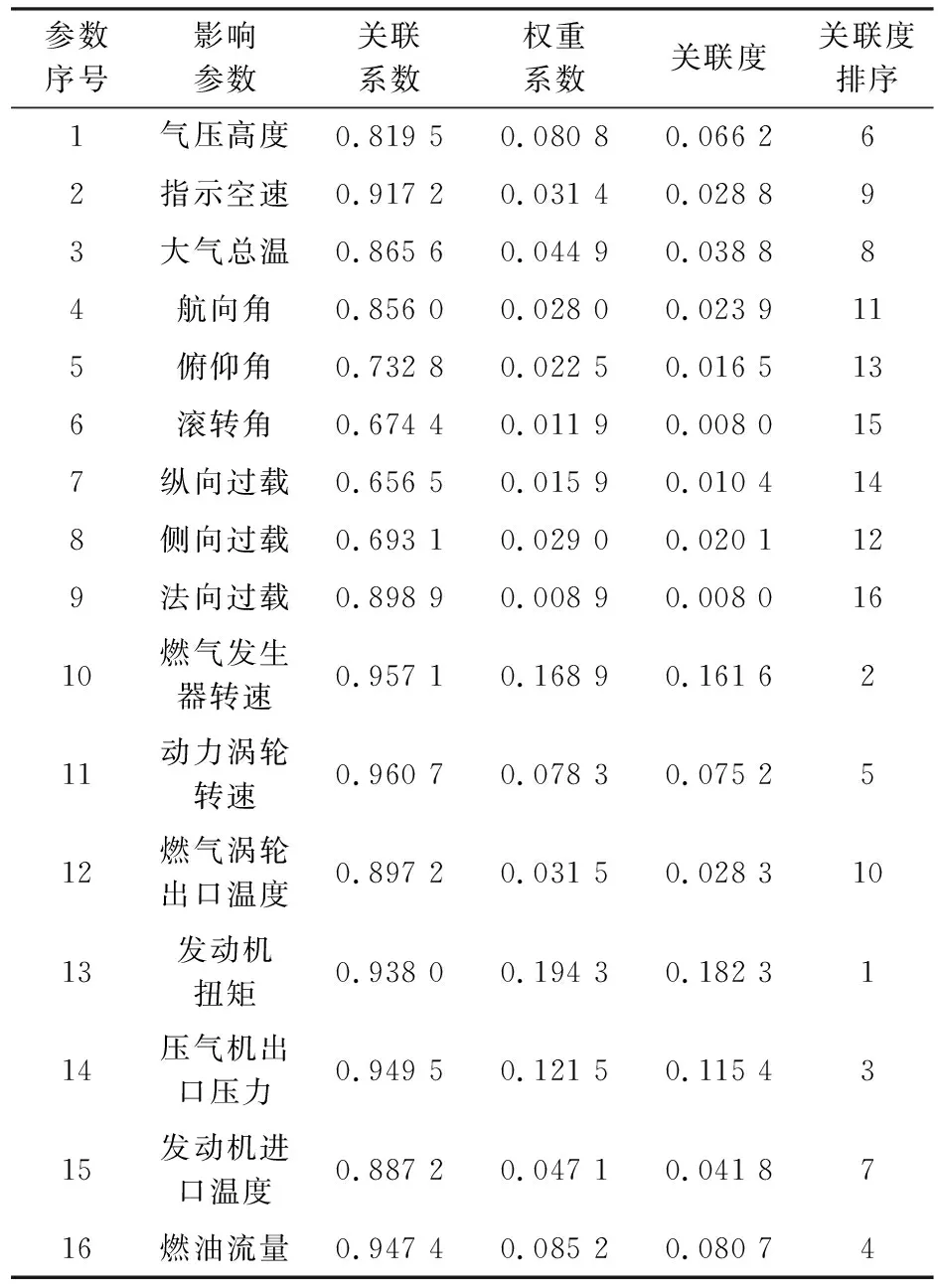
表1 發動機振動影響參數關聯度分析

根據偏相關分析原理，借助MATLAB編程分別計算得到發動機振動的各個影響因素在所有飛行架次中的平均權重系數，見表1。由式(11)可以求得各個影響因素與發動機振動間的灰色關聯度數值，然后對其進行排序，如表1所示。并根據計算結果作出發動機振動影響參數的灰色關聯度分析條形圖，如圖1所示。

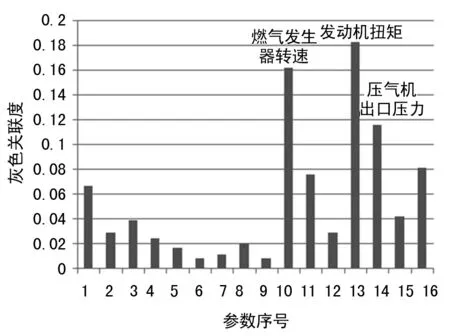
圖1 發動機振動關聯度分析條形圖

關聯度的數值大小并無實際意義，根據關聯度排序結果可知，對該型發動機振動的程度較大的三個參數依次為發動機扭矩、燃氣發生器轉速和壓氣機出口壓力，均為發動機工作狀態參數。

3 結 論

通過偏相關和灰色關聯法綜合分析的方法，將偏相關系數作為計算灰色關聯度的權重，獲得了影響某型發動機振動的各因素的關聯順序，即代表各因素在發動機振動影響中的主次關系。結果表明，影響該型發動機振動的主要因素為發動機扭矩、燃氣發生器轉速和壓氣機出口壓力等發動機工作狀態。所得分析結果對該型發動機試飛過程中任務點的合理規劃有著極為重要的意義。