探究核心素養下的《坐標系與參數方程》高考試題

甘肅 王新宏

《普通高中數學課程標準(2017年版2020年修訂)》指出高中學生學習數學應該形成數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析這六個數學核心素養；新的課程標準也是教學與考試的綱領性文件；認真探究2019年的高考數學試題，不難發現其中一些試題很好地體現了發展學生核心素養的指導思想，數學核心素養是適應個人發展和社會發展所需要的思維品質與關鍵能力；數學核心素養可以通過接受數學教育教學來形成和發展；在高考數學試題中聚焦數學核心素養符合課程改革的方向，也有利于高中數學教學回歸到育人的正確軌道上來.

在選做題中，大部分考生會選擇《坐標系與參數方程》，但2019年的高考結束之后，好多考生都說以前的高考是換湯不換藥，今年的高考是直接換了個“碗”，真是太難了，不會做，不適應；究其原因，主要是命題中心的專家們正在把高考向新課改的方向改革，關注創新，體現新課改的精神，讓高考由過去的能力為立意慢慢地向能力與數學核心素養為立意轉化，充分考查考生的直觀想象、邏輯推理、數學運算等素養.

【例1】(2019·全國卷Ⅰ·文22理22)選修4-4：坐標系與參數方程

(Ⅰ)求C和l的直角坐標方程；

(Ⅱ)求C上的點到l距離的最小值.

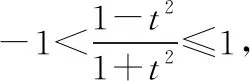
點評:這是答案匯編給出的解答,但絕大多數考生根本想不到解決問題的突破口，就被困住了,找不到好的轉換解決辦法,只好放棄；現在的高考是基于核心素養下的高考，由過去的能力立意正在慢慢地向核心素養導向轉化，徹底改變過去靠死記硬背公式、刷題搞題海戰術等低效的學習方式，要求考生深刻理解數學的本質，嘗試用數學的眼光觀察問題，用數學的思想分析問題，發展直觀想象、邏輯推理、數學運算等核心素養.

(Ⅰ)分析一：參數方程化為直角坐標系下的普通方程的常用方法有：代入消參法、平方相減消參法、三角消參法(利用sin2θ+cos2θ=1)等，但本題較新穎,直接利用這些方法都行不通，故需要冷靜思考，利用考生的直觀想象、邏輯推理素養，把問題等價轉化到能消參的軌道上去；因為參數方程中分母均為二次，分子一個為二次一個為一次，故可利用分離常數法，把二次轉化為一次，之后的消參就水到渠成、順理成章了.

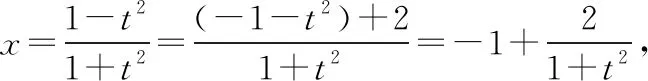
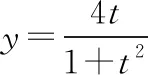
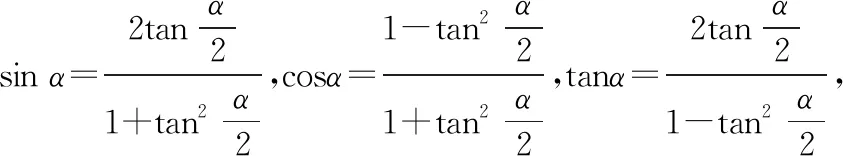
點評:①對絕大多數考生來說這題有兩個難點，一是將參數方程化為普通方程，二是x為什么不等于-1.因此，它是一道有很高區分度的題，讓搞題海戰術的考生無所適從、束手無策.但對于數學基本功特別扎實，數學素養特別靈敏的考生，就是手到擒來、輕而易舉.

②無論是學生還是教師,不能只低頭犁地,更要抬頭看課程改革這片天,現在的高考數學是緊緊圍繞在《普通高中數學課程標準(2017年版2020年修訂)》的六大核心素養下出題，所以需要從六大核心素養的角度來理解和復習高考數學；這道題主要考查了直觀想象、邏輯推理、數學運算等素養；其中邏輯推理是以具體問題為材料，文字的理解為幫手，敏銳的思考分析、快捷的反應、迅速的掌握其內在關系及核心的一種高級思維活動，是新高考主要考查的一種數學素養,所以需重視邏輯思維能力的訓練,引導學生積極拓展思維的寬度,挖掘思維的深度,提升解題能力.

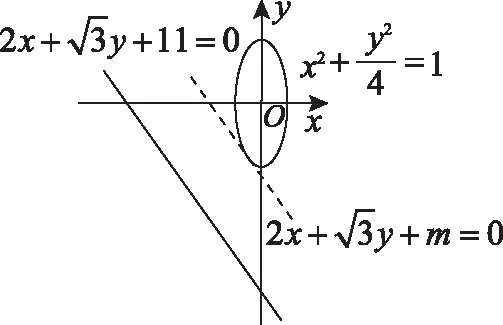
點評：利用橢圓的參數方程求最值是這類題的常規方法，但解法2利用數形結合求最值顯得更直觀、簡潔.

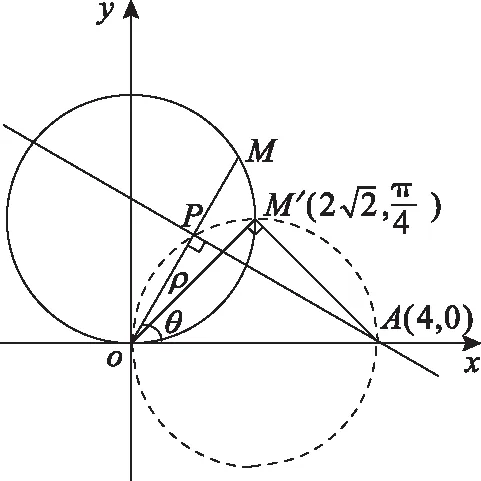
【例2】(2019·全國卷Ⅱ·文22理22)在極坐標系中，O為極點，點M(ρ0,θ0)(ρ0>0)在曲線C:ρ=4sinθ上，直線l過點A(4,0)且與OM垂直，垂足為P.

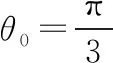
(Ⅱ)當M在C上運動且P在線段OM上時，求P點軌跡的極坐標方程.

分析：本題主要考查極坐標的幾何意義、動點的軌跡方程求法等知識，考查數形結合思想的應用，考查考生的運算求解能力和邏輯思維能力，考查的核心素養是直觀想象、邏輯推理、數學建模、數學運算.

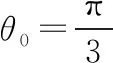
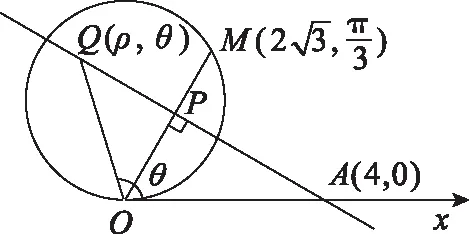
點評:① (Ⅰ)(Ⅱ)兩問直接用極坐標來做要比化為直角坐標簡單、快速得多,所以極坐標試題應打破定式思維,盡量優先用極坐標思想解題,而不是都化為直角坐標來做,這不僅是一種解題方法,更是一種優化策略、解題捷徑.

反思與建議

①警醒過度、低效的題海戰術

《坐標系與參數方程》選考題是大多數考生選做的試題，在高三的復習中，練習了大量的加減消參、代入消參、三角消參(利用sin2θ+cos2θ=1)、平方相減消參等，也練習了很多的化為直角坐標系后解決相關問題的試題，但像這樣轉換后消參，必須利用極坐標思想解決的試題幾乎沒有，所以當遇到這樣非常態的新題，考生的心理預防容易崩潰，這類新題對考生的能力要求較高,僅憑刷題已無法達到中檔題不丟分的目的,所以我們必須引以為戒,在平時的復習中,很有必要精選一些這樣的新題,讓學生學會獨立思考,勤于推理，勇于轉化,加強自我鉆研的信心與精神，形成多思多悟的自覺意識,提高思維的靈活性和批判性,促使數學學科素養在高中課堂落地生根，開花結果.

②堅持極坐標思想優先的原則

許多考生受高三復習的影響，在做《坐標系與參數方程》選做題時，多化為直角坐標系下的普通方程求解，形成了這樣的定式思維，往往就掉進了高考命題專家們為其設計的溫柔陷阱，要么運算特別煩瑣，要么根本就解不出來；大家都知道，極坐標中ρ為極徑，表示曲線上這一點與原點O之間的距離，為此與原點O有關的距離、面積或需直接寫出ρ，θ之間的關系式等問題都需優先考慮運用極坐標中ρ的幾何意義去解決它.這不僅是一種解題思路，更多時候它要比化為直角坐標運算簡便的多，是一種優化策略，可謂事半功倍.

③靈活應用等價轉化與數形結合數學思想

經過長時間的教學我們發現,數學成績高的學生相比于數學成績一般的學生主要有兩個方面的差異,一是數學成績高的學生擅長等價轉化問題,把一個外表看起來比較陌生、難的數學問題,想方設法等價轉化為我們熟悉的、容易的問題再得以解決；二是他們擅長通過畫圖，利用圖形的幾何性質解決問題，這樣不但降低了思維的難度，而且幫助構建了解題的思路，順利找到解題的切入點或突破口，看清問題的實質，減少了運算量，優化了解題的過程.所以高中數學中能畫圖的數學試題都需要畫圖，數形結合效率高.

④建立錯題本是提高成績必備的利器