對2020年一道數列不等式模考題的思考

安徽 李昭平

數列與不等式的交匯，是高考中一種常見的題型，放縮、裂項、累加常常是處理此類問題的有效途徑. 本文是筆者對2020年一道最新數列不等式模考題進行的思考與探究，旨在揭示解題思想，錘煉數學思維.

1. 題目

(Ⅰ) 確定數列{an}的單調性，并求出{an}中項的最小值；

2. 分析

3. 解答

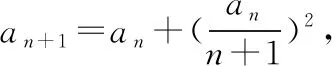
因此{an}中項的最小值是a1.

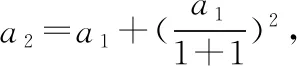
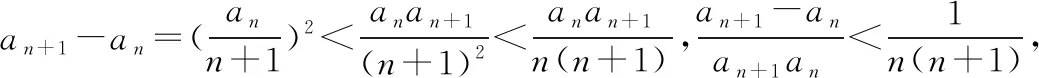
4. 結論

由上述解答，得到以下結論：對于形如an+1=an+f(an,n)的遞推式，可以通過變形為an+1-an=f(an,n)來研究數列{an}的單調性和項的最值.在無法求通項公式an時，往往可以通過適當的放縮、裂項、累加等變形和運算，確定其通項滿足的不等式，實現解題的目的.an+1=an+f(n)是an+1=an+f(an,n)的特殊情形，此時往往能求出通項公式an.

5.聯想

5.1引申聯想

適當改變模考題的結構式，作引申聯想，得到以下內容.

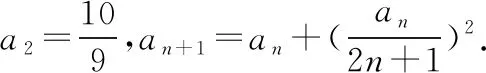
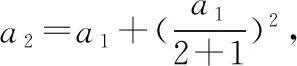
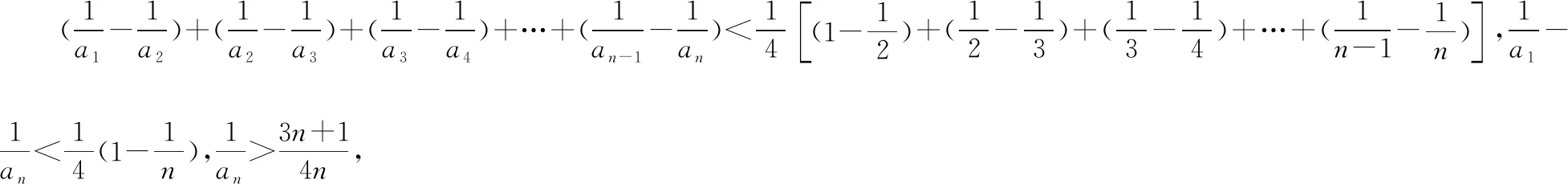
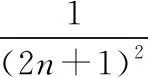
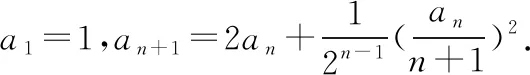
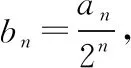
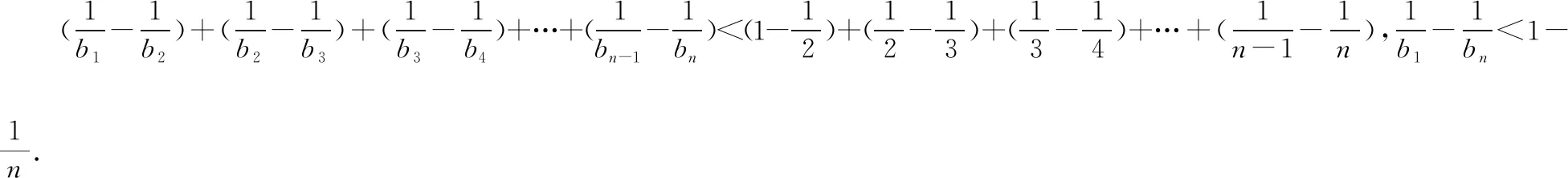
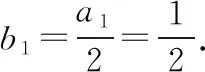
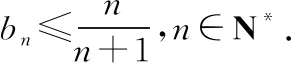
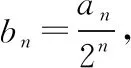
5.2逆向聯想

對模考題作逆向思考，適當互換題設條件與結論得到如下內容.

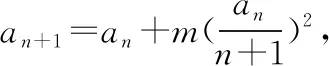
5.3 類比聯想

將模考題結構式中的“加號”向“乘號”類比，得到如下內容.

兩邊取常用對數得lgan+1≤3lgan-2lg2，即lgan+1-lg2≤3(lgan-lg2).

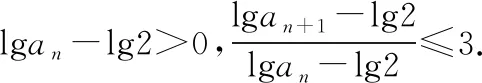
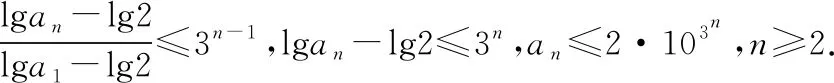
當n=1時,an=2·103n.故an≤2·103n(n∈N*).