知識定位促抓本質 整體把握助提素養
——以“平面向量雙參最值問題”為例

廣東 薛新建

著名數學家華羅庚用“由薄到厚”和“由厚到薄”兩個基本過程，形象地解釋了知識框架和解題訓練之間的辯證關系.“由薄到厚”是學習接受、加強積累、構建知識框架、奠實“四基”的過程；“由厚到薄”則是消化提煉、探索本質、回歸知識框架、提升“四能”的過程.波利亞在《怎樣解題》中把解題的第一步制定為“弄清問題”，即對問題產生的知識背景進行精準定位,用知識框架的整體視角看待問題，再對題目的條件和設問，從不同角度關聯運用相關知識，進行有目標的轉化.于濤老師認為，解題的核心就是知識的聯系與模型的識別.正確的解題訓練可以發掘知識之間隱含的關聯性，使知識框架進一步強化和完善，并提高數學模型的適用性.解題的出發點和落腳點回歸知識本身，才能引導學生把握數學內容的本質，形成和發展核心素養，符合《普通高中數學課程標準(2017年版2020年修訂)》(下稱“新課標”)的基本理念.

下面就以平面向量“雙參最值問題”為例，對高三解題訓練的高效模式進行探究.

一、典例引入，定位剖析

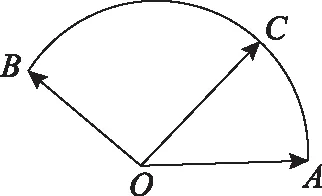
這是一道經典的向量高考原題，2017年全國卷Ⅲ還將相同問題以圓的形態再次考查.平面向量作為高中數學重要的工具性內容，兼具數形兩種形態，與其他章節例如三角函數、解析幾何、立體幾何、參數方程等知識都有交匯，是高考考查的熱門考點.本題以極具數學之美的幾何圖形扇形作為背景，以簡潔精煉的向量符號形式給出條件，形數兼備，又引出二元函數最值問題，借以考查函數思想.題目涉及向量知識模塊如相等向量、向量運算、向量坐標等基礎知識，和其他知識模塊如基本不等式、線性規劃、解三角形等初等知識，并可引申出拉格朗日乘數法等高等知識，豐富的知識面跨度，給不同層次的學生提供了足夠的發揮空間.題目體現的消元、化歸與轉化、函數與方程等數學思想和方法，以及考查的邏輯推理、數學建模、數學運算、數學抽象等諸多核心素養，都具有極高的推廣和研究價值.

定位1【向量運算】條件是向量表達式，問題是兩個實數和的形式，回顧向量知識框架中，哪一部分可以實現向量向實數的轉化？不難想到向量的運算中，求數量積或者求模(平方)，都可以將向量關系實數化，為本題提供突破思路.

定位1.1【向量求數量積】如圖，設∠AOC=α，則

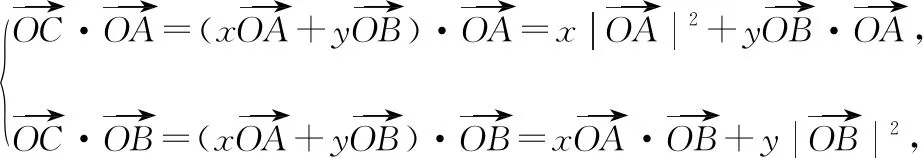
至此完成向量關系實數化，由于α的引入，得到的x和y的關系屬間接關系，即參數方程關系，只需通過消元將二元函數最值問題轉化為一元函數最值問題即可解決問題.

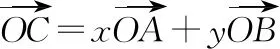
定位2【二元函數最值問題】從函數知識模塊中提取出如圖所示的解決二元函數最值問題的基本方法框架，由于題中x，y的等量關系消元和畫圖比較困難，本題優先選用基本不等式進行計算.

定位2.3【拉格朗日乘數法】高等數學里的拉格朗日乘數法能夠把約束優化問題很好地轉化為無約束優化問題，這里可以根據學生基礎加以引申，也可以點到為止為學生將來進入大學學習高數預留伏筆.

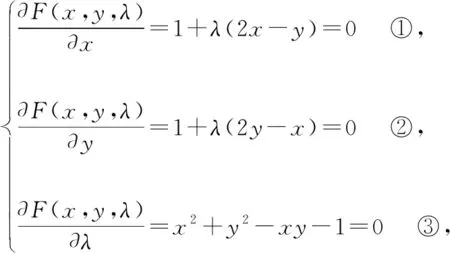
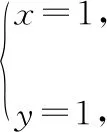
定位3【相等向量的概念】條件中的向量表達式可以看作一個向量的等量關系，“相等向量”從屬于向量的基本概念知識板塊，其具有幾何和代數(坐標法)兩種基本形態，能不能從中找到系數間的等量關系呢？利用代數(坐標法) 形態可以達到這個目的.

定位3.1【相等向量的坐標形式】如圖，以O為坐標原點，OA為x軸正半軸建立平面直角坐標系，

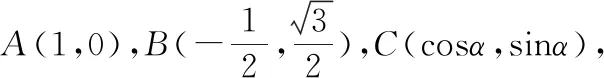
② 設a=(x1,y1),b=(x2,y2)，則a±b=(x1±x2,y1±y2)；λa=(λx1,λy1)；a//b?x1y2-x2y1=0；

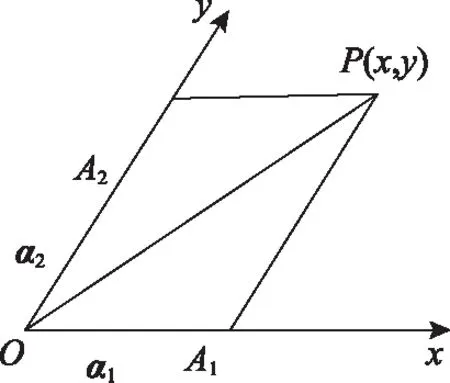
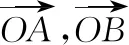
斜坐標系是對直角坐標系進一步的推廣，由于建系要求低而具有廣泛的適用性.在斜坐標系下向量表達式坐標化后實現實數化的目標，思路清晰、計算簡潔，再借助線性規劃的思想方法解決最優問題，在平面向量雙參最值問題與一般的二元函數最值問題間搭起了一座新的橋梁.實際上，斜坐標系可以方便地解決兩個實系數x,y任意線性組合的最值問題，只需要根據題目調整一下基底即可.

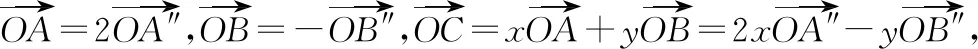
二、形成框架，提升思維

通過前述思考我們發現，平面向量雙參最值問題可以定位到平面向量知識模塊中的“向量運算”、“相等向量”和“坐標定義”三個小的知識點.“向量運算”中的“數量積”以及“模”的計算，都可以實現向量關系實數化，從而將平面向量雙參最值問題轉化為二元函數最值問題，二元函數最值問題從屬于函數知識模塊，具有自身的一套解決體系，因此后續思路按照二元函數最值問題的方法框架就可以推進下去；“相等向量”概念的代數形式(坐標化)則把題目條件導向二元函數最值問題的下一步，即“探尋二元等量關系”；“坐標定義”的問題定位引發我們對斜坐標系的引入，使得問題直接轉入廣義規劃解決問題，這符合二元函數求最值問題下屬的一種具體情況.通過上述思考，我們將平面向量雙參最值問題在向量和函數兩個知識模塊之間做如下架構.

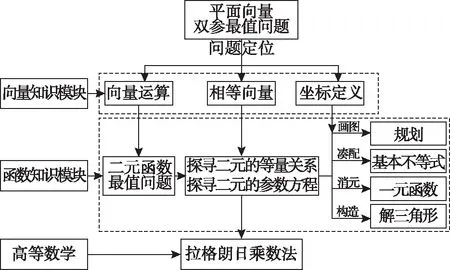
三、推而廣之，反思教學

上述對數學問題的探索模式在高三復習中具有很大的推廣價值，具體說來有如下實際意義：

將問題在知識框架中定位可以促進學習者看清其數學本質.數學問題千變萬化，問題的解法多種多樣，如果教師只是就題論題或者就題論法，必然會陷入無限題海，失去方向.如果學習的過程中能夠將問題回歸知識框架，以有限的知識框架去界定無限的問題類型，就可以從不同的視角對問題進行剖析，最終看清問題的本質，實現問題的“歸一”.

用知識框架統領解題訓練，學習者才會有思維的提升.知識框架具有系統性、遠見性和可發展性，將平時的解題訓練建立在知識框架之上，學習者才能理解巧妙思路的來源，激發尋找更多思路的靈感，實現思路之間的優劣比較從而實現思維的提升，進而對知識框架進行完善和重構，使知識框架得以補充和發展.而忽略知識框架，片面追求兵來將擋水來土掩式的解題訓練，則會把知識碎片化，即使短期內頗具效果，從長遠來看，會把數學的學習變成機械教條的死記硬背，學習者缺乏思維的訓練和提升，感受不到數學的美感和成就感，漸漸也會失去學習的興趣.