借教材，拓思維
——數列教學的實踐與思考

云南 段朝龍

在我們的實際教學中，教材上概念、公式、例題及習題的教學是我們整個數學教學活動的核心，教材也是學生思維拓展和能力培養的主要載體.因此，應充分理解和把握教材，充分挖掘教材所蘊藏的思維方法，同時認真研究課本相關知識的來龍去脈，對例題、習題進行深度剖析，對典型的問題，需要從多個角度挖掘其蘊含的思維價值，并結合學生的實際加以適當的構造和拓展，努力引導學生學以致用，這樣才能更好地提升教育教學質量，才能更好地培養和發展學生的數學思維．

美國教育家蘇娜丹戴克說過:“告訴我,我會忘記,做給我看,我會記住,讓我參加,我就會完全理解.”因此在實際教學中，我們一線教師更重要的應該是培養學生獨立思考和鉆研的習慣和能力，激發學生的發散性思維和創造性思維.

著名的教育家葉圣陶曾說過：“教材只能作為授課的依據，要教得好，使學生受到實益，還得靠教師的善于應用.”“問題是數學的心臟.”學生的數學學科核心素養是在學生與情境、問題的有效互動中提升的.在實際教學過程中，我們不難發現很多知識可以在問題中直接使用，但也有很多知識、思想、方法隱藏在教材例題、習題的背后.而且歷來高考命題都非常重視回歸教材，回歸課本，正所謂追本溯源，故而我們一線教師在實踐過程中，更應該真正尊重教材，研究教材、拓展教材和活用教材，深度體會和掌握知識形成的思維過程.進一步探求例題、習題背后蘊藏著的教學價值，對相關內容進行總結、再造和升華，真正使例題、習題成為我們獲取知識、拓展思維、提升能力的又一個重要載體．而且課本中很多例題、習題都非常具有典型性和可研性，是我們教育教學中真正的精華.我們應對這些問題進行充分的探究和拓展，激活教材，融會貫通，提高師生的鉆研意識和研究能力，更好的發展學生思維和提升教學質量．

本文的核心即就數列教學中如何借用教材對學生進行思維拓展，如何挖掘教材例題、習題的應用價值和思維價值，談一點自己的實踐感受和思考．

一、借用教材的相關推導和演示.理解知識的生成過程，進而引領學生進行歸納和探究，激發學生的內部動機和興趣，培養學生的研究欲望.

【例1】等差數列前n項和公式是什么？怎樣推導的？高斯算法的妙處在哪里？再想一想還有其他推導方法嗎？(人教A版,數學必修5第二章數列第42頁探究)

證明：∵Sn=a1+a2+a3+…+an.① ∴Sn=an+an-1+an-2+…+a1.②

①+②得2Sn=(a1+an)+(a2+an-1)+(a3+an-2)+…+(an+a1).

讓學生充分體會高斯算法的巧妙之處，進而采用倒序相加法推導等差數列前n項和公式.通過合作探究，激發學生的內部學習動機，努力解放思維禁錮，引發學生思考，激發學生發散性思維，并引導學生繼續尋找等差數列前n項和公式的其他推導方式.

思維拓展1：深刻理解前n項和的含義和等差數列的通項公式，活用等差數列的通項公式構造新的推導方式，從而增強學生對相關知識的理解和應用，培養學生積極思考的習慣，讓學生體會到研究的樂趣.

證明：∵Sn=a1+a2+…+an=a1+(a1+d)+(a1+2d)+…+[a1+(n-1)d].

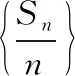
【例2】等比數列前n項和公式是什么？怎樣推導的？再想一想還有其他推導方法嗎？(人教A版，數學必修5第二章數列第55頁)

證明：∵當q≠1時，Sn=a1+a2+…+an=a1+a1q+a1q2+…+a1qn-1.

∴qSn=a1q+a1q2+a1q3+…+a1qn.

當q=1時，Sn=na1，故而得證.

∴Sn=a1+a2+…+an

思維拓展1：充分理解等比數列的通項公式和前n項和的定義，直接改寫相關各項，并進行適當化簡、變形與再造，從而歸納出下列方式進行推導.

證明：∵當q≠1時，

Sn=a1+a2+…+an

=a1+a1q+a1q2+…+a1qn-1

=a1+q(a1+a1q+…+a1qn-2)

=a1+q(a1+a2+…+an-1)

=a1+qSn-1=a1+q(Sn-an).

當q=1時，Sn=na1，故而得證.

思維拓展2:由于注意到思維拓展1中Sn=a1+qSn-1，聯想到遞推公式的特定式，從而構造新的等比數列，從而又可挖掘出新的證明方法——待定系數法.

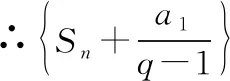
當q=1時，Sn=na1.故而得證.

思維拓展3：充分理解和應用等比數列的定義，引導學生思考與聯想，并對方程進行適當的整理、歸納和改寫，從而借用“等比性質”來證明.這樣既能較好地帶動學生進行思維活動，又能較好地培養學生的化簡和變形能力.

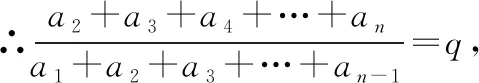
當q=1時，Sn=na1.故而得證.

在我們平時的教學實踐中，對一些概念和公式進行必要的探索和挖掘，從不同角度分析其特性，引導學生對相應的式子進行必要的化簡變形、整理歸納和比較發現，并積極聯想和遷移，從而把一些孤立呆板的知識轉化為有助于學生認知和把握的理性知識，這樣會讓學生更加深刻地體會到對知識的理解、應用和研究的樂趣，也讓學生學會抓住問題的本質，提高他們舉一反三的思維能力，進而培養學生對未知的探索能力．

二、再度借用教材例題、習題及變式題進行探究發現，培養學生分析問題和解決問題的多元思維.讓學生真切感受這種自我探索、自我發現的學習方式，并在例題習題中體會和品嘗新知的研究過程，從而形成對數學知識不斷求索的自我需求.

思維拓展1：緊扣a,b,c成等差數列這一條件，借用等差中項法進行直接推導.讓學生體會數學問題解決的精髓——“看見已知想性質，看見結論想判定”.

證明：設a=b-d，c=b+d.

思維拓展2:充分理解數列是函數特例這一性質，從而應用數列的函數特征進行推導，這其實是最能揭示其本質的一個證明，同時也能使學生對知識有一次升華的體驗.

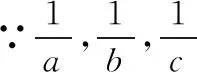
【例4】(教材習題變式訓練)已知{an}是等差數列，Sn是其數列{an}的前n項和，S5=28,S10=36,求S15.

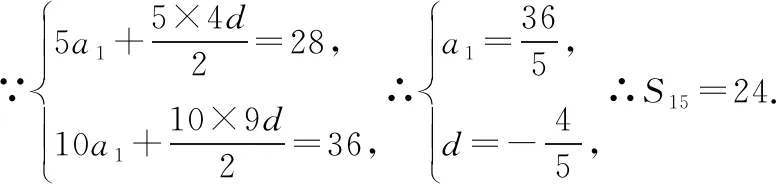
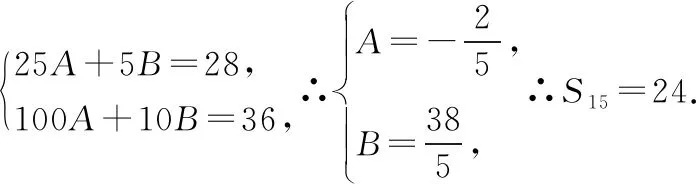
思維拓展1：結合等差數列前n項和公式的函數特征，采用待定系數法進行求解.這樣能使學生在認識上實現跨越，并能培養學生函數、方程數學思想的應用意識，使相關知識得以提升.

思維拓展2：引導學生認真觀察與分析，發現可用等差數列的性質:“等差數列中，Sn,S2n-Sn,S3n-S2n,…，成等差”，從而采用“等項片段和”直接計算出S15.

解：∵S5,S10-S5,S15-S10成等差數列.∴S5=28,S10-S5=8,S15-S10=-12.

∴S15=24.

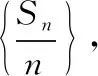
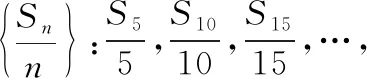
思維拓展4：受思維拓展3的啟發，可采用數列的函數特性，應用函數“圖象法”來解決，真正理解和應用數列的函數特征.從而使知識再次升華.

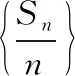
∴從而S15=24.

這樣，表面上看起來十分簡單的一道題，經過不斷探索發現，將數列與函數等知識充分融合，產生了多種有價值的解法.在這樣一個探索過程中，學生的思維會得到充分地釋放，在交流與展示過程中，也更能促使學生對相關知識有本質理解和綜合應用,從而有效的提升學生的認知和鉆研精神.

三、借用教材例題和習題的解法，尋求知識間“共性和個性”的關系，培養學生的思維遷移，使學生學會“反思性學習”和“創造性學習”，促使學生學會獨立思考、遷移發散和綜合應用.

解法反思：我們可以帶領學生積極總結和歸納,找出裂項過程的共性和個性，發現裂項相消在不同形式下的相消規律，理解裂項相消與相關參數的關系，體會相鄰項的裂項相消和隔項的裂項相消在解決問題中的技巧.

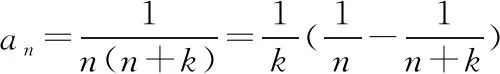
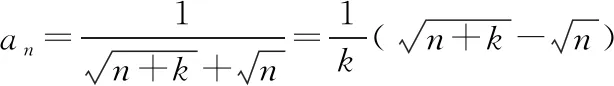
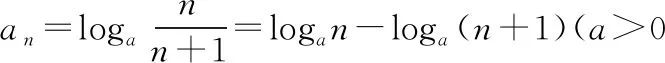
四、結束語

教材中像這樣可以進行深入探索和拓展的題目還有很多，只要學生形成良好的研究習慣，善于鉆研與反思，學會從不同角度不斷發散和引申，可以總結出很多很好的方法和技巧，有助于學生進行更高效率的學習，真正提高學生分析問題和解決問題的能力，更好的培養學生的數學核心素養．