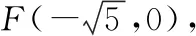盤點直線參數方程的主要應用

黑龍江 王榮峰

直線參數方程是普通高中課程標準實驗教科書的重要內容，主要應用在求線段的長度、求距離的乘積、求直線的方程、求參數的取值、求參數的范圍、求分點的坐標、求中點的軌跡和求面積的最值等問題中.

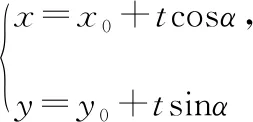
1.求線段的長度

( )

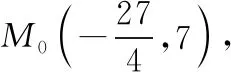
A.1 B.3

C.4 D.5

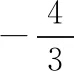
點評本題也可寫出直線l的點斜式方程，并與雙曲線的方程聯立，進而求出M點的坐標，最后由兩點間距離公式來求解，但借助直線參數方程，利用參數t的幾何意義來處理更顯簡潔清晰.

2.求距離的乘積

( )

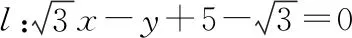
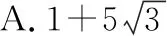
C.1或4 D.非上述答案

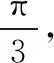
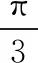
3.求直線的方程

( )

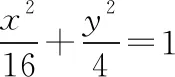
A.x+2y-4=0 B.x-2y-4=0

C.2x-y-3=0 D.2x+y-3=0

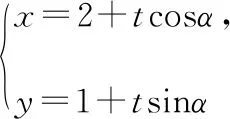
點評因為點M是線段AB的中點，由直線方程中參數t的幾何意義可知t1+t2=0，于是便可求得tanα的值，進而找到了解決問題的突破口.

4.求參數的取值

例4.經過拋物線y2=2px(p>0)外的一點A(-2,-4)，且傾斜角為45°的直線l與拋物線分別交于點M1,M2，若|AM1|,|M1M2|,|AM2|成等比數列，則實數p的值為

( )

A.1 B.4

C.1或4 D.非上述答案

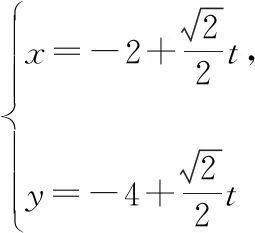
點評明確參數t的幾何意義，并與二次方程根與系數的關系有機結合，便可使本題巧妙獲解，增加了思維量，減少了計算量.

5.求參數的范圍

例5.若拋物線y=ax2-1上始終存在關于直線x+y=0對稱的兩點A,B，則實數a的取值范圍是

( )

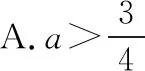
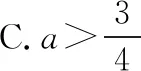
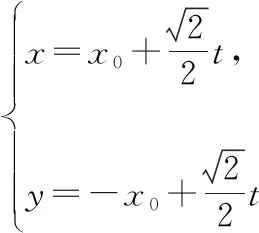
點評本題的解法有很多種，但巧設直線AB的參數方程，再借助參數t的幾何意義和根與系數的關系可獨辟蹊徑，解題過程令人耳目一新.

6.求分點的坐標

例6.已知經過點P(2,9)，斜率為2的直線l與圓x2+y2=50交于A,B兩點，則線段AB的一個三等分點M的坐標為

( )

A.(-1,3)

B.(-3,-1)

C.(-1,3)或(-3,-1)

D.非上述答案

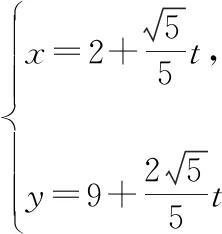
點評寫出直線l的參數方程并通過解方程求出A,B兩點對應的參數t1,t2，進而可求得三等分點M對應的參數t0，在求t0時類比了定比分點公式，充分體現出參數t作為“線坐標”的幾何意義.

7.求中點的軌跡

例7.過點C(2,1)作直線l交雙曲線x2-y2=1于A,B兩點，則弦AB中點M的軌跡方程為

( )

A.y2-x2+2x+y=0 B.y2-x2-2x+y=0

C.x2-y2+2x+y=0 D.x2-y2-2x+y=0

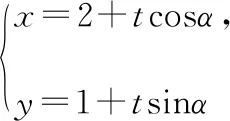
點評寫出直線AB的參數方程，則中點M對應的參數t0便可由參數α來表示，而消去α是解本題的難點和關鍵.同時，保持運算的等價性對數學素養提出了較高的要求.

8.求面積的最值

( )

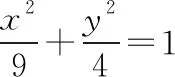
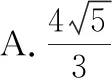
C.3 D.非上述答案