一道浙江立體幾何高考試題的探究與教學啟示

浙江 李安毓

2019年是浙江新高考改革后文理合卷的第三年，整套試卷在對文理合卷后的數學高考要求與特點維持穩定的基礎上，體現了穩中有進的命題思路.今年高考結束后，筆者接到通知，有幸參加了浙江高考網上評卷工作.通過本次高考閱卷，使筆者對考生的答題情況、得分情況，以及學生學習與教師教學中存在的問題有了全面的了解和掌握.現與廣大同仁分享本次閱卷的經歷和感悟，以期能有力地指導高三復習教學，從而提升高考復習時效.下面就以2019年浙江高考第19題為例，談談該題的試題剖析、解法探究以及今后浙江數學高考立體幾何題型的備考策略.

1.試題賞析

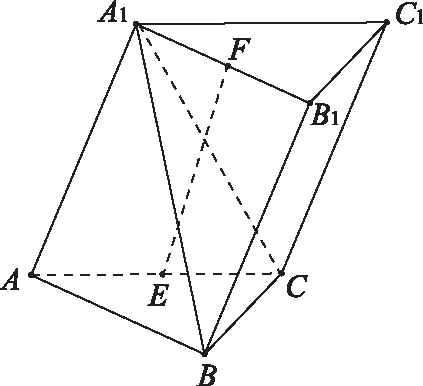
【原題】如圖，已知三棱柱ABC-A1B1C1，平面A1ACC1⊥平面ABC，∠ABC=90°，∠BAC=30°,A1A=A1C=AC，E,F分別是AC,A1B1的中點.

(Ⅰ)證明：EF⊥BC；

(Ⅱ)求直線EF與平面A1BC所成角的余弦值.

2.試題剖析

該試題以三棱柱為載體，考查空間點、線、面位置關系中的線面垂直的判定、直線與平面所成角等立體幾何模塊中的核心知識點.同時檢測考生直觀想象、邏輯推理與數學運算等數學核心素養.它作為高考數學中的第二道解答題，相對而言屬于大部分學生都容易拿分的中檔題.試題緊扣教材，語言簡練注重“雙基”，起點低入口寬，具有明顯的“浙江風格”.與2018年高考浙江卷立體幾何大題相比，熟悉的背景、相似的問題、常規的方法，命題風格可謂一脈相承.相信很多考生對兩小題的設問方式倍感“親切”，無非是把去年19題中的組合體改為斜三棱柱，把第(Ⅰ)問中的證明“線面垂直”改為了“線線垂直”，第(Ⅱ)問仍是 “線面角問題”，只是改為 “求線面角余弦值”.總之，浙江立體幾何大題繼承了近幾年來的浙江傳統和特色，整體趨于平穩，屬于意料之中的題型.特別是第19題第(Ⅱ)問,文理合卷后連續三年考查了“線面角”問題，同時此問題的求解也凸顯了多種通性通法，如幾何法、空間向量法(坐標法)和等體積法.就難度而言，2018年立體幾何題的去零平均分為11分左右，難度系數為0.73，2019年此題的去零平均分為10.6分，難度系數為0.7，相比之下兩年試題難度基本持平.

3.解法探究及考生答題情況分析

本著公平公正的原則，負責本題的評卷小組長們經過認真研討、嚴密論證，再三商榷后確定了幾種不同的解題方案與相應的評分標準.并把兩小問的分值分配為第(Ⅰ)問6分、第(Ⅱ)問9分，滿分15分.

3.1 第(Ⅰ)問證法探究

每年的浙江數學高考試題都普遍具有豐富的背景和內涵，其立意深遠、入口通道眾多，從不同的視角切入，同樣的精彩紛呈，而每一種解題思路的背后無不閃耀著數學思想的光輝.以下筆者分別給出2019高考浙江卷第19題兩小問的幾種不同視角的解法.

證法1(線面垂直法)：連接A1E，因為AA1=A1C,E為AC中點，所以A1E⊥AC.又平面A1ACC1⊥平面ABC且交線為AC，故A1E⊥平面ABC,所以A1E⊥BC.又由題知AB⊥BC且AB∥A1F,故BC⊥A1F，因此BC⊥平面A1EF,從而EF⊥BC.

評注：此證法主要運用線面垂直的判定定理來證線線垂直，屬于較為常規的通性通法.考生雖容易下手，但從閱卷的情況來看，在證明A1E⊥平面ABC的過程中，相當一部分考生只得到了一個線線垂直就推導出線面垂直，屬于判定定理知識掌握不到位而導致的錯誤，故而只能得2分.此外，在證第一個垂直關系A1E⊥BC時，需利用面面垂直性質定理來證，但很多考生因為面面垂直性質不會用而缺少一個線線垂直條件造成失分，充分說明很多考生立體幾何基礎知識還不夠扎實，或是空間感知能力較差不能靈活把握空間圖形整體結構以至于證不出第二個垂直關系.

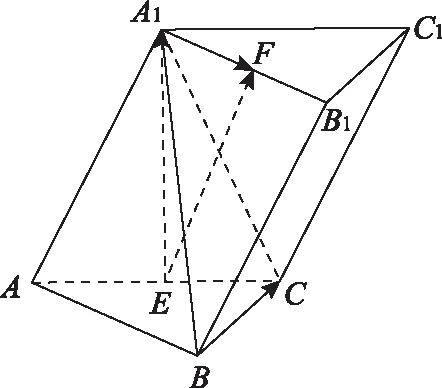
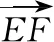
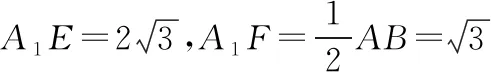
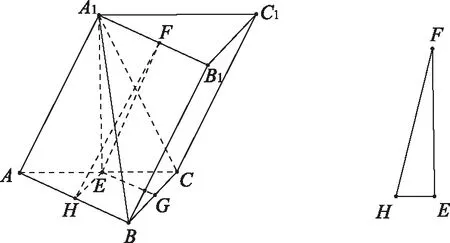
評注：此證法關鍵是利用“直接法”把BC，EF平移到同一個三角形中,再運用勾股定理來證線線垂直.從閱卷統計來看，大約有10%的考生采用此方法.雖然不少考生能想到此思路，但大都在計算邊長時出錯或存在困難，還有部分考生只計算出兩條邊長，馬上反過來運用勾股定理求得第三邊，于是就說三邊滿足勾股定理，因此EF⊥BC.此思路明顯犯了邏輯錯誤，即在未完全計算出三邊邊長時就默認該三角形是直角三角形了，屬于邏輯推理順序顛倒，導致失分.

5)成果數據導出。將服務器中更新好的1∶250 000 DLG數據庫導出為FILE GEODATABASE格式，并按目錄組織結構整理成果數據[1]。

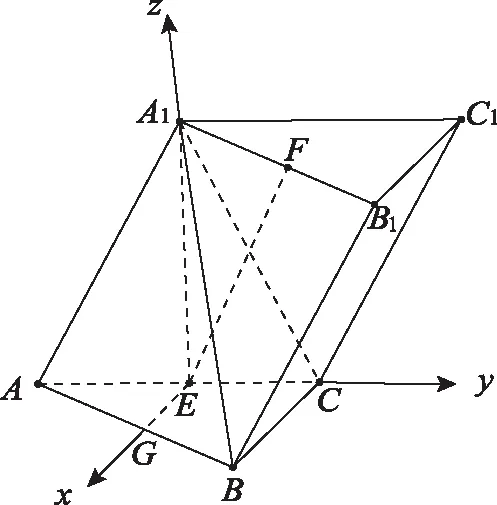
評注：該證法的關鍵是建立空間直角坐標系，利用兩空間向量的數量積為零來證得線線垂直.從評卷情況來看，兩小問凡是運用空間向量坐標法都最容易得分，但該解法對考生的數學運算能力有著較高的要求.評卷中遇到的重點問題是：在建立空間坐標系時，相當一部分考生由于審題不清，誤把斜三棱柱當成直三棱柱，并把側棱或其平行線當成z軸導致建系錯誤；還有的考生則是建系雖正確，但卻把某一個點或向量的坐標算錯，從而造成失分.

3.2 第(Ⅱ)問解法探究

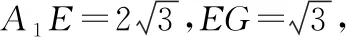
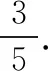
評注：數學概念是數學學科之本，也是一切數學原理規律、定理性質之源.幾何法思路的關鍵就是運用“線面角”的概念作垂線得射影從而得到線面角，進而運用余弦定理求得線面角的余弦值.由于此解法需要考生具備扎實的幾何功底，如靈活添加多條輔助線，通常大部分學生都比較畏懼，所以采用幾何法的考生只有極少部分.但凡是用了此法的幾何功底過硬的考生，基本都能算對.另外，從浙江高考命題規律來看，第一問的結論往往是為第二問服務的，本題也不例外.事實上，第(Ⅰ)問證明的EF⊥BC是為第(Ⅱ)問求線面角做鋪墊、埋伏筆的，因此試題也體現了命題人在命制解答題時對兩小問層層遞進的設計思路.然而很多考生卻忽略了第一小問的作用和價值，未能很好地利用第一問去解決第二問.究其原因是考生對面面垂直的性質以及線面角概念的理解和運用不夠熟練和靈活，故而暴露出這兩個立體幾何的核心知識點是許多考生高考復習盲區的問題.

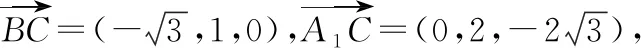
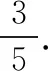
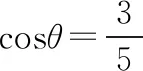
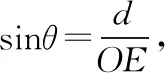
4.教學啟示及備考策略

4.1注重答題策略的培養

在平時的高三復習教學中，尤其應重視對學生解答題的答題策略進行針對性地指導和點撥，比如讓學生明白正規考試(包括模考、高考)中，解答題的首要評卷原則是分步驟采點評分，即寫對一個得分點步驟，就能得到相應的分數.縱觀近幾年的浙江高考，命題者與評卷小組越來越關注考生數學思維過程的展現，只要考生正確理解相關概念、公式定理，推理嚴密、計算準確，無論用哪一種方法都是等值的，都能得到相應的分數.同時，在高考立體幾何復習中應對學生特別強調，在答題過程中重視證明語言表達的邏輯性與規范性，語言連貫、思路清晰很重要.因為字跡清楚、卷面整潔、解題思路清晰、推理過程簡潔，閱卷教師更容易區分和辨別得分點，考生也就越容易獲得盡可能多的分數.

4.2重視邏輯推理能力的培養

立體幾何試題本身對邏輯推理能力有著較高要求，特別是第(Ⅰ)小問的證明題需要考生具備良好的邏輯推理能力，同時還需注意語言表述的條理性與嚴謹性.然而在本次高考閱卷中，發現很多考生在第(Ⅰ)問證明“線線垂直”時，因為推理不到位、論證不嚴密而導致丟分.因此在平時高三教學中，應重視對學生邏輯推理能力的培養.同時閱卷中也注意到越是推理能力好的考生，其證明過程的書寫與表達越簡潔明了，從而也就越容易得滿分.

4.3關注數學運算能力的培養