試談一道高考題中直觀想象素養各水平的體現

湖北 周 威

《普通高中數學課程標準(2017年版)》(以下簡稱“課標”)對直觀想象核心素養的內涵和主要表現做了具體描述，并將其劃分為“三個水平”.如何理解具體試題中數學核心素養的應用與滲透？根據課標要求，在高考命題路徑中對于每道試題，除了給出傳統評分標準外，還需要給出反映相關數學學科核心素養的水平劃分依據.本文基于直觀想象素養的“水平劃分”層次，探討2019年全國卷Ⅲ理科數學21題中直觀想象素養的水平層次和表現形式.

一、直觀想象素養的內涵與水平劃分

1.直觀想象素養的內涵

課標明確提出，直觀想象是指借助幾何直觀和空間想象感知事物的形態與變化，利用空間形式特別是圖形，理解和解決數學問題的素養.主要包括：借助空間形式認識事物的位置關系、形態變化與運動規律；利用圖形描述、分析數學問題；建立形與數的聯系，構建數學問題的直觀模型，探索解決問題的思路.直觀想象是要依靠平面幾何或空間幾何的直觀描述、理解和解決問題，提升學生的數形結合能力，在具體的情境中感悟事物的本質.

2.對直觀想象素養的水平劃分與理解

各個水平的含義描述分別從情境與問題、知識與技能、思維與表達、交流與反思等方面進行了闡述.

在課標案例22“跑道問題”中，跑道由左右兩邊均是半徑為36m的半圓弧與兩條直線段組成，如果能夠計算出每條直道的長度，可以認為達到直觀想象素養水平一的要求，能夠利用直角坐標系寫出跑道(上半部分)的解析式，可以認為達到直觀想象素養水平二的要求；在案例29“估算地球周長”中，能夠通過“立竿測影”的描述畫出平面示意圖，可以認為達到直觀想象素養水平一的要求，能夠借助平行線內錯角相等的知識遷移或推理得出清晰的數與形之間的邏輯關系，進而得出地球周長，可以認為達到直觀想象素養水平二的要求.再根據案例30“影子問題”，案例31“圓柱體截面問題”，不難將“直觀想象素養水平一”理解為“數”與“形”之間的直譯；“直觀想象素養水平二”可以理解為“數”與“形”之間運用聯想、知識遷移所反映出來的聯系；“直觀想象素養水平三”可以理解為“數”與“形”之間通過知識的創新性、數學分支之間及學科之間綜合應用性所反映出來的“深層次”的聯系.

因此，從上述對各個水平的總結與理解來看，特別是水平二、水平三，由于“數”與“形”之間運用聯想角度、知識遷移的難易類別及數學知識點不同，采用的數學分支或所跨學科不同，往往存在同一情境與問題的同一直觀圖形中也會體現出不同的直觀想象水平，同一水平也有不同的“知識與技能”、“思維與表達”方面的呈現方式.

課標中提到，數學學業質量水平二是高考的要求.包含了六大核心素養水平二階段的綜合要求，其中對直觀想象的要求可概括為：能夠想象并構建相應的幾何圖形，發現圖形與圖形、圖形與數量的關系，探索圖形的運動規律；能夠掌握研究圖形與圖形、圖形與數量之間關系的基本方法，借助圖形性質探索數學規律，解決實際問題或數學問題；能夠用圖形探索解決問題的思路，形成數形結合的思想.

二、基于高考題探討直觀想象素養的各水平層次

接下來從直觀想象水平劃分的角度對2019年全國卷Ⅲ理數解析幾何題進行案例探討.解析幾何的本質是用代數的方法來研究幾何問題，所以解析幾何是“數”與“形”結合的經典內容，借助“形”的直觀來更有效地解決問題并沒有否定“用代數的方法來研究幾何問題”的本質.

(Ⅰ)證明：直線AB過定點;

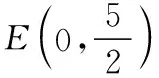
1.水平一的表現

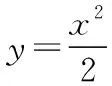
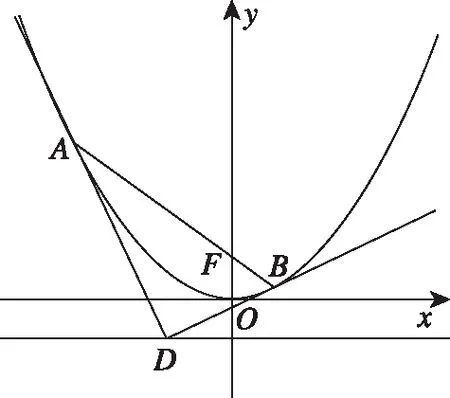
圖1

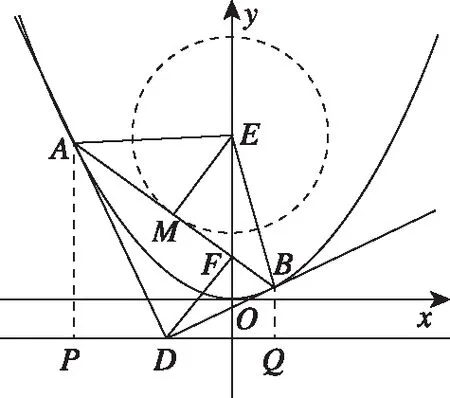
圖2

2.水平二的表現

第(Ⅰ)問中若能利用求導公式、導數與斜率的關系，聯想到切線DA,DB都過公共點D，以此求直線AB的方程，可以認為達到水平二的要求.具體回答如下：

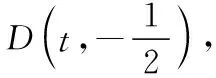
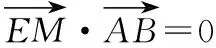
2.1 表現形式一

知識與技能:利用EM與AB的斜率，根據弦長公式|AB|及點到直線AB的距離進而求得面積.

思維與表達:從直線出發，將直線代入拋物線方程

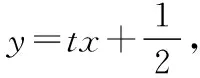
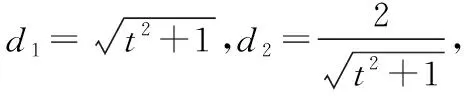
2.2 表現形式二

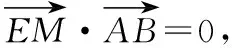
思維與表達:從點出發，利用向量與面積之間的關系

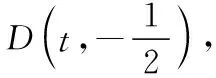
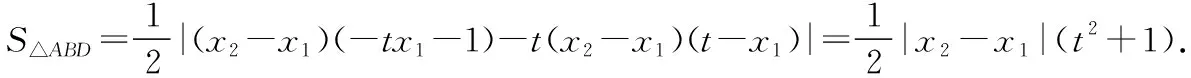
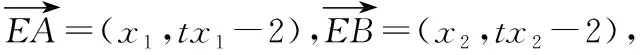
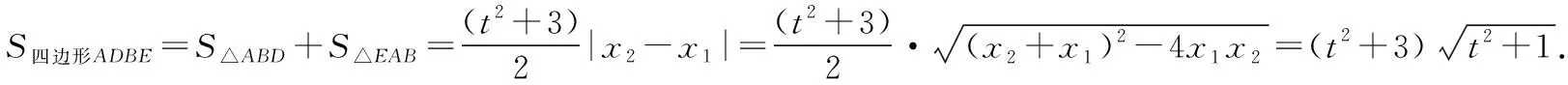
3.水平三的表現

是否可以基于以上情境與問題中的直觀圖形體現直觀想象水平三的層次呢？筆者以為，第(Ⅱ)問如果從三角函數方面的相關知識結合圖2利用參數法這個“創新”的角度得到解答，根據加分原則和滿意原則，可以認為達到“水平三”的要求.主要思維與表達如下：

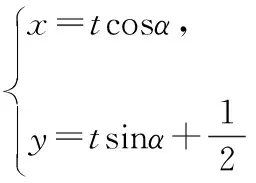
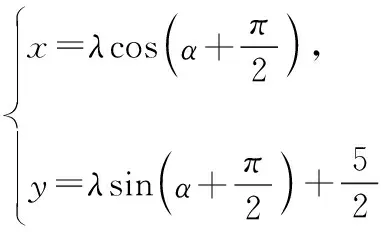
三、培養直觀想象素養的備考啟示

根據以上分析，水平一、二、三是直觀想象素養的不同層次水平，在情境與問題、知識與技能、思維與表達、交流與反思等方面有相應的劃分依據.事實上，往往存在同一情境與問題中會體現出不同的直觀想象水平，同一水平也有不同的“知識與技能”“思維與表達”方面的呈現方式，所以備考中如何利用例題進行通性通法的解題教學，通過一題多解和多題一解讓學生能解一題而通一類題，避免“會而不對、對而不全”的現象.因此，在教學備考中，首先要深刻把握各個核心素養的水平劃分的內涵；其次要創設合理的情境，針對不同核心素養的不同水平設置問題；再次要利用好成熟的“直觀模型”，例如幾類特殊圓錐曲線圖形模型、函數圖形模型等；最后就是突出數形結合思想.