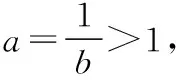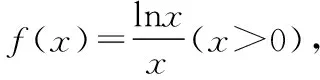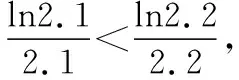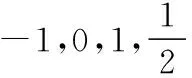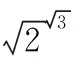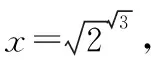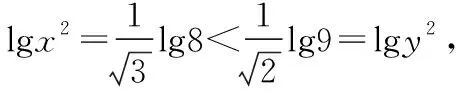心有“0”犀“1”點通
——淺議指對冪比較大小的常用技巧

四川 杜海洋

(作者單位:四川省成都經濟技術開發區實驗中學校)

從近幾年高考情況來看，指數、對數及冪的大小比較為高考的熱點內容，一般以選擇題為主.這類考試題目通常是三個指數和對數及冪混在一起，進行排序.解決這類問題如果兩兩進行比較，有時則花費的時間較多，本文介紹處理此類問題的常用方法與技巧.

涉及指對冪比較大小時，如果式子中易求大于0或小于0先區分還容易辦到，但讓學生感到困難的是當式子的值都大于1或小于1時，此時的技巧手段就需要有高招了，即0，1是這類問題的分水嶺，下面筆者以一些典型例題來說明此類問題的方法與技巧，以饗讀者！

一、比較大小的基本思路

(1)求同存異:如果兩個指數(或對數)的底數相同，則可通過指數(真數)的大小與指數(或對數)函數的單調性判斷出指數(或對數)的關系，所以要熟練運用公式，盡量將比較的對象轉化為某一部分相同的情況.

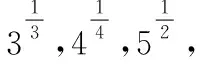
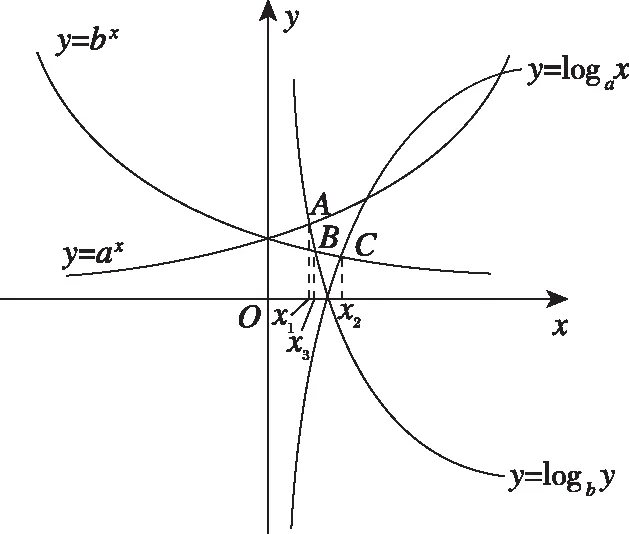
(2)利用特殊值作“中間量”:在指對數中通常可優先選擇“-1，0,1”對所比較的數進行劃分，然后再進行比較，有時可以簡化比較的步驟(在兵法上可稱為“分割包圍，各個擊破”)，也有一些題目需要選擇特殊的常數對所比較的數的值進行估計，例如log23，可知1=log22

(3)利用函數的單調性比較大小:例:f(x)在[a,b]上單調遞增，則?x1,x2∈[a,b],x1

總之，比較數式的大小，若同底，考慮指數函數(或對數函數)；若同指，則考慮冪函數，再利用函數的單調性比較大小；若不同底，也不同指，則其基本方法是“同底法”，即把不同底的對數式化為同底的對數式，然后根據單調性來解決，或者利用中間量法.

二、比較大小的常用方法

策略一、估算法

就是把復雜問題轉化為較簡單的問題，求出答案的近似值，或把有關數值擴大或縮小，從而對運算結果確定出一個范圍或作出一個估計，進而作出判斷的方法.

【例1】比較log39.1與log23.9的大小.

【解析】因為1=log22log23.9.

策略二、特殊值法

就是運用滿足題設條件的某些特殊數值對各選擇支進行檢驗或推理，利用問題在某一特殊情況下不真，則它在一般情況下也不真的原理，由此判斷選項真偽的方法.用特例法解選擇題時，特例取的越簡單、越特殊越好.

【例2】若a>b>1,0

( )

A.ac

C.alogbc

【針對訓練2】若非零實數a,b滿足2a=3b，則下列式子一定正確的是

( )

A.b>aB.b

C.|b|<|a| D.|b|>|a|

【解析】令a=2,則4=3b，易得1b.

策略三、數形結合法

就是利用函數圖象或數學結果的幾何意義，將比較大小與某些函數圖象結合起來，利用函數圖象性質，再輔以簡單計算，確定正確答案的方法.

( )

A.a>b>cB.b>a>c

C.a>c>bD.c>a>b

在同一平面直角坐標系中分別作出函數y=log2x,y=log3x,y=log4x的圖象,如圖所示:

( )

A.x3

C.x1

策略四、單調性比較法

解題時根據實際情況來構造相應的函數，利用函數單調性進行比較大小，如果指數相同，而底數不同則構造冪函數，若底數相同而指數不同則構造指數函數.然后根據函數的單調性進行比較大小.

【例4】已知a=2.12.2,b=2.22.1,c=log2.22.1，則

( )

A.c

C.a

所以c

( )

A.x>y>zB.z>y>x

C.y>x>zD.z>x>y

策略五、中間量法

【例5】

類型1、指數型(橋梁a0=b0=1)

(1)比較大小1.70.3________0.93.1.

【解析】觀察題目可發現兩個數的底數、指數都不同，但可以根據指數函數的單調性，構造中間量，與數1先進行比較.知1.70.3>1.70=1=0.90>0.93.1.

注意:在研究指數函數時，總會提到a0=1(a>0,a≠1)，即指數函數過定點(0,1)，更深入一些理解，這個定點也是一個重要的分界點，把函數值分為了大于1和小于1兩部分.

【解析】底數、指數都不同，構造中間量比較大小，先與數1，0比較.

(3)已知a=log20.2，b=20.2，c=0.20.3，則

( )

A.a

C.c

【解析】a=log20.220=1，∵0<0.20.3<0.20=1，∴c=0.20.3∈(0,1)，∴a

類型2、對數型(0=loga1=logb1)，(1=logaa=logbb)

( )

A.a>b>cB.a>c>b

C.c>a>bD.c>b>a

(2)設a=log54，b=(log53)2，c=log45，則

( )

A.a

C.a

【解析】∵a=log54log44=1，

∴c最大，又因為a,b∈(0,1)，但b=(log53)b，故選D.

【點評】本題考查指數的運算性質和對數的運算性質，在涉及比較兩個數的大小關系時，有時借助于0,1這樣的特殊值能起到事半功倍的效果.

類型3、以上講的兩種類型，都是用比較常見的0,1作為橋梁進行大小比較，然而有些值不能用0,1來作為中間量進行比較，但是我們仍然能夠找到其他的中間量.

兩者均大于1或均小于1且大于0

(1)0.80.5________0.90.4.

【解析】由式子可得兩者均小于1，這時我們可以構造中間量0.90.5或0.80.4，目的是轉化與其中一個式子構造同底，與另一個式子構成同指，即比較sm，tn的大小，構造中間量sn或tm.0.80.5<0.90.5<0.90.4.

(2)log3.12________log32.1.

(3)已知a=log910，b=log1011，比較a,b的大小.

【針對訓練5】試比較log54與log43的大小.

即:比較logab，logmn的大小，構造中間量logan或logmb.

策略六、對數法比較大小

上面的題目可以用函數方法或中間量的方法來比較大小，但是有些題目，靠上述手段很難比較大小，我們就需要新的武器——對數法比大小.我們看下面的題目，這時就顯示出對數法比大小的優勢.

注意:此時中間量并不能判斷出兩數大小，所以我們轉換思路，用取對數的方法，進行比較.

【針對訓練6】若a>0,b>0,比較algb與blga的大小.

【點評】1.對數法比大小，先取對數，比較對數值的大小，得到真數的大小；2.只適用于比較兩個正數的大小，遇到負數需要先做出轉化.

指數、對數及冪的大小比較問題方法靈活，常常給人以“亂花漸欲迷人眼”的感覺，而對其問題進行歸納總結，會發現這類問題的解法往往可以從代數和幾何兩個方面加以探尋，即利用函數的性質及圖象解答，體現對數學抽象、邏輯推理、數學建模、數學運算及直觀想象等核心素養的考查.當然除了以上介紹的方法外還有作商、作差等比較大小的方法，有時一題也可從不同的方法入手均可獲得突破，以上舉例起到一個拋磚引玉的作用，平時在學習時多留意，多積累，相信以后解決此類問題時就會有“淺草才能沒馬蹄”的輕盈之感.