液體粘滯阻尼器減震結構功率譜密度分析方法

陳夏楠， 張令心， 陳永祁， 朱柏潔

(1．中國地震局工程力學研究所 中國地震局地震工程與工程振動重點實驗室，黑龍江 哈爾濱 150080；2．北京奇太振控科技發展有限公司，北京 100037)

近年來，消能減震技術在結構抗震中的應用日益廣泛。消能減震結構的地震反應分析方法目前主要有2種，其中最常用的一種方法是時程分析法[1-3]，但該方法計算量較大，計算結果易受地震動時程選取的影響；另一種方法是計算量相對較小的振型分解反應譜法，對于該方法，目前常用的結構有限元軟件可以將阻尼元件附加給結構的阻尼轉換成為振型阻尼比進行計算，但上述對附加阻尼的處理方法使得結構分析過程不能考慮模態耦合的完全阻尼[4]。功率譜密度分析方法采用地震動的功率譜密度函數作為地震激勵，而功率譜密度函數包含了隨機地震荷載的統計特征，因此可以彌補上述方法的不足。虛擬激勵法[5-6]是功率譜密度分析方法在土木工程領域運用較多的方法，但由于物理概念相對復雜，該方法在實際工程結構的減震計算分析中應用較少。針對以上問題，本文提出一種基于功率譜密度函數的附加液體粘滯阻尼器結構地震反應分析方法，并進一步結合結構最大地震反應的概率估計方法提出了該類型結構的地震可靠度分析方法，且該方法可通過實際工程結構分析中廣泛使用的通用有限元軟件SAP2000得以實現。利用算例對比該方法與時程分析法、振型分解反應譜法的計算結果，并采用該方法進行附加液體粘滯阻尼器結構的地震可靠度分析。

1 基于功率譜密度附加液體粘滯阻尼器結構地震反應及可靠度分析方法

功率譜密度函數可以完整反映規范設計反應譜的統計特征，相比隨機抽樣得到的地震動時程曲線，它在統計意義上與規范設計反應譜更為接近。本文根據《建筑抗震設計規范》[7]中的設計反應譜求出相應的功率譜密度函數曲線，并確定了結構的阻尼，估算出結構在地震作用下最大反應的概率，并采用結構有限元分析軟件SAP2000實現了附加液體粘滯阻尼器結構的地震反應及可靠度分析。

1.1 功率譜密度分析方法及參數選取

1.1.1 功率譜密度分析方法概述

本節通過時域分析與頻域分析之間的轉化關系，介紹結構頻域內分析的運動方程以及功率譜密度分析的過程。假定x(t)為結構的位移時程函數，xg(t)為地面位移時程函數，在時域內，結構地震反應為[4]：

(1)

式中：M、C、K分別為結構質量矩陣、阻尼矩陣和剛度矩陣；Ceq為液體粘滯阻尼器等效線性阻尼系數矩陣。其中：

(2)

式(2)即為頻域內結構地震反應的運動方程。

在SAP2000中，當使用功率譜密度分析方法時，運動方程右側采用的輸入荷載形式為[4]：

(3)

經過功率譜密度分析，可以得到結構對應不同頻率點的地震反應。

1.1.2 功率譜密度函數的選取

由于目前振型分解反應譜法為主流的結構設計方法，因此，求出對應規范[7]設計反應譜的功率譜密度函數對結構設計十分重要。擬合功率譜密度函數的方法主要有2種：一種為迭代法[8-11]，另一種是用概率的方法推導出地面加速度功率譜與結構最大加速度反應譜之間的近似關系[12]。

對于迭代的方法，在迭代出一組滿足誤差要求的譜值之后，通常會用最小二乘法將其擬合為金井清譜的譜參數，即將數據擬合為過濾白噪聲模型來模擬地震動的功率譜密度分布[13]。本文采用了文獻[13]選用柱修力-陳厚群功率譜的修正過濾白噪聲模型，所選用的功率譜密度函數為：

(4)

式中：D、ω0、ξg、S0分別代表高頻拐角周期、低頻拐角頻率、場地特征周期和譜強度。

1.1.3 阻尼的定義

結構的阻尼通常來源于2部分，一部分是作為整體應用到整個結構的阻尼，為方便計算，它常被分解為剛度比例阻尼和質量比例阻尼；另一部分為附加阻尼元件的阻尼。在時域內阻尼力F為：

(5)

式中：C為阻尼系數；α為速度指數；v(t)為相對速度。而在頻域內，由于SAP2000不能進行速度非線性的分析，因此需要首先根據耗能相等的原則，計算出等效線性阻尼。在SAP2000中，對于線性阻尼，程序可自動指定頻域內滯回阻尼D(ω)為ωC[4]。

1.2 結構地震作用下最大反應的概率估計

功率譜密度函數描述了隨機振動在頻域內的統計特征，而結構反應在時域內達到某個特定值的概率是與功率譜密度函數在頻域內的統計特征緊密相關的。因此，根據功率譜密度分析得到的結構反應的譜密度函數，可以求出該反應的均方根等統計參數，利用這些統計參數可以估算出結構反應的概率。達文波特[8]給出了隨機振動中，結構反應y的絕對值在(0，Td)時段內不超過a的概率：

(6)

式中：

r=a/σy

(7)

(8)

(9)

1.3 基于功率譜密度的附加液體粘滯阻尼器結構地震反應及可靠度分析在SAP2000中的實現

采用SAP2000進行附加液體粘滯阻尼器結構地震反應及可靠度分析的主要流程為：

1)建立結構有限元模型；

2)定義線性粘滯阻尼器及其參數；

3)定義功率譜密度函數及功率譜密度分析工況；

4)運行分析，保存結果，主要結果包括結構及阻尼器地震反應的頻率-譜強度曲線，以及反應均值；

5)根據1.2節的公式計算結構及阻尼器的地震反應不超過某一特定值的概率。

2 三種結構地震反應計算方法對比

本文對附加液體粘滯阻尼器的結構分別采用振型分解反應譜法、功率譜密度分析法以及線性時程分析法計算其地震反應，對3種方法的計算結果進行對比。

2.1 結構有限元模型

選取一棟13層框架-剪力墻結構，結構平面圖如圖1(a)所示；結構平面柱距6 m，層高3.2 m，墻、柱混凝土強度等級為C40，梁板混凝土強度等級為C30，柱截面700 mm×700 mm，梁截面300 mm×600 mm，樓板厚120 mm，剪力墻厚200 mm，樓板所加恒載和活載均為3 kN/m2。利用SAP2000建立該結構的有限元模型，見圖1(b)。模型中框架梁、柱采用桿單元；剪力墻采用薄殼單元；樓板采用膜單元，只起到傳導豎向荷載的作用。

圖1 算例1有限元模型Fig.1 Finite element model of example 1

為了對比3種方法對于阻尼器減震效果的計算結果，本文設計了3個結構模型，分別為無阻尼器結構、有阻尼器且阻尼系數C為1 000 kN/(m·s-1)的結構(以下簡稱附加阻尼器結構1)、有阻尼器且阻尼系數C為3 000 kN/(m·s-1)的結構(以下簡稱附加阻尼器結構2。阻尼器僅沿Y向布置，布置在結構剪力墻的2側，與剪力墻在一條直線上，每層4個，隔層布置，共布置24個。定義結構自身阻尼比為0.05。

2.2 地震荷載

結構所在場地位于我國東部地區，抗震設防烈度Ⅷ度(0.2g)，場地類別為Ⅱ類，地震分組為第一組，根據文獻[13]，式(4)中的高頻拐角周期D與地震震級有關，首先根據設防烈度和地震分組，查表得到該場地震級相關參數M為6.26，再根據文獻[14]表6地震震級與D值的關系，用插值法求高頻拐角周期D為：

D=0.01492

(10)

低頻拐角頻率ω0為：

ω0=2πβ/3r=2π×3.5/(3×4)=1.832 59

(11)

杜修力等[15]指出可忽略震級對等效圓盤半徑r的影響，直接將r取為4 km，由此計算得到ω0的值，如式(11)所示。最后根據文獻[13]總結得出的不同設防烈度、場地類別以及地震分組所對應的場地土阻尼比ξg、卓越角頻率ξg以及譜強度因子S0分別為0.726、18.05、58.99。

將以上各參數代入式(4)，得到場地地面加速度的功率譜密度函數曲線如圖2所示。

圖2 地面加速度功率譜密度函數曲線Fig.2 PSD function curve of the ground acceleration

2.3 計算結果分析

對每組結構分別采用振型分解反應譜法、功率

譜密度分析法和直接積分的線性時程分析法進行Ⅷ度小震作用下的計算分析，其中線性時程分析所采用的地震動為根據《建筑抗震設計規范》[7]中的設計反應譜生成的10條人造地震動。人造地震動的反應譜與規范反應譜見圖3。結構基底剪力的計算結果如表1所示。

圖3 規范反應譜與人造地震動反應譜Fig.3 Response spectrum curves of design ground motion and artificial ground motion

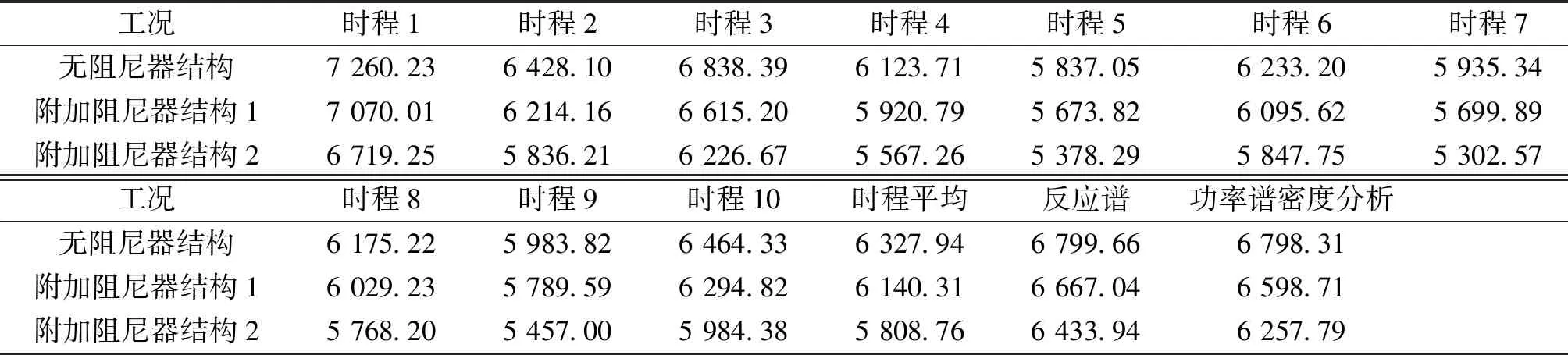
表1 3個結構的基底剪力計算結果Table 1 Base shear of 3 structures kN

直接積分的線性時程分析因適用性較廣，在附加液體粘滯阻尼器結構的地震反應分析中，其結果常被作為對比驗證值。采用振型分解反應譜法和功率譜密度分析法得到的計算結果與線性時程分析法得到的平均值的誤差對比，見表2。其中誤差的計算方式為振型分解反應譜或功率譜密度分析計算結果與時程分析計算結果差的絕對值除以時程分析計算結果。從表中可以看出，功率譜密度分析法與時程分析法的計算結果更為接近。

表2 振型分解反應譜法與功率譜密度分析法較時程分析法誤差對比

表3為不同方法計算的各模型附加阻尼器后基底剪力減小的百分比，從表中可以看出，功率譜密度分析與直接積分的線性時程分析結果更加接近。

表3 結構基底剪力減小百分比Table 3 Decrease percentage of structural base shear %

通過上述結果對比可以看出，功率譜密度分析法計算的精度可以滿足工程需要，該方法適用于附加液體粘滯阻尼器結構的地震反應分析。

3 基于功率譜密度的結構地震反應及可靠度分析方法應用算例

本節以實際工程結構模型作為分析對象，對使用非線性液體粘滯阻尼器減震前后的結構地震可靠度進行計算分析。

3.1 模型簡介

該結構為位于新疆地區的23層框架-剪力墻結構，結構主體地下2層，地上23層，地下2～地上4層，層高4.5 m，平面尺寸30 m×55 m，其余各層層高3 m，平面尺寸30 m×35 m，結構主體總高75 m。標準層結構平面圖見圖4(a)。該工程所在場地抗震設防烈度為Ⅷ度(0.3 g)，場地類別為Ⅱ類，地震分組為第3組。

圖4 算例2有限元模型Fig.4 Finite element model of example 2

根據前文方法選取對應場地的設計地震動功率譜密度函數曲線，如圖5所示。

圖5 地面加速度功率譜密度函數曲線Fig.5 PSD function curve of the ground acceleration

用SAP2000建立2個結構模型，一個不采取任何減震措施，另一個分別在11、13、15、21、23層設置每層4套X向阻尼器，8層設置2套X向阻尼器，8、10、12、14、16、18、22、24層設置每層4套Y向阻尼器，3層設置2套Y向阻尼器，阻尼器的安裝采用套索的形式，阻尼系數CN=1 400 kN/(m·s-1)0.3，速度指數α為0.3，由于頻域內的分析不能考慮速度非線性，因此需要根據阻尼耗能相等的原則計算阻尼器的等效線性阻尼系數[16]。

線性阻尼器和非線性阻尼器帶給結構的附加阻尼比分別為：

(12)

(13)

式中：Te結構基本周期，本例中Te=2.03 s；m為結構質量；d為阻尼器最大變形，本文取結構層間位移角達到 《建筑抗震設計規范》[7]規定上限時的阻尼器變形，d=0.00 735 m；η為計算的中間參數，由下式計算得到：

(14)

令βv1=βv2，則：

(15)

則等效線性阻尼系數為：

(16)

將各個參數值代入式(19)，計算得到Ceq=23 144.2 kN/(m·s-1)，在SAP2000中將該值定義為阻尼器的線性阻尼系數。

3.2 計算結果分析

對該結構進行功率譜密度分析，選擇層間位移角最大的層(18層)，分別輸出2對比分析結構在該層的層間位移譜強度與頻率的關系曲線，如圖6所示。

圖6 最大層間位移譜強度與頻率關系曲線Fig.6 The relation curve of maximum interlayer displacement’s spectrum intensity and the frequency

用1.2節的公式計算第18層層間位移角不超過3.75 mm(根據《建筑抗震設計規范》[7]規定的框剪結構小震下彈性層間位移角限值計算得到)的可靠度，計算結果及中間參數如表4所示。

由表4可以看出，附加液體粘滯阻尼器減震結構層間位移不超過3.75 mm的概率，即結構地震可靠度，由原結構的42.78%提高到48.81%。

表4 可靠度計算中間參數及結果Table 4 Intermediate parameters and results of reliability calculation

阻尼器變形超過極限變形作為結構失效的判斷標準，重新計算結構地震可靠度。選取變形最大的一套阻尼器，輸出其軸向變形譜強度與頻率關系曲線，如圖7所示。

圖7 阻尼器最大變形譜強度與頻率關系曲線Fig.7 The relation curve of the damper maximum deformation’s spectrum intensity and the frequency

采用式(6)～(9)進行計算，其中λ1的值為251.745，計算阻尼器變形不超過75 mm(由阻尼器生產廠家給出)的概率為100%。

將表4中P1和表5中P2對比，取小值，得到結構最終的地震可靠度為48.81%，可以看出，以結構層間位移角超限作為失效標準起控制作用。

4 結論

1)對于附加液體粘滯阻尼器結構減震效果的計算，采用基于功率譜密度分析的方法與時程分析方法的計算結果更為相似。基于功率譜密度分析方法的計算量較時程分析法小，同時該方法相較于振型分解反應譜法可以更真實的反映出阻尼器對結構的影響，因此該方法更適合于附加液體粘滯阻尼器結構的地震反應分析。

2)基于功率譜密度分析的地震反應分析方法可計算得到結構地震反應的譜強度。頻率曲線可直接應用于結構地震可靠度的計算，因此該方法也可應用于基于性能的結構設計和工程地震風險保險領域。

3)基于功率譜密度分析的結構反應分析方法可擴展至統計規律更加明顯的結構風響應的計算。