利用液晶波片去除零級像的數字全息成像研究

宋潔睿， 孫 蕾， 吳 玥， 袁子怡， 董 昊， 孔 勇

（上海工程技術大學 電子電氣學院， 上海201620）

0 引 言

數字全息技術（DH），是一種既能記錄振幅圖像又能記錄相位圖像的方式，可對物體圖像目標進行實時三維檢測和測量［1］。 此外，即使樣品焦點不在最佳位置，或者光學系統包含像差，DH 也能夠重建目標波的振幅和相位［2-3］。 基于這些優點，DH 在工業和科學領域得到廣泛的應用，特別是在生物醫學領域，實時監測活細胞的振幅和相位圖像［4］。 在工業產品制造中，通過對產品進行地形和斷層的實時檢測，可以顯著提高生產能力。

對物光和參考光干涉形成全息圖，再進行數字再現或光學再現的過程中，在成像平面中會出現零級像、原始像和共軛像。 其中零級像位于成像平面的中心，具有較高的能量，形成零級亮斑。 它會嚴重影響再現像的成像質量，導致原始像或共軛像不清晰，降低成像的信噪比，再現圖像細節較難分辨。 因此，去除再現平面中心的零級亮斑尤為重要。 目前，常用的幾種消除零級像的方法主要包括頻譜濾波［5］、空域濾波法［6-7］、相移法［8-11］等。 頻域濾波法雖能夠有效地去除零級像的干擾，提高原始像或共軛像的對比度，但普遍存在濾波窗口選擇困難且主觀性強等問題。 基于空間域的濾波方法由于計算簡單，只需記錄一幅全息圖，適于動態探測而被廣泛應用于數字全息中。 但空域均值濾波方法在濾波模板的尺寸較大時，計算速度較慢，且采用均值濾波時物體的細節變得模糊；空域有限脈沖響應濾波器在有限脈沖響應濾波后，會減弱再現像的強度。 利用相移的方式也可以很好的去除直流和共軛分量，但PZT 和波片相移全息系統具有結構復雜，響應速度較慢等缺點，而液晶空間調制器相移全息系統成本較高。 近期有人提出，采用循環迭代算法［12］和非線性濾波［13-14］等方法來消除零級衍射分量的影響，取得了較好的效果。 但迭代算法需要較長的運算時間，并且結果受初始條件影響。 非線性濾波方法僅局限于1／4 象限頻譜區域內使用，而且需要在傅里葉頻譜區域設置濾波窗口。

基于上述研究，本文提出利用電控液晶波片，在參考光路中引入任意相移δ 記錄兩次全息圖，來實現提取離軸DH 中的物體信息。 一次任意相移法可有效的消除零級項的干擾，不需要零級項和物體信息完全分離也可以實現物體信息的再現。 此系統操作簡易，只需通過控制電壓使得液晶波片產生一次任意相移，不需要其他的硬件操作和精確的相移控制，穩定性較高。 此外，還具有成本低、響應速度快、結構簡單等優點。

1 實驗原理

1.1 一次任意相移法原理

離軸數字全息記錄光學系統如圖1 所示。 其中，O 和R 分別是物光及參考光，T 是電控液晶波片，P 是是生成參考光的棱鏡，平面H 是全息記錄面。

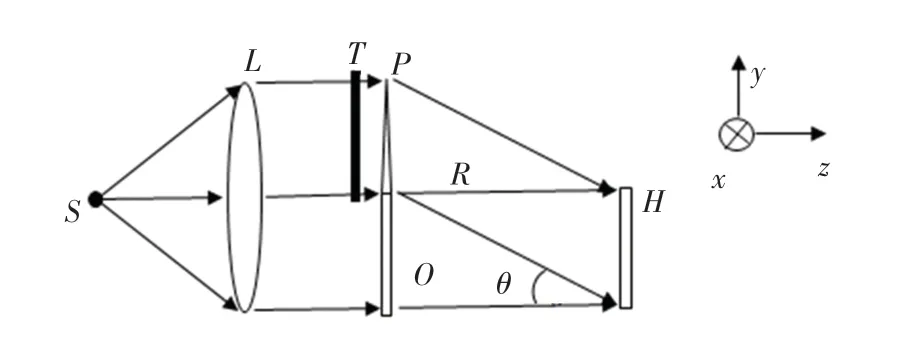
圖1 離軸數字全息光學系統Fig. 1 Off-axis digital holographic optical system

再全息面上的參考光波可表示為：

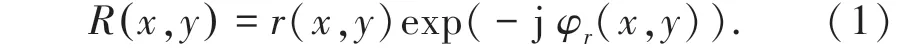
其中，r（x，y） 和φr（x，y） 分別為參考光光波的振幅和相位分布。 同理，全息面的物光波可表示為：

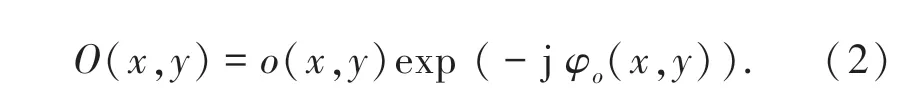
其中，o（x，y） 和φo（x，y） 分別為物光光波的振幅和相位分布。 則這兩個波在全息面上的疊加復振幅是：

該光強用CMOS 相機記錄下來，輸入到計算機得到數字全息圖：

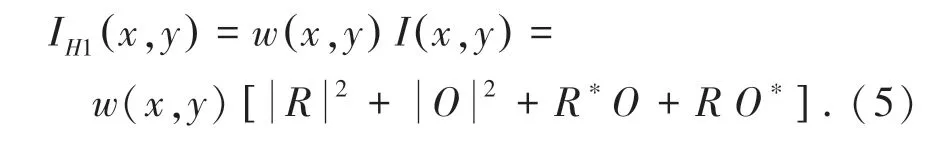
其中，w（x，y） 是CMOS 光電轉換的窗口函數。對全息圖進行再現后，前兩項的直透光和暈輪光形成的零級像；第三項含有物體信息，形成原始像；第四項攜帶物體共軛信息，形成共軛像。 重建的圖像中零級像和共軛像將對物體的原始像產生干擾，若在參考光路中加入電控液晶波片T，引入一相移δ 再次記錄一幅全息圖，即將參考光變為：

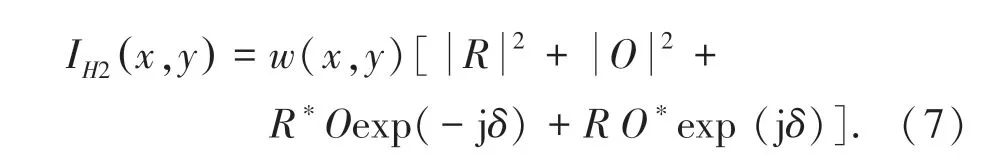
將兩次記錄的全息圖相減可以得到不含零級項的全息圖：

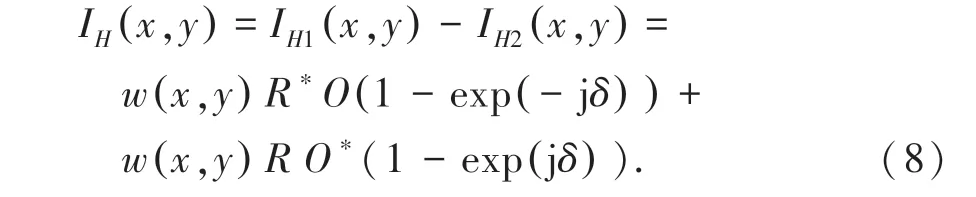
再次對全息圖進行再現后，可以得到不含零級像的再現像。

1.2 電控液晶移相原理

液晶分子結構是非對稱的，具有各向異形，通過控制液晶上的o 光及e 光折射率可以實現相位調制。

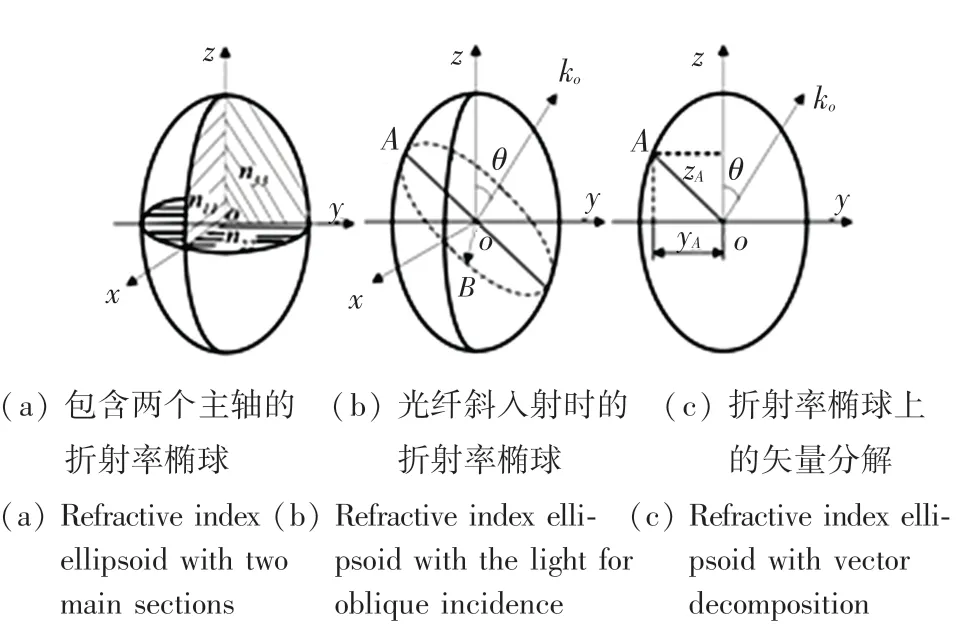
圖2 向列型液晶折射率橢球Fig. 2 Ellipsoid of refractive index of nematic liquid crystal

如圖2 所示，光線沿k0方向傳播并與z 軸成θ角，通過原點作以k0為法線方向的平面， 得到一個與橢球相截后的橢圓。 OA 和OB 是橢圓兩個主軸，兩個主軸方向也被k0所允許存在的線偏振光矢量D方向。 OA 和OB 的矢徑長度分別為這兩個方向線偏振光的折射率。 因OB 方向永遠保持和z 軸垂直，其矢徑長度恒定為n⊥，而且不隨θ 角變化而改變。 因此，沿OB 方向的光確定為尋常光o 光。 然而，OA 矢徑長度在zoy 面內隨θ 角變化而改變，沿OA 方向的光確定為非尋常光e 光。 要確定e 光的折射率，必須確定OA 矢徑長度。 當zoy 平面跟折射率橢球相截時，可以得到：

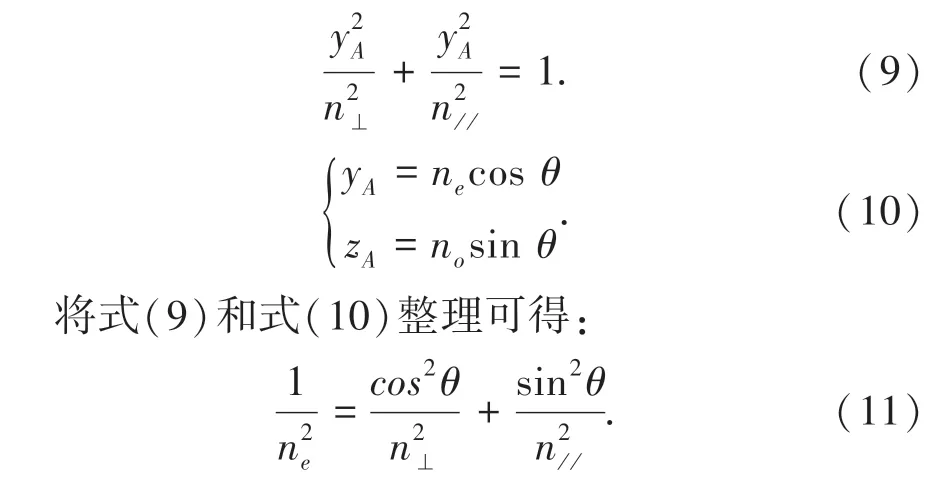
當液晶的各向異性發生雙折射后，折射率可以表示為：

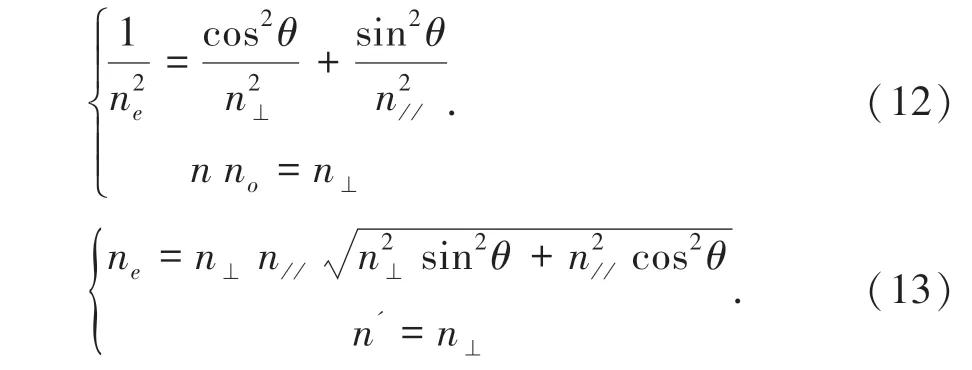
由式（13）可以分析入射向列型液晶的出射o 光和e 光的折射率。 當外界施加電壓后，液晶指向發生改變，導致液晶對e 光的折射率發生改變，使液晶的雙折射率改變，如式（14）：

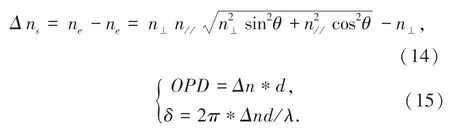
當有光射入液晶后，輸出的o 光與e 光產生光程差OPD，如式（15）。 可以得到相位延遲，通過液晶電控雙折射效應實現對光的相位調制。

液晶波片的瓊斯矩陣為［15］：

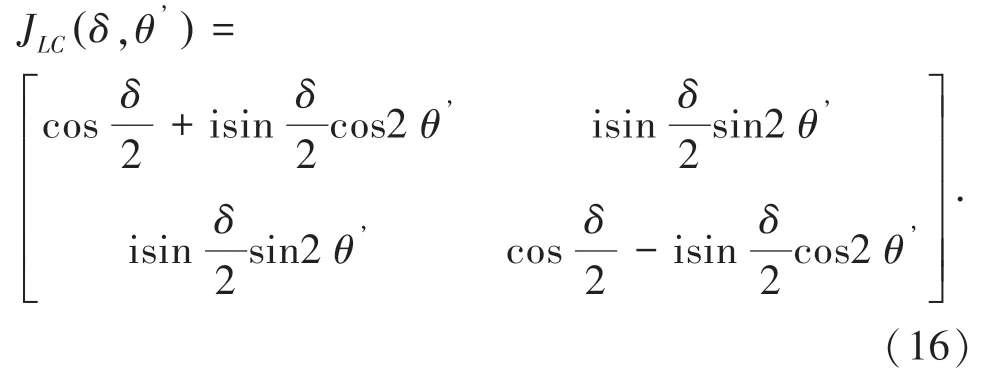
式中，θ’ 是液晶慢軸與x 軸夾角，當θ ＝90°，入射激光為平行于x 軸的線偏振光時，液晶輸出的瓊斯矩陣為［15］：

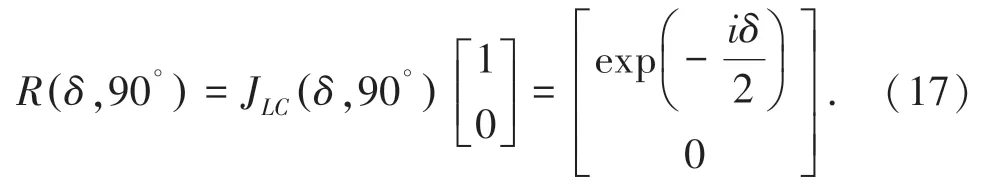
由此可見，通過調節加在液晶波片上的電壓來調節延遲。 如式（6），在參考光中引進了可調的相位，達到了移相的目的。

2 實驗結果及分析

實驗中采用離軸數字全息光路，如圖3 所示。其中，激光器輸出波長為532 nm（由長春新產業光電技術有限公司提供）；激光束經PBS 起偏后，通過分光鏡BS 分為參考光和物光兩路，參考光經過電控液晶波片T（該液晶波片為E7 向列相型，由深圳市中達瑞和科技有限公司提供）實現相移；經過濾波準直后，從反射鏡M1 反射垂直入射到CMOS 上，物光經反射鏡M2 反射照射物體，物體表面發生漫反射光與參考光在CMOS 成像面產生干涉，形成干涉全息圖；CMOS（由德國Cinogy 公司提供）記錄該全息圖并輸入到電腦中，CMOS 像素為1280×1022且每個像素大小為5.3×5.3 （μm）；拍攝實物為長寬高均為10 mm 的骰子，記錄距離為0.38 m；參考光與物光的夾角為5°；BE1 和BE2 為參考光和物光的擴束透鏡系統（由物鏡、小孔光闌和準直透鏡組成）。 實驗光路實物如圖4 所示。

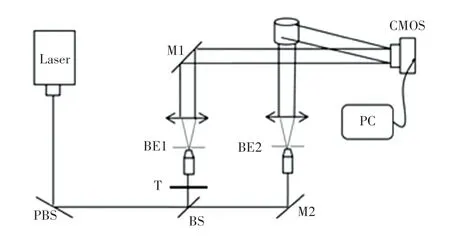
圖3 離軸數字全息光路示意圖Fig. 3 Schematic illustration of off-axis digital hologram

圖4 實驗光路圖Fig. 4 Diagram of the experimental light path

首先，在液晶波片不加電壓時記錄一幅數字全息圖，之后通過對液晶波片施加電壓產生移相后再次紀錄一幅全息圖。 此過程僅通過電壓改變了液晶波片的延遲量，而不需要進行其它機械操作，響應時間為10 ms 左右（如采用鐵電相的液晶波片，響應時間可減小為100 μs 左右）［15］。 對記錄的原始全息圖進行菲涅爾再現，獲得其頻域圖和再現像如圖5所示。 其中圖5（a）記錄的是全息圖。 圖中橫向和縱向的條紋是光路間激光來回反射所造成，可通過對全部光器件增加增透膜來降低。 圖5（b）是全息圖的頻域信息。 可以看到零級項能量最高對物體信息有一定的干擾。 圖5（c）是全息圖的重建像，零級像衍射造成的干擾十分明顯，因此在頻域濾波再現。 圖5（d）中圖像信噪比較低，從而導致成像質量較差。

如在公式（8）中進行相移后，對兩幅全息圖進行處理得到的頻域圖和再現像，如圖6 所示。 其中6（a）是處理后全息圖的頻域信息，可以明顯的看到零級項得到很大程度的抑制。 相比圖5（b），再現像（b）中的零級像產生的干擾大大降低。 因此，結合頻域濾波再現圖（c）的質量得到很大的提升。

從上述實驗結果對比可以明顯看到，零級項對物體信息有很大的干擾，頻域中零級項占據大部分的能量，導致物體信息噪聲較多。 本文提出的方法對于去除零級項的效果較為明顯，在真實項被零級噪聲淹沒的條件下，仍可以較好的恢復出物體信息，使物體信息的質量得到很大的改善。 對于圖6（b）中存在的少量殘余直流分量，主要是對液晶兩次相移前后外界的實驗環境有所變化所造成，可采用維納濾波［16］去噪和提高系統穩定性等方式來減小殘余的直流分量。從圖5（d）和圖6（c）的對比中可以看出，雖然本文采用的是離軸全息成像系統，但實驗的結果同樣降低了直流分量對再現物理信噪比的影響。 所以，本文提出的去除直流分量的方式同樣適用于同軸全息成像系統。

通過控制液晶固定的延遲量可以產生0，π／2，π和3／2π 等相移［17］，利用該結果可進行全息成像系統兩步、三步和四步的移相研究，從而在共軛像的去除、四步相移去相位包裹、移相剪切散斑干涉成像等領域將會得到較好的應用。 由于本文采用的是向列相液晶，其響應時間為10 ms 左右，所以提出的該方案在實時三維全息的成像系統中也可以得到較好的應用。

3 結束語

本文通過電控液晶波片在參考光路中引入一次任意相移的方式，記錄了兩幅全息圖。 此系統不需要進行額外的進行機械操作，有較好的穩定性，且對移相不需要精確的相位值，數據處理簡單。 通過采用一次任意相移法結合頻域濾波法，有效地消除了全息圖中的零級干擾，得到了基本沒有干擾的再現像，對圖像的質量有較大的提升。 由于該方法可以直接消除零級項，所以也適應于記錄相機分辨率較低、拍攝夾角較小的全息系統，而導致零級項和真實項重疊的情況也可以適用。 相信本文的結果將對實時三維成像的數字全息系統、等相關領域得到較好的應用。