管樁預應力自動張拉機張拉部件的優化設計與疲勞壽命分析

湯 亮， 杜衛東， 龔發云， 李飛揚

(1.湖北工業大學機械工程學院， 武漢430068； 2.湖北省制造業創新方法與應用工程技術研究中心， 武漢430068)

預應力混凝土技術在建筑結構等領域應用非常廣泛[1-2]。管樁預應力張拉機是一種預應力管樁生產的主要設備，它為管樁鋼筋籠施加預應力，保證管樁獲得良好的力學性能和產品質量。隨著城鎮化的加速，對預應力混凝土產品的質量和產量有越來越高的要求。實踐表明，管樁生產過程中，張拉機長期處于頻繁啟動、制動以及重復變幅載荷的狀態，長期反復的重載荷作用可能引起機械系統故障，甚至導致零部件疲勞失效，嚴重影響管樁產品的質量，給企業帶來巨大的安全隱患和經濟損失[3-4]。近年來，在預應力張拉機設計方面有一些研究。任磊[5]為了減少軌道板的裂紋，增加軌道板的使用壽命,對張拉部件進行了有限元分析，設計了高鐵軌道板預應力筋自動張拉。劉瑞東[6]設計預應力水泥電桿張拉機，提高了水泥張拉生產自動化程度，保證了張拉的準確度。在張拉部件優化和疲勞壽命預測的研究較少，因此為了有效地降低張拉部件疲勞斷裂引起的安全事故的發生率，和保障工作人員生命以及財產安全，對優化設計方案進行疲勞壽命預測顯得至關重要。

疲勞壽命預測方法一直是機械裝備設計領域研究的熱點[7-9]。由于實際零件的載荷多為變幅載荷，其具有隨機性且難以準確獲取，為了分析變幅載荷的疲勞壽命，學者們提出了一些變幅載荷疲勞壽命預測的方法。有的學者提出了理論模型，進行變幅載荷疲勞壽命預測。徐國建等[10]根據Miner理論，通過對恒幅載荷條件下應力幅與壽命之間的關系的隨機化處理，提出了用于隨機變幅載荷下疲勞可靠性分析的RDCDR模型。趙少汴[11]根據Miner理論簡化實際零件受到的變幅載荷，只認為峰值和谷值對壽命起作用，將變幅載荷看作是若干個恒幅載荷的組合。也有的方法是基于實驗進行變幅載荷的疲勞壽命預測。Sonsino等[12]通過對比試驗，研究了變幅載荷與恒幅載荷的疲勞壽命，得出變幅載荷疲勞壽命高于峰值的恒幅載荷疲勞壽命，因此施加恒幅載荷得到的壽命結果較為保守。盧耀輝等[13]通過車輛系統動力學計算獲得車體隨機載荷譜，基于FKM標準和有限元法對高速列車進行疲勞壽命分析。還有的方法是基于有限元分析進行變幅載荷的疲勞壽命預測。盧黎明等[14]利用ABAQUS動力學仿真分析結果生成變幅載荷譜，基于nCode Design-Life對滾滑軸承疲勞壽命進行了預測。

現以提高系統的響應速度為目標對張拉部件進行輕量化設計；根據Miner理論簡化實際零件受到的變幅載荷，通過將變幅載荷轉化為峰值的恒幅載荷來分析其疲勞壽命；由易損傷點位置的分析進一步明確了優化方案，并對比分析了優化前后的疲勞壽命。與傳統實驗法進行疲勞壽命分析相比，此方法縮短了前期設計周期以及為進一步優化設計提供一定的安全空間，是一種高效實用的方法。

1 張拉部件結構優化設計

1.1 張拉部件結構設計

管樁預應力自動張拉機整體方案如圖1所示，主要由管徑檢測傳感器、鎖螺母裝置、張拉部件、千斤頂、垂直升降臺、控制柜和水平位移小車組成。管樁預應力自動張拉機的基本工作原理：張拉機自動調整位置與管樁模對接，其千斤頂活塞收縮將預應力傳遞給管樁模內部的鋼筋籠。考慮到張拉機使用環境和功能要求，其執行端部件主要完成自動對接和張拉兩個動作，因此設計了合抱式張拉部件。張拉部件主要包括卡爪、位置傳感器1、張拉桿、液壓缸、轉軸、位置傳感器2、基座和拉桿。張拉部件具體結構如圖2所示，張拉機對接和張拉過程中，首先張拉桿接觸到位置傳感器1產生限位信號，兩個液壓缸推動兩個卡爪合抱張拉桿；接著兩個卡爪合攏時觸發位置傳感器2產生信號，表明對接已完成；最后液壓千斤頂活塞收縮，通過張拉部件將預應力傳遞給管樁模內部的鋼筋籠。

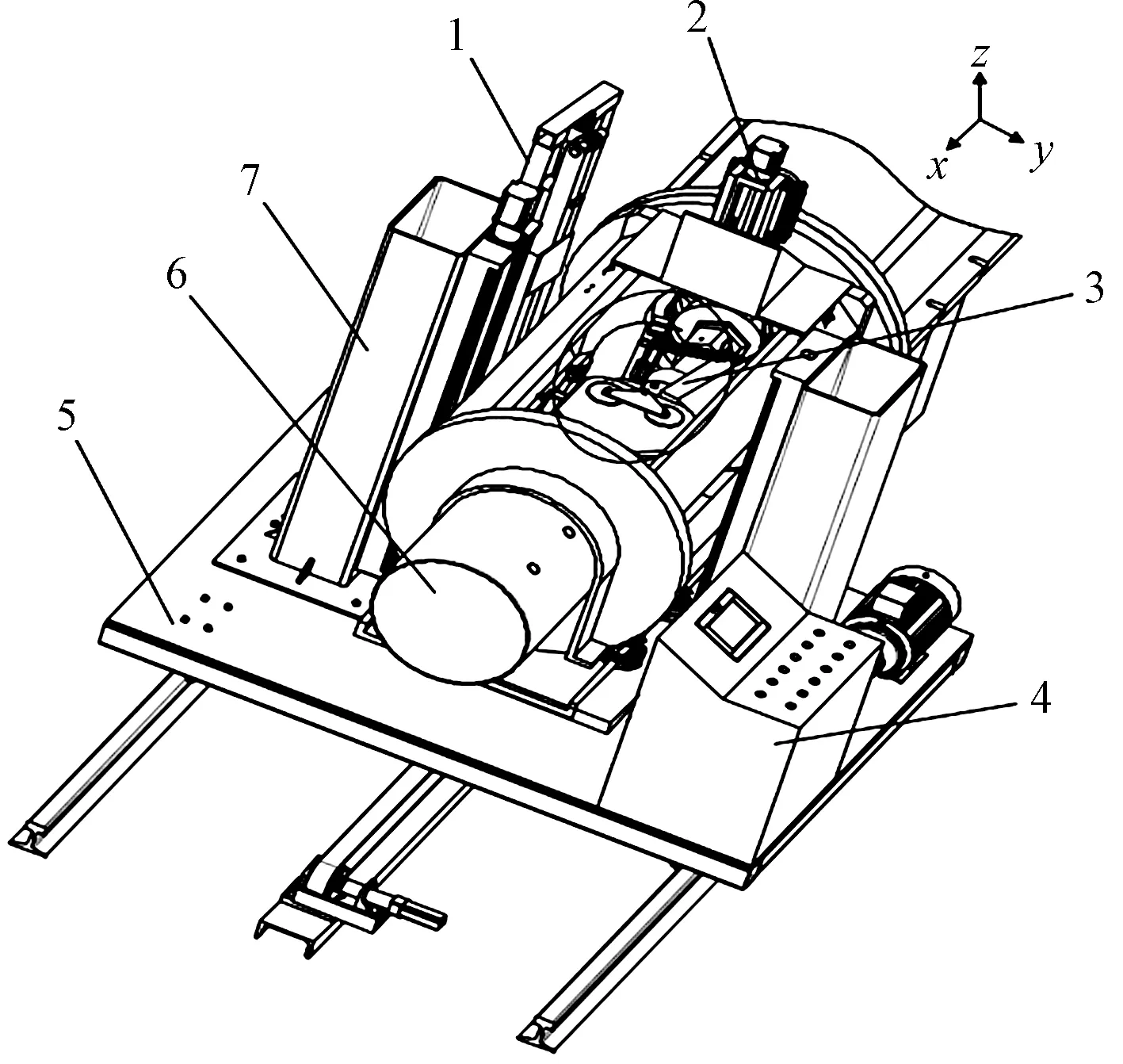
1為管徑檢測傳感器；2為鎖螺母裝置；3為張拉部件；4為控制柜；5為水平位移小車圖；6為千斤頂；7為垂直升降臺圖1 管樁預應力自動張拉機整體方案Fig.1 The general scheme of prestressed pipe automatic tensioning machine

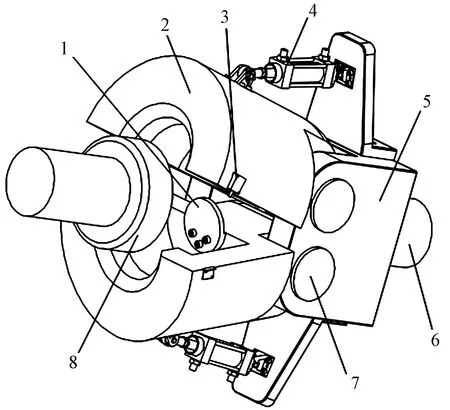
1為位置傳感器1；2為卡爪；3為位置傳感器2；4為液壓缸；5為基座；6為拉桿；7為轉軸；8為張拉桿圖2 張拉部件結構示意圖Fig.2 Structural sketch of tensioning components

1.2 活動零件卡爪的靜力學分析

張拉部件是管樁預應力張拉機的重要執行端，其中卡爪是關鍵的執行零件，卡爪的力學性能與張拉部件的壽命有密切關系，因此有必要進行靜力學分析。E級鋼是廣泛應用于火車車鉤的材料，其各項強度幾乎是45鋼的2倍，因此，采用E級鋼可以更好地提升張拉部件整體的工作性能[15-17]。根據卡爪使用的要求，分析得到卡爪主要承受拉力，因此利用第一強度理論分析計算得出初始尺寸。在Solidworks中建立卡爪的三維模型，導入到ANSYS Workbench中，定義卡爪的材料屬性為E級鋼，其彈性模量E=2.15×1011Pa，泊松比為0.3，密度為7 050 kg/m3。采用四面體單元Solid186將模型進行網格劃分。張拉機在張拉過程中最大的張拉力為300 t，每一個卡爪受到的拉力最大為1 470 kN，因此在卡爪一端設置固定約束，另一端施加大小為1 470 kN的拉力，得到卡爪的加載模型，如圖3所示。有限元模型進行求解可以得到卡爪應力云圖，如圖4所示。

圖3 卡爪有限元模型Fig.3 Finite element model of connector

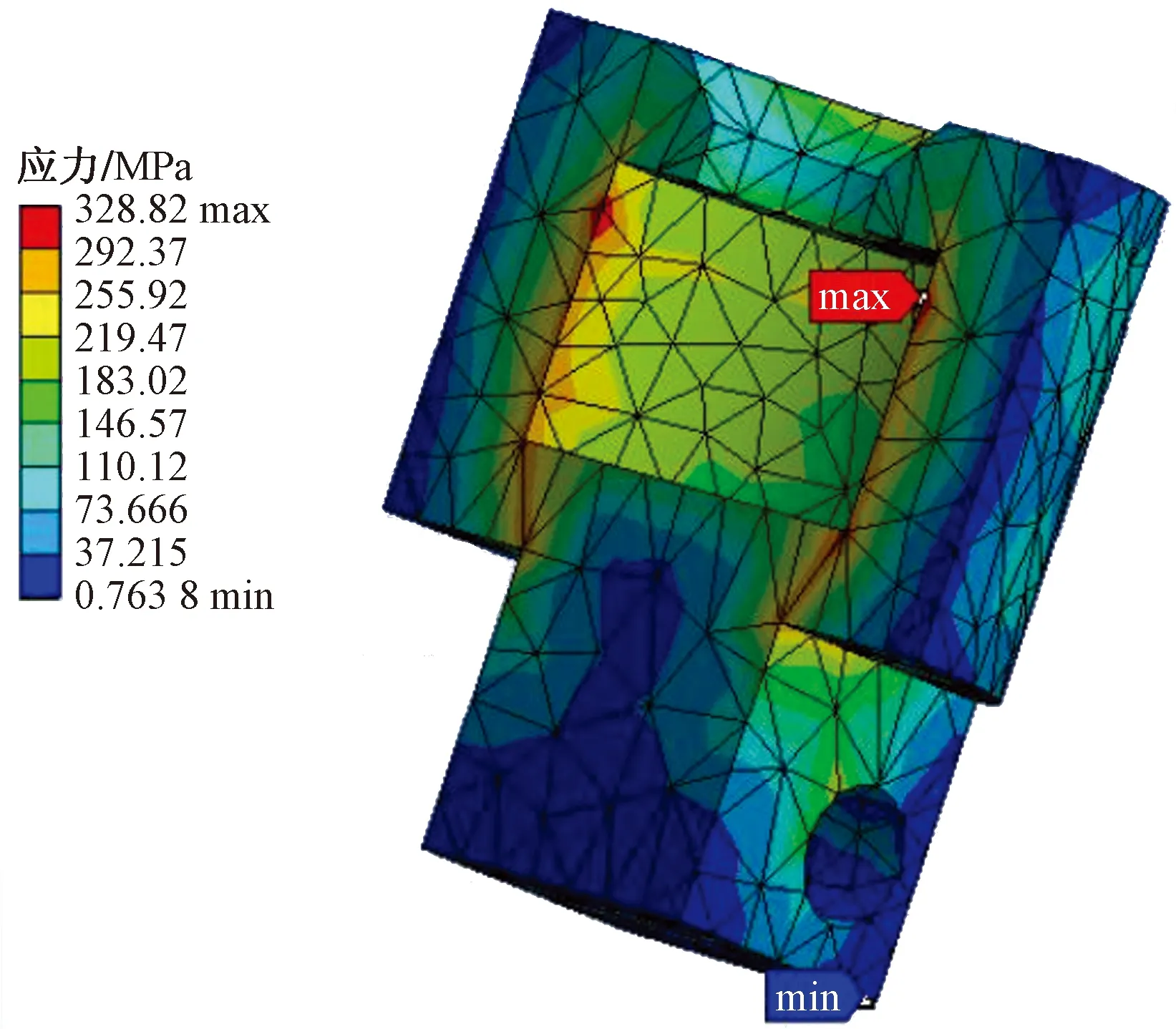
圖4 卡爪應力云圖Fig.4 Stress nephogram of connector

由有限元求解結果可知，活動零件卡爪的最大應力為328.82 MPa，小于材料的屈服極限690 MPa，滿足其強度要求，其質量有較大的盈余，慣性過大，不利于執行機構的控制，嚴重影響了張拉執行系統響應的速度，因此活動零件卡爪必須進行輕量化設計。

1.3 卡爪尺寸優化設計

根據張拉部件的工作和裝配要求，選取卡爪截面尺寸D1、D2、D3、L1作為優化設計變量X。卡爪的結構特點可知，可以將以質量最小為目標簡化為以剖面的面積S最小為優化目標，ε為最大變形量，σmax為最大應力，可以得到尺寸優化數學模型，如圖5所示。

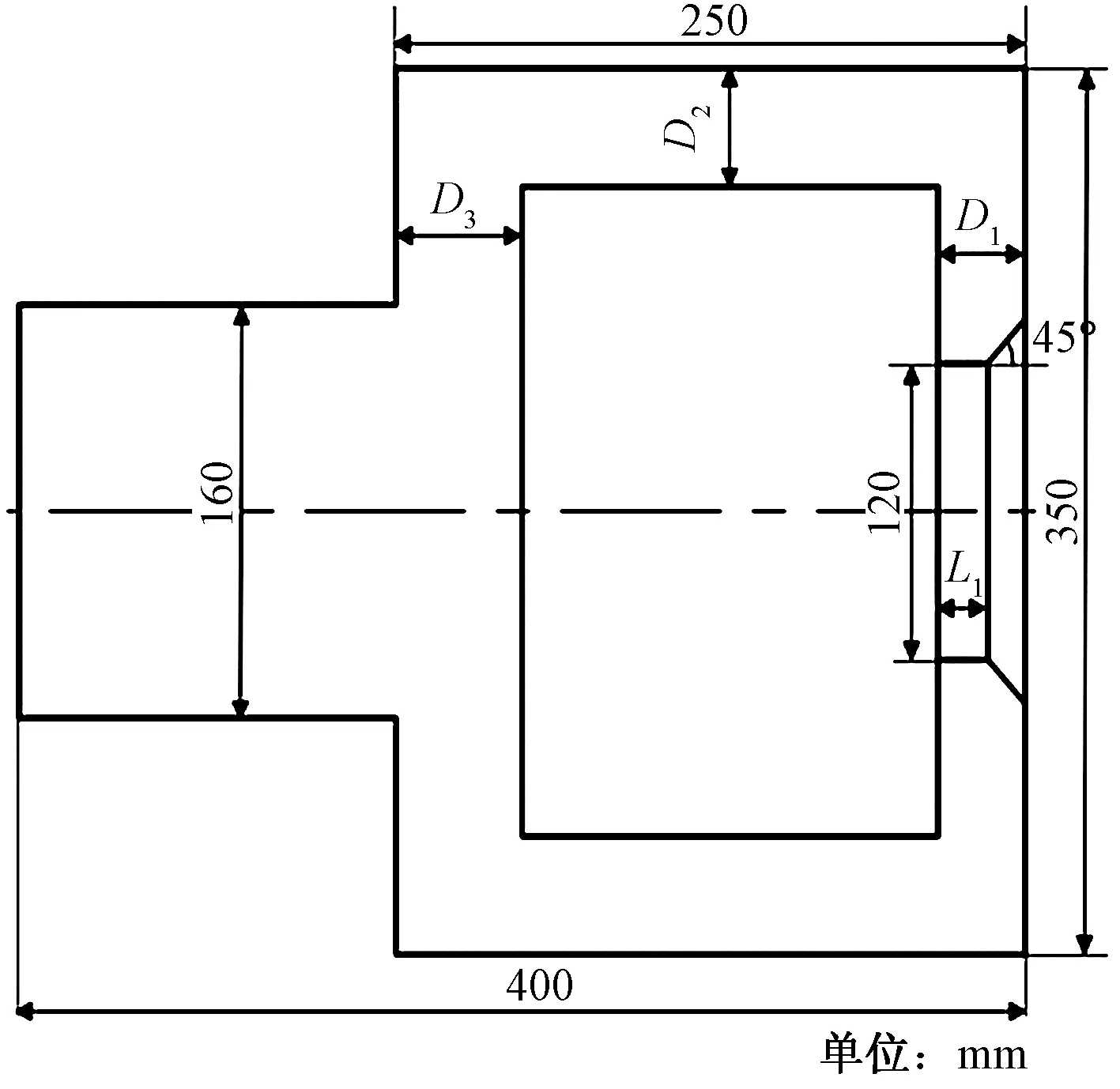
圖5 尺寸優化數學模型 Fig.5 Mathematical model of size optimization

根據活動執行端卡爪的活動空間范圍及其強度與剛度要求，確定優化的約束條件為

X=(D1，D2，D3，L1)T，

minS=24 000+350D1+500D2+350D3-

2D2(D1+D3)-120L1-(D1-L1)2，

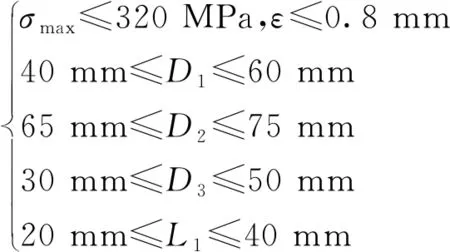
(1)

由活動零件卡爪優化數學模型可知，約束函數是設計變量的隱函數，因此其優化算法必須結合有限元分析才能進行優化求解。利用ANSYS Workbench中的Goal Driven Optimization模塊，基于有限元分析結果的響應曲面算法，采用Kriging法能夠準確高效地得到上述卡爪優化數學模型中隱函數的解集。以卡爪截面尺寸D1、D2、D3、L1作為輸入變量，根據邊界條件，輸入變量D1取40～60 mm，D2取65～75 mm，D3取30～50 mm，L1取20～40 mm，以卡爪的質量m、最大應力σmax、最大變形量ε為輸出變量，并設置面積最小為目標函數，以σmax<320 MPa、ε<0.8 mm為約束條件，Workbench給出3組最佳的優化解，如表1所示。

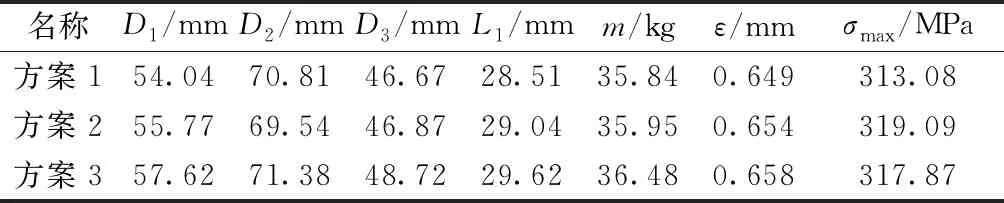
表1 最佳的優化解

綜合考慮卡爪輕量化與強度剛度要求，選擇方案1為最優設計方案，將方案1進行圓整，即取D1=54 mm、D2=70 mm、D3=46 mm、L1=28 mm，作為最終優化方案。最終優化方案進行靜力學分析，結果如表2所示。

利用拓撲優化的分析，結果如圖6所示，得出卡爪質量還有較大的盈余，同時考慮到其執行動作時的干涉問題，于是卡爪結構進一步優化，即圓角處理。

表2 優化前后結果對比

圖6 拓撲優化 Fig.6 Topological optimization

得到優化結果：圖7為再優化有限元模型，圖8為再優化應力云圖。由圖7、圖8可以得到，最大應力為219.69 MPa，遠遠小于材料的屈服強度。最終質量為33.524 kg，質量總體減少了16.75%，從而減少了執行系統的慣性力，提高了響應速度，提高了張拉機的工作性能。

2 張拉部件靜力學分析

2.1 建立張拉部件有限元模型

考慮到張拉部件實現的功能和強度要求，分析各個零部件的受力情況，根據不同的受力情況分別采用第一強度理論和第三強度理論分析計算得出零部件的重要尺寸，結果如表3所示。

圖7 再優化有限元模型Fig.7 Reoptimization finite element model

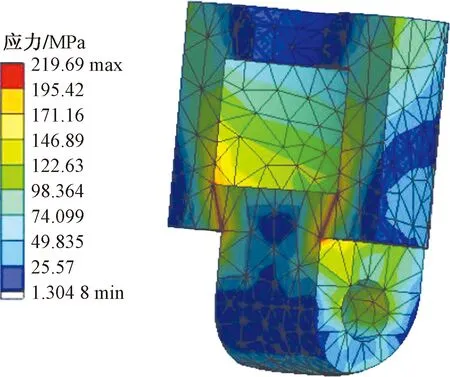
圖8 再優化應力云圖Fig.8 Re-optimizing stress nephogram

表3 張拉部件主要參數

為了真實有效地反映其疲勞損傷和疲勞壽命情況，采用整部件模型分析，轉軸與基座采用剛性連接，卡爪與轉軸采用鉸關節連接，并考慮到卡爪與張拉桿的緊扣連接。為了便于有限元分析，需要將結構簡化，因此可以忽略影響較小的因素，利用表3中的數據建立張拉部件有限元簡化模型，結果如圖9所示。在預應力張拉時，兩卡爪處于完全閉合狀態，張拉力是沿Z軸方向，考慮到在此狀態下張拉部件承受全部的張拉力300 t。張拉部件結構分析計算主要需要考慮的載荷類型是張拉工作載荷，其峰值為最大張拉預應力2 940 kN，因此以最大張拉預應力為承受載荷進行靜強度分析。

在ANSYS Workbench中進行有限元靜力學分析，采用四面體單元網格劃分，完整的卡爪、轉軸、基座和后張拉桿網格劃分，網格劃分結果如圖10所示，單元最小尺寸為10 mm，包含單元數67 062個，節點數116 118 個。

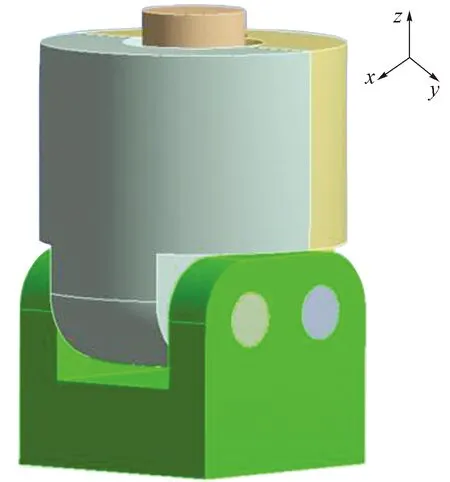
圖9 張拉部件有限元簡化模型 Fig.9 The simplified finite element model for tension parts

圖10 張拉部件網格劃分結果Fig.10 Meshing results of tensioning parts

2.2 張拉部件靜強度分析

通過有限元分析得到應力云圖，如圖11所示。

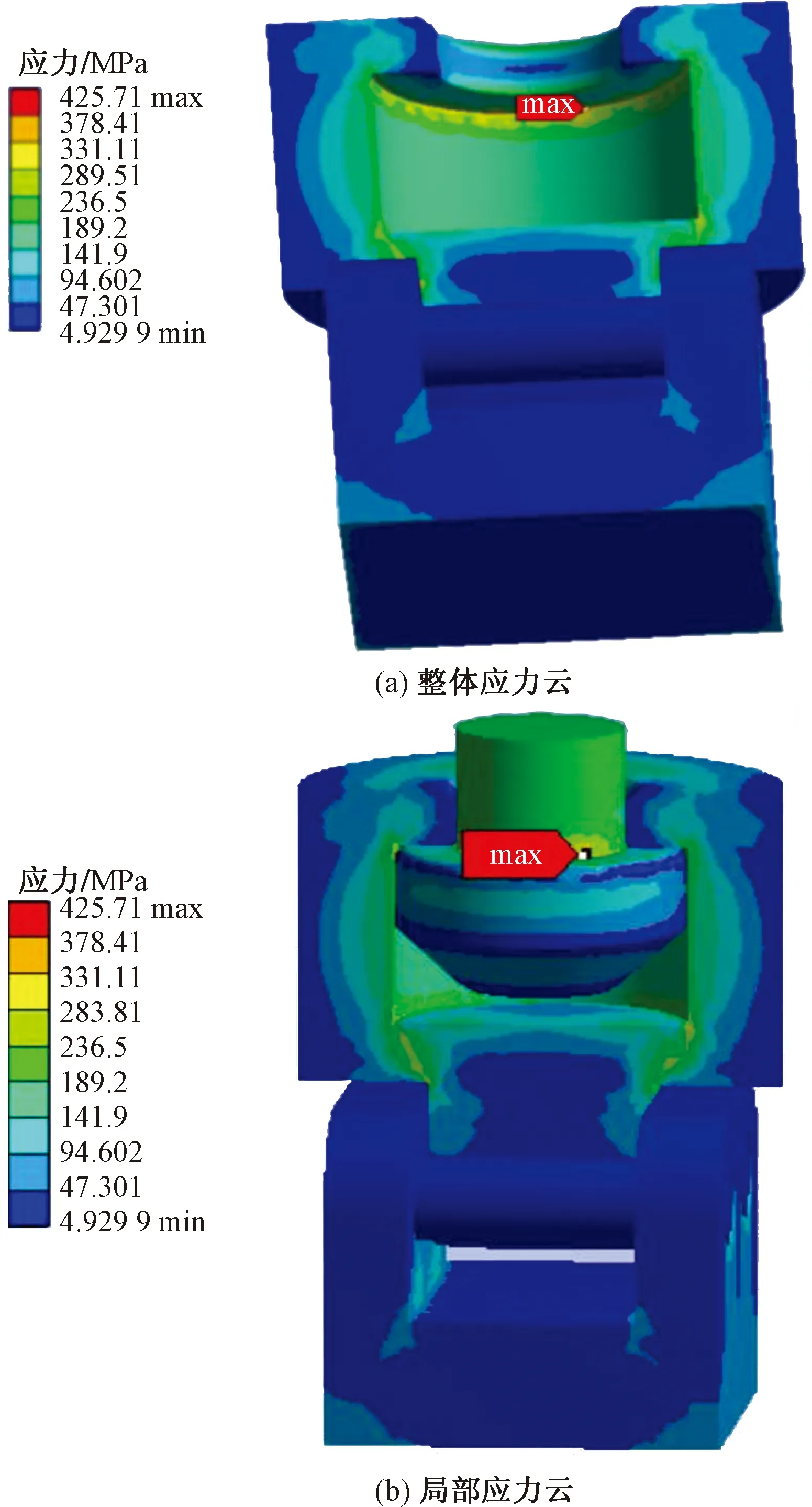
圖11 張拉部件應力云圖Fig.11 Stress nephogram of tensioning parts

從有限元分析結果得出，最大應力為425.71 MPa，遠小于材料的屈服極限強度690 MPa，位于卡爪形狀突變位置和張拉桿的軸肩處，并且在最大應力附近的應力分布梯度較大，應力集中非常顯著。

3 張拉部件疲勞分析

3.1 獲取載荷時間序列

張拉部件作為張拉機的重要執行端，長期承受重復變幅載荷，是常常疲勞破壞的部件。依據ANSYS Workbench靜力分析結果得到最大應力小于屈服極限強度，以及疲勞類型分類，確定該張拉部件屬于應力為主導的高周疲勞類型，因此選擇應力疲勞(S-N)分析方法[18]。基于ANSYS Workbench有限元靜力學分析結果，利用總應變壽命方程基本原理和Miner理論，采用nCode Design-Life專業疲勞壽命仿真分析軟件[19]，對張拉部件進行疲勞壽命預測。

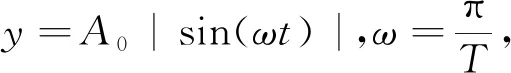
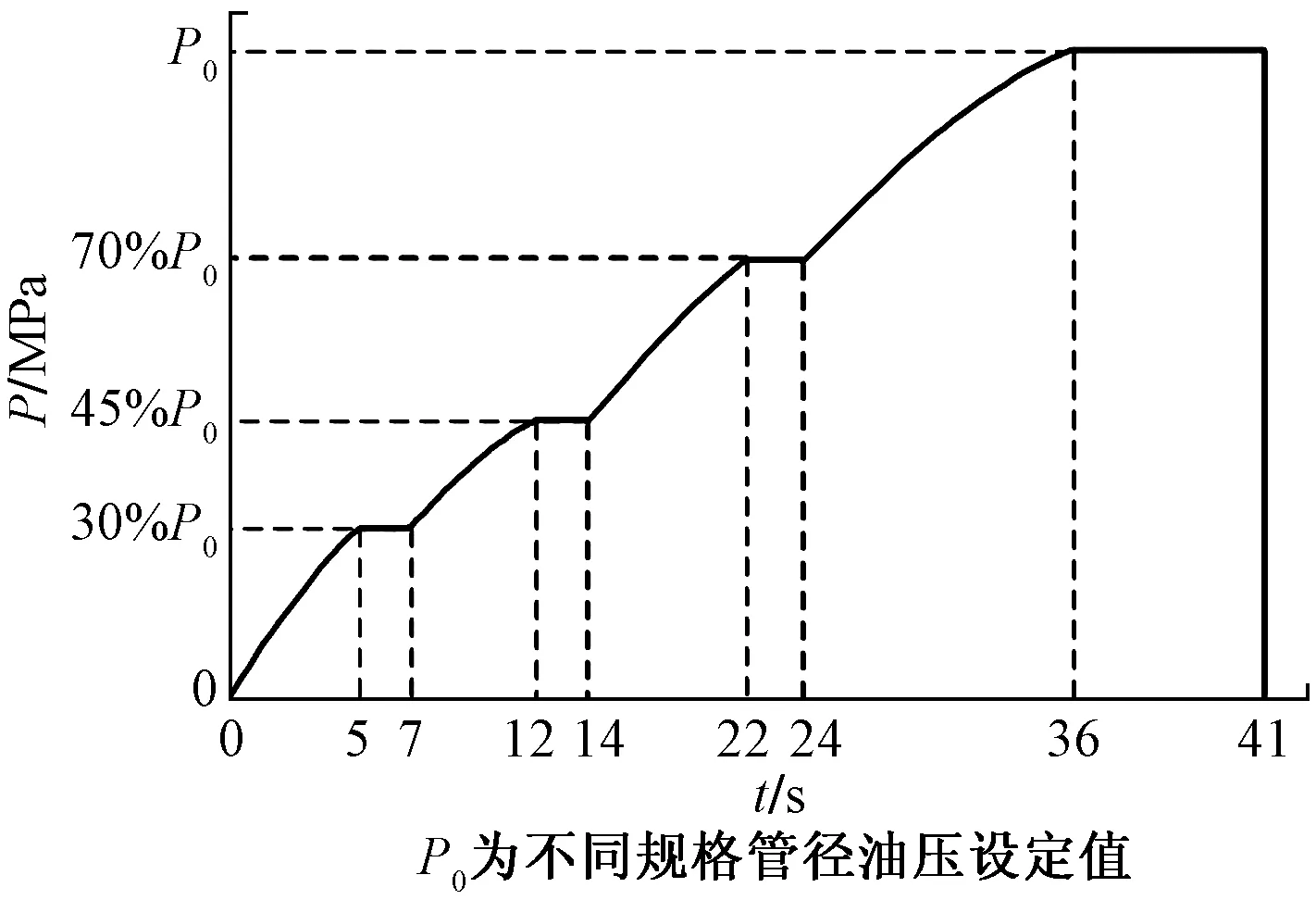
圖12 張拉曲線的加載階段Fig.12 Loading stage of tension curve

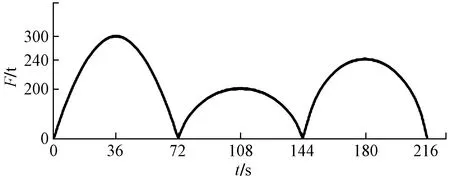
圖13 簡化后的張拉載荷Fig.13 The simplified tension load

載荷時間序列反映了零部件所受載荷隨時間的變化情況，其與靜載荷結果相映射作為疲勞壽命分析的循環載荷譜。根據張拉機的載荷范圍和擬合的張拉曲線，需要確定最大值的恒幅載荷時間序列。以最大峰值300 t為例編制載荷時間序列，0.1 s間隔為步長，利用MATLAB編制計算程序，得到載荷時間序列文件。將載荷時間序列文件輸入nCode Design-Life中，繪制得到一個作業循環的載荷時間序列曲線，如圖14所示。

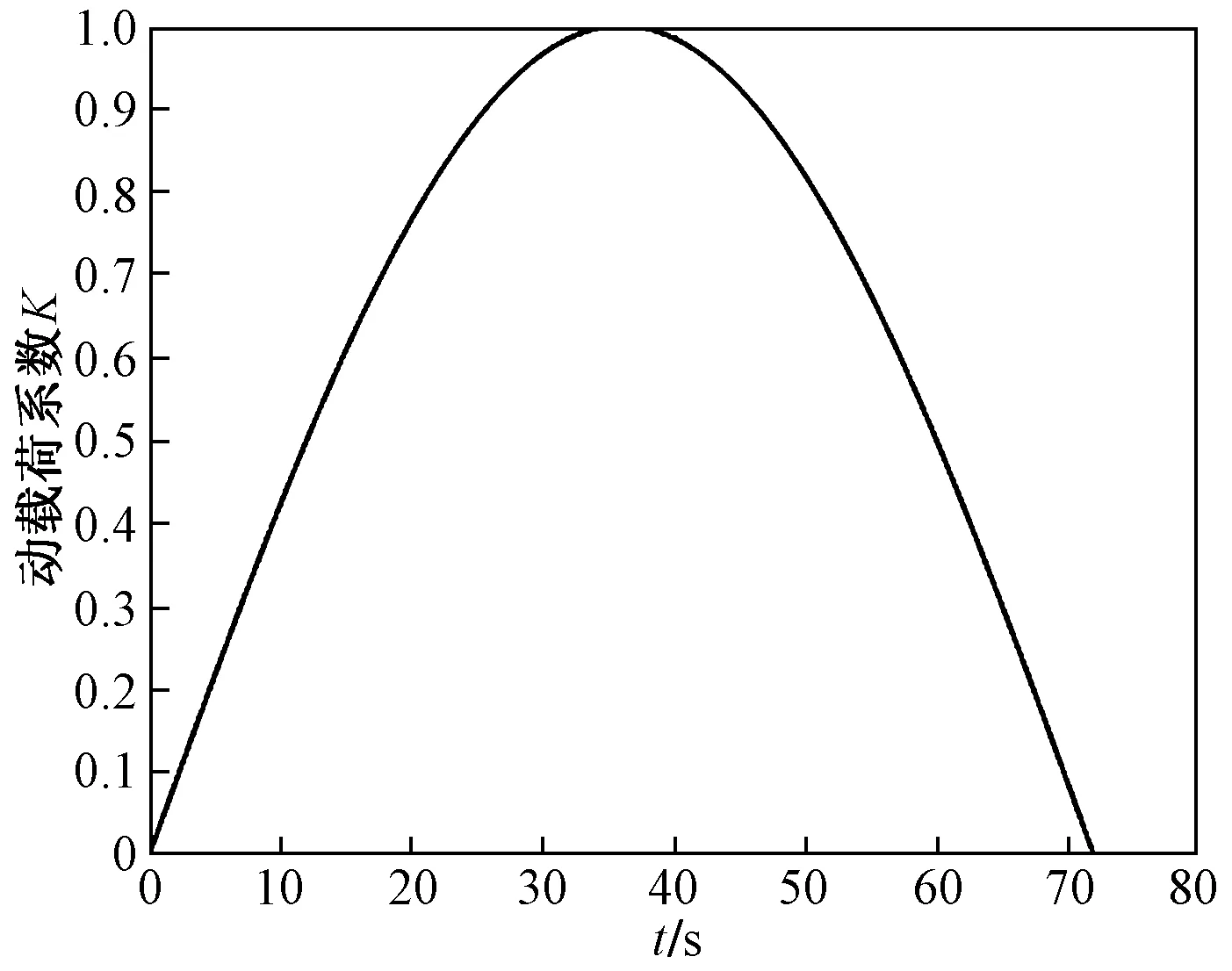
圖14 300 t載荷時間序列曲線Fig.14 Time series curve of 300 tons load

3.2 材料設置

為了精確地預測疲勞壽命，必須保證材料參數的準確性。該張拉部件所用材料均采用屈服強度為690 MPa的E級鋼。國家標準提供的材料壽命參數是通過標準試棒測得的數據，實際零件與標準試棒的形狀差別較大，以及考慮到使用環境和載荷狀況等多種影響因素，需要將材料壽命數據進行等效處理，因此對標準的S-N曲線進行修正，才可以進行精確的疲勞壽命計算。采用Soderberg理論進行修正，得到材料修正后的S-N曲線，結果如圖15所示。

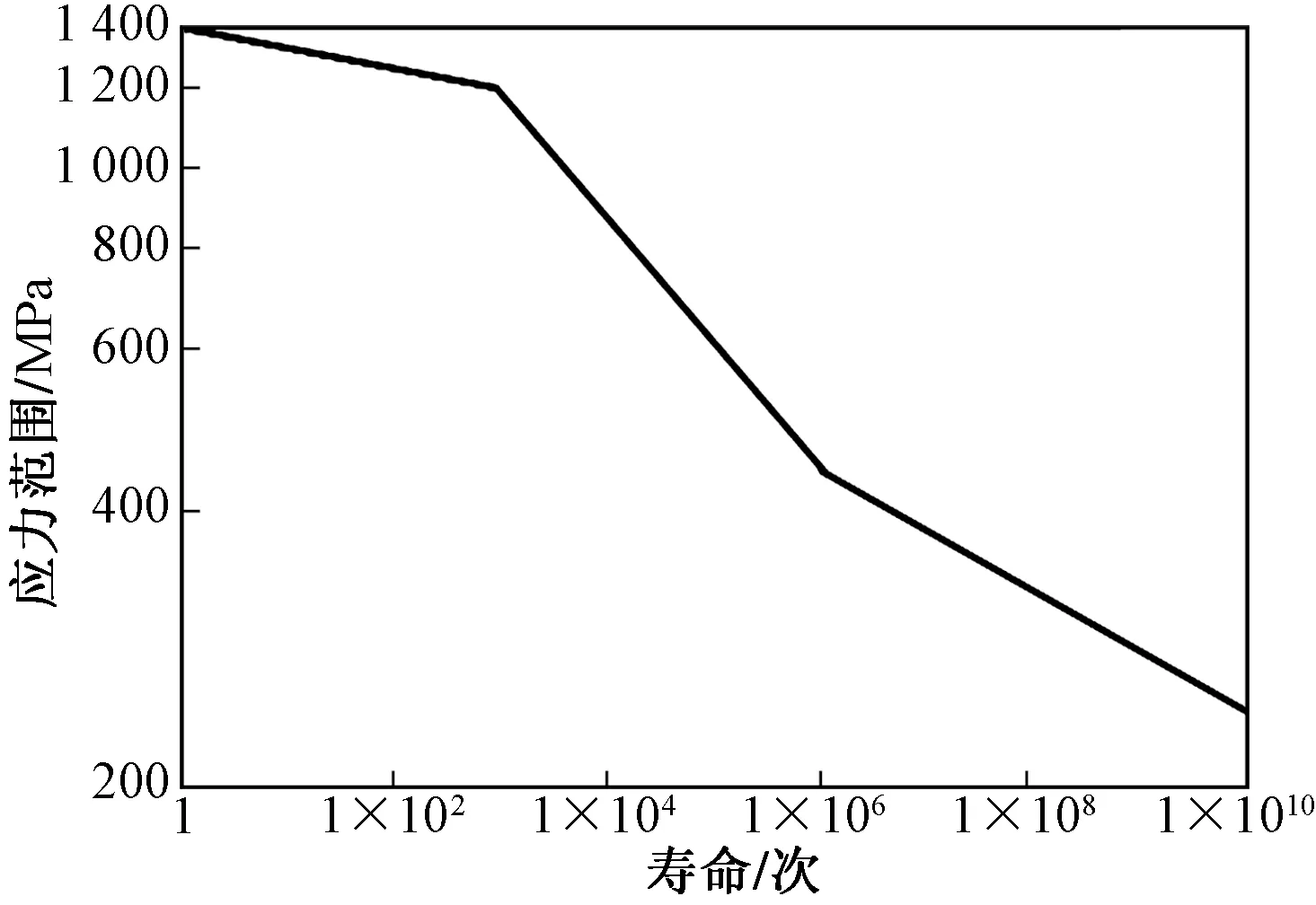
圖15 修正后S-N曲線Fig.15 The corrected S-N curve

3.3 疲勞預測分析

將ANSYS workbench靜力學的分析結果與nCode Design-Life連接進行聯合仿真，創建材料和載荷譜的映射，設置求解參數，利用有限元計算得出疲勞損傷云圖和壽命云圖。最大峰值恒幅載荷疲勞壽命云圖和損傷云圖，如圖16、圖17所示。

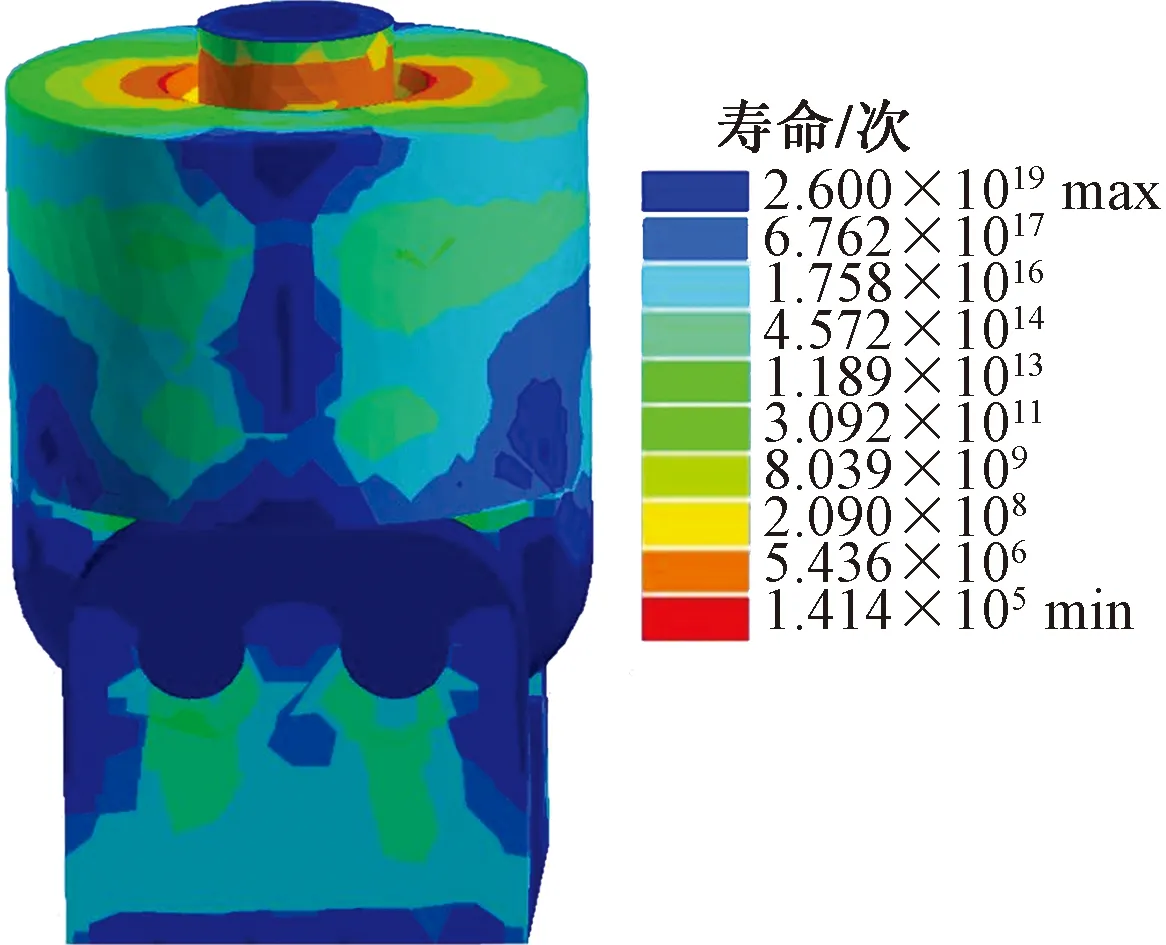
圖16 最大峰值恒幅載荷疲勞壽命云圖 Fig.16 Fatigue life nephogram of maximum peak constant

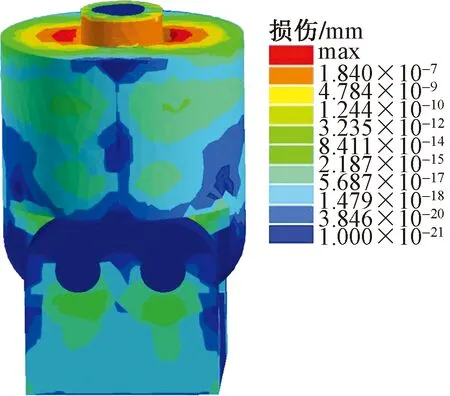
圖17 最大峰值恒幅載荷疲勞損傷云圖Fig.17 Fatigue damage nephogram of maximum peak constant

根據圖16、圖17，考慮到生產效率和8 h工作制，以及張拉機準備時間得出每月循環次數為4 000 次，進而計算出張拉部件的壽命。在變幅載荷作用下，張拉部件絕大多數部位循環次數均大于1.77×105次，最大損傷值為7.07×10-6mm，疲勞循環次數為1.41×105，其壽命為2.95年。

3.4 最易損傷位置分析

通過在nCode Design-Life中的glyph區域中添加hot模塊，可以得到最傷點位置及其損傷情況，如表4為在最大峰值恒幅循環載荷條件下10個最易損傷點的疲勞壽命情況。

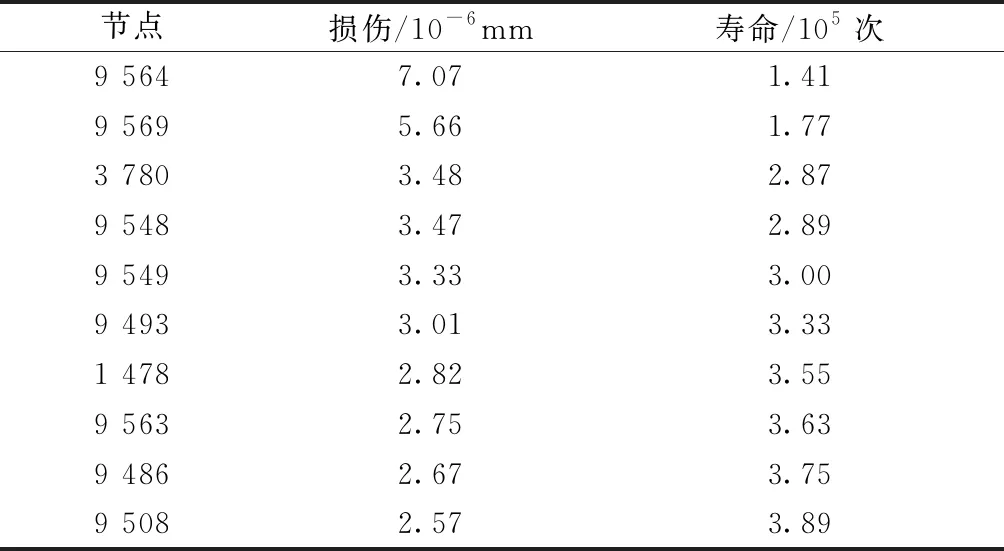
表4 疲勞損傷最大節點處疲勞壽命及損傷大小

4 張拉部件再優化以及壽命預測分析

機械結構的變截面處，在外部載荷作用下往往會出現應力集中, 易出現疲勞失效[20]。通過易損傷位置的分析，針對張拉部件的連接處應力集中問題，得出在連接處極易產生裂疲勞紋和破壞，因此提出了在卡爪和張拉桿的應力集中處增大圓角以提高張拉部件疲勞強度的方法，如圖18所示。

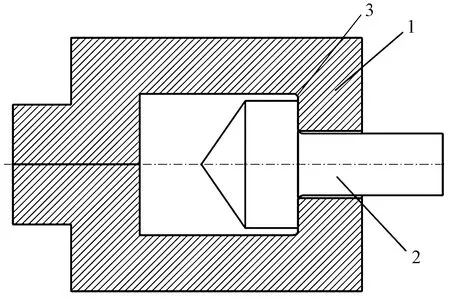
1為卡爪；2為張拉桿；3為圓角處圖18 卡爪與張拉桿連接處增大圓角處理Fig.18 Increased the roundness at the joint of connector and tensioning rod

通過表4確定張拉部件的易損傷位置，可以為在包括材料等其他基本因素相同的條件下建立有限元模型，以載荷峰值300 t為例，利用ANSYS Workbench中進行靜力學分析，結果如圖19所示。圓角前后結果對比如表5。由應力云圖可知最大應力為388.91 MPa，與結構優化前相比最大應力減小了，并且最大應力節點附近應力分布梯度較小，因此應力集中有了明顯改善。根據上述的疲勞分析流程圖以及載荷時間序列曲線，基于結構優化后的靜力學分析結果進行疲勞壽命分析，結果如圖20所示。

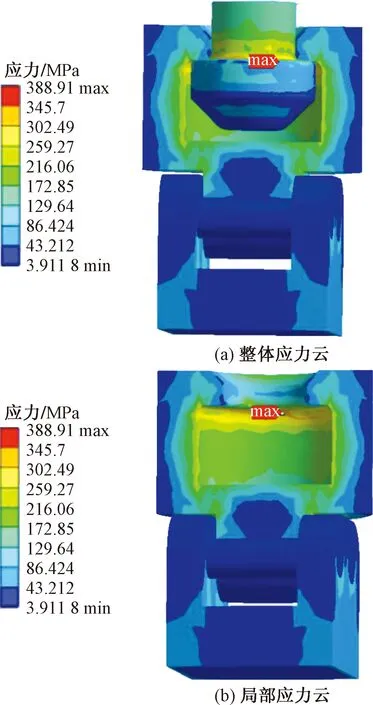
圖19 張拉部件結構再優化應力云圖Fig.19 Stress nephogram of re-optimizing structure of tensioning parts

表5 圓角前后結果對比

分析最大峰值恒幅循環載荷疲勞壽命云圖可知，在載荷作用下循環次數為1.78×105次，因此該張拉部件的壽命為3.41年，比優化前的疲勞壽命提升了15.5%。通過對比優化前后的疲勞壽命，得到采用大圓角的方法可以改善應力集中的狀況，以及提高疲勞強度，為新一代張拉部件優化設計提可靠的理論依據。

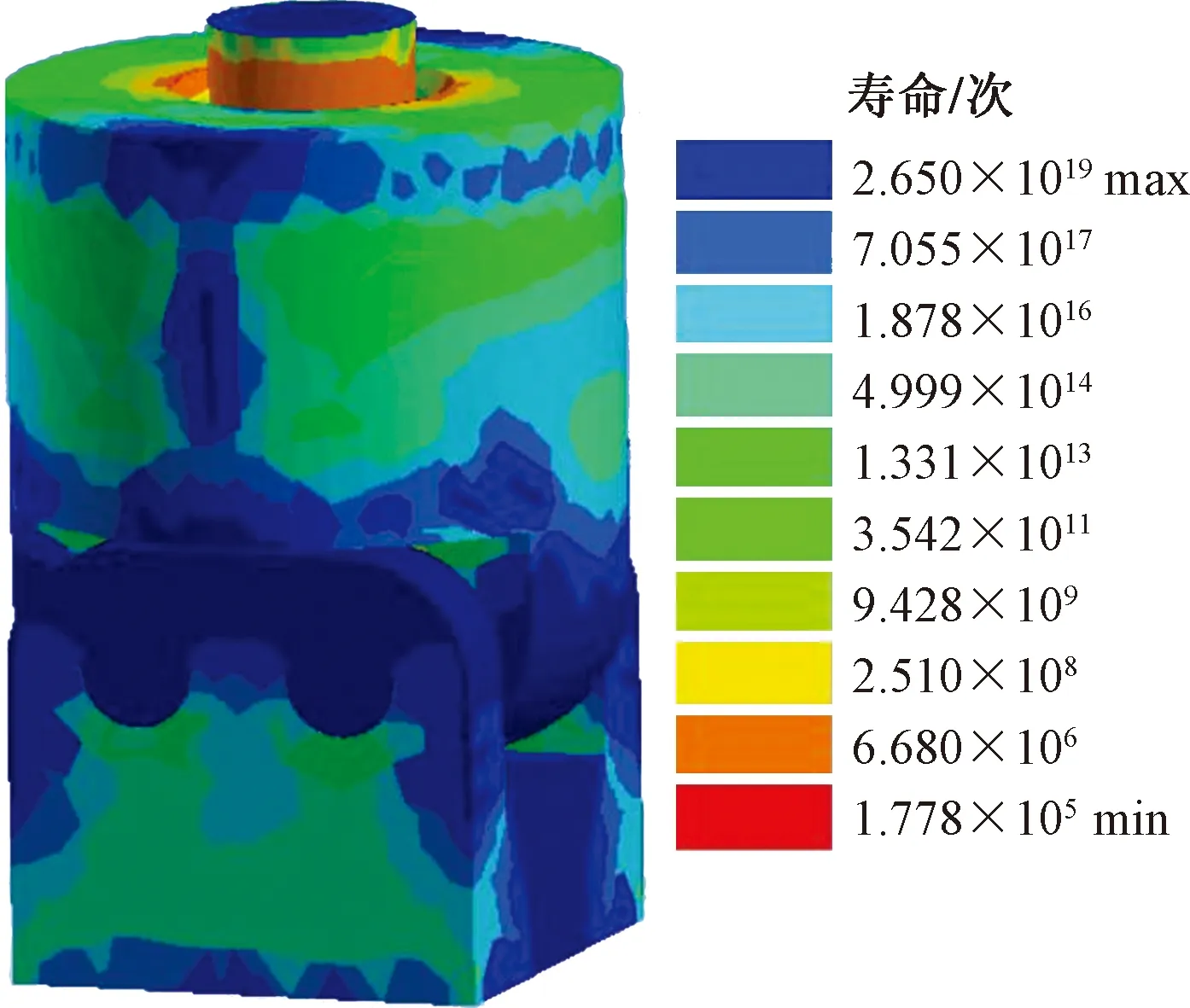
圖20 張拉部件結構再優化壽命云圖Fig.20 Life nephogram of re-optimizing structure of tensioning parts

5 結論

(1)為了解決張拉機笨重導致加載滯后時間過大的問題，設計了合抱式張拉部件，同時對活動零件卡爪進行了優化設計與輕量化設計，改善了張拉機的工作性能，為新一代張拉機的設計制造提供了思路。

(2)基于有限元靜力學分析結果，利用nCode Design-Life疲勞仿真軟件建立疲勞分析流程圖，將變幅載荷轉化為峰值的恒幅載荷條件來進行疲勞壽命預測，分析張拉部件損傷云圖和壽命云圖，從而得出變幅載荷條件下張拉部件的疲勞壽命范圍。與傳統實驗法進行疲勞壽命分析相比，此方法縮短了設計周期和減少了成本。

(3)張拉機關鍵執行端張拉部件受到的變幅載荷具有隨機性，其疲勞壽命具有較大的離散性，且在前期優化設計中變幅載荷曲線難以準確獲取，基于峰值的恒幅載荷疲勞壽命結果較為保守，利用鋼筋拉伸曲線將變幅載荷轉化為最大峰值的恒幅循環載荷條件下的疲勞壽命預測，利用這一結果為零部件優化設計預留安全空間，可以為張拉部件的設計提供參考。