讓思考更“進”一步

程利青

摘要：探索活動是學生探索規律、積累數學活動經驗的過程。教學中，教師要把新舊知識有機整合，練中有變，變中有比，比中求深，層層遞進;促使學生不斷超越具體知識和技能，深入到思維的層面，由具體的數學方法和策略過渡到一般性的思維策略，促進學生思維品質的提升，使其養成有根據、有條理、有深度的思考習慣。

關鍵詞：數學活動經驗 ?思維方式 ?思考習慣

北師大版《數學》六年級下冊第一單元實踐活動課內容為：準備六張長16 cm、寬4 cm的長方形紙。做一做，想一想。

（1）取出2張長方形紙，一張橫著卷、另一張豎著卷，卷成的圓柱形體積一樣大嗎？猜一猜，算一算。（保留2位小數）

（2）再取出2張長方形紙，照樣子做一做。

……

“用6張完全一樣的長方形紙卷成不同圓柱”的實踐活動，探索“在圓柱側面積相等時，卷成的圓柱體積相不相等及其緣由”。教師通過把準火候的三次追問，引領學生層層遞進，不斷走向思維的更深處。

一、“進”，符號表示

問題一“卷成的兩個圓柱體積一樣大嗎”學生直接判斷有困難，計算比較勢在必行。

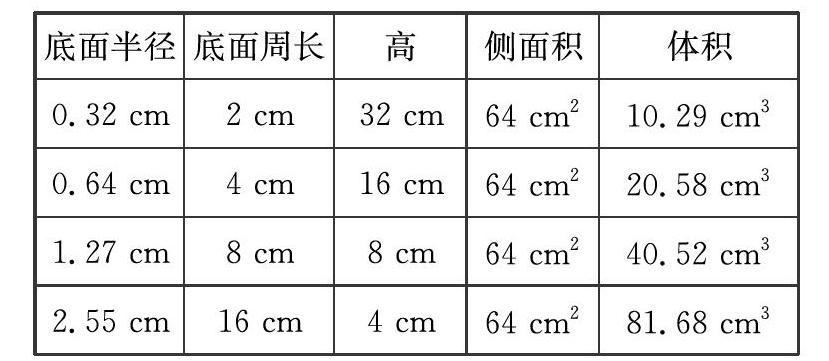
為了凸顯計算結果的價值，采取填表的匯報形式（保留2位小數）。

借助表格，學生很快發現：圓柱側面積相等時，底面積大的體積較大。

教師及時跟進：有更簡單的計算辦法嗎？

學生提出：“除以3.14和乘以3.14算起來很麻煩，直接帶著π計算試試。”

如果底面周長是16 cm，高是4 cm。

組1：圍成圓柱的底面半徑表示為：16÷2÷π=8π，

組2：底面積可以為：8π2×π=64π，

組3：圓柱體積就是：64π×4=256π。

如果底面周長是4，高是16……

學生很快得出，圍成的圓柱體積是64π，256π>64π，結論不變。

華應龍強調：學生在同一層面徘徊時，教師要及時跟進，巧妙提升。學生通過觀察產生初步的猜想后，教師適時地向前引一引：“有更簡單的計算辦法嗎？”這樣既優化了計算的過程，又為學生探索問題二做好了鋪墊。

二、“進”，有序排列

問題二既是對初步發現的規律的驗證，又是在此基礎上更深入的探索。

先請學生判斷圍成圓柱體積的大小，再計算驗證。

學生匯報計算結果時順序混亂，不便比較。

教師適時跟進：怎樣填寫，大家研究起來更方便些？

學生觀察后提出，可以按從小到大或從大到小的順序填寫。

匯總數據用表格呈現如下，翔實的數據驗證了猜想的正確性。

教師再次跟進：這兩張粘好的紙條，還能圍成別的圓柱形嗎？閉上眼睛想一想，如果能，怎樣圍成的圓柱體積最大？

生1：可以換個方向圍。

生2：第二張紙條換個方向，還是一樣，因為它是正方形。

生3：如果換個方向圍，第一張長紙條圍成的圓柱體積大。

學生再次計算填表。（表略）

教師此次跟進，與教科書上的要求不同，引領學生走進了更廣闊的思維空間。學生不僅再次經歷驗證自己猜想的過程，而且經歷從動手操作到空間想象的過程，積累了豐富的數學活動經驗。

三、“進”，抽象規律

部分同學堅持要展現另一種填表方式。（題目要求保留2位小數，他們的成果沒有機會展示）

如果帶著“π”計算，確實要簡便得多，這是筆者當時的真實想法。

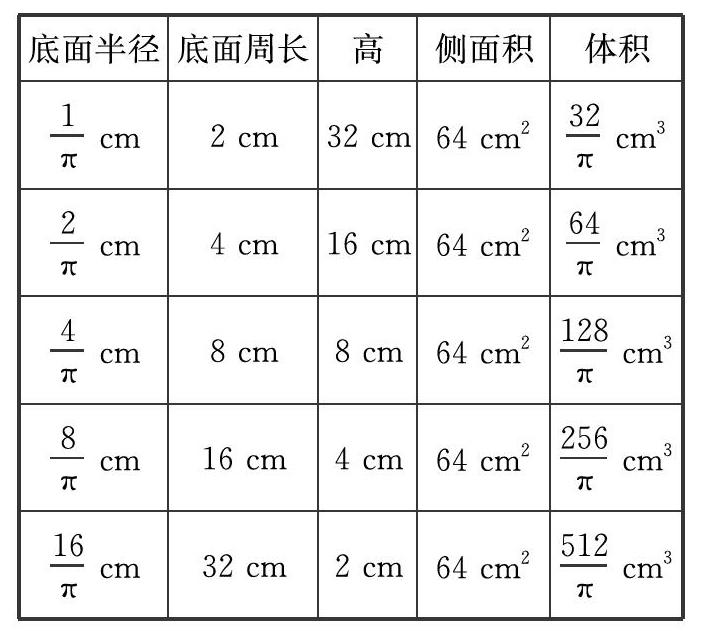
此表一出，全場震驚！

學生不僅發現了“圓柱體的側面積相等時，底面積大的體積大”，而且還發現了“圓柱的側面積相等時，底面半徑的比=體積的比”。

教師繼續追問：是不是所有的側面積相等的圓柱體，都具有這個規律呢？學生陷入深思。

組1：用字母可以表示運算律，也可以表示這個規律吧。

組2：用a、b表示長方形的長和寬（b

……

于是，同學們的新表又產生了。

學生強烈的探索欲望促使教師又進一步追問：“側面積相等的圓柱體，底面半徑的比=體積的比”具有普遍性嗎？感興趣的同學課后可以試一試……

課后反思：

一、培養學生深度思考的習慣

1.“進一步”促思考

無論是對計算結果的有序排列，還是帶著“π”參與計算，以及用字母表示發現的規律，每一個環節教師都有意識地引導學生“進”一步，促使學生深度思考。每一次“進”，都把握火候，找準節點，既立足學生的知識基礎，又溝通新舊知識間的聯系，不讓學生在舊知處徘徊，促使探索活動由課內延伸到課外。

2.“進一步”養習慣

學會思考才有發展潛力。實踐活動課不是計算練習課，要引領學生擺脫怕思考、不思考、淺思考的陋習，養成愛思考、真思考、深思考的思維習慣。恰如鄭毓信所言，“通過數學學會思維”。波利亞也指出，“知識和能力的核心是思維”。數學學習不僅要獲得知識、提高能力，更要促進思維品質的發展，養成有根據、有條理、有深度的思考習慣。

二、培養學生深度思考的策略

1.培養學生勇于探索的精神

實踐活動課的學習氛圍，讓多數學生不知不覺地參與進探索活動中。他們動腦想、動嘴說、動手測量和計算，對結果有了初步的猜想并用計算數據驗證發現，再通過集體的多次實驗得出正確的結果。在活動過程中，學生合作需求強烈，探索欲望“爆棚”，理性思維、批判質疑的火花不斷閃現，探索精神得到充分張揚。

2.培養學生深度探索的習慣

六年級的學生對探索規律的常用策略并不陌生，他們經歷了運算律、圖形面積和體積公式推導等的探索過程，積累了較為豐富的數學活動經驗。他們能依據教材提供的問題情境尋找有用信息，經歷從不同算式得到相同規律的過程，再通過舉例驗證、比較分析，完善對規律的認識。學生帶著“π”計算，為用字母表示規律做好了鋪墊，從具體的數據中跳出來，由特殊到一般，關注事物的本質屬性。養成用科學的思維方式認識事物、解決問題的習慣，數學的核心素養才能得到可持續發展。

參考文獻：

[1]林崇德《中國學生發展核心素養到思維品質的培養》（講座）

[2]余文森.核心素養導向的課堂教學[M].上海：上海教育出版社，2019.

[3]北師大版六年級數學下冊教科書，2014.