一類分數階非線性時滯系統的穩定性與鎮定

趙 冬， 李婷婷， 尹 昊

(1- 合肥工業大學管理學院，合肥 230009; 2- 淮北職業技術學院基礎部，淮北 235000;3- 合肥工業大學自動化系，合肥 230009)

1 Introduction

In recent years，fractional calculus，fractional differential equations and their applications have aroused wide attention of physicists and engineers. It has been proved to be valuable tools in the modeling of many phenomena in various fields of engineering，physics and economics. In describing the complex physical and mechanical problems of some systems， the physical meaning of the fractional model is more clearer and concise statements. Researches on theory and applications of fractional calculus have become a hot topic[1-5].

Stability analysis is one of the most fundamental and important issues for the control systems. In spite of intensive researches， the stability of fractional order systems remains a challenging problem. Much considerable attentions have been devoted to the stability analysis and control design for fractional-order linear time invariant systems[6-12]. As we all know， the world is nonlinear， linearity is only its approximate description， it is desired to investigate nonlinear systems from the theoretical and applied points of view. However， due to the difference between fractional-order differential systems and integer-order differential ones， some methods to deal with the integer-order systems such as Lyapunov direct method， can not be simply extended to fractional-order ones， the relevant researches are still in an initial stage[13-16].

Due to time-delay phenomena existing in various fields of engineering， physics and economics，nonlinear delayed systems represent a wide class of infinite-dimensional systems. And more importantly，the existence of time-delay being often a significant cause of instability and deteriorative performance. Investigating the delay effecting on stability and performance of control systems has received much attention over the past few decades. In particular， it is worth noting that the combined use of the fractional derivative and delay may lead to a better description of such systems with memory effect. To the best of our knowledge， there are few papers about the stability and stabilization of fractional-order nonlinear delayed systems. Sadati et al proved two theorems for Mittag-Leラer stability of the fractional nonlinear delayed systems[17，18]，but for fractional-order nonlinear system[19]， it is not convenient to construct a suitable Lyapunov function. Motivated by the aforementioned discussions， this paper is dedicated to obtain the stability and stabilization sufficient condition for a class of fractional-order nonlinear systems with time delay.

The remainder of this paper is organized as follows. In section 2， some necessary definitions are presented. Main results are proposed in section 3. In section 4， an example and corresponding numerical simulations are used to illustrate the validity and feasibility of the proposed method. Finally， conclusions are drawn in section 5.

2 Preliminaries and problem description

In this section， some notations， definitions and well-known results about fractional differential equations are presented firstly.

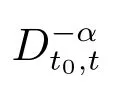
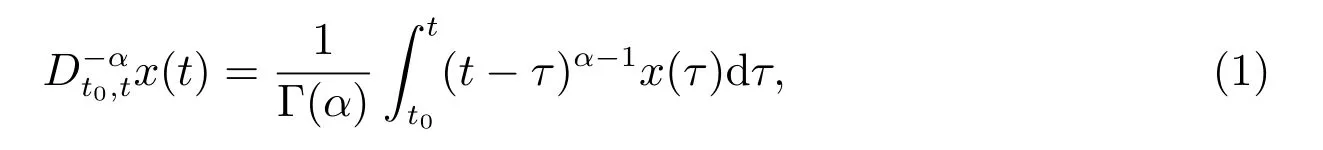
where Γ(·) is the Gamma function，

Definition 2[20]The Caputo derivative of fractional order α of function x(t) is defined as follows

where n-1 ＜α ＜n ∈Z+.

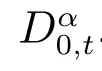
Consider the following fractional-order nonlinear delayed systems

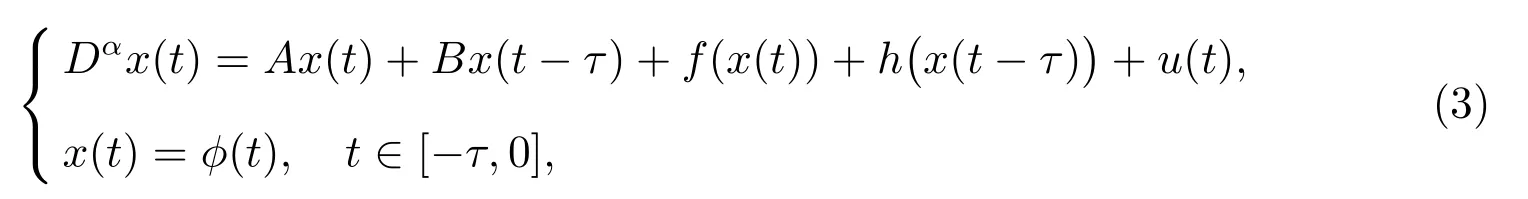
or

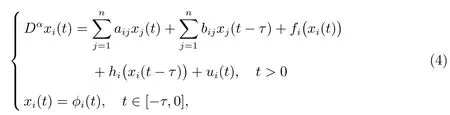
where x(t) = (x1(t)，x2(t)··· ，xn(t))T∈Rndenotes the state vector of the state system， f，h : Rn→Rndefine nonlinear vector field in the n-dimensional vector space，fractional-order α belongs to 0 ＜α ≤1，A=(aij)n×n∈Rn×nand B =(bij)n×n∈Rn×nare constant matrices，

f(x(t))=(f1(x1(t))，f2(x2(t))，··· ，fn(xn(t)))T，

h(x(t-τ))=(h1(x1(t-τ))，h2(x2(t-τ))，··· ，hn(xn(t-τ)))T，

time-delay τ ＞0. φ(t)∈C([-τ，0]，Rn) is the initial function with the norm

Let Ω = (C[0，T]，R，‖·‖)， where (C[0，T]，R) denote a class of all continuous column vector functions. For x ∈(C[0，T]，R)， the norm is defined by

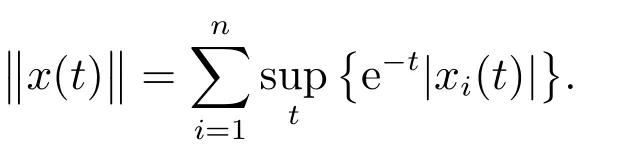
u(t) is control input which will be designed later. Here， f(·)，h(·)∈Rnare assumed to satisfy

3 Main results

In this section， some sufficient conditions are presented for the stability and stabilization of a class of fractional-order nonlinear delayed systems， respectively.

Theorem 1The fractional-order nonlinear delayed system (3) with u(t) = 0 is stable if ‖A*‖+F +‖B*‖+H ＜1 holds， where

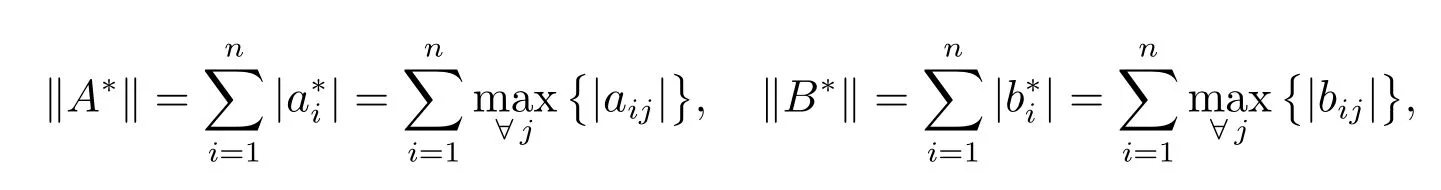
F =max{Fi}， H =max{Hi}.

ProofThe solution of the system (4) can be expressed in the following form

Then， one obtains

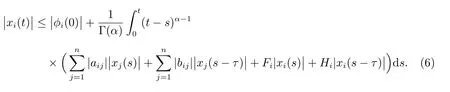
By multiplying e-ton both sides of (6)， one has

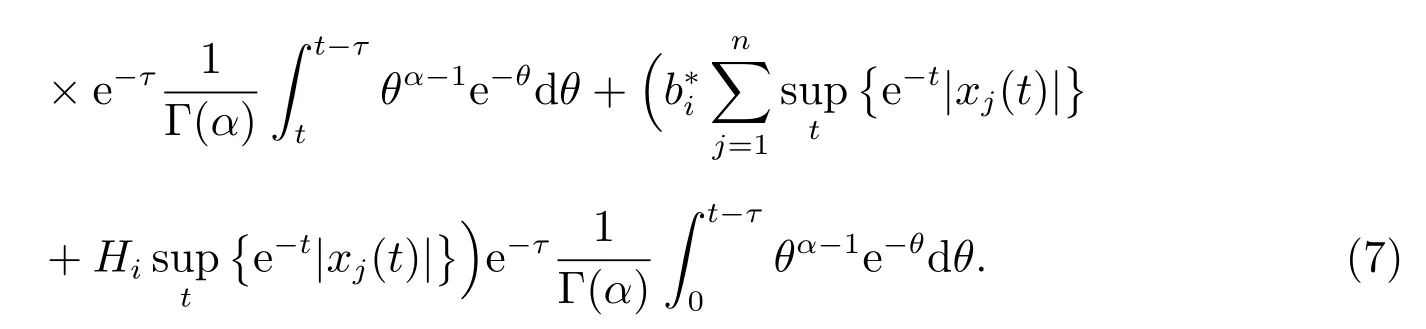
From (7)， one can get

From (8)， one has

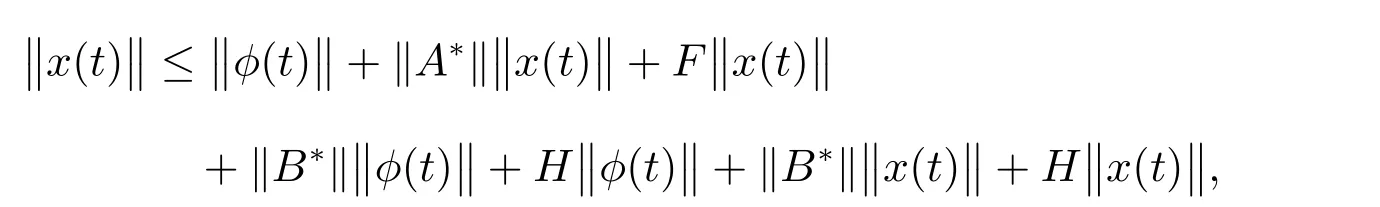
i.e.，

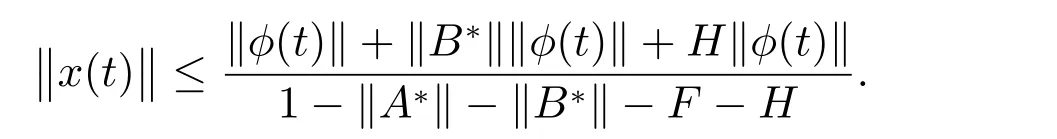
Therefore， for all ε ＞0， there exists

such that ‖x(t)‖＜ε when ‖φ(t)‖＜δ， which means that the solution x(t) is stable.

Obviously， the following corollaries hold from the Theorem 1.

Corollary 1The fractional-order nonlinear delayed system (3) with u(t) =-K1x(t) - K2x(t - τ) is stable if feedback gain K1and K2satisfy ‖(A - K1)*‖ +F +‖(B-K2)*‖+H ＜1.

Corollary 2The fractional-order nonlinear delayed system (3) with u(t) =-K1x(t) is stable if feedback gain K1satisfies ‖(A-K1)*‖+F +‖B*‖+H ＜1.

Corollary 3The fractional-order nonlinear delayed system (3) with u(t) =-K2x(t-τ) is stable if feedback gain K2satisfies ‖A*‖+F +‖(B-K2)*‖+H ＜1.

4 Numerical example

In this section，to verify and demonstrate the effectiveness of the proposed method，we apply them to stabilize a fractional order delayed nonlinear system. Consider the following 2-dimensional fractional-order delayed nonlinear system

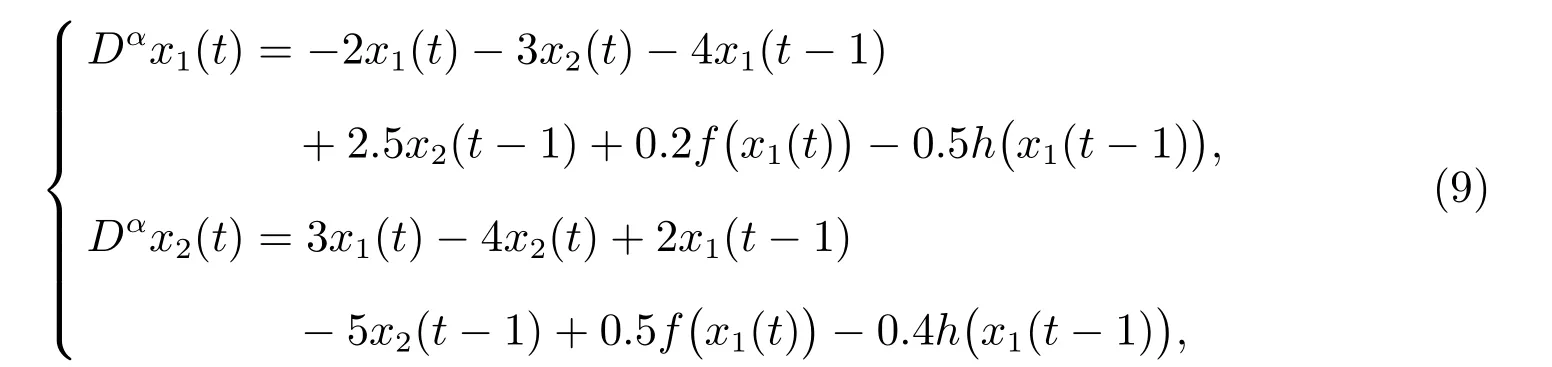
where α=0.8， f(x(t))=tanh(x(t))， h(x(t))=0.5(|x+1|-|x-1|)， system (9) can be rewritten as system (3)， where

Figure 1 shows the time evolution of state of system (9) without control input. According to Corollary 1， we chose feedback gain

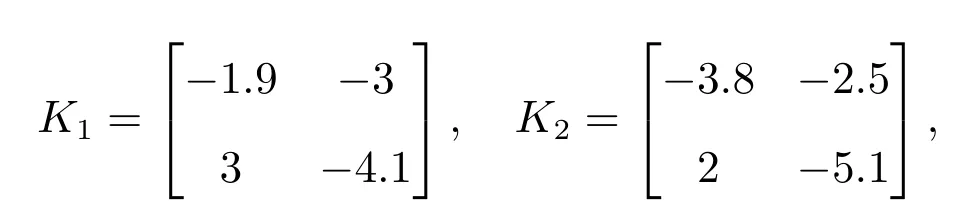
which satisfies the conditions

‖A-K1‖+F +‖B-K2‖+H =0.3+0.1+0.2+0.2=0.8 ＜1.

Figure 2 displays that the zero solution of the controlled system is stable.

Figure 1 The state trajectory of system (9) without control input

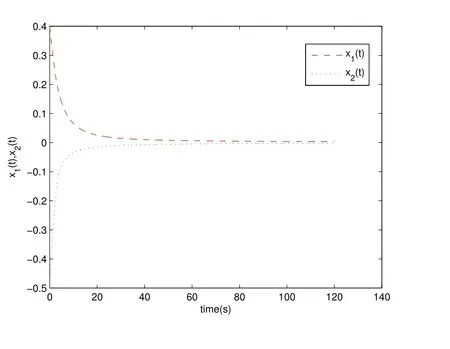
Figure 2 The state trajectory of system(9) with control input

5 Conclusion

In this paper， two sufficient conditions on stability and stabilization for a class of fractional-order nonlinear delayed systems are given， respectively. A simply numerical simulation example illustrates the effectiveness of the developed methods.