面向對象多粒度概念格的構造

李克文， 呂萌萌， 邵明文

(中國石油大學(華東)計算機與通信工程學院，青島 266580)

1 引言

德國Wille 教授于1982 年提出形式概念分析理論(Formal Concept Analysis， 簡記為FCA)[1]，用于形式概念(外延(對象的集合)和內涵(屬性的集合)組成的二元組)的發現、排序和顯示，其核心數據結構是概念格結構模型.概念格是知識表現的一種模型，依據知識在內涵和外延上的依賴或因果關系建立概念層次結構，生動簡潔地體現了概念之間的泛化和特化關系[2-4].形式概念分析是數據分析和知識處理有力的形式化工具，目前已成功應用于數據挖掘[5-7]、軟件工程[8]等領域.

粒計算[9，10]起源于人工智能、粗糙集、商空間、概念格、模糊集等領域，通過構造和處理信息粒度，將復雜問題劃分為一系列更容易處理的、更小的子問題，從而降低全局計算代價，進而從更高層次上對結果進行綜合分析.Zadeh[11]于1979 年首次提出模糊信息粒后，在模糊集的基礎上提出了粒計算的基本框架并強調粒度及其在推理中的重要性.近年來，粒計算已廣泛應用于數據挖掘、模式識別與智能控制、復雜問題求解等諸多領域[12-16]，及當下較為前沿的研究熱點，如時空、空間研究領域[17-19].

目前，已有許多專家學者對粒計算及相關領域進行了系統的研究，Yao[20-24]討論了粒度的綜合水平和粒計算理論.作為粒計算的模型之一，粗糙集理論[25]通過屬性集合對論域進行目標概念的刻畫，進行屬性約簡[26]、規則提取[27]與問題決策[28]等.Qian 等[29]基于多個粒結構提出了多粒度粗糙集模型，推廣了粒計算的單粒度粗糙集模型，有助于獲得信息系統的最滿意決策或問題求解，充分體現了粒計算方法的豐富性和靈活性.Gu 等[30]研究了多粒度標記信息系統中的知識近似問題.Wu 和Leung[31]對多粒度決策表中的粒度標記塊理論和應用進行了研究.基于多粒度標記信息系統對最優粒度的選擇在文獻[31-37]中進行了研究.基于多粒度粗糙集模型，Xu 等[38]研究了廣義多粒度粗糙集以及最優粒度的選擇問題.由此可知，粒計算領域的研究熱點已經由單粒度問題過渡到更具有現實意義的多粒度問題.

概念格和粒計算的方法論在本質上具有相似之處，兩種理論的結合研究已經引起了眾多學者的關注.Du 等[39]對概念格與粒度劃分的相關性進行了研究，分析了概念格與論域中的劃分關系在概念描述與概念層次之間轉換的關系.Belohlavek 和Sklenar[40]對形式概念格中的屬性粒度進行研究.Kang 和Miao[41]對基于概念庫的形式概念格屬性粒度進行了分析，結合形式概念格的結構信息，在處理屬性粒度時提出了上下確界，并提出了基于屬性粒度的形式概念格擴展模型.張清華等[42]給出了概念知識粒與概念信息粒的相互轉化方法.隨后，Belohlavek 等[43]提出了屬性粒度樹，對屬性粒度的粗細進行研究，同時提出了控制經典概念格中概念數量的Zoom 算法以實現多粒度經典概念格的快速構造，從而豐富了形式概念格中屬性粒度的研究.Zou 等[44]提出了快速提升形式概念格屬性粒度的“展開算法”.Wang 等[45]的研究內容從粒度優化問題過渡到多粒度聯合求解的問題.

假設用戶想用概念格的方法來分析商品的銷售情況，可以用商品名稱、商品銷售的時間(上午、下午)、地域(東部、西部)、商品銷售區域人們的收入水平(高于5000 元、低于5000 元)等描述商品的屬性表示商品銷售.屬性粒度太大，描述對象太模糊，用戶只得到很少的概念，無法提取有用的知識.類似地，若選擇太小的屬性粒度，可能會產生冗余概念，增大提取知識的成本.因此，通過不斷改變屬性的粒度得到不同的概念格，進而發現數據中潛在、有趣的知識自然成為一種迫切的需要.

綜前所述，對概念格中的屬性粒度進行研究具有重要意義.然而，當前只有經典概念格中的屬性粒度變換研究，因此本文提出面向對象多粒度概念格的構造算法-Zoom，從而實現具有不同屬性粒度組合的面向對象概念格的快速構造，同時附上實例演示幫助讀者理解算法.

2 相關知識

2.1 形式背景和面向對象概念生成算子

定義1[46]記三元組(G，M，I)是形式背景，其中G 是非空的對象集合，M 是非空的屬性集合，I 表示G 和M 之間的二元關系(I 是(G×M)的子集).

形式背景一般用二維表表示，行表示對象，列表示屬性，行列交叉處的取值表示屬性與對象的隸屬關系，1 表示對象具有屬性，0 表示對象不具有屬性.

如表1 所示，對象的全集是{x1，x2，x3，x4，x5，x6}，屬性的全集是{a，b，c，d，e}.第一行數據表示對象x1具有屬性{a，c，d，e}，第一列數據表示屬性a 由對象{x1，x2，x5，x6}所具有.

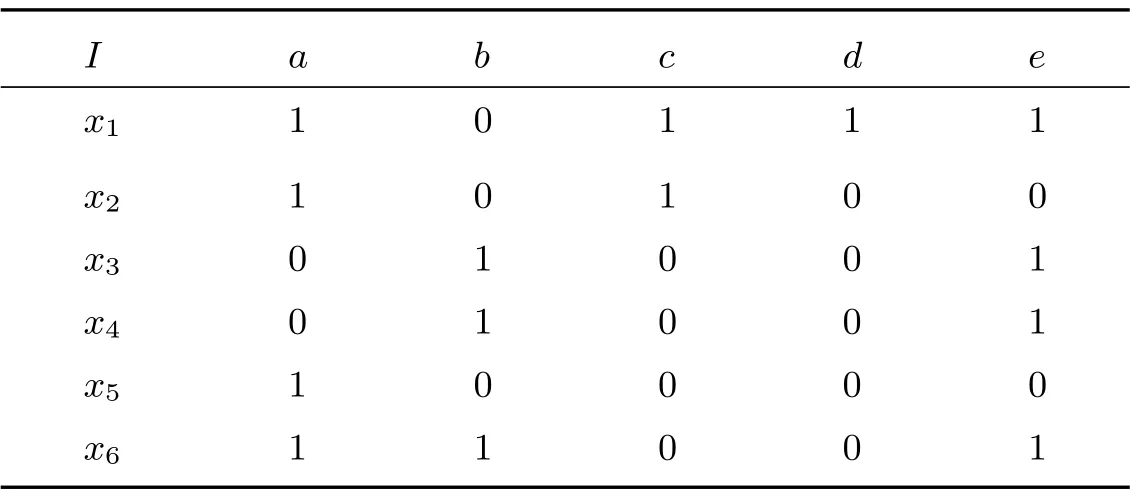
表1 形式背景(G，M，I)

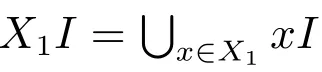
定義2[46]設(G，M，I)為形式背景，X ?G， B ?M，定義面向對象概念生成算子(↑，↓)，如下所示.

2G→2M：

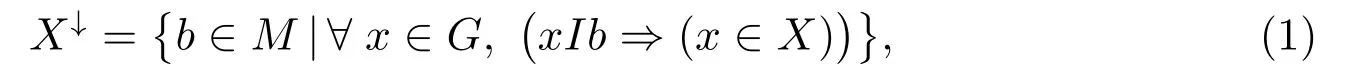
其中X↓表示只由X 中的對象擁有的屬性組成的屬性集合.

2M→2G：

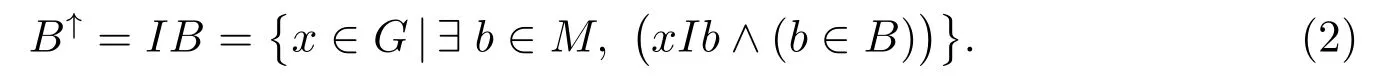
設X1，X2?G，算子(↑，↓)具有以下性質[46]：

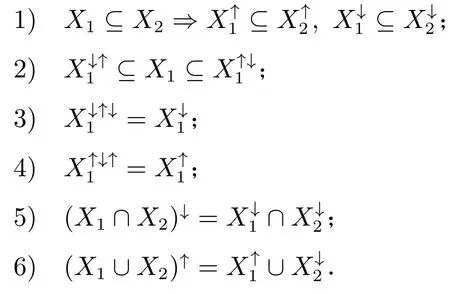
2.2 面向對象概念格

本小節介紹面向對象概念格的相關概念.

定義3[46]設(G，M，I)為形式背景，若對于任意的(X，B)， X ?G， B ?M， X =B↑， B =X↓，則稱二元組(X，B)為面向對象概念.

設C1= (X1，B1)， C2= (X2，B2)是兩個面向對象概念，如果X1?X2(B1?B2)，則記(X1，B1) ≤(X2，B2).若?C0= (X0，B0)，使得(X1，B1) ≤(X0，B0) ≤(X2，B2)，則稱(X1，B1)是(X2，B2)的直接子概念，(X2，B2)是(X1，B1)的直接父概念，形式概念之間的這種關系稱為概念之間的偏序關系用“≤”表示.

定義4[46]設(X1，B1)， (X2，B2)為面向對象概念，面向對象概念間的交(∧)、并(∨)運算如下

由表1 所示的形式背景，得到如圖1 所示的面向對象概念(格節點)及概念格.其中，概念的外延為對象(此處用形式背景中對象的右下數字表示)集合，內涵為屬性(此處用字母表示)集合.

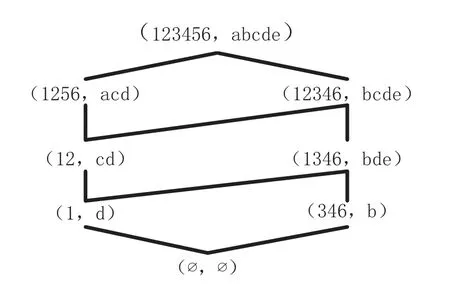
圖1 面向對象概念格

2.3 屬性粒度

在計算機領域，粒度是指保存數據的細化或綜合程度.在不同屬性粒度的轉換過程中，發現最優粒度是粒計算的一個重要應用.屬性粒度越小，描述對象越細致.例如，一個屬性“Grade”([0-100] points)可以細分到另一個屬性粒度的級別：{“Fail”([0-60)points)，“Pass”([60-100]points)}，繼續細分到下一個屬性粒度的級別：{“Worse”([0-30) points)，“Bad”([30-60) points)，“Good”([60-90) points)，“Good”([90-100] points)}.

下面引入粒度樹及相關定義.

定義5[43]用一個樹根為Z 的樹形結構表示屬性Z 的粒度等級，稱具有以下特點的樹形結構為屬性Z 的粒度樹：

1) 樹根是粒度最大的屬性Z，樹的每一個節點都有一個獨一無二的標簽Zi；

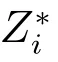
3) 如果{z1，z2，··· ，zi，zi+1，··· ，zn}是粒度大小相同的粒子的全集(粒度樹的一個粒層)，且滿足以下三個條件，則稱{z1，z2，··· ，zi，zi+1，··· ，zn}是Zi的一個劃分：

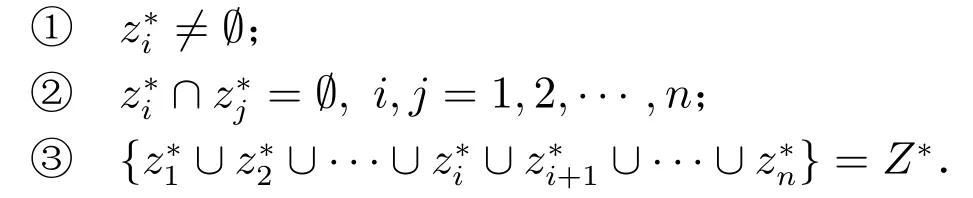
如圖2 所示，屬性成績的粒度樹共有3 個粒層，分別是：{{Grade}， {Pass， Fail}，{Worse， Bad， Good， Excellent}}.

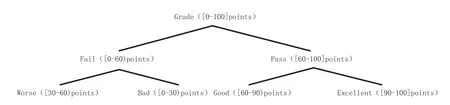
圖2 “Good”的粒度樹

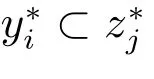
設(G，M，I)為形式背景，

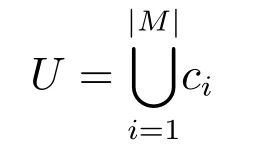
表示由每個屬性的一個粒層組合在一起形成的粒層集合，其中ci表示第i 個屬性的粒度層級，|M|表示(G，M，I)中屬性的個數.

同一形式背景中屬性的不同粒層集合之間存在一種偏序關系，設

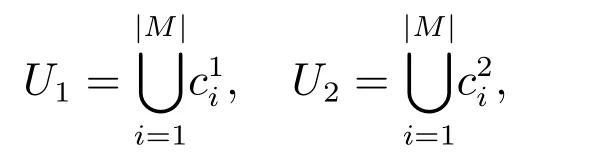
基于屬性不同的粒層組合可以得到不同的形式背景(G，MU，IU)，設U1={L，R，G}， U2={L，R，{lG，dG}}，由此得到如表2 所示的兩個形式背景(G，MU1，IU1)(左)、(G，MU2，IU2)(右).其中{G}， {lG，dG}是屬性“Green”的粒度樹的兩個粒層，且{lG，dG}≤{G}.

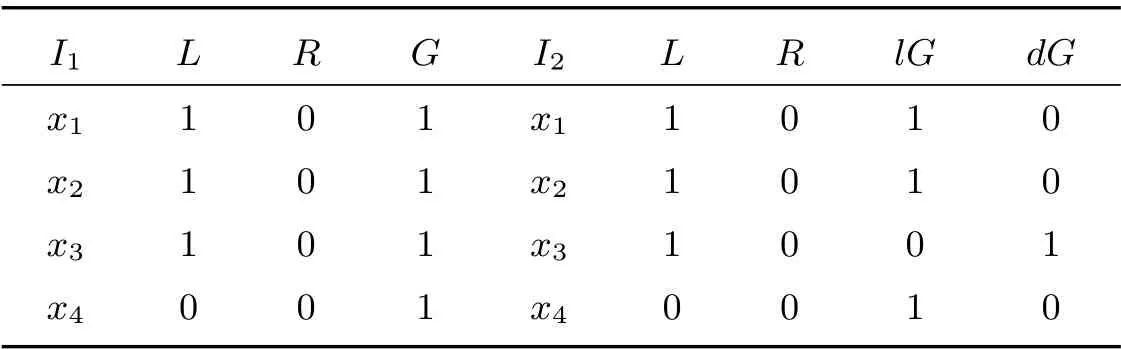
表2 形式背景(G，M，I)

3 面向對象多粒度概念格的構造算法—Zoom

屬性粒度改變前后，概念格中的概念存在內在聯系，為了方便研究概念格變化的規律，現作以下定義：

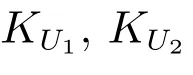
3.1 面向對象多粒度概念格的屬性粒度細化算法-Zoom-in

3.2 面向對象多粒度概念格的屬性粒度粗化算法-Zoom-out

由此，Zoom-out 的正確性得證.

以上是針對面向對象概念提出的Zoom 算法，通過類似于面向對象概念的相關定理易于得到面向屬性概念的相關定理及面向屬性概念格的Zoom 算法.在經典的概念格構造算法中，消耗時間最多的步驟是每層概念兩兩運算得到新概念，設每層概念的個數為N，則經典概念格的構造算法時間復雜度為O(N2)，而Zoom 算法是在原有概念格的基礎上對每個概念格的內涵與外延單獨進行計算，所以時間復雜度為O(N)，因此，與經典概念格的構造算法相比，Zoom 算法的時間復雜度較低，因此執行效率更高，有助于在實際應用中從數據中進行知識的挖掘.

4 結語

屬性粒度對于從數據中提取概念進而得到概念格的結構有重要影響，選擇合適的屬性粒度水平進行組合，可以有效的控制概念格中概念的數量，進而有助于用戶發現有趣的知識.對于屬性粒度水平的選擇依賴于領域專家的經驗知識.通過分析概念內涵、外延在屬性粒度變化前后的關系，對原概念格的概念進行分類，在此基礎上，我們提出的算法-Zoom 可以在已有概念格和粒度樹的基礎上直接實現面向對象概念格的構造，避免了利用傳統概念格構造算法從形式背景生成概念繼而得到概念格的繁重工作量，從而提高了概念格的構造效率.下一步，我們將研究面向屬性多粒度概念格的構造以及面向對象多粒度概念格、面向屬性多粒度概念格、經典概念格之間的轉換關系，后續將研究多粒度廣義單邊概念格的快速構造算法.