基于徑向基函數的自適應網格方法

段獻葆， 黨 妍， 秦 玲

(西安理工大學理學院，西安 710048)

1 引言

許多物理和工程實際問題都可以用偏微分方程來描述，但是只有極少數的偏微分方程可以得到精確解，所以對于一般的偏微分方程，都是借助于數值方法求解.比較成熟的數值方法中大部分是依賴于網格的，如有限差分法、有限元法、有限體積等等.這些方法必須先生成網格后才能求解，網格質量的好壞直接決定了最終數值求解的精度，而網格生成的預處理耗費時間太大，在求解區域不規則或維數較高時，這些方法都有一定的困難.另一方面，在應用這些方法求解大變形、斷裂問題或高維問題，特別是非定常問題，很多時候在求解的過程中都需要網格重構，這大大地增加了計算量，也嚴重降低了數值解的精度[1，2].為了解決這些問題，自適應網格方法是一個很好的選擇，國內外許多學者在這方面進行了大量地研究[3-6].

同樣是為了解決有限元方法等對網格依賴的問題，無網格方法近年來受到了很大的關注[7，8].這類方法試圖徹底地或部分地消除網格.相對于網格依賴的數值方法，無網格方法具有一些明顯的優點，因此在其出現后得到了日益眾多的關注，并且一直是偏微分方程數值方法中的一個研究熱點.一般說來，無網格方法基于一系列節點進行函數插值，與有限元等網格依賴的方法相比，避免了網格劃分的預處理過程，也不會出現網格畸變的問題，對間斷問題、解的變化較大的問題等具有較好的優勢.另一方面，無網格方法只需各個節點的獨立信息，而不需要單元之間的相互信息，數據結構簡單.

利用徑向基函數(Radial Basis Function， RBF)求解偏微分方程的方法，是最近幾十年來備受關注的一類無網格方法[9].近年來，人們已經用RBF 方法求解了各種線性和非線性的偏微分方程，并且取得了不錯的結果.其基本思想是在求解區域內根據所求解的問題布置節點，然后在每個節點上構造RBF，再將RBF 代入到所求解的偏微分方程，通過求解最終得到的代數方程獲得近似解.與網格依賴的方法不同，RBF 方法不需要任何網格，對支撐域和邊界沒有要求，只需要以節點為中心的子域覆蓋所求解區域即可.同時，RBF 與空間維數無關，僅依賴于節點間的距離，低維結果可以很容易推廣到高維問題.事實上，RBF 是通過定義在[0，+∞)上的一元函數φ 與Rd上的歐幾里德范數‖·‖來表示d 元函數φ(‖x-y‖)，其中x，y ∈Rd.因此用RBF 來處理多元問題具有效率高、儲存方便、運算簡單的特點.RBF 已廣泛應用于計算幾何、微分方程數值解、神經網絡等領域.近年來，國內外學者對RBF 的理論與應用進行了系統的研究，隨著RBF 理論的逐漸發展，目前已成為求解偏微分方程的一個強有力的工具[10-15].但是RBF 方法的缺點也是顯而易見的，如理論方面很不完善，在逼近過程中所得到矩陣方程的系數矩陣是否可逆沒有相關理論結果，也即數值解的唯一性還沒解決；隨著中心節點增加，需要求解一個很大的方程組，并且這個方程組經常是病態的；尚未見到開源或商業化的軟件，后處理以及所得結果與其他軟件的接口比較困難等等.為了解決這些問題，已經有學者考慮自適應的RBF 方法[16，17]，以及把有限元方法和RBF 方法相耦合的方法[18].

為了發揮無網格方法和網格依賴方法各自的優勢，我們提出了一種基于徑向基函數的自適應網格方法.利用有限元方法等數值結果結合徑向基函數方法在求解區域內進行自適應配點，克服了有限元等方法計算中網格畸變和重新生成帶來的困難，所得結果可以用有限元等方法的后處理技術進行分析.數值結果說明，所提方法產生的網格可以根據解的變化情況進行網格自適應，從而在保證相同數值求解精度的情況下可以極大地節省計算量.

2 徑向基函數

徑向基函數插值方法以其計算格式簡單、節點配置靈活、精度高的特點而成為研究多元逼近理論的有利工具，并已經被應用于科學計算模擬和實際工程問題中.

徑向函數滿足以下條件[19]：如果‖x1‖ = ‖x2‖，就有φ(x1) = φ(x2)的函數φ，也即，僅依賴r = ‖x‖的函數(其中‖·‖為Euclid 范數).RBF 就是這樣的函數空間：給定一個在定義域x ∈Rd上的一元函數φ:R+→R，所有形如Φ(x-c)=φ(‖x-c‖)及其線性組合張成的函數空間稱為由函數φ 導出的RBF 空間.在一定的條件下，只要取{xj}兩兩不同，{Φ(x-xj)}就是線性無關的從而形成徑向基函數空間中某子空間的一組基.當{xj}幾乎充滿R 時，{Φ(x-xj)}及其線性組合可以逼近幾乎任何函數[9].

1) Kriging 方法的Gauss 分布函數(無限光滑)：φ(r)=exp(-βr2)， β ＞0.

2) Duchon 的thin plate(薄板)樣條函數(分片光滑)：

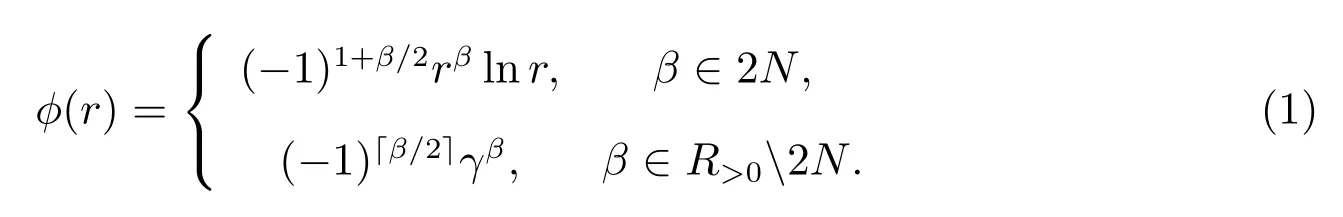
3) Sobolev 樣條函數：φ(r)=Kβ-d/2(r)rβ-d/2，其中K 為MacDonald 函數.

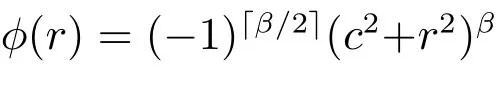
用RBF 求解偏微分方程的一般步驟如下：

對于偏微分方程

其中L 是偏微分算子，B 是邊界算子.在Ω 內配置N 個離散的數據點r1，r2，··· ，rN，其中r1，r2，··· ，rl是內部節點，而rl+1，rl+2，··· ，rN是邊界節點.設方程(2)的解u 可以用RBF 表示為

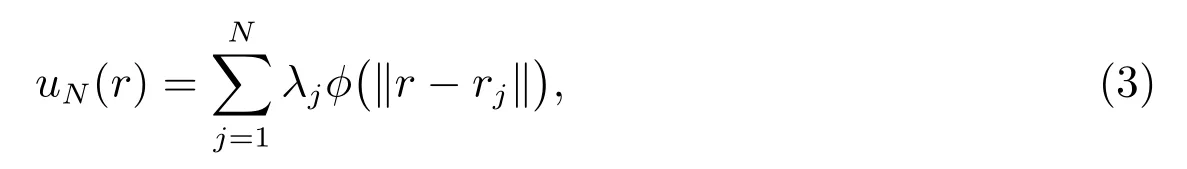
其中λ1，λ2，··· ，λN為待定系數.由(2)式和(3)式可得

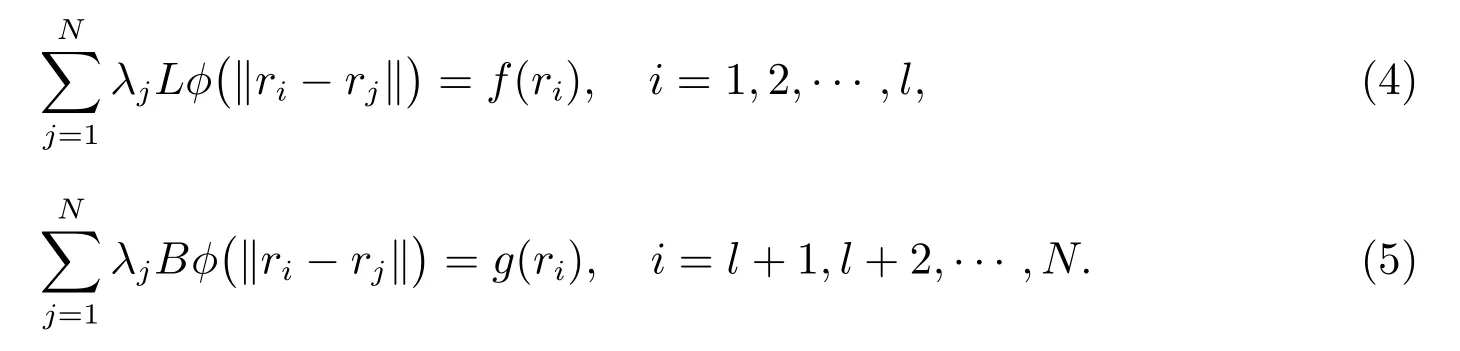
由(4)和(5)兩式得到矩陣方程

其中

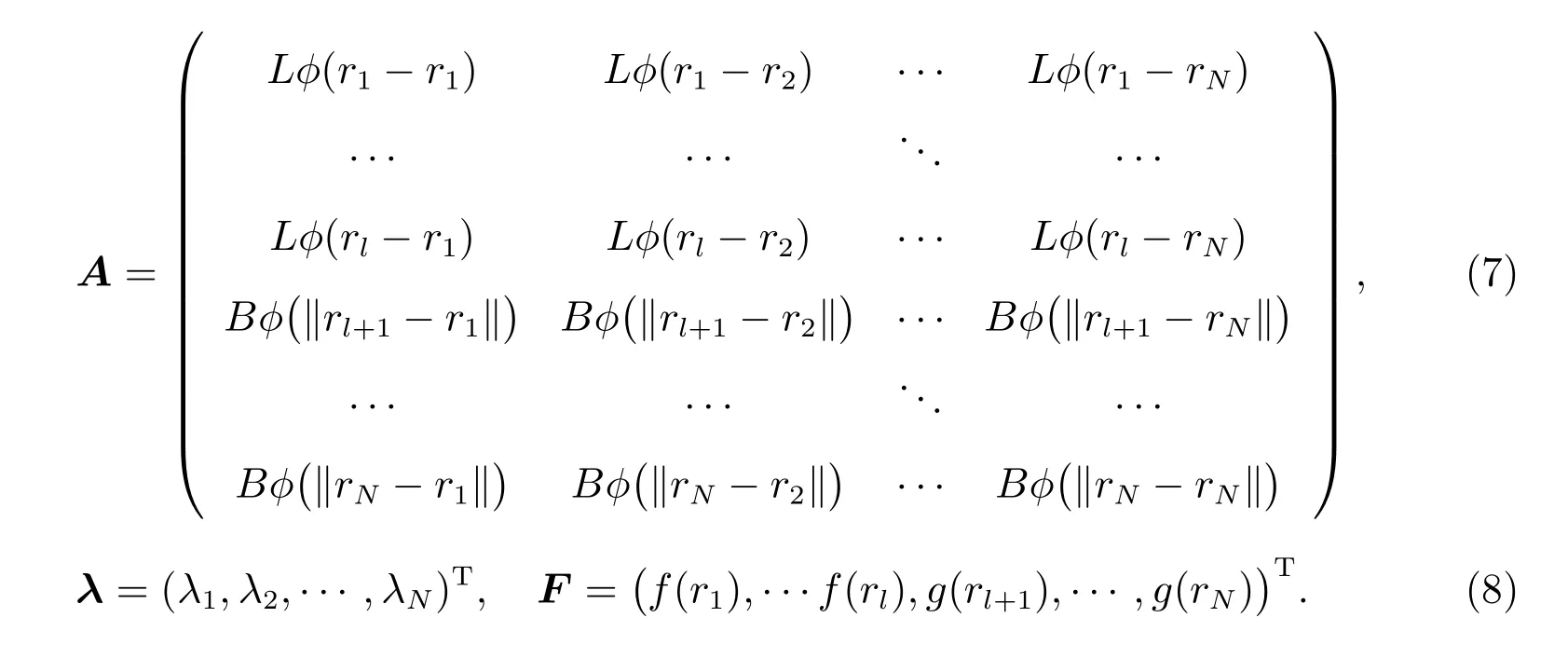
若矩陣A 是非奇異的，矩陣方程有唯一解，只要從(6)中解出λ，就可以得到方程(2)的近似解uN.

3 自適應網格方法

最早由Berger 和Oliger 于1984 年提出的自適應網格方法[20]，是一種高效且準確的數值方法.該方法拋棄了等距均勻的網格，代之以能夠自動地適應所研究問題中解的特征的疏密程度不均的網格.其網格結構隨著計算過程的推進而不斷的動態改變，根據計算的實際需要以及問題的特性改變計算區域內的網格結構，在物理量變化比較劇烈的地方，例如：大變形、激波面、接觸間斷面和滑移面等，采用空間尺度較小的精細網格，在物理量變化緩慢的地方則采用空間尺度較大的粗網格，這樣在保持計算高效率的同時得到高精度的數值解.

這一節我們給出一種簡單、易于實現的自適應網格方法.該方法基于插值來調整RBF 的中心和參數，從而改變RBF 節點的分布.

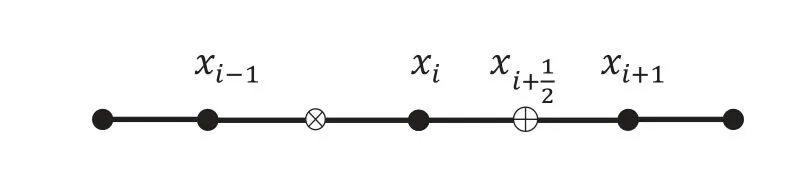
圖1 網格自適應過程

對于二維問題來說，首先將求解區域進行有限元分割，然后進行有限元求解，與一維問題類似，用所得到的數值解可以求出方程(3)中的系數λi；接下來，可以用徑向基和λi得到每個初始單元的中點(重心)處的值，用這個值與有限元解在這點的插值得到誤差；誤差超過給定閾值的點將成為新的節點，并且利用這個節點把所在的單元進行剖分；同樣，若誤差低于給定閾值，所在單元的節點都將被移除.

注1由于RBF 方法隨著節點的增加計算量會顯著上升，在誤差大于給定閾值的單元可以多細化幾次，但也不需要細化太多次.從我們的計算結果來看，細化兩次就可以達到非常理想的效果.

注2同一個節點可能會同時作為細化和粗化單元的節點，我們是先進行細化，然后進行粗化.

注3另一種可以采用的方法是一次增加多個節點，但在這個過程中會增加計算量，特別是RBF 方法.

注4這里給出的自適應過程非常容易實施，并且可以推廣到更高的維度.

對于某些偏微分方程問題來說，如果初始節點不是太多，上述過程還可以簡化.如對于如下具有齊次Dirichlet 邊值的Poisson 問題

方程組(6)變為

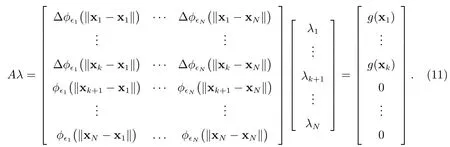
可以用RBF 方法直接求得系數λi.此時可以用如下公式

得到在節點{y1，y2，...，yM}處的誤差，其中M 為RBF 的節點數.

4 數值算例

本算例考慮Burgers 方程的求解問題.Burgers 方程是偏微分方程中的一個非常重要的方程，廣泛應用于各個領域，如流體力學、非線性、氣體動力學、交通流等等.由于Burgers 方程是一個非線性方程，只有在很少的一些特殊情況下可以得到精確解，在更一般情形下，連數值求解都存在很大的困難.

我們考慮如下非定常Burgers 方程

其中Ω ?R2，?Ω 是Ω 的邊界，u =(u1，u2)是流體的速度.ν =1/Re(Re-Reynolds 數)是粘性系數，f 表示體積力，g 為已知函數.

設V =H1(Ω)2，則(13)-(15)的弱形式為：求u ∈V，使得

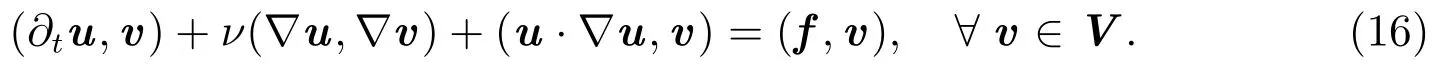
設Th是Ω 的一個三角剖分(h 是剖分參數)，Vh是有限元空間，Vh?V，則(16)的有限元解為：求uh∈Vh，使得

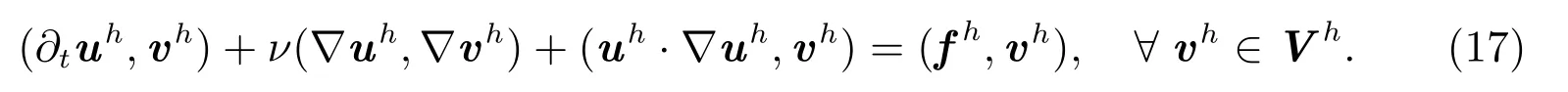
在下面的計算中，求解區域Ω=[0，1]×[0，1]， T =1，時間步長為Δt=0.01，

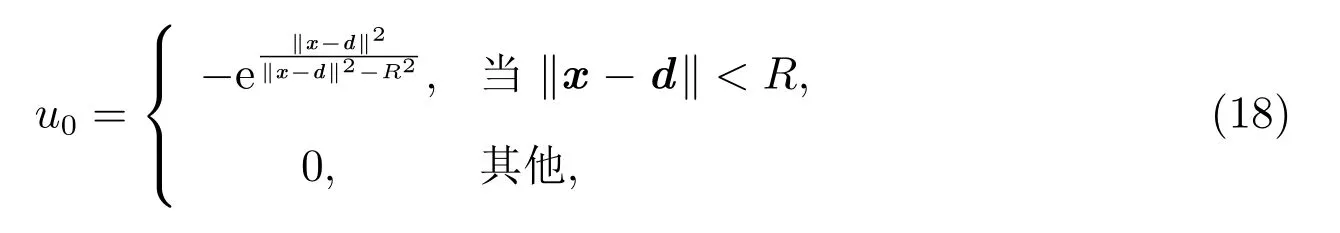
其中‖·‖表示歐氏范數，x =(x1，x2)， d =(0.3，0.3)， R=0.25.

本算例求解的過程中，當誤差大于2×10-3時進行網格細化，小于2×10-6時進行網格粗化.粘性系數ν = 0.01.圖2 至圖4 分別給出了問題在時間t = 0， 0.5， 1 時的解.其中，圖2(a)、圖3(a)、圖4(a)為RBF 節點分布；圖2(b)、圖3(b)、圖4(b)為節點對應的有限元網格；圖2(c)、圖3(c)、圖4(c)為網格對應的有限元解.其中為了看得清楚，有限元解的圖片旋轉了一個角度.

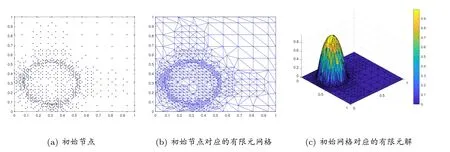
圖2 t=0 時的解

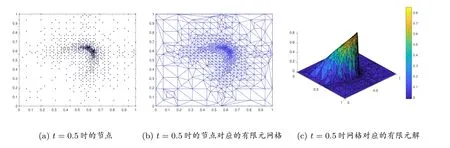
圖3 t=0.5 時的解

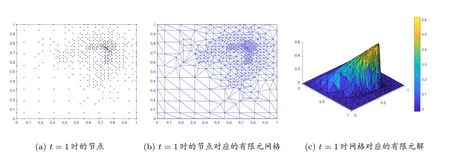
圖4 t=1 時的解

利用本文所提算法，在t = 0.5 時所用節點數和有限元網格單元數分別為656 個和1286 個，所用時間375.8368 秒.作為比較，我們用傳統有限元方法在t=0.5 時對本問題進行了求解，所得結果如圖5 所示：用相同節點數的均勻(粗)網格對Burgers 方程進行了求解，所得結果如圖5(a)所示，可以看出所得結果非常粗糙，根本無法接受；用均勻加密(細)網格可以得到與圖3(c)接近精度的解，如圖5(b)所示，采用節點和有限元網格單元數分別為2704 個和5202 個，所用時間1184.7050 秒，大約是本文所提算法的3.15 倍.

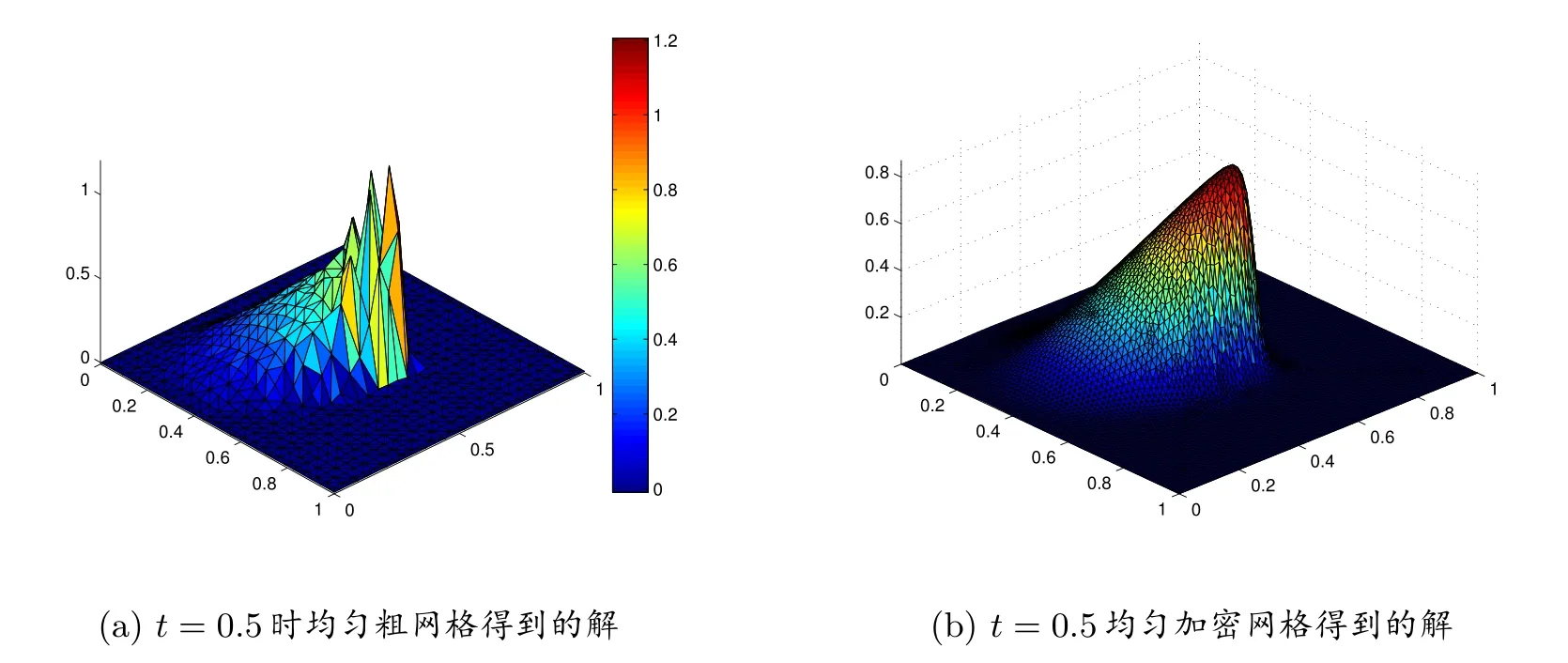
圖5 傳統有限元方法得到的解

從以上算例可以看出，本文所提算法可以在保持網格數量減少或不變的前提下較好的提高問題的求解精度，從而節省了求解時間.

5 結論

本文給出了一種求解偏微分方程的自適應網格方法，該方法把徑向基函數計算格式簡單、節點配置靈活的優點與網格依賴方法的穩健性很好地結合起來.該算法非常容易實施.數值算例也表明所提算法可以在解變化劇烈的區域加密網格，而在解變化平緩的地方粗化網格，從而可以保持較高精度的前提下減少或不增加計算量.我們用非定常Burgers 問題對算法進行的驗證說明所提算法可以高效地求解偏微分方程問題.