基于狀態觀測的非脆弱跟蹤控制器設計

程權成，崔寶影

（遼寧機電職業技術學院 華孚儀表學院，遼寧 丹東 118009）

0 引 言

在控制系統分析中，穩定性分析和跟蹤性能分析是兩類典型的分析方法，跟蹤性能分析比穩定性分析更加復雜。跟蹤控制是指通過設計控制器，在保證系統穩定的前提下，使系統的輸出變量能夠跟蹤某一參考信號的輸出變量。由于在控制器的設計過程中，并不是所有的狀態變量都是可直接測量的，因此本文采用狀態觀測方法對狀態變量進行觀測，進而完成控制器的設計。劉玲等為了保證被控系統的跟蹤控制性能，提出一種基于狀態反饋的H∞跟蹤控制器設計方法[1]；鹿竹葉等以火電機組機爐協調系統為研究對象，對閉環系統進行H2/H∞跟蹤性能分析，并給出求解的LMI條件[2]，二者均假定狀態變量是直接可測量的，但在實際系統模型中該假定并不是永遠成立的。吳海東等結合LMI技術和魯棒理論，研究了智能車軌跡跟蹤控制方法提高了跟蹤精度和魯棒性，該研究分析了系統模型中的不確定性，但對于控制器的脆弱性沒有進行深入探討[3]。石振東等主要針對四旋翼無人機系統模型，研究了一種基于Lyapunov穩定性理論的H∞跟蹤控制器[4]；孫宜標等采用LMI方法對直線伺服系統進行位移跟蹤控制，并設計了求解控制器的條件[5]，二者均未考慮控制器中存在擾動時對跟蹤性能的影響。Lin Chong等針對T-S模糊系統設計了基于觀測器的跟蹤控制器，應用LMI技術給出跟蹤控制器的求解條件，并通過質量彈簧機械系統驗證了設計方法的有效性，但其應用于線性連續時間系統時，求解過程過于復雜[6]。已有研究都是假定跟蹤控制器是精確執行的，即未考慮非脆弱問題，然而，在實際系統模型中，由于A/D轉換精度、元器件老化等因素，控制器參數往往并不是準確執行的，控制器參數微小的變化都會給系統帶來嚴重的影響。本文利用非脆弱控制理論進行跟蹤控制器求解條件的推導，即考慮跟蹤控制器內部中存在的擾動，利用Lyapunov函數方法和LMI方法，設計跟蹤控制器和觀測器的存在條件，所研究的跟蹤控制器及觀測器綜合采用H∞理論以及非脆弱理論，并通過數值仿真證明所提出方法可有效實現系統的跟蹤性能和穩定性。

1 問題描述

考慮連續時間系統模型（1），將針對該系統模型進行基于狀態觀測器的跟蹤控制器的設計。

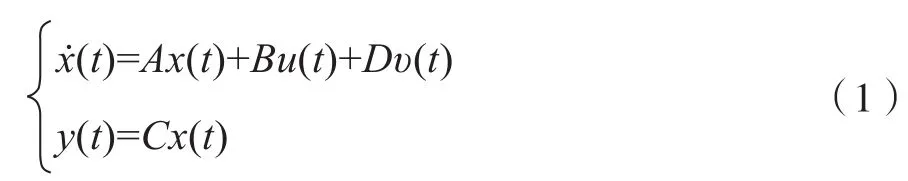
考慮參考模型如（2）所示，本文的控制目標是設計跟蹤控制器使得y(t)能夠跟蹤yr(t)[6-8]。

實現跟蹤控制目標的同時需要滿足（3）所示的H∞輸出跟蹤控制性能指標[6-8]：

其中，χ(t)=y(t)-yr(t)，δ(t)=[υT(t)rT(t)]T，Q為正定的加權矩陣，γ為給定的性能衰減指標。

為實現該系統的跟蹤控制問題，選取基于觀測器的跟蹤控制器模型為：

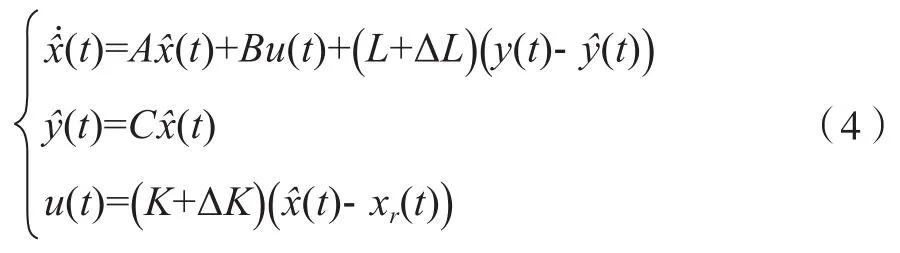
構建變量?(t)=[κT(t)xT(t)xT r(t)]T和κ(t)=x(t)-(t)，結合（1）、 （2）和（4），可構建閉環系統模型（5）：

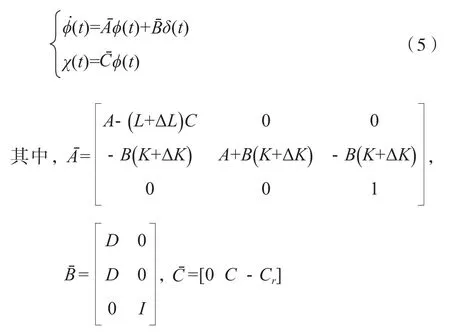
設計的主要任務是求解計算非脆弱H∞跟蹤控制器K及觀測器L，使（5）滿足當δ(t)=0時是穩定的，同時存在γ＞0，使得性能指標（3）成立。

引理1和引理2將在本文結論的推導過程中起到重要作用。

引理1[9-11]：對于矩陣不等式條件（6）和不等式條件（7）是等價的。

引理2[12]：對于給定適當維數的實矩陣X=XT,H,E, ΔTΔ≤I，可以得出結論，存在任意的常數λ＞0，使其滿足下面的不等式關系：

2 非脆弱跟蹤器設計

利用LMI技術，推導非脆弱H∞跟蹤控制器的LMI條件，該條件可通過Matlab軟件求解。

定理1 針對閉環系統模型（5），若存在矩陣G1,J,F,G3,H以及常數ε1＞0,ε2＞0和γ＞0使得（9）成立：

證明：Lyapunov函數

由于G＞0，可知ρ(0)=0，且ρ(∞)＞0，因此， （11）成立。

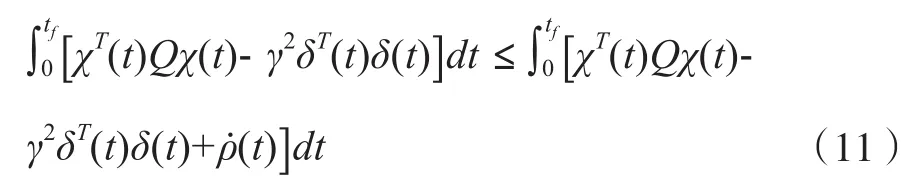
因此，如果（12）成立，那么閉環系統模型（5）的H∞跟蹤性能就能保證。

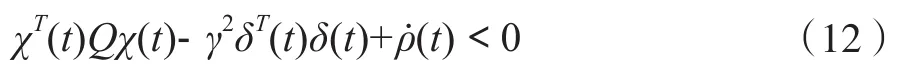
將χ(t)和δ(t)的定義代入（12），可得：

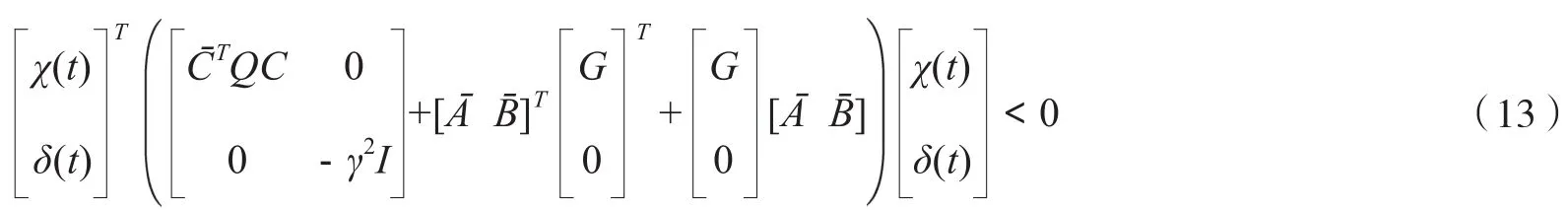
如果（14）成立，那么（13）成立。

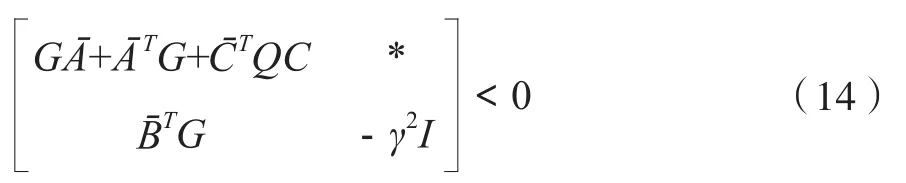
將引理1應用于（14），可得（15）。

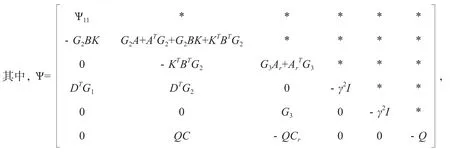
3 仿真實例

為進一步證明所設計基于觀測器的H∞非脆弱跟蹤控制器設計方法的有效性，設計仿真實例進行驗證。選擇系統的系數陣和外部干擾υ(t)如下：

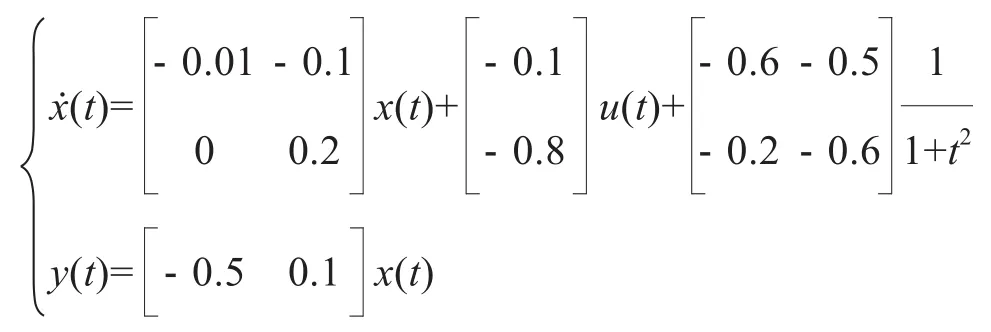
假定參考模型參數如下：

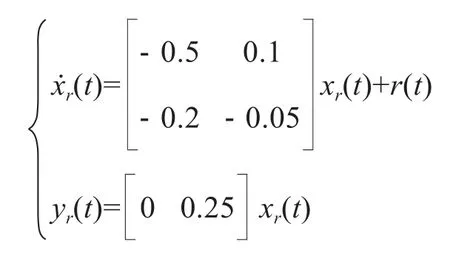
使用Matlab軟件的M文件編寫定理中闡述的非脆弱H∞跟蹤控制器的LMI程序，當γ2=2.1時，求解出的跟蹤控制器增益參數為：

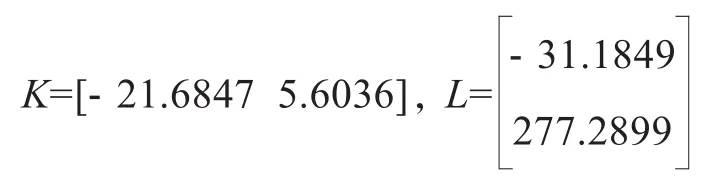
仿真過程中假設觀測器和跟蹤控制器中的參數增益不是精確可執行的，存在擾動的形式為ΔK=[0.1 0.2]*cos(t)*0.6和ΔL=[-0.7 0.01]*cos(t)*0.03。參考輸入信號r(t)選擇兩種形式，形式1為：

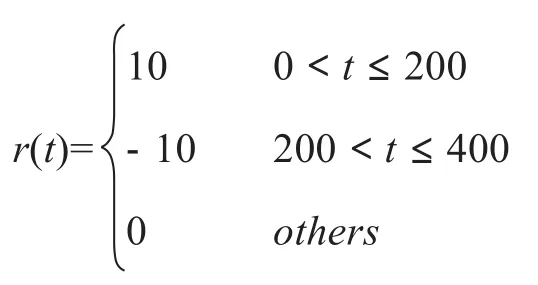
形式2為：r(t)=10+sin(0.05t)

對兩種形式分別進行仿真。

使用Matlab軟件的Simulink仿真功能進行基于觀測器的非脆弱H∞跟蹤控制器的穩定性和跟蹤性能的分析，針對兩種不同的參考輸入信號r(t)，可仿真出閉環系統（5）的輸出狀態y(t)和參考模型輸出變量yr(t)變化曲線如圖1和圖2所示。可見，所設計的跟蹤控制器和觀測器在存在內部擾動的情況下仍然能夠實現對參考信號的跟蹤，且當r(t)=0時，閉環系統（5）的輸出狀態y(t)也為0。因此，閉環系統（5）同時滿足了跟蹤控制性能和穩定性能，所設計的控制器是有效的。

若不進行非脆弱控制理論進行分析，則當跟蹤控制器和狀態觀測器中存在干擾ΔK和ΔL時，針對兩種不同的參考輸入信號r(t)，閉環系統（5）的輸出狀態y(t)和參考模型輸出變量yr(t)變化曲線如圖3和圖4所示。可見，不進行非脆弱設計，則存在干擾ΔK和ΔL時，雖然也可以實現信號的跟蹤，但跟蹤性能不及圖1所示狀態優越，尤其當參考輸入信號r(t)為形式2時，y(t)與yr(t)的幅值與相位偏差均很嚴重。

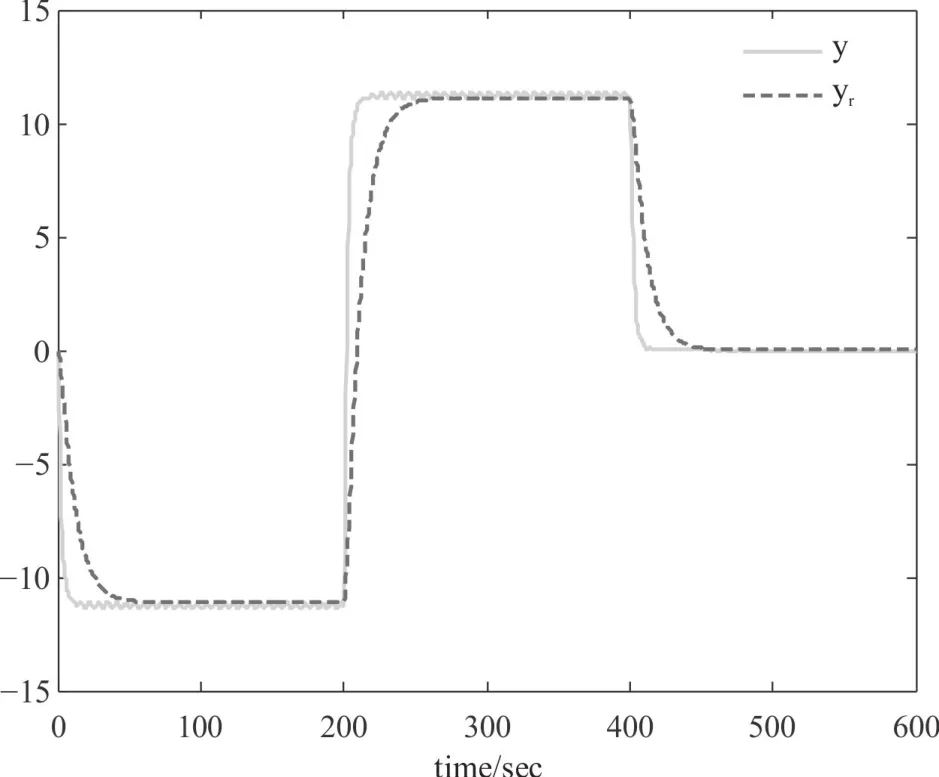
圖1 閉環系統輸出y(t)和參考模型輸出yr(t)響應曲線（r(t)為形式1）

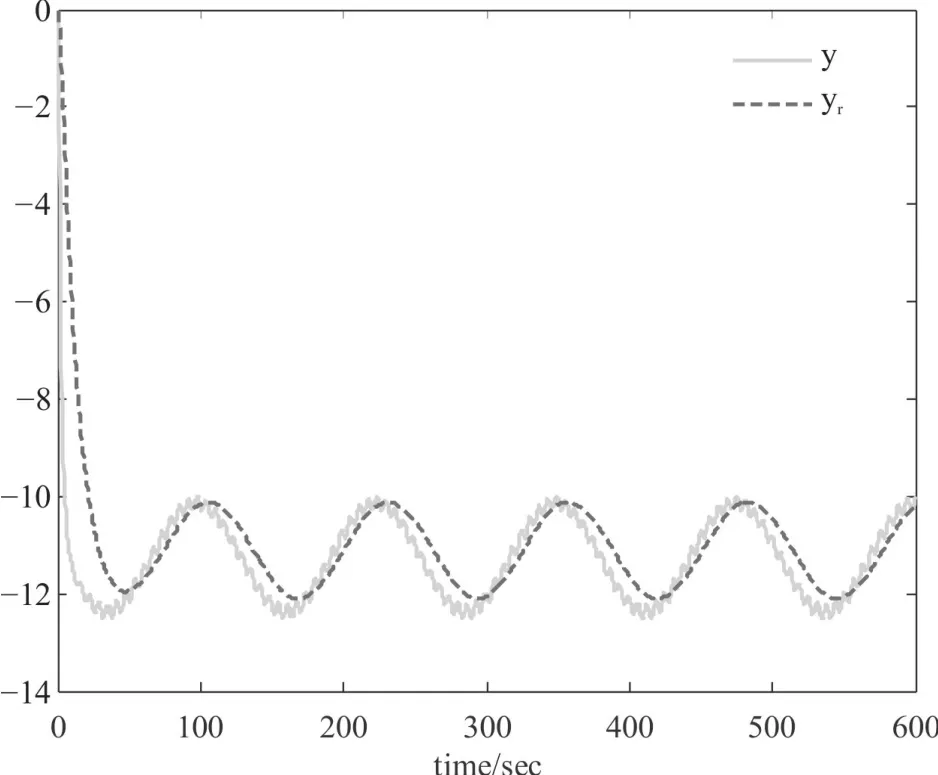
圖2 閉環系統輸出y(t)和參考模型輸出yr(t)響應曲線（r(t)為形式2）

圖3 未進行非脆弱設計的閉環系統輸出y(t)和參考模型輸出yr(t)響應曲線（r(t)為形式1）

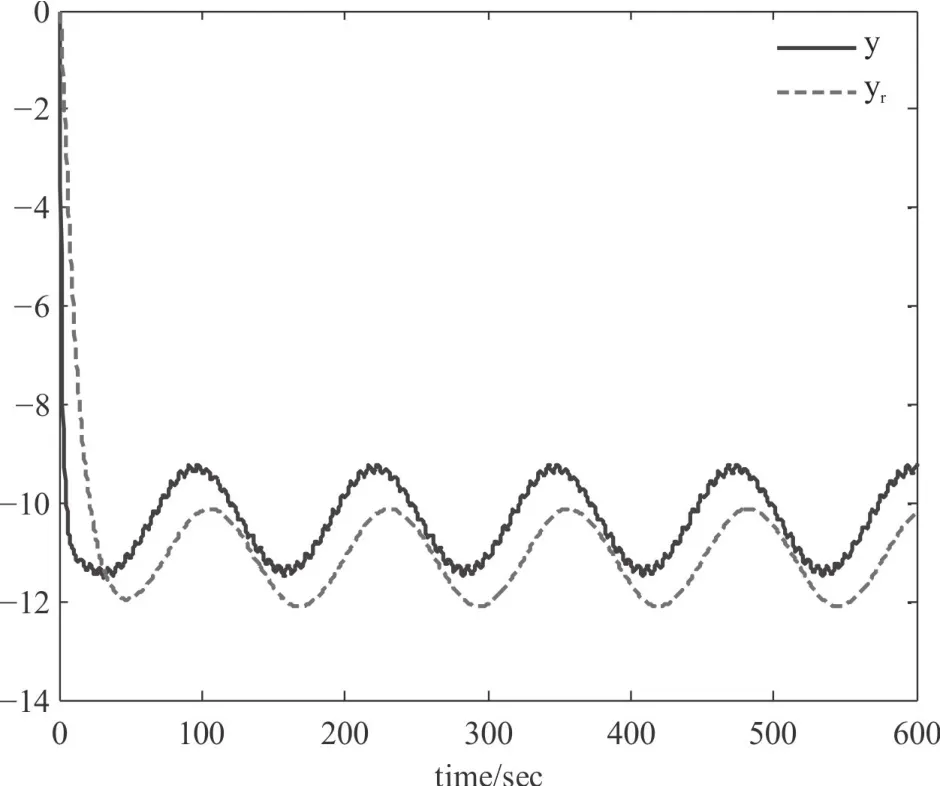
圖4 未進行非脆弱設計的閉環系統輸出y(t)和參考模型輸出yr(t)響應曲線（r(t)為形式2）

針對兩種不同的參考輸入信號r(t)，跟蹤誤差響應曲線如圖5和圖6所示，e1為進行非脆弱設計時的跟蹤誤差響應，e2為未進行非脆弱設計時的跟蹤誤差響應，可見在任何時刻e1均比e2更趨近于0，即非脆弱設計后的跟蹤誤差小于傳統控制器的跟蹤誤差。因此，可以得出結論，進行非脆弱設計后的跟蹤控制系統，其跟蹤控制性能比傳統控制器系統更加優越。

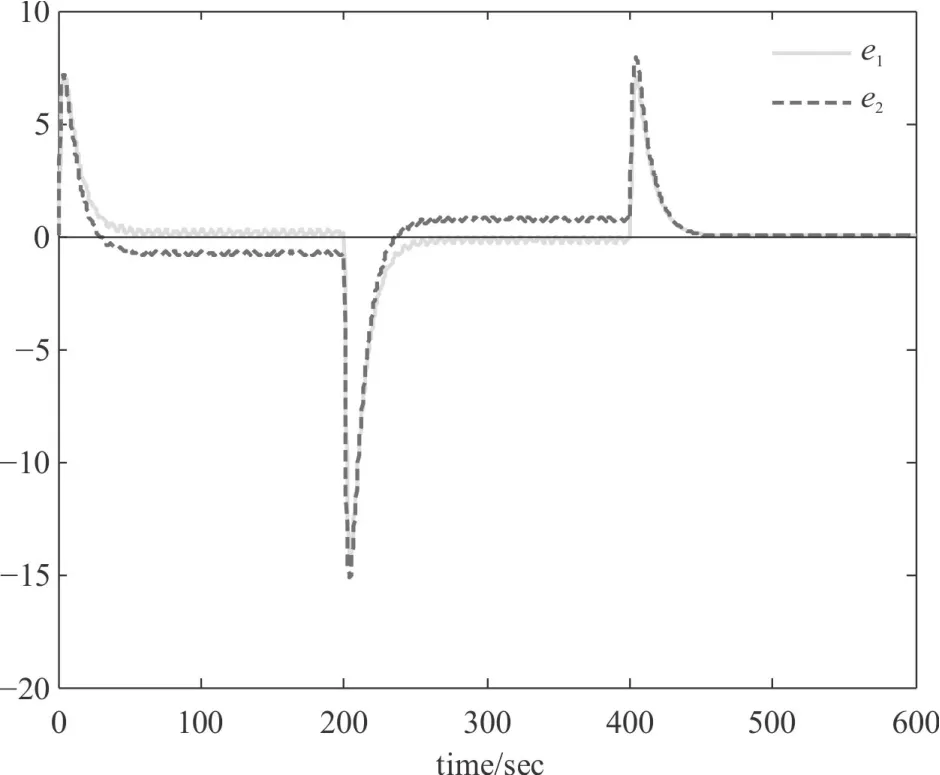
圖5 跟蹤誤差響應曲線（r(t)為形式1）

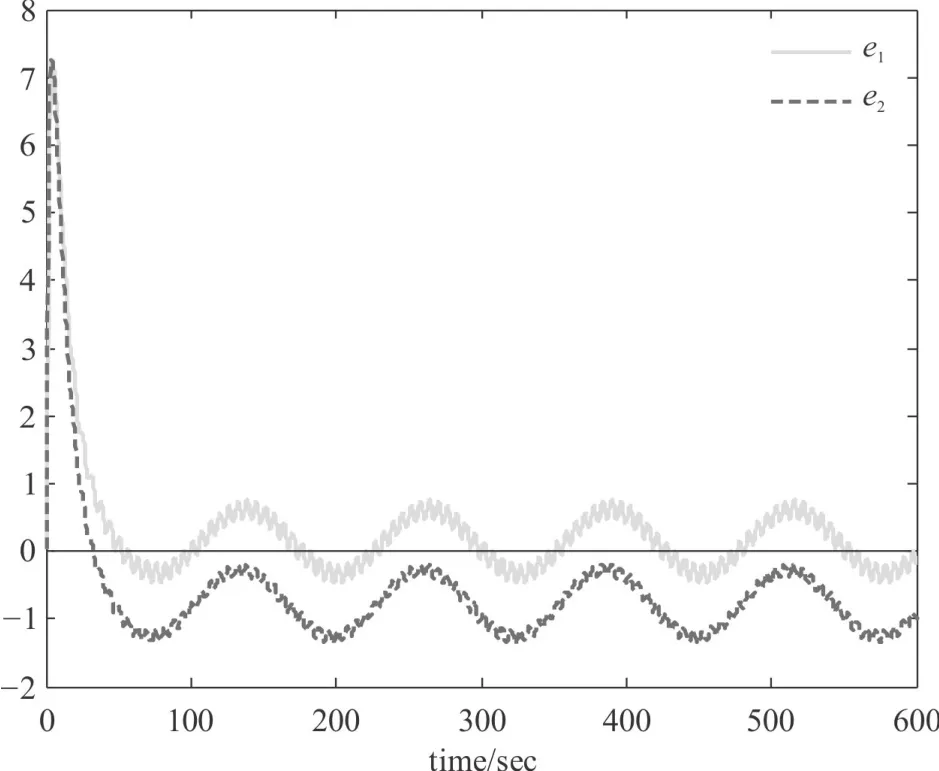
圖6 跟蹤誤差響應曲線（r(t)為形式2）

4 結 論

本文構建了一種針對連續時間系統的非脆弱狀態觀測H∞跟蹤控制器求解方法，采用Lyapunov穩定性理論方法，推導實現跟蹤控制性能的不等式存在條件，通過有效的不等式變換技術得到了跟蹤控制器的LMI存在條件。該條件可通過Matlab軟件中的LMI Toolbox工具包計算求解。利用Simulink仿真技術對所設計的閉環系統進行仿真分析，根據輸出響應曲線可以得出結論：即使當觀測器和跟蹤控制器中均存在干擾時仍然能實現輸出狀態的跟蹤性能，且當跟蹤參考信號輸入為零時，系統的輸出收斂于零，因此同時保證了跟蹤性和穩定性。研究將非脆弱設計理論引入到跟蹤控制器的應用中，增強了理論的應用性。