一種雙線性分段二分網格搜索SVM 最優參數方法?

施皓晨 肖海鵬 周建江

（南京航空航天大學電子信息工程學院 南京 211106）

1 引言

支持向量機（Support Vector Machine，SVM）采用結構風險最小化原則，根據有限訓練樣本信息，在模型的學習能力和復雜性之間尋求最佳折衷［1］，以獲得良好的推廣性能和較好的分類精確性。其核心思想是通過引入核函數，將在輸入空間的線性不可分樣本映射到高維特征空間，達到線性可分或近似線性可分［2］。

SVM 參數選擇將直接影響分類器性能的優劣。目前，參數選擇還只能憑借經驗、實驗進行搜索尋優，因此，如何選擇最佳參數已成為研究SVM的一個重要分支［3］。常用的SVM 模型參數優選方法有雙線性法［4］，網格搜索法及其改進算法［5］，雙線性網格搜索法［6］等。雙線性法是通過分析以RBF核的SVM 的漸近行為，指出學習精度高的核參數和懲罰因子組合(C，γ)集中出現在“好區”中的直線logγ=logC?-logC，由此提出了一種雙線性搜索最佳參數方法。它的優點是訓練量小，缺點是對線性SVM 最佳參數C 的準確性依賴度很大。網格搜索法則是將C 和γ分別取M 和N 個值，對M×N個(C，γ)組合分別進行訓練計算其正確率，選取M×N 個組合中正確率最高的作為SVM 模型的最佳參數。網格搜索法及其改進算法學習精度比較高，但是訓練量很大。雙線性網格搜索法結合了雙線性法訓練量小和網格搜索法學習精度高的優點，先利用雙線性法得到最佳參數，然后再用網格搜索法在最佳參數附近進行網格搜索，獲取SVM 模型的最佳參數。

在雙線性網格搜索法基礎上，利用分段二分思想（Segmented Dichotomy，SD），本文提出了一種快速尋優的雙線性分段二分網格搜索法，在搜索段間分段地采用二分法，迭代求解出每段SVM 的最高正確率，已得到所對應的最佳參數；最后，找出所有最佳搜索段的SVM 最高正確率的最大值，其對應的最佳參數即為SVM模型的最終優化參數。

2 SVM模型最佳參數(C，γ)優化方案

2.1 RBF核參數對分類器的影響

SVM 模型有兩個非常重要的參數：懲罰因子C與核參數γ。其中，懲罰因子是對誤差的寬容度。核參數是SVM 選擇RBF 函數作為核后，該函數自帶的一個參數。

懲罰因子C 可在確定的特征子空間中調節分類器置信范圍和經驗風險的比例，以使分類器的推廣能力達到最好［9］。它的選取一般由具體問題而定，不同特征子空間中最優化的C 不同。在確定的特征子空間中，C 值小表示對經驗誤差的懲罰小，分類器的復雜度小而經驗風險值較大；C 取無窮大時則所有的約束條件都必須滿足，這意味著訓練樣本必須要準確地分類。

懲罰因子C對SVM 性能的影響反映在：當C較小時錯誤率比較高；當C 增加時錯誤率急劇降低；繼續增大C 時錯誤率的變化不明顯，且當C 增加到一定值后，錯誤率不再變化。這就意味著，懲罰因子C 越高，越不能容忍出現誤差，容易過擬合。C越小，容易欠擬合。C 過大或過小，SVM 分類的泛化能力變差。進而，SVM的復雜度達到特征子空間允許的最大值，所以，在這個區域中就可以通過核參數γ的變化來得到SVM的最優推廣能力。

表4報告了城鄉居民不同收入分位點下的斷點回歸結果。可以發現，擴招政策對城鄉內部不同收入群體的影響差別顯著。其中，城鎮內部居民50%以下低收入組的教育收益率為5.4%，50%以上高收入組的教育收益率為4.1%，即擴招政策促使城鎮內部教育收益率變動趨勢趨同，但會使城鎮內部高低收入群體的收入和教育出現分化，進而形成“馬太效應”。同時，高校擴招政策會使農村內部居民不同收入群體的教育產生分化，對收入及教育回報率的影響為正但不顯著。

通常情況下，在使用RBF 核來建立SVM 模型時，參數C 和γ的選擇并沒有一定的先驗知識，必須做某種類型的模型進行參數搜索，使得分類器能正確地預測未知數據（即測試集數據）。采用交叉驗證方法來提高預測精度是一種常用的做法。k折交叉驗證是將訓練數據集合分成k 個大小相同的子集。其中一個子集用于測試，其余k-1 個子集用于對分類器進行訓練。這樣，整個訓練集中的每一個子集被預測一次，交叉驗證的正確率是k 次正確分類數據百分比的平均值［8］。它可以防止過擬合的問題，具有一定的合理推廣能力。

2.2 雙線性分段二分網格搜索方法

本文所提出的SVM 模型參數優化性能將主要受到以下三個參數的影響：1）取樣間隔值；2）C 的迭代精度；3）正確率迭代精度。在VC++和Matlab平臺上，選用標準的UCI 數據庫［7］中的Glass 數據集，采用控制變量法，從學習精度和訓練量兩方面分析這三個參數對算法可靠性的影響。實驗結果如圖1～4所示。

1）利用分段二分法搜索出線性SVM 最佳參數；

線性SVM 最佳參數［11］的準確性直接影響雙線性法和雙線性網格搜索法的學習精度，而搜索最佳參數過程中的訓練量也直接影響算法的整體訓練量，所以線性SVM 最佳參數的求解在學習精度和訓練量兩方面都對基于RBF 核的支持向量機最佳參數的選擇起著決定性影響。

用傳統二分法［12］搜索線性SVM 最佳參數時，設定C 的初始搜索范圍，然后將搜索范圍的中間值代入線性SVM 中計算錯誤率，反復迭代，達到預定的精度范圍則停止搜索。但是由于錯誤率隨C 的增大只是在整體上呈現降低的趨勢，并不是隨著C的增大而絕對單調遞減。因此，簡單的傳統二分法很容易使得最佳參數的求解陷入局部最大值。

考慮到C 對錯誤率的影響特點，將利用分段的二分法來快速精確搜索線性SVM 最佳參數。首先，在C 的初始搜索范圍內，每隔固定取樣值求出線性SVM 的交叉驗證正確率。由于錯誤率隨著C的增大在整體上呈現降低的趨勢，線性SVM 的最佳參數應該在最低錯誤率對應的C 值附近。而且，當固定取樣值取值較小時，在這個固定取樣值范圍內錯誤率隨著C 的增大絕對單調遞減。所以，在最低錯誤率（即最高交叉驗證正確率）對應的C 值附近，采用分段二分法搜索技術來尋找SVM 模型的最佳參數。具體步驟如下：

γ隱含地決定了數據映射到新的特征空間后的分布，γ越大，支持向量越少，γ值越小，支持向量越多。支持向量的個數又將影響訓練與預測的速度。核參數γ的改變，實際上改變映射函數從而改變樣本數據子空間分布的復雜程度，即線性分類面的最大VC 維［8］，也就線性決定了線性分類面能達到的最小經驗誤差［10］。核參數γ對SVM 性能的影響表現在：γ在特定的范圍內存在最小錯誤率。所以，通過對參數組合(C，γ) 的變化，可以得到SVM的最優性能。

1）對C 的初始搜索范圍進行采樣。設定C 的初始搜索范圍和取樣間隔值。在初始搜索范圍內以取樣間隔值對C 取樣，形成若干個取樣點，分別在這些取樣點上計算線性SVM 的正確率。對于不同數據集，C的初始搜索范圍和取樣間隔值可變。

2）尋找滿足一定條件的最高正確率對應的懲罰因子C。設定正確率迭代精度。找到1）中的最高正確率，在所有正確率中尋找與最高正確率的絕對差值小于正確率迭代精度的正確率，保存這些正確率及最高正確率對應的C 值。對于不同數據集，正確率迭代精度的取值可變。

3）形成用于搜索線性SVM 最佳參數的搜索段。將2）中C值中的最小值減去取樣間隔值，記為Cmin ；將C 值中的最大值加上取樣間隔值，記為Cmax 。這樣C 的初始搜索范圍就被縮小為Cmin，2）中的C值和Cmax 之間的若干搜索段。

4）二分法搜索各搜索段的線性SVM 最佳參數。在搜索段間分段采用二分法迭代求解每段線性SVM 的最高正確率以得到相應的最佳參數?。設定C 的迭代精度，如果當前C 的搜索范圍寬度不大于C 的迭代精度，則表示已經達到預定的精度，不需要在該搜索段進行更細致的二分。對于不同數據集，C的迭代精度取值可變。

5）從所有搜索段中尋找線性SVM 最佳參數。找出所有搜索段的線性SVM 最高正確率的最大值，其對應的最佳參數?記為線性SVM 最佳參數。這樣，就實現了在整個初始搜索范圍內對線性SVM最佳參數的快速搜索，能避免陷入局部極大值的問題。

2.2.2 雙線性分段二分網格搜索法求解RBF 核的最佳參數

結合雙線性網格搜索法學習精度高和訓練量小特點，利用分段二分法能快速、精確地求解最佳參數的優點，提出雙線性分段二分網格搜索法。具體實現步驟如下：

信訪評議制度是地方信訪工作改革的重要成果，是信訪工作機制創新的有益探索。目前海寧市出臺了《海寧市信訪評議團公開評議特殊疑難信訪事項辦法》（下稱《辦法》）和《海寧市信訪評議員聘任管理辦法》兩個規范性文件對信訪評議工作的開展進行規范，但由于法律對于信訪評議制度并未予以確認，導致其缺乏效力，信訪評議與法律間的有效銜接有待加強。

3）在2）中得到的最優參數（C，γ）旁的正負22范圍內，以20.25為步長進行更精細的網格搜索，記錄最高正確率對應的(C，γ)，這就是基于RBF 核的SVM的最佳參數。

2）對于RBF 核的SVM，分別將1）中得到的，0.5代入直線方程logγ=log-logC中的C?i，用滿足方程的(C，γ)來訓練SVM，根據得到的正確率，搜索到最優參數(C，γ)；

3 實驗結果與分析

2.2.1 分段二分法搜索線性SVM最佳參數

圖1 表示的是在正確率迭代精度和C 的迭代精度固定的情況下，學習精度和取樣間隔值之間的關系曲線。圖1中正確率迭代精度固定為0.2，C 的迭代精度固定為300次。當取樣間隔值為500次時學習精度為75.7%；當取樣間隔值為1000次和2000次時學習精度為75.2%；當取樣間隔值為3000次增加到4000 次時，學習精度從74.8%下降到74.3%。可見，當取樣間隔值最小時學習精度最高，取樣間隔值增加時學習精度在整體上呈現階梯降低的趨勢。

圖2 表示的是在取樣間隔值和正確率迭代精度固定的情況下，學習精度和C 的迭代精度之間的關系曲線。圖2 中取樣間隔值固定為2000，正確率迭代精度固定為0.2，C 的迭代精度從50 次開始取值。當C 的迭代精度在50 次～400 次的范圍內，學習精度保持在75.2%；當C 的迭代精度增大到450 次時，學習精度下降為74.3%，之后學習精度趨于穩定。可見，當C 的迭代精度較小時學習精度比較高，且在一定范圍內保持不變；當C 的迭代精度再增大時學習精度急劇降低；當C 的迭代精度增大到一定值后，它的變化幾乎不影響SVM的學習精度。

圖3 表示的是在取樣間隔值和C 的迭代精度固定的情況下，學習精度和正確率迭代精度之間的關系曲線。圖3 中取樣間隔值取樣間隔值固定為2000 次，C 的迭代精度固定為300 次。當正確率迭代精度為0.1 時學習精度為73.8%；當正確率迭代精度為4 時學習精度為76.2%；當正確率迭代精度在［0.1，4］之間變化時，學習精度階梯增長。可見，當正確率迭代精度在一定范圍內學習精度保持不變，隨著正確率迭代精度的增長，學習精度在整體上呈現階梯增長的趨勢。

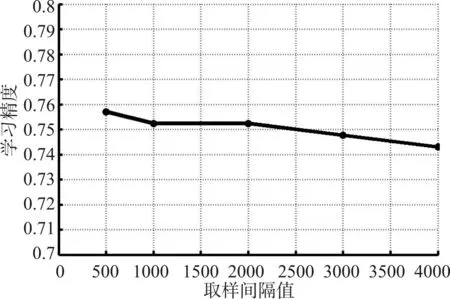
圖1 固定正確率迭代精度和C的迭代精度不變，學習精度和取樣間隔值的關系曲線

圖2 固定取樣間隔值和正確率迭代精度不變，學習精度和C的迭代精度的關系曲線

圖3 固定取樣間隔值和C的迭代精度不變，學習精度和正確率迭代精度的關系曲線

圖4 固定正確率迭代精度不變，不同取樣間隔值情況下訓練量和C的迭代精度的關系曲線

圖4 表示的是在正確率迭代精度固定的情況下，不同取樣間隔值條件下訓練量和C 的迭代精度之間的關系曲線。圖4 中正確率迭代精度固定為0.2。對于同一取樣間隔值，如取樣間隔值固定為2000次時，訓練量在整體上隨著C的迭代精度的增長而減小；對于同一C 的迭代精度，如C 的迭代精度固定為500 次時，隨取樣間隔值從500 次增加到3000次，訓練量從343次下降到319次。

分析圖1～4 結果，我們不難發現，取樣間隔值、C 的迭代精度和正確率迭代精度這三個參數要使得學習精度越高時，所造成的代價就是需要的訓練量越大。所以，這兩者不能在兩方面同時實現對SVM 最優性能的要求。不過，我們也發現，Glass數據集使用本文提出的搜索方法能獲得的最低學習精度為74.3%，最高訓練量為346 次。而后期的比較實驗，我們發現，使用雙線性網格搜索法獲得的學習精度為72.4%，訓練量為382次。所以，利用分段二分法搜索線性SVM 最佳參數，不論如何設定取樣間隔值、C 的迭代精度和正確率迭代精度，本文提出的搜索方法始終能在更小的訓練量條件下，獲得比傳統的雙線性網格搜索法更高的學習精度。

西風帶又稱暴風圈，位于副熱帶高氣壓帶與副極地低氣壓帶之間，即大約在南、北半球的35°～65°緯度，該地區的空氣運動主要是自西向東，在對流層中上部和平流層下部[1-2]。常年西風不斷，氣旋頻繁，平時最小風力大約7～8級，大多時候達到10～12級，船只航行極為危險，故又稱為“魔鬼西風帶”。西風帶在南半球更為明顯，為南極設置一道天然屏障，且是船只赴南極必經的最危險海域。

為了進一步驗證本文提出的搜索方法優越性，針對UCI 數據庫的Glass、PID、Vowel、Wine、Wdbc數據集，分別用雙線性法、網格搜索法、雙線性網格搜索法和本文提出的雙線性分段二分網格搜索法搜索SVM 模型的最優參數，從學習精度和訓練量兩方面來對表1 和表2 的實驗結果進行分析比較。其中，使用雙線性法、雙線性網格搜索法和本文方法搜索線性SVM最佳參數時，設置C的搜索范圍為［0.1，1500］；使用網格搜索法、雙線性網格搜索法和雙線性分段二分網格搜索法時，以20.25為步長對基于RBF核的SVM最優參數進行搜索。

陡河水庫1976年震后修復時只把土壩恢復到41.0 m高程，未能按設計44.0 m高程實施，防洪標準偏低，1978年被水電部列為全國43座重點病險水庫之一。1989年提高保壩標準建設，土壩加高3 m。首先對1970年震后修建的壩體回填質量在不同的斷面鉆孔取樣進行物理力學試驗，其結果滿足設計要求。因此加高前僅將表層土清除，選與原壩料相同的土料進行壩體加高填筑。土方施工基本機械化，在土方填筑碾壓后采用核子密度儀進行質檢。經檢驗，土壩碾壓干容重控制點1 159個，干容重皆遠超過設計干容重1.75 t/m3的要求。

3.3.4推進廁所革命 支持長江經濟帶11個省(市)推進農村戶用衛生廁所改造、加強農村公共衛生廁所建設、配套搞好農村廁所糞污處理。

表1 中列出使用四種搜索法得到的學習精度的實驗比較結果。雙線性分段二分網格搜索法與雙線性法、網格搜索法、雙線性網格搜索法相比，五個數據集獲得的學習精度相對于其他三種方法均有不同程度的提高。其中，Glass 數據集的學習精度相對于雙線網格搜索法提高了3%。

表2 中列出使用四種搜索法得到的訓練量的實驗比較結果。以PID 數據集為例，表中的333 代表使用雙線性分段二分網格搜索法總的訓練量，21代表使用分段二分法搜索線性SVM 最佳參數的訓練量，40+272=312 代表使用局部雙線性網格搜索法的訓練量。可以看出，雙線性分段二分網格搜索法在獲得比網格搜索法和雙線性網格搜索法更優學習精度的前提下，訓練量有明顯的減少。雙線性分段二分網格搜索法的訓練量比雙線性網格搜索法平均下降了15%以上。

表1 學習精度比較結果

表2 訓練量比較結果（訓練SVM的個數）

從表1 和表2 可看出，提出的雙線性分段二分網格搜索法與雙線性網格搜索法相比，對于各種不同復雜程度的數據集，在訓練量更小的情況下均能獲得更高的學習精度。由于雙線性網格搜索法本身綜合了雙線性法和網格搜索法的優點，訓練量介于兩者之問，學習精度幾乎達到了網格搜索法的精度。因此，可以得出，通過雙線性分段二分網格搜索法找到的最優參數使得SVM 具有更優性能，該方法相對于傳統的三種搜索方法具有更好的性能，在實際模式識別應用中是有效性的。

即使在這樣的情況下，揚州仍在堅守著，一天過去，傷亡過半，兩天過去，婦女也走上戰場。而有的人家知道抵抗無益，卻又不愿投降，害怕女性被玷污，甚至出現了舉家女性投井這種慘烈的事。四處是鮮血、尸體，但是揚州城內卻沒有出現搶掠，秩序井然有條。我被眼前的場景驚呆了，也不知道自己該何去何從。

(1) 構建判斷矩陣。計算單排序時，不同因素之間的判斷比較可簡單量化為兩兩因素之間模糊對比，量化方法引入1～9標度法，并寫成矩陣的形式，其標度及含義如表1所示。

融資方面，紹興城投直面困難，克服困難.吸取2012年的成功經驗，不斷拓寬融資渠道，轉變融資思路，更加注重政策性銀行融資與直接融資.例如，抓好二期城投債的發行，積極申報發行中期票據、短期融資券、定向私募債券等，積極爭取保障性住房貸款政策，積極爭取資產注入，擴大資產規模等.

4 結語

SVM 參數選擇將直接影響到分類器性能好壞。通過常用的雙線性法、網格搜索法、雙線性網格搜索法和本文提出的雙線性分段二分網格搜索法搜索SVM 的最佳參數的對比實驗，驗證了本文提出的搜索方法針對不同復雜程度的數據集的SVM參數優化是有效的，能為機器學習提供一定的幫助。

繼續深化農業種植結構調整。在對接河南省委、省政府“四優四化”要求的基礎上，繼續調整農業種植結構，擴大新增特色種植，大力發展新型產業。深化與河南省農科院、華大基因研究院等研究機構合作，強化優質小麥、谷子、花生等農作物新品種選育。

利用分段二分法搜索線性SVM 最佳參數時，如何根據實際數據集特點自適應設定最合適的取樣間隔值等參數，目前仍處于試驗階段，需要在更廣泛的數據集上展開應用研究。