基于改進蟻群算法的信息SNP 選擇算法研究?

顧 鑫 陳偉鶴 張付全 張 婷 蔣躍明

（1.江蘇大學計算機科學與通信工程學院 鎮江 212013）（2.無錫市精神衛生中心 無錫 214151）（3.無錫市婦幼保健院 無錫 214002）（4.無錫市第五人民醫院 無錫 214073）

1 引言

遺傳疾病是指由于遺傳物質發生改變而引發的疾病，目前遺傳疾病主要分為復雜疾病和單基因疾病兩種，復雜疾病主要包括精神分裂癥和哮喘病等，主要是因為基因中的多個單核膽酸多態性之間的相互作用而形成的，而單基因疾病則是遵循孟德爾遺傳定律。

近年來，隨著DNA 微陣列技術的不斷進步，作為檢測人類常見疾病的遺傳變異的工具，基因組范圍的關聯研究也受到了很大的關注。單核苷酸多態性（Single Nucleotide Polymorphism，SNP）是指基因組水平上由于單核苷酸變異所引起的序列多態性。SNP 擁有數量多、分布范圍廣和穩定度高等特點，常被用于復雜性狀的疾病、群體的基因識別和遺傳解剖等方面的研究，因此，SNP 已經成為第三代遺傳標記。對SNP的廣泛研究，使得像類風濕關節病和精神分裂癥等疾病的研究取得了良好的進展［1］。然而，大量研究發現兩個無關個體的99.9%的基因組序列是相似的。而剩余的0.1%的差異是導致人體產生疾病的關鍵所在［2～3］，因此對冗余的SNP 進行篩選，即從大量的SNP 中選擇具有代表性的信息SNP成為一個重要的課題。

不同遺傳標記之間存在非隨機組合的現象，例如多代遺傳中的SNP，即標記不是完全獨立的。這種現象通常存在于各種物種中，我們將這種現象稱為連鎖不平衡（LD）。在對SNP 進行篩選時，考慮到SNP維度較高以及SNP之間存在連鎖不平衡性的特點，使得傳統的機器學習方法在解決它時難免會遺漏掉許多內在的遺傳信息。針對上述場景，結合上述SNP 的特點，本文提出一種基于改進蟻群算法的SNP選擇方法，設計合理的路徑選擇函數和信息素更新機制，同時將連鎖不平衡性引入蟻群算法。

2 相關工作

目前，國內外的相關研究主要是通過生物實驗的方法從樣本中獲取SNP的原始數據，如果單純采用生物學的方法進行基因分型，將會面臨消耗時間長，代價昂貴以及難以滿足生物分析數據的要求［4～5］。當前的SNP 選擇方法有很多，比較成熟的有兩類：基于單塊的方法和基于單體型重構的信息SNP方法。

2.1 基于單體型塊的方法

考慮到理論數量遠大于人類單體型數量的基本事實，通過設定一個評價指標來衡量每個SNP，將基因組序列數據分成多個離散的單元型塊，然后根據相應的規則在每個塊中選擇相應的信息SNP。Patil 首先提出了使用貪心算法來劃分奇異塊的想法［6］。Chang 等提出了混合貪婪-劃分樹的方法，該方法引入了分支算法定界的思想，一個原始信息SNP選擇問題被劃分為多個獨立的子問題，最后構建出貪婪劃分樹［7］。Liao 提出一種多次蟻群算法選擇SNP集合，通過計算復雜度和噪聲影響同時提高劃分準確率，試驗結果表明該方法有一定改進［8］。Prathibh 提出了一種基于遺傳算法的特征選擇算法，該算法減少了特征數量，提高了基因/SNP組的特異性［9］。

2.2 基于單體型重構的方法

Bafna［10］及Halldorsson［11］首先提出了一種基于單倍型重構的SNP位點選擇方法。Halperin［12］等描述了一種用于SNP 預測和選擇的新方法STAMPA，該方法可以不必提前執行區塊劃分，因此使得方法的應用范圍更加廣闊。Lee［13］提出了基于SNP 之間的條件獨立性來標記SNP選擇的方法，通過構建貝葉斯網絡，選擇獨立和預測性高的SNP的一個子集。Ilhan［14］提出采用克隆選擇算法選擇SNP 子集，其中SNPs 之間的相似性關聯被用作其余SNP的預測方法，能夠更快的識別SNP。Alzubi［15］提出了基于條件互信息最大化和支持向量機特征遞歸消除融合的混合特征選擇方法，取得了較高的重構準確度。

3 基于蟻群算法的SNP選擇方法

根據SNP 數據分布特點和信息SNP 選擇的難點，本文提出基于改進蟻群算法的信息SNP 選擇方法，設計合理的路徑選擇函數和信息素更新機制。為了避免信息素的過分累積，從而引發局部最優，提出對信息素進行揮發，同時將連鎖不平衡性引入蟻群算法的啟發式函數，從而對SNP選擇方法進行改進。

3.1 基于改進蟻群算法的SNP子集構造

3.1.1 連鎖不平衡

目前已有多種連鎖不平衡性的測量指標，包括兩位點和多位點。以下為二等位基因位點的連鎖不平衡度量方法，假定兩個SNP位點的四種數據頻率分別為f11，f12，f21，f22，它們滿足式（1）：

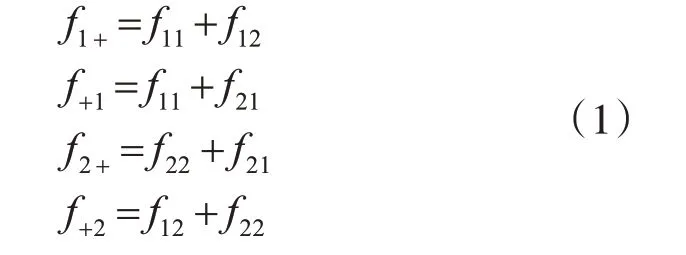
其中，f1+標識第一個等位基因為1 的單體型的頻率之和，那么連鎖不平衡度量方法如式（2）所示：

兩點連鎖度量D 值范圍太大［16］，具有相似連鎖分布的位點組合之間的D 值將會變得更大。改進的策略是對該值作歸一化后再進行度量，如式（3）所示：

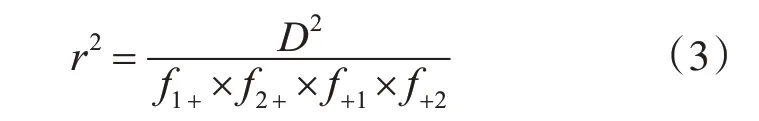
此時r2的取值位于0～1 之間。研究發現，r2能直接反應關聯研究效能，因此當前大多方法采用它作為選擇代表性SNP的依據。

3.1.2 蟻群算法基本原理

蟻群算法最初由意大利學者Dorigo M。于1991 年首次提出，它本質上是一個由仿生學計算構建的群優化系統。蟻群算法具有天然的分布式計算機制、較強的魯棒性和易與其他優化算法結合的特點。

在覓食的過程中，螞蟻將會根據信息素的濃度來決定移動的方向。因此，當環境中沒有信息素時，螞蟻的行為將是完全隨機的。而在接下來的過程中，一條路徑上經過的螞蟻越多，那么這條路徑上積累的信息素也就越多，之后的其他螞蟻因此更有可能選擇這條路徑，該過程逐漸由隨機行為轉變為智能行為。

3.1.3 路徑選擇函數

信息SNP 選擇問題中候選子集的質量取決于兩個因素：信息SNP 數量和信息SNP 對非信息SNP 重新構造的準確度。本文將這兩種因素放在路徑選擇及信息素更新過程中。螞蟻的路徑選擇采用概率機制，當前人工螞蟻選擇下一節點的概率如式（4）所示：

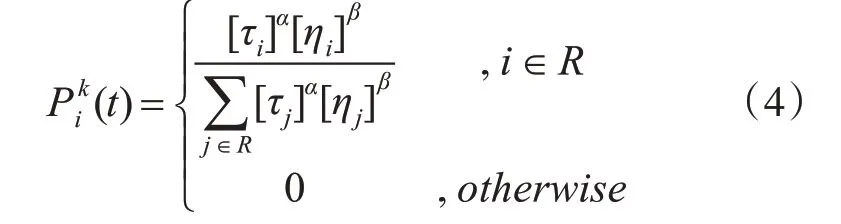
其中τi和ηi分別表示節點信息素濃度和節點當前的啟發信息，而α和β分別為信息素和啟發因子的權重參數，R 表示本次迭代過程中沒有被選中的SNP 位點。可以通過調整權重的方式更新選擇機制，如當α＞β時，表示蟻群選擇路徑更側重于參考SNP位點上的信息素濃度。

3.1.4 信息素更新機制

信息SNP 選擇問題中信息SNP 數量大小可以類比于傳統螞蟻在覓食過程中走過的路程，路程的長度越短則表明SNP 該條路徑越優秀。在相同的重新構造準確度下，信息SNP 的數量越小，SNP 子集越好，位點上的信息素類似于自然界中螞蟻留下的化學物質。信息素累積函數如式（5）所示：

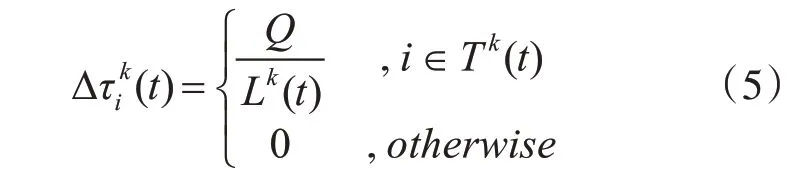
其中，Tk(t)表示第k只螞蟻在第t 次迭代過程中所構造的候選信息SNP 子集，Q為原始數據集中的所有SNP 數量。Lk(t)表示路徑的長度，即子集中包含的SNP數量。

信息SNP 選擇問題也與天然螞蟻覓食過程不同，信息SNP選擇過程是跳躍的，相反，螞蟻可以從當前節點跳轉到任何其他節點，并且構造的候選子集具有無序性，即選擇SNP的順序不影響子集的質量。

為了防止信息素在某些位置疊加并引起局部最優，必須適當削弱位點的信息素。本文模擬自然環境中的空氣流動，引入了信息素揮發機制，通過式（6）實施螞蟻和信息素蒸發添加新信息素：

?τi( )

t表示迭代后式（2）中在所具有的信息素，并且被設置為路徑上的總信息素的初始值。

信息素揮發系數ρ是螞蟻留在路徑上的信息素的持久權重，揮發系數越小表示信息素每次迭代過程中損失越小，信息素越不容易消失，留下的信息素越多。通過調整揮發系數，可以在一定程度上降低信息素的過度累積，從而盡量避免蟻群算法在后期陷入局部最優。考慮到該算法在初始階段較差的尋優能力，在得到更好的解后引起局部最優，因此提出一種新的信息素揮發因子。具體調整如式（7）所示：

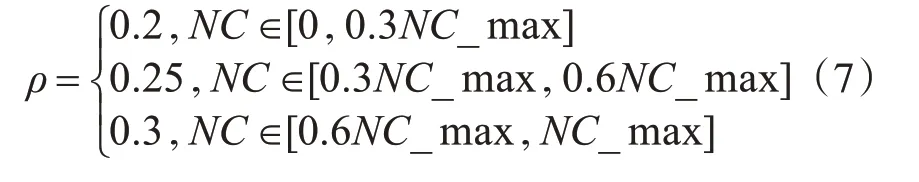
式（7）中，NC_MAX 表示蟻群算法的最大迭代次數，為固定值。NC 表示蟻群算法在本輪的迭代次數。在迭代初期，通過設定較小的信息素揮發系數可以加快收斂速度，而在算法的中期和末期，適當增加信息素揮發系數的值避免局部最優。

3.1.5 啟發式函數

信息SNP 子集的優劣可以由重構準確度來測量，其中Ci為兩位點連鎖不平衡度量，如式（8）所示：

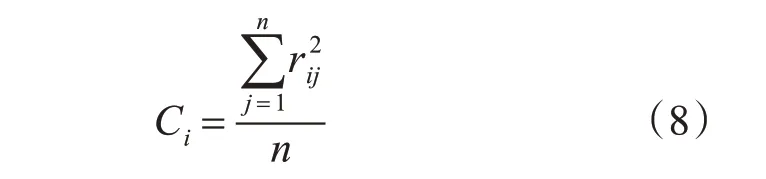
本文中兩位點連鎖測量使用式（3）的r2。其中表示兩個位點i 和j 之間的連鎖值，而n表示已經選中位點的數目，Ci為位點i和已經選中位點的連鎖值的平均值，介于0～1 之間。值越大，該位點具有更強的連鎖性，則更有利于成為信息SNP。

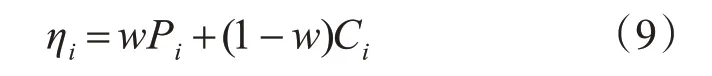
Pi表示信息位點i 對其它所有非信息SNP 位點重構準確度的平均值。將Pi和Ci的加權組合作為啟發式信息，修改w的值可以調整Pi和Ci權重。

3.1.6 蟻群算法構造信息SNP子集的偽代碼

以下使用偽代碼來描述用于選SNP 子集的蟻群算法的總體框架。當方法達到最大迭代次數或達到重構準確度時退出。

基于蟻群算法的信息SNP 子集構造

輸入：個體基因型數據或單倍型數據

輸出：信息SNP 集合

Begin：

初始化信息素和參數;

Nc=0；

While(Nc＜=Nc_max)

For i=1 to n_ants //n_ants為螞蟻數量

//每只螞蟻分別逐個添加SNP到候選信息SNP

While(prediction accuracy is not enough)

計算ηi；

按式（4）在候選SNP選擇新的SNP位點;

End while

保存本次迭代過程中的最優解；

End For

2.1 兩組血漿NT-proBNP水平比較 病例組患兒的NT-proBNP水平在治療3 d、治療7d 、治療14 d時均顯著低于組內治療前(F=176.405，P<0.05)，病例組患兒的NT-proBNP水平在治療前、治療3 d、治療7 d、治療14 d時均顯著高于對照組(F=286.557，P<0.05)。見表1。

//每只螞蟻結束尋找路徑后，根據已經經過的節點數目

計算這些節點上每只螞蟻留下的信息素

按式（6）計算新的信息素;

Nc++；

End while

返回候選SNP;

End

3.2 基于KNN的SNP預測

本文采用K-最近鄰（KNN）方法來預測未選擇的SNP。給定測試集d（其類別未知），該方法是在訓練集中查找k 個最近鄰居，并且使用k 個最近鄰居的類別來對候選者進行預測。在本文中，兩個SNP 基因序列之間的距離為漢明距離，必須確定基因型之間k 個最近的鄰居。本文設定為5-NN（k=5），即確定投票過程的基因型樣本的5 個鄰居，并通過對這五個鄰居進行投票獲得預測樣本結果。整體過程如圖1所示。

4 實驗

4.1 實驗數據和環境

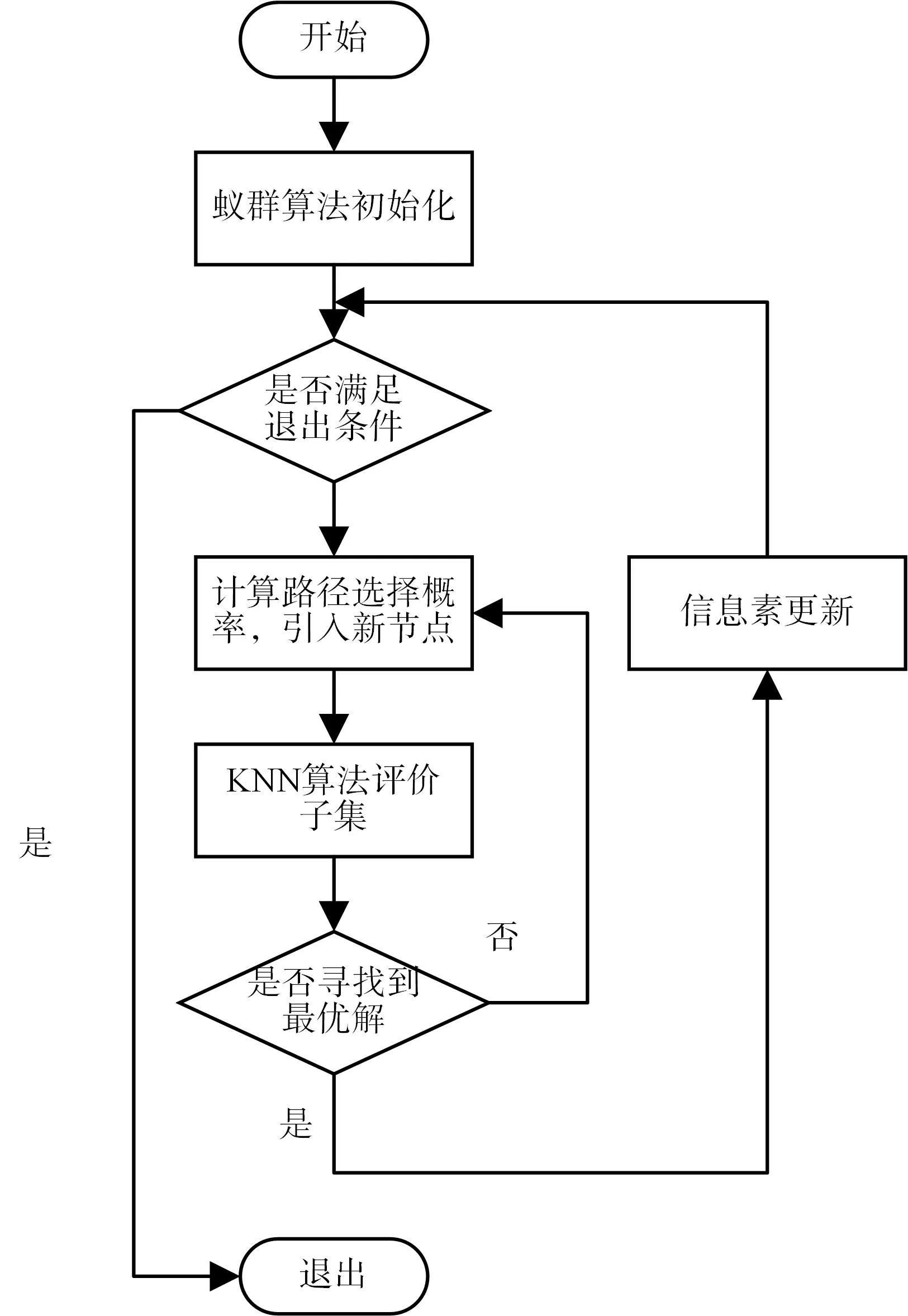
圖1 SNP選擇流程圖

實驗數據本實驗中所使用的數據由無錫市精神衛生中心提供。數據格式為遺傳病的SNP 基因型格式，并且每個樣本都帶有標記信息，標記樣本是否患病。數據集的概況描述如表1所示。

表1 數據集描述

4.2 實驗評價指標

本文使用信息SNP 子集對非信息SNP 子集的重構準確度（ACC(I)）作為信息SNP子集的評價指標，其定義如式（10）所示：

其中gi為位點上的實際值，為預測出的值，兩者差的絕對值即為預測誤差。N 是樣本的數量，是非信息SNP 的數量，兩者積為總重構次數。重構度越高，信息SNP子集對非信息SNP的預測效果越好。

4.3 SNP數據編碼

由于實驗的原始數據是SNP的基因型表示，本次實驗采用的編碼方式是“0-1-2”編碼，分別表示AA、Aa以及aa。編碼完成后，對缺失值需要進一步進行填充。考慮到SNP局部可能存在關聯性，所以使用K近鄰的方式對其進行填充。

4.4 實驗結果與分析

Halperin 等設計了一種最大投票法STAMPA，將此方法用于對結果的重構，每個位點根據其最相似的信息SNP 位點預測［18］。粒子群算法BPSO［19］類似于本文中候選子集構造的蟻群算法，BPSO 和STAMPA 組合為BPSO/STAMPA，與MLR 的組合是BPSO/MLR，本文方法蟻群算法與最近鄰分類組合標記為ACO/KNN，蟻群算法參數設置為α=1、β=3，螞蟻數量設置為10，迭代次數為10。

4.4.1 重構準確度

三種方法在兩個數據集上的實驗結果如圖2和圖3 所示。在圖中，橫坐標是信息SNP 的數量，縱坐標是重構準確率。可以看出，在該數據集E144 中，所提出的方法和BPSO/MLR 的準確度明顯優于BPSO/ STAMPA，ACO/KNN 與BPSO/MLR的重構準確度效果相似。在數據集G1000中，該方法具有比BPSO/STAMPA 和BPSO/MLR 的更高的重構準確度，并且重構準確度平均高出2%～5%。BP?SO/MLR 略高于BPSO/STAMPA，ACO/KNN 引入了連鎖度，使得位點間的連鎖不平衡性較高。可以得出本文方法更能獲取有利于樣本重構的特征。

圖2 數據集E144上重構準確度

4.4.2 運行時間

分別使用ACO/KNN、BPSO/STAMPA 和BPSO/MLR 三種算法在兩個數據集上進行實驗，并比較每種算法的運行時間，其結果如圖4和圖5所示（每組實驗重復三次并對結果取均值）。在圖中，橫坐標是信息SNP 的數量，縱坐標是運行時間（單位：s）。由于E144 數據集規模大于G1000 數據集，因此運行時間也大于G1000 數據集。從圖中可以看出，隨著SNP 數量的增加，該方法的優勢也逐漸明顯。

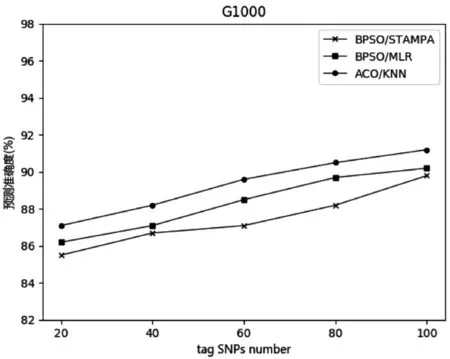
圖3 數據集G1000上重構準確度

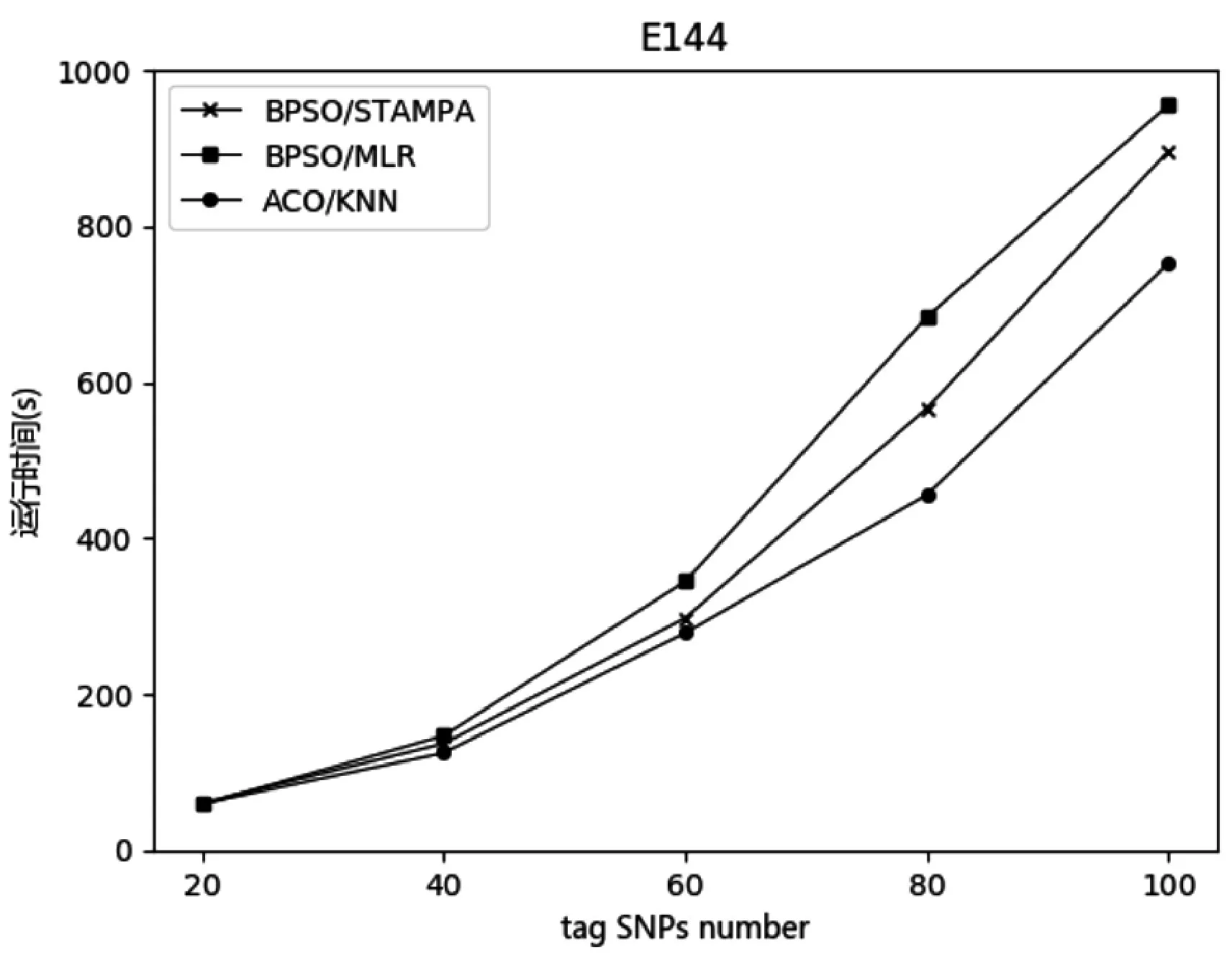
圖4 數據集E144上運行時間

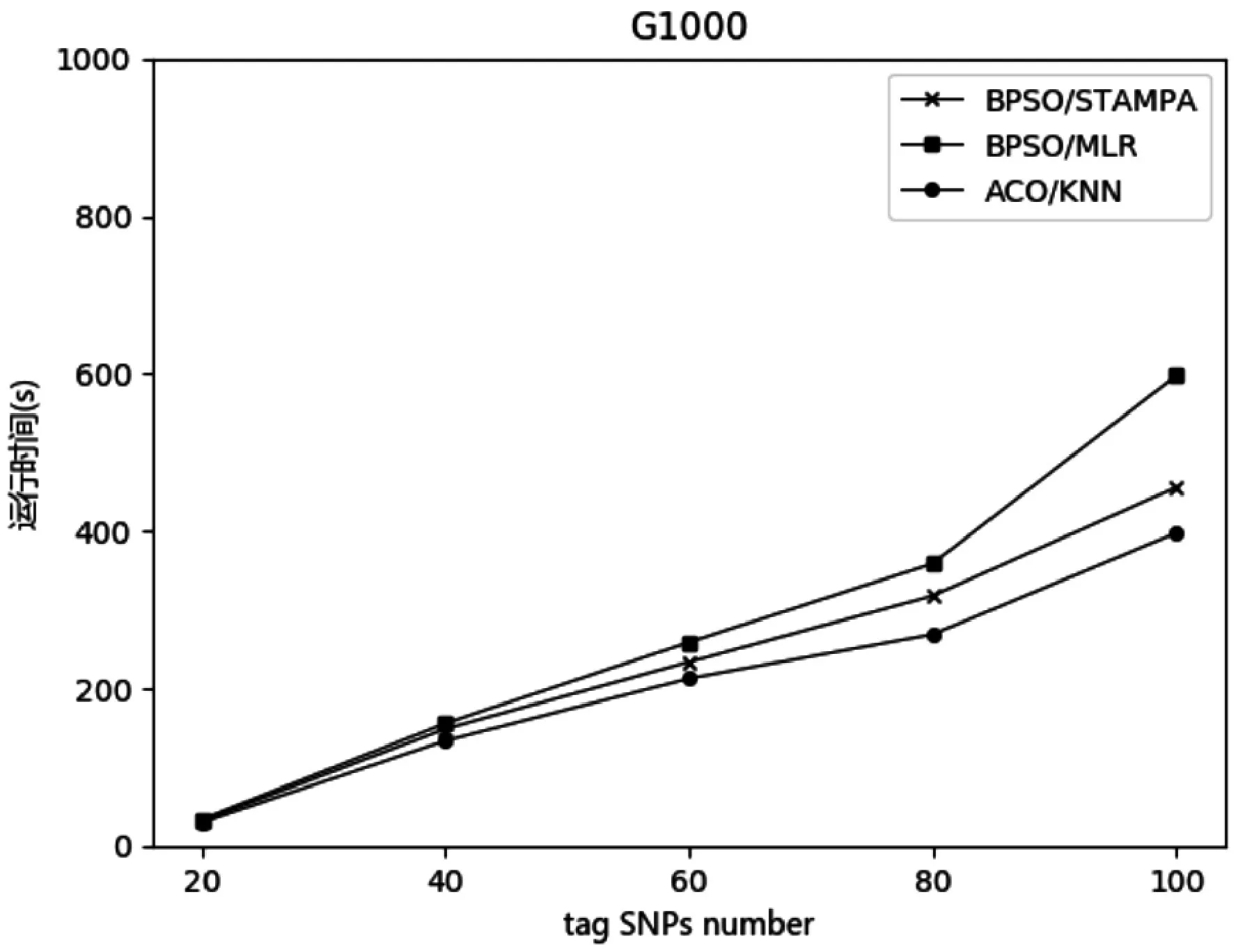
圖5 數據集G1000上運行時間

5 結語

在本文中，針對SNP 數據普遍存在的少樣本、高維度的問題，和不同SNP位點之間存在連鎖不平衡導致的位點之間具有強相關性的特點，將連鎖不平衡性應用到蟻群算法中，提出一種基于蟻群算法（ACO）信息SNP 選擇方法。本文使用的實驗數據來自無錫市精神衛生中心，并與文獻中的SNP選擇方法作了比較。本文的后續工作是對KNN 進行改進，使篩選出的信息SNP子集具有更高的重構度。