中國剩余定理相位解包裹方法的改進?

趙甜甜 李 鋒

（江蘇科技大學電子信息學院 鎮江 212003）

1 引言

光柵投影測量是三維測量方法的一個重要分支，因其具有非接觸、低成本和高精度等優點，被廣泛應用在光學三維測量領域［1～3］。由此方法得到的相位是立體匹配的一個特征［4］，結合系統標定參數，再根據三角法進行計算就可以得到被測物體三維信息。該方法的關鍵問題之一就是如何正確地獲取待測物體的相位。目前最常用的測量相位的方法就是相移法，該方法具有較高的測量精度，但是相位被包裹在一個周期內，在整個測量空間呈鋸齒狀分布，必需將包裹相位展開。目前，相位解包裹技術主要有兩種［5～6］，一是空間解包裹技術，二是多頻解包裹技術。

空間相位解包裹只需要一幅包裹相位圖，但是只有在理想情況下（被測物體輪廓簡單，信噪比足夠高）才能正確地獲得絕對相位圖。多頻相位解包裹是假設在時間一致的條件下，通過向被測物體表面投影一系列不同的光柵條紋，然后對相機拍攝到的編碼圖案解包裹確定絕對相位值。其典型的方法有小數重合法、時間解包裹法、外差法和基于中國剩余定理（Chinese Remainder Theorem，CRT）的方法。因解包裹相位的實質為求解編碼點的像素坐標對不同頻率的包裹相位和頻率構成的同余方程組的問題。而中國剩余定理根據系列模數和對應的剩余，采用簡單的運算獲得被除數，是求解同余方程組的有效方法，且可以實現最大范圍解包裹，計算效率高。因而，基于中國剩余定理解包裹相位的方法吸引了國內與國外專家的普遍關注與研究。

Cushov［7］等初次將中國剩余定理應用于光學干涉儀相位輪廓測量，計算絕對相位存在偏差。Takeda［8］等 對Gerohbery-Saxton 算 法 做 出 了 改 進，提出了自適應高度偏移聯合誤差校正查找表修正較大偏差的方法。Zhong［9］等采用比值為無理數的兩個頻率在一定范疇內獲得所有折疊整數的同余結果，并保留誤差值，根據閾值進行選擇符合條件的折疊整數作為最優結果。Towers［10］等假設在相位誤差存在上、下限的條件下，遍歷搜索絕對相位誤差，根據測量范圍約束確定最優結果。Xia［11］等提出了健壯中國剩余定理，但是該方法需要進行二維搜索，增大了計算成本。Wang［12］等在此基礎上進行改進，將該定理從整數域擴充到實數域，可以進行封閉式求解。張旭［13］等通過分析亮度噪聲對包裹相位的影響，提出了選頻準則。文獻［14］提出了基于CRT 選頻準則的微相位測量輪廓術。于曉洋［15］等提出了一種CRT 工程化求解方法。但是存在抗干擾能力差，測量誤差比較大的缺點。而且測量范圍只適用于模互質和模存在最大公約數不為1 的情況，并沒有對模非互質又不存在公約數的情況進行求解和分析。

因此，為了解決上述現有關于中國剩余定理解包裹存在的問題，本文提出了一種改進的中國剩余定理工程化求解方法。首先，本文采用標準四步相移的方法獲取包裹相位，降低了包裹相位中存在的誤差，提高了測量精度。其次，通過采用合并方程組的思想求解同余方程組，此方法既能計算模非互質又不存在公約數的情況，又能計算模互質和模存在最大公約數非互質的情況，擴大了中國剩余定理解包裹的應用范圍，同時提高了測量速度，增強了抗干擾能力。

2 基于改進的CRT相位求解

本文采用標準四步相移作為獲取包裹相位的方法，其波動范圍為［0，2 π］，需要進行相位解包裹。從標準四步相移計算包裹相位的計算公式中，可以看出其具有消除背景光照和常數項影響的優點，對投影儀的非線性起到抑制作用，減小了系統誤差，具有測量精度高、抗干擾能力強的優點。

2.1 中國剩余定理原理

設np、ri、pi為整數，i=1，2，…，k ；令ri為np對模數pi取余后的余數。當各pi之間不一定互質時，采用合并方程的思想進行求解同余方程組。設k1、k2、…、ki為整數，滿足：

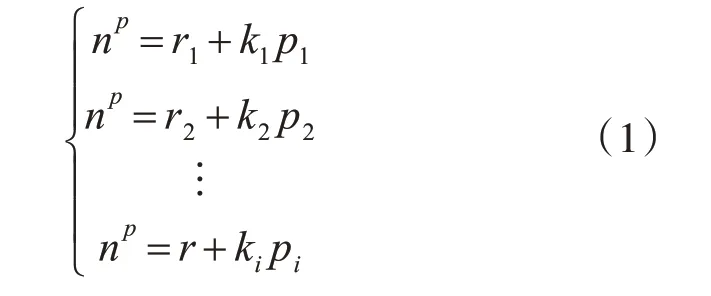
首先，合并公式np=r1+k1p1，np=r2+k2p2整理化簡得：

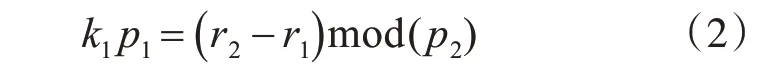
顯然，要想有解，必須gcd(p1，p2)|(r2-r1)。令gcd(p1，p2)=d ，r2-r1=C ，則有

依次類推迭代下去，最終求得k 個方程的最小正數解np為r%p。

實際求解絕對相位時，包裹相位和絕對坐標值都不是整數，而是實數。因此需要將CRT應用范圍從整數域擴充到實數域。首先，對輸入的模數pi即編碼周期進行分析，設最大公約數為d ，當pi兩兩互質時，d=1；當pi存在最大公約數不為1 時，d= gcd (pi，pj)≠1(1 ≤i≠j≤k) ；排除上述兩種情況，d=1。其次，設ri、np為實數，ri為余數即包裹相位，np為絕對坐標值。ri可以分解為riod+ric，其中rio為整數、0 ≤ric＜d。在理想情況下，即ri沒有誤差，所有的ri都是相等的，則riod也是相等的，ric相等，記為rac。有：

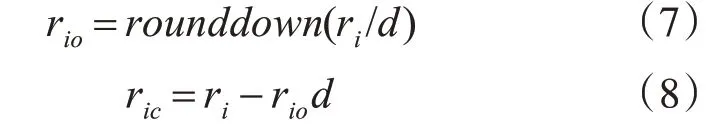
式中：rounddown()代表向下取整。最后，將rio代入式（1）替換余數ri，通過合并方程的方式求解出整數解np，與riod對應的整數解為npd。因為ri比riod大了rac，令rc=rac/d，0 ≤rc＜1。所以中國剩余定理的實數解為

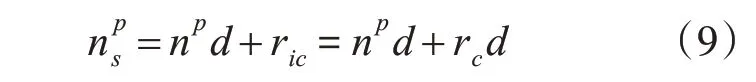
通過式（1）～（9），將CRT 應用范圍推廣到對模數沒有任何要求的情況，并且在實數域范圍內對同余方程組進行求解。

2.2 小數差判據

實際工程中，設ri為包裹相位，其存在誤差不相同，需要考慮CRT求解的準確性問題。

定義包裹相位ri的誤差為|，如果，則rio會偏離原位置，只要不全部相等，必然會導致np求解失敗。因此，，是求解正確的前提。設變換后的包裹相位誤差和包裹相位分別為，即：r?i的整數部分為bio，小數部分為bi，則

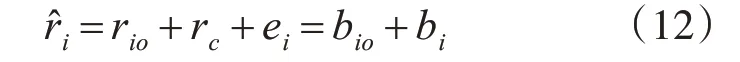
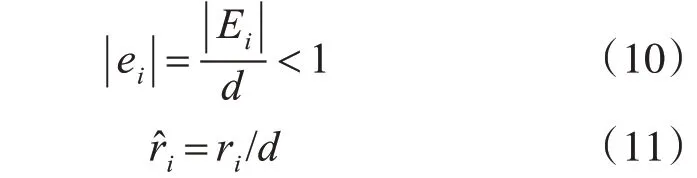
根據ei和rc的不同情況，r?i=bio+bi有三種情況：1）當0 ≤ei+rc＜1 時，bio=rio，bc=ei+rc；2）當1 ≤ei+rc＜2 時，bio=rio+1 ，bi=ei+rc-1 ；3）當-1 ＜ei+rc＜0 時，bio=rio-1，bi=ei+rc+1。分析每種情況，bi都是(ei+rc)和整數的和，則包裹相位小數部分之差?bij=bi-bj(1 ≤i≠j≤k)為包裹相位誤差之差(ei-ej)與整數的和，所以?bij可以描繪出包裹相位誤差之間的差異。bi、bj與分別對應，且分別有三種情況，所以?bij=bi-bj有九種組合：（1）和都屬于1），?bij=ei-ej；（2）和都屬于2），?bij=ei-ej；（3）和都屬于3），?bij=ei-ej；（4）屬于1），屬于（2），?bij=ei-ej-1 ；（5）屬 于1），屬 于3），?bij=ei-ej-1 ；（6）屬 于2），屬 于1），?bij=ei-ej-1 ；（7）屬 于 2），屬 于 3），?bij=ei-ej-2 ；（8）屬 于3），屬 于1），?bij=ei-ej+1 ；（9）屬 于3），屬 于2），?bij=ei-ej+2。

第一類情況I，包含組合（1）、（2）和（3），為

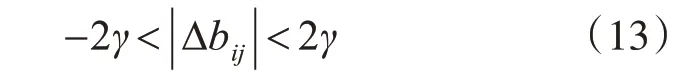
第二類情況II，包含組合（4）、（5）、（6）和（8），為

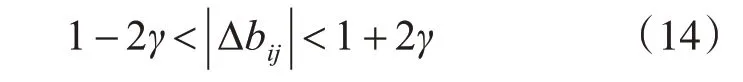
第三類情況III，包含組合（7）和（9），為

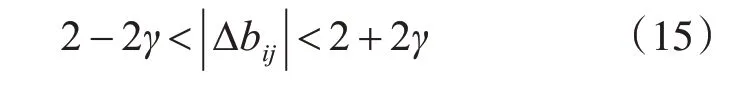
可以看出-2γ＜1-2γ＜2-2γ、2γ＜1+2γ＜2+2γ，通過限定γ使式（17）成立。

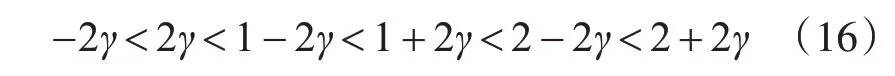
這樣可以通過| ?bij|來區 分I、II 和III，求得γ＜0.25 ，即 |ei|＜0.25 。又 因 為0 ≤bi＜1 ，所 以0 ≤| ?bij|＜1，而2-2γ＞1，所以Z 類情況不存在。即：

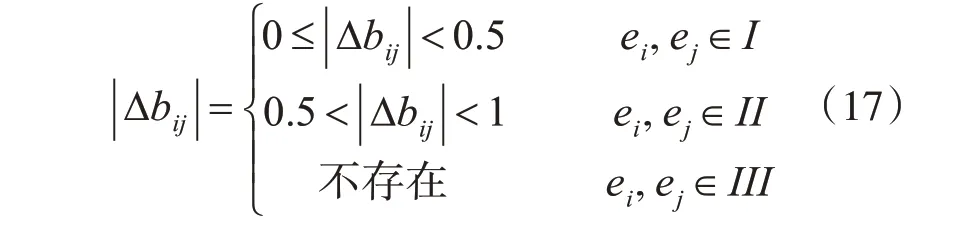
根據式（10）可得，當編碼周期存在最大公約數d時，包裹相位誤差限定為。

2.3 取整方式

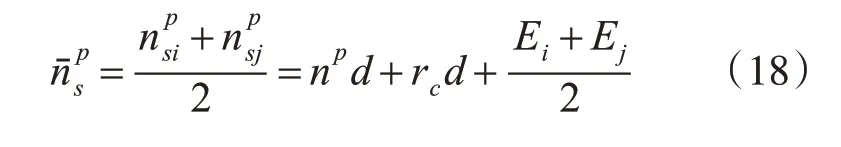
根據式（18），可以看出實數解的誤差為(Ei+Ej)/2，小于誤差 |Ei|和 |Ej|之間的最大值。同理，對其余兩種情況進行分析也是滿足上述結論的。

i 帶入求得第i個模數pi的實數解==(np+1)d+ (rc+ei-1)d=npd+(rc+ei)d，同理，+=npd+(rc+ej)d。在根據式（18）獲得最終實數解=()/2 =npd+rcd+(Ei+Ej)/2，誤差仍然為(Ei+Ej)/2。同理，求解其余三種情況，得到如下結論：當0.5 ＜1，對包裹相位進行四舍五入取整，可以正確求取實數解，不存在求解失敗的現象，其誤差為(Ei+Ej)/2。

當存在k個模數時：首先判斷所有小數部分的差值，如果所有的最大值小于 0.5 ，則 對 所 有r?i進 行 向 下 取 整，即rounddown(r?i)，將其作為余數測量值整數按照前面所述的過程進行計算，得到的實數解誤差為如果所有的最大值大于0.5，則對所有進行四舍五入取整，即round(r?i)，獲得的實數解誤差仍然為

總結上述分析，使用改進的CRT進行準確求解的條件為：當包裹相位測量誤差＜d/4 時，即＜0.25，如果所有的最大值小于0.5，則所有的rio=rounddown(?)，如果所有中最大值大于0.5，則所有的rio=round(r?i)。將取整結果帶入式（1），合并方程組進行求取整數解np，根據式（9）、（18）得到實數解，其誤差為

2.4 改進CRT算法步驟

本文改進的CRT 工程化算法可以分為以下幾步。

步驟1：計算所有變換后包裹相位? 之間的小數部分之差。步驟2：當所有中的最大值小于0.5 時，將所有包裹相位?向下取整；當所有中的最大值大于0.5 時，對所有的包裹相位? 采用四舍五入的方式進行取整。

步驟3：將包裹相位的取整結果帶入式（1），采用合并方程組的思想，求取絕對坐標整數解。

步驟4：令rc為包裹相位與其取整結果之差，根據式（10）求解獲得第i個模數pi的實數解。

步驟5：利用式（18）解得同余方程組的實數解，即編碼圖案絕對坐標值。

本文CRT 求解算法既可以求解模數非互質的情況，也可以求解互質的情況，具有解析求解、運算簡單、求解快的優點。

3 仿真與實驗分析

3.1 仿真分析

為了驗證本文方法的可行性，選取三個周期T1=13，T2=15，T3=18，最大展開范圍為1170pix?el。在Matlab2017a 中采用標準四步余弦相移的方法產生條紋圖形，大小為1024pixel×768pixel，并在上面分別添加高斯分布隨機噪聲，計算得到三個不同周期下的包裹相位a1，a2，a3。根據包裹相位ai和周期Ti，采用本文方法獲取編碼圖案絕對坐標。

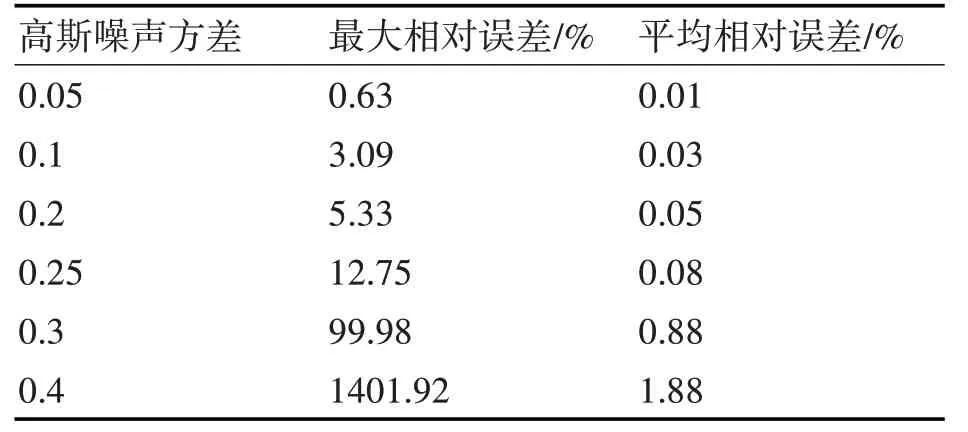
表1 不同方差高斯隨機噪聲下的相位解包裹結果

表1 為對條紋圖形歸一化后，分別加入不同方差的高斯隨機噪聲誤差，與未加入噪聲誤差的條紋圖形求取編碼圖案絕對坐標進行比較。為進一步證明實驗數據的有效性，本文對無噪聲的條紋圖形進行30 次求解取其平均值帶入計算，同樣對加入不同方差的隨機噪聲得到的條紋圖形進行30 次求解取平均值。從表1 中可以看出，在隨機噪聲方差不大于0.25 時，最大相位誤差不大于12.75%，平均相對誤差最大為0.08%，從而看出使用本文方法求解出絕對坐標值的精確度較高，抗干擾能力強，驗證了本文方法在求解周期即不互質也不存在最大公約數不為1 情況下的可行性。但當隨機噪聲方差大于0.25時，求解平均相對誤差和最大相對誤差急劇增大，求解得到的絕對坐標值精確度大幅降低，出現絕對坐標值的跳變。當隨機高斯噪聲方差為0.25 時，對模擬包裹相位進行求解，其結果如圖1（a）為求解得到的絕對坐標面型圖，（b）為選取第600 行的絕對坐標圖。從圖1 中可以看出，存在較大隨機噪聲時，使用本文方法依然能精確地對包裹相位進行展開。從理論上驗證了本文方法在求解非互質周期且最大公約數不為1的可行性。

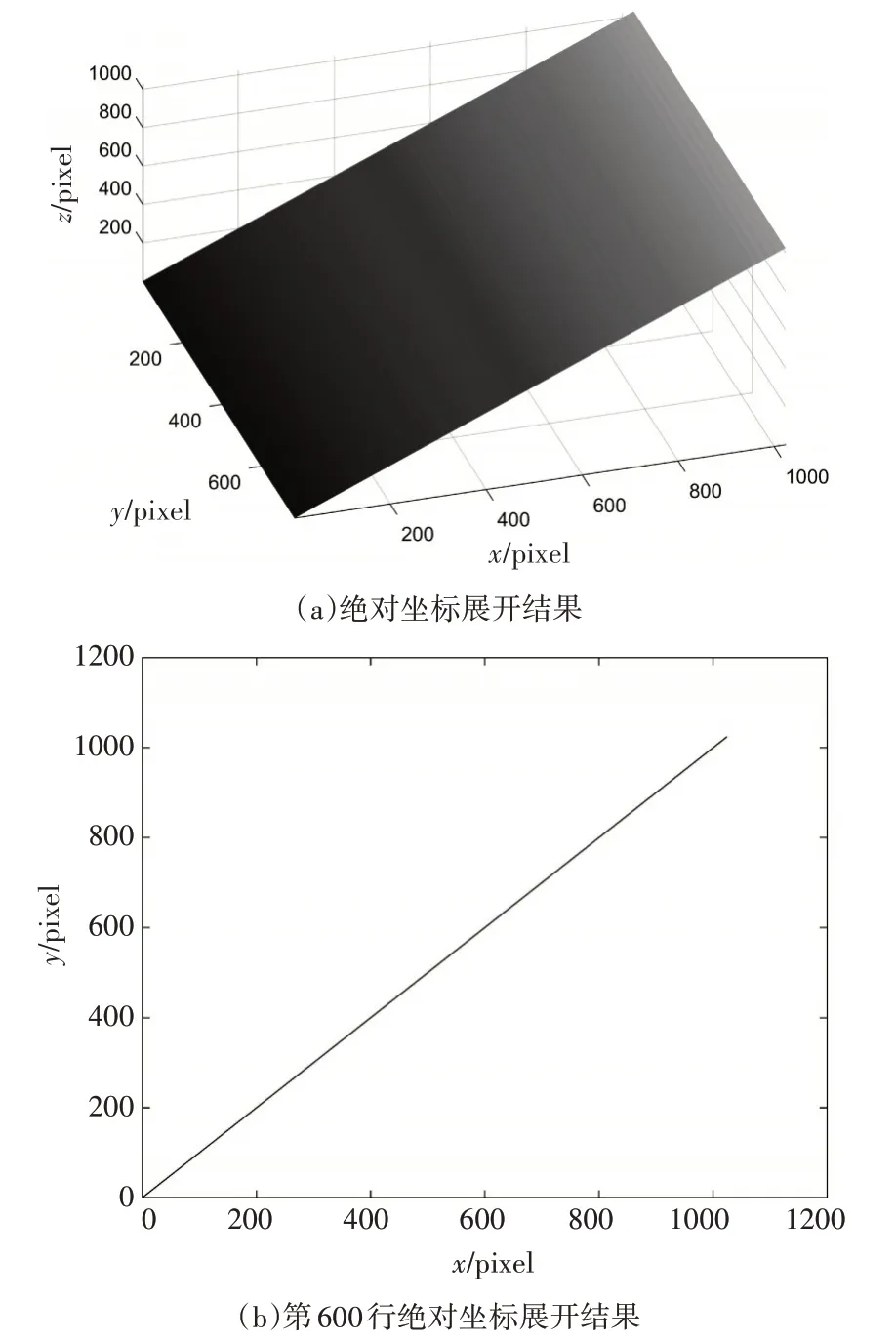
圖1 相位展開結果

3.2 實驗分析

為了進一步驗證本文方法的有效性，構建了一套由EPSONEB-C760X 投影儀（分辨率為1024pixel×76 8pixel）、單個AVT相機Manta G-125（分辨率為1292pixel×964pixel）和一臺個人電腦組成的結構光測量系統（Windows7，Matlab2017a），如圖2所示。

圖2 結構光測量系統

采用搭建的實驗平臺，向標準白板投射周期為13、15、18 的光柵圖像，采用本文算法得到絕對相位，從而對該平面進行三維重建，重構出來的平面表面光滑，點云分布均勻。對其進行平面擬合，得到結果的最大絕對偏差為1.96mm，平均絕對偏差為0.546mm。

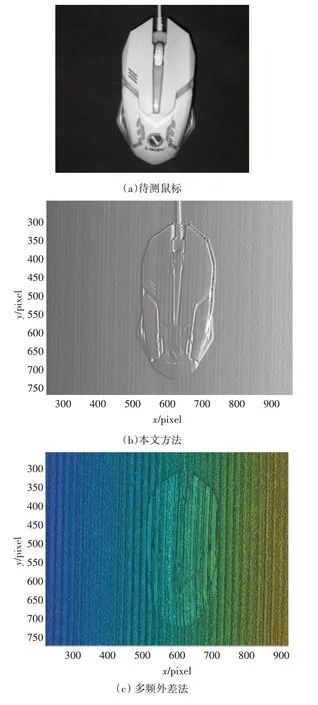
圖3 鼠標及其相位展開結果

對圖3（a）中的鼠標進行測量。本文算法與多頻外差法、基于CRT的三步梯形相移法［16］進行對比實驗，在相同環境下，直接對獲取的產生畸變的條紋圖案進行求解包裹相位。圖3（b）、（c）、（d）分別為采用三種方法獲得的絕對相位圖。圖3 表明，多頻外差法和基于CRT 的三步梯形相移法抗噪聲能力差，解析得到的絕對相位圖上出現明顯的噪點，輪廓不清晰，且對系統的非線性抑制能力弱。而本文方法求解出來的絕對相位，表面光滑，物體輪廓清晰，除去由物體陰影部分產生的誤差，表面沒有噪點。本文方法明顯優于圖3 中其他方法，具有抗干擾能力強，求解精度高的優點。圖4 為使用本文方法得到的三維測量結果。

圖4 鼠標測量結果

表2 給出了本文方法與多頻外差法、基于CRT的三步梯形相移法相位解包裹所用的平均時間，可以看出本文方法在測量時間上也是優于其他方法的。

表2 不同方法的相位解包裹時間

4 結語

現有的基于CRT 相位解包裹方法對輸入的包裹相位誤差非常敏感，且不能對非互質頻率的包裹相位進行求解。由于對包裹相位誤差敏感，本文采用標準四步相移法獲取包裹相位，減小了系統誤差，增加了抗干擾能力。通過包裹相位測量值的小數差選擇取整方式，并在計算整數解時采用合并方程組的思想。本方法無需限定輸入頻率，從而擴展了中國剩余定理解包裹相位應用范圍。仿真和實驗以及對比分析結果表明，本文方法運算簡單，求解速度快，同時抗干擾能力強，求解精確度高。但是該方法限定了包裹相位測量誤差，對包裹相位誤差大時要采用其他措施