相依失效生命線工程系統抗震可靠度估計的統一RDA 算法

顧 倩，夏 恒，何 軍

(上海交通大學船舶海洋與建筑工程學院，上海 200240)

生命線工程系統是對維系城市經濟發展和社會生活具有重大影響的基礎性工程設施系統，如交通、通訊、供水、供電、煤氣和輸油等工程系統。根據網絡理論，生命線工程系統的網絡模型由四個要素構成，即節點、線路、流量和賦權形式。而根據網絡賦權形式的不同，網絡系統可分為邊權網絡(只考慮邊型生命線構件或結構的地震失效)、點權網絡(只考慮節點型生命線構件或結構的地震失效)和一般賦權網絡(同時考慮邊型和節點型生命線構件或結構的地震失效)。

在生命線地震工程中，將系統的抗震可靠度定義為地震作用下生命線系統拓撲網絡中源點到終點的連通可靠度。一般的生命線工程系統往往具有多個源點和多個終點，如上海供水管網系統包含多個水廠和多個用戶端。對于這一問題，可通過設置一個單向聯結各源點或各終點的虛擬節點的辦法將其轉化為兩終端問題[1]。此時，兩虛擬節點的連通可靠度即為原多源多匯系統的連通可靠度。為了簡化分析過程，本文僅考慮單源點到單終點的兩終端生命線系統網絡連通可靠度問題。生命線工程網絡模型規模龐大、類型多樣，導致其具有很大的復雜性。另外，地震作用下生命線工程還具有失效相關性，包括兩個方面：第一，地震動的空間相關性，即同一地震輸入對不同元件的破壞是具有相關性的；第二，系統結構形式導致的失效相關性，網絡系統中節點的失效會引起此節點相聯邊的失效，反之，與一節點相聯的所有邊的失效也相當于此節點的失效。因此，要進行生命線工程網絡系統抗震可靠度估計的研究，難點就在于其計算復雜性和失效相關性。

一方面，網絡系統可靠度的計算問題是典型的NP-Hard 問題，計算量呈現非多項式增長的趨勢。在過去的幾十年中，國內外學者圍繞著如何降低網絡系統可靠度的計算量問題展開了一系列的研究，由此產生的方法主要可分為隨機模擬法和概率解析法。早期的Monte Carlo 隨機模擬方法，在大型失效獨立網絡可靠性分析中，往往能取得較好的效果。但是，這一算法在計算工作量和算法收斂性方面存在一定的局限性[2?3]。概率解析算法是通過應用網絡分析技術，建立精確或近似的數學模型。在概率解析算法中，較為成熟的方法有不交積之和算法[4?5]、因子分解定理算法[6?8]、二分決策圖算法[9?10]以及最小路遞推分解算法[1]。這些算法在應用中有各自的適用范圍，且求解效率不盡相同。本文的研究將以遞推分解思想為基礎。該思想最早于1979 年由Dotson 等[11]提出，對降低網絡算法的空間復雜性研究起到了巨大的推動作用。后續又經過了一系列的發展，2002年，李杰和何軍[1,12?13]正式提出了遞推分解算法(RDA)，有效地降低了網絡算法的復雜性，并且能夠用于大型網絡的可靠度估計。RDA 算法的詳細介紹，將在本文第1 節中給出。

另一方面，系統中元件失效具有相關性。在生命線工程系統抗震可靠度的研究中，要考慮元件失效相關的情況，需要解決的是不交最小路(或不交最小割)事件的聯合失效概率的計算問題。解決這類問題的思路是，在已知基本隨機變量數值特征的基礎上，結合結構功能函數，計算相關失效系統的可靠度。Copula 是建立多維隨機變量聯合分布的有效方法[14]，Gumbel Copula 就是工程中常用的一種阿基米德型Copula。1981 年，Ang[15]提出了概率網絡估算技術(PNET 方法)，該方法將所有主要失效模式按彼此相關系數的大小分成若干組，在每一組中選出一個失效概率最大的失效模式作為代表模式，然后假定各代表失效模式相互獨立，再來估算網絡系統的失效概率。2000 年，Philippe[16]提出串聯系統可靠度的一階矩方法，該方法采用Cholesky 分解方法把結構功能函數的基本隨機變量進行分解，結果表明Maincon 算法的分析結果精度較高。2013 年，Won-Hee Kang 等[17]提出了SCM 算法，該算法是一種快速可靠性評價算法，主要由“與”合并和“或”合并兩種運算組成，通過這兩種運算將網絡化簡直至合并為一個點[18]，從而由最終化簡得到的節點可靠度估計系統可靠度。

本文基于原RDA 算法，先對原來分別按照邊權、點權和一般賦權，需要運用對應程序去計算系統可靠度的情況進行整合簡化，發展出同時適用于三種賦權形式的統一RDA 算法。進一步在統一RDA 算法的基礎上，引入SCM 和Gumbel Copula函數兩種方法分別計算RDA 算法中不交最小路和不交最小割的聯合失效概率，發展出相依失效生命線工程系統抗震可靠度估計的統一RDA 算法。最后，以一假想電力系統為例，將其簡化為一36 節點格柵型拓撲網絡，估計該網絡系統相依失效的動力抗震可靠度，從而驗證本文方法的有效性。

1 統一RDA 算法

本文以文獻[1]提出的RDA 算法為基礎，該算法通過引入結構函數遞推分解的概念，采用實時不交化的研究方法，能夠有效降低網絡算法的復雜性。然而，對于邊權、點權和一般賦權三種不同賦權形式的網絡系統，RDA 算法的推導過程有所區別，實際計算時也需要對不同形式的網絡系統采用相應的算法程序，過程稍顯繁瑣。本章先對原RDA 算法的推導過程進行簡要介紹，在此基礎上，將其三部分程序整合化簡，發展出統一RDA 算法。最后，通過簡單算例，驗證統一RDA算法的正確性。

1.1 原RDA 算法簡介

一般來說，生命線工程系統的網絡分析模型是一個兩狀態關聯系統，即元件和系統只有安全和失效兩個狀態，用系統的結構函數φ(G)來表示，φ(G)=1 表示系統處于安全狀態，φ(G)=0則表示系統處于失效狀態。

1.1.1 邊權網絡系統

定義系統G=(V,E)中從一起始點到一終止點的所有最小路中路徑最短的一條為系統G=(V,E)安全的一個基本事件A1=a1,1a1,2···a1,m1，則系統的結構函數：

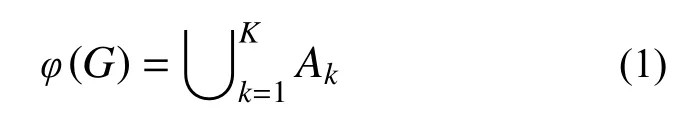
式中：Ak為系統的第k條最小路；K為系統的所有最小路數；a1,m1為A1中第m1條邊。

由布爾運算有：

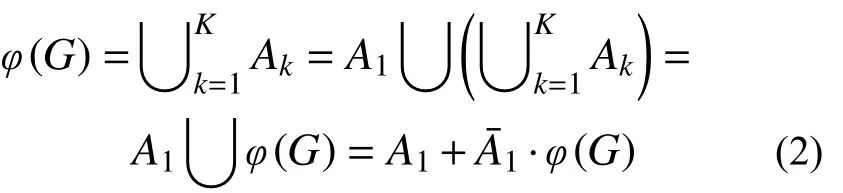
由互斥和公式：

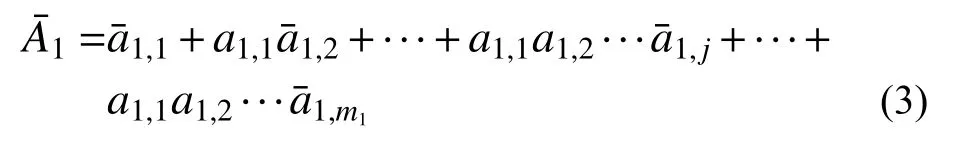
將式(3)代入式(2)中，由布爾簡化得到：

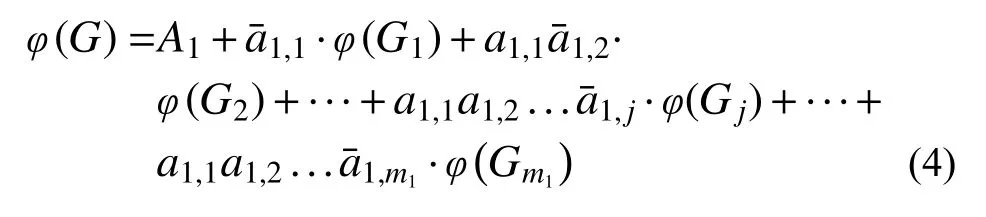
式中，Gi為從網絡系統G=(V,E) 中去掉邊a1,i后得到的網絡系統圖，即由a1,1a1,2···1,i決定的系統子圖。

繼續對各連通子圖分別尋找最短最小路，并按上述格式分解，運用布爾運算法則進行化簡與歸并，則在最終分解完畢，不再存在連通子圖時，有：

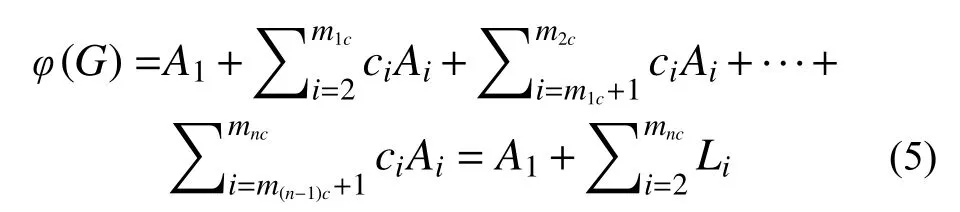
式中：ci為第i個連通子圖結構函數前的系數；Ai為 第i個 連 通 子 圖 的 一個最短最小路；mnc為系統所有連通子圖數；Li(i=2,3,···,mnc)為歸并運算后的不交最小路。

若令L1=A1，則式(5)可以寫為更為一般的形式：

1.1.2 點權網絡系統

點權網絡系統的RDA 算法與邊權網絡系統的推導過程大致相同，但在最小路的生成和遞推生成子系統圖時有所區別。RDA 算法采用寬度優先搜索生成系統或各子系統的最小路，此時的最小路為頂點最小路。在點權網路系統中，此時寬度優先搜索生成的最小路就是真實的點最小路，不需要再對其進行吸收歸并運算。

遞推分解生成點的不交最小路后，點權網絡系統可靠度為：

因此，點權網絡系統除了網絡系統可靠度和網絡失效概率表達式與邊權有所不同，其余均與邊權網絡系統一致。

1.1.3 一般賦權網絡系統

一般賦權網絡系統的RDA 算法比邊權和點權更為復雜。在一般賦權網絡系統中，頂點和邊可以同時存在失效狀態。網絡系統頂點的失效，將導致與此頂點相聯的邊失去連接功能，實際上相當于此頂點的相連邊也發生了失效；反過來，與一頂點相連的所有邊的失效也相當于此頂點的失效。反映在不交最小路和不交最小割上，頂點和邊的狀態為相依隨機事件,不交最小路和不交最小割事件的發生概率不能再采用元件失效獨立假定下的計算公式，而是需要計算相依隨機事件的聯合失效概率。

一般賦權網絡系統的RDA 算法采用了Torrieri[19]在1994 年提出的一種計算一般賦權有向網絡系統不交最小路發生概率的方法，該方法把頂點可靠度嵌入邊中，使一般賦權有向網絡系統等價變換為獨立失效的邊權網絡系統，通過計算獨立失效邊權有向網絡系統不交邊最小路的發生概率，得到一般賦權有向網絡系統不交最小路的發生概率，從而避免了聯合失效概率的計算。

因此，對于一個一般賦權網絡系統，先采用獨立邊權網絡系統的遞推分解算法找到所有的不交最小路和不交最小割，再對于每一條不交最小路和不交最小割，用Torrieri 提出的方法計算發生概率，最后得到系統可靠度，具體過程如下。

1.2 統一RDA 算法

原RDA 算法的推導過程表明：系統的結構函數不必通過求出系統所有最小路來建立，而是可以通過系統的一個最小路分解，來遞推下一個互斥最小路，并且由過程中產生的不連通子圖，可以給出互補結構函數，從而利用概率不等式計算給出的系統可靠度的上、下界，實時估計系統連通可靠度的近似值。進一步地，結合計算機編程，可以大幅降低大型網絡系統可靠度計算的復雜性。

生命線工程網絡系統存在單向邊和雙向邊，區別在于該邊的兩個頂點是否有向。在網絡圖建模時，以鄰接向量矩陣作為網絡圖的存貯方式，將雙向邊拆分成兩條單向邊，此時單向邊或雙向邊就可以在鄰接向量矩陣中進行區分。

由于三種賦權形式的網絡系統的RDA 算法推導過程有所不同，原RDA 算法的計算程序也分成三部分，在計算時，三種賦權形式的網絡系統需要輸入的條件也不同：邊權網絡系統由于頂點永遠安全，默認各頂點失效概率為0，只需要輸入各邊可靠度以及網絡的鄰接向量矩陣；同理，點權網絡系統默認各邊失效概率為0，只需要輸入各節點可靠度以及網絡的鄰接向量矩陣；一般賦權網絡系統則需要輸入各邊可靠度、各節點可靠度以及網絡的鄰接向量矩陣。

為了簡化實際運用中的計算過程，希望將三部分程序合為一個。根據三種賦權形式網絡的特點，本文在原RDA 算法的基礎上，發展出統一RDA 算法。

以一般賦權網絡系統的RDA 算法程序為載體，將邊權和點權的計算程序歸并入一般賦權程序中，操作方法如下：在計算邊權網絡系統可靠度時，采用一般賦權程序，其中各邊可靠度和網絡鄰接向量矩陣的輸入與邊權的輸入相同，各節點可靠度均取為1，表示此時各節點是絕對安全的，這樣也符合邊權系統的定義。同理，用一般賦權程序計算點權系統時，各節點可靠度和網絡鄰接向量矩陣的輸入與點權的輸入相同，各邊可靠度均取為1。

1.3 算例驗證

為了驗證統一RDA 算法的正確性，采用下圖1所示網絡，分別計算邊權程序、點權程序和一般賦權程序退化的邊權、點權系統的可靠度結果，見表1，對比驗證。

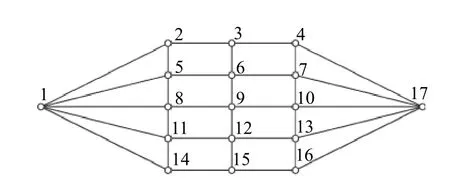
圖1 17 節點網絡結構圖Fig.1 17-node network structure

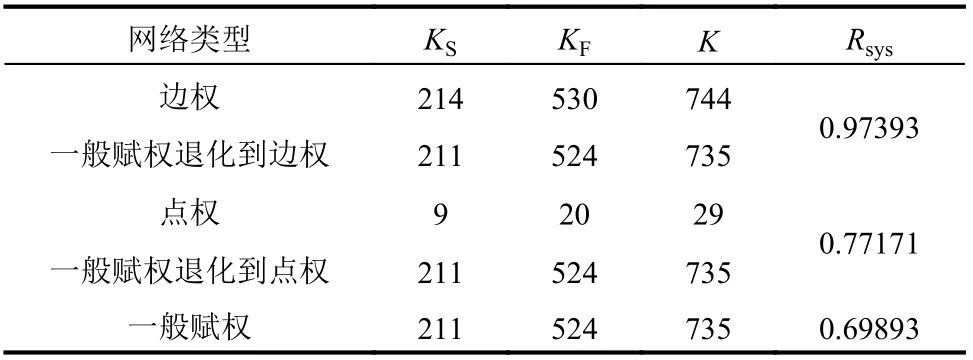
表1 17 節點網絡可靠度計算結果Table 1 Reliability calculation results of 17-node network system

該系統有17 個節點，32 條邊，系統的源點和終點分別為1 和17，邊或節點的可靠度均取為0.9。

程序計算結果表明：由統一RDA 算法退化的邊權、點權與原邊權、點權算得的可靠度結果完全一致，但不交最小路數與不交最小割數不同，而與一般賦權一致。其中，統一RDA 算法退化的點權算得的不交最小路數與不交最小割數與原點權算法相差較大，而統一RDA 算法退化的邊權算得的不交最小路數與不交最小割數與原邊權算法相近，統一RDA 算法的計算量略有增大。

綜上所述，原RDA 算法以邊權網絡系統為主要研究對象，進行了詳細的遞推分解過程的推導，給出完整的可用于計算邊權網絡系統可靠度的算法。而點權網絡系統和一般賦權網絡系統的RDA 算法均以邊權網絡系統為基礎，結合自身特點略有改動。而由于三種賦權形式網絡系統RDA算法的區別，與之對應的計算程序也分成三個。為了簡化計算過程，以一般賦權網絡系統的RDA算法程序為載體，將邊權和點權的計算程序歸并入一般賦權程序中，又將三部分整合為一體，發展出統一RDA 算法，不僅使用更加方便，也使RDA 算法程序更加完整緊湊。

2 相依失效工程網絡系統抗震可靠度估計的RDA 算法

在同一震源下，由于生命線工程結構各設備間往往存在相互連接的關系，因此實際上工程網絡系統是失效相關的。本章研究相依失效工程網絡系統抗震可靠度的估計問題，在統一RDA 算法的基礎上，實際上就是研究不交最小路和不交最小割的聯合概率計算問題，其求解過程包含系統元件(結構)極值響應邊緣分布模型估計[20?21]和極值響應聯合分布模型估計兩部分。

為了有效解決不交最小路(割)的聯合概率計算問題，本文先引入移位廣義對數正態分布(Shifted Generalized Lognormal Distribution，簡稱SGLD)模型建立結構荷載效應的邊緣分布函數，再分別采用SCM 和Gumbel Copula，建立結構荷載效應的聯合分布函數，計算聯合失效概率。最后，將算得的不交最小路和不交最小割的聯合概率嵌入統一RDA 算法，從而有效估計相依失效生命線工程網絡系統的可靠度。

2.1 基于SGLD 模型的邊緣分布函數

SGLD 是一種四階矩概率模型，不僅具有確定的概率密度函數表達式和累積分布函數表達式，而且具備較廣的偏態系數-峰度系數空間[22]，因此，可用來模擬大多數的函數類型。基于SGLD模型，可給出地震作用下結構響應邊緣分布的尾部估計。

SGLD 的累積分布函數的理論表達式為：

2.2 基于SCM 的不交最小路(割)的聯合概率計算

SCM 是多維正態分布的一種新的計算方法，其基本思想是把N維正態分布函數看成由N個具有邏輯關系的事件組成的系統的可靠概率，通過依次把兩個具有邏輯關系的事件組合成一個復合事件，最終將整個系統復合成一個總事件，通過總復合事件的可靠度指標來計算多維正態分布的聯合概率函數值。

SCM 的計算步驟如下：

2.3 基于Gumbel Copula 的不交最小路(割)的聯合概率計算

本文采用單一參數多變量Gumbel Copula，主要需要估計其參數θ。基于兩水準方法估計參數時的反應樣本，由矩方法的基本思想，讓基于樣本的Kendall’s tau 和基于總體的Kendall’s tau 相等，先得到等級相關系數Kendall’s tau，進而再計算得到參數θ。

對于n維Gumbel CopulaCθ(u)，u=(u1,u2,···,un)，其樣本一致性系數Kendall’s tau 的計算公式為：

2.4 相依失效生命線工程系統抗震可靠度估計的統一RDA 算法

對于相依失效生命線工程系統的可靠度估計問題，先由統一RDA 算法找到所有的不交最小路和不交最小割，再對于每一條不交最小路和不交最小割，考慮相依失效，采用SCM 或Gumbel Copula計算聯合失效概率，最后回到統一RDA 算法，估計整個系統的抗震可靠度。同時，結合本文第二章，此方法也可退化應用于相依失效的邊權網絡系統和點權網絡系統。

因此，本文的方法可用于三種賦權形式的相依失效工程網絡系統的抗震可靠度估計，使用范圍廣，精確度高，具有廣闊的應用前景。

3 算例分析

在各類生命線工程系統中，區域電力系統結構的地震破壞分析具有代表性。相對于電力系統中的工程結構和高壓電器設備而言，輸電線路的地震破壞較輕，因此，當不考慮電力系統中輸電線路的地震失效時，電力系統被認為是一個點權系統。如果把電力系統中某一結構或設備作為源點，另一結構或設備作為終點，那么由源點到終點的整個系統就構成了一個拓撲網絡，其中各個結構或設備作為網絡的節點，輸電線路作為網絡的邊。

本章以一假想電力系統為例，將其簡化為下圖2 所示的36 節點格柵型網絡，采用第二章提出的算法，估計該網絡系統相依失效的動力抗震可靠度。先建立系統的動力學模型，利用SGLD 模型建立結構的邊緣分布函數，估計元件單體的可靠度。再由元件失效相依，分別采用SCM 和Gumbel Copula，建立結構的聯合分布函數，計算聯合失效概率。最后，采用統一RDA 算法，得到系統的抗震動力可靠度估計結果。

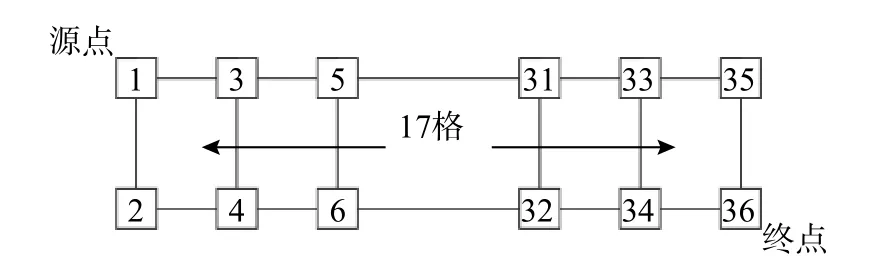
圖2 格柵型網絡結構示意圖Fig.2 Schematic diagram of grid network structure

本文采用的相依失效生命線工程系統抗震可靠度估計的統一RDA 算法，不僅可以系統性地考慮網絡系統結構相依失效的情況，還能在保證精度的前提下大大減少計算量，充分體現該方法的有效性。

3.1 地震作用下的系統動力學模型

要進行36 節點網絡系統相依失效下的抗震可靠度評估研究，必須先建立系統的動力學模型，計算各元件單體的隨機地震響應。由于動力相互作用的存在，有限元分析中的模型變得十分復雜，計算費時費力，不適用于大量的研究分析工作中。

假設圖2 所示包含36 個設備的電力系統，同一列的兩個節點(如節點1 和2，節點3 和4)由硬母線或帶滑移接頭的軟母線連接，因此，需要考慮動力相互作用，而橫排連接母線為一般柔性母線，不引起動力相互作用。

為了簡化電力系統中設備的非線性隨機地震動分析計算復雜的問題，美國學者Der Kiureghian[24?25]在1999 年最早提出了基于單自由度設備模型的理想化系統簡化方法，建立了系統的動力學模型。該方法的基本思路是：用一個假設的位移形函數描述設備的變形，那么每個設備將會被簡化成一個單自由度振子，這個振子的有效質量、有效剛度、有效阻尼以及外部慣性力均與原設備對應。由硬母線或帶滑移接頭軟母線連接的兩個設備則被理想化為一個雙自由度系統，各參數仍與設備自身特性以及連接母線的特性相對應，理想化模型示意圖見圖3。

圖3 相連設備的理想化動力學模型[26]Fig.3 Idealized dynamic model of connected equipment[26]

隨機地震作用下，兩設備間的連接母線進行非線性隨機振動。考慮動力相互作用，在雙自由度系統內建立母線的滯回回復力模型。

以i、j表示兩個存在相互作用的設備，具體公式如下：

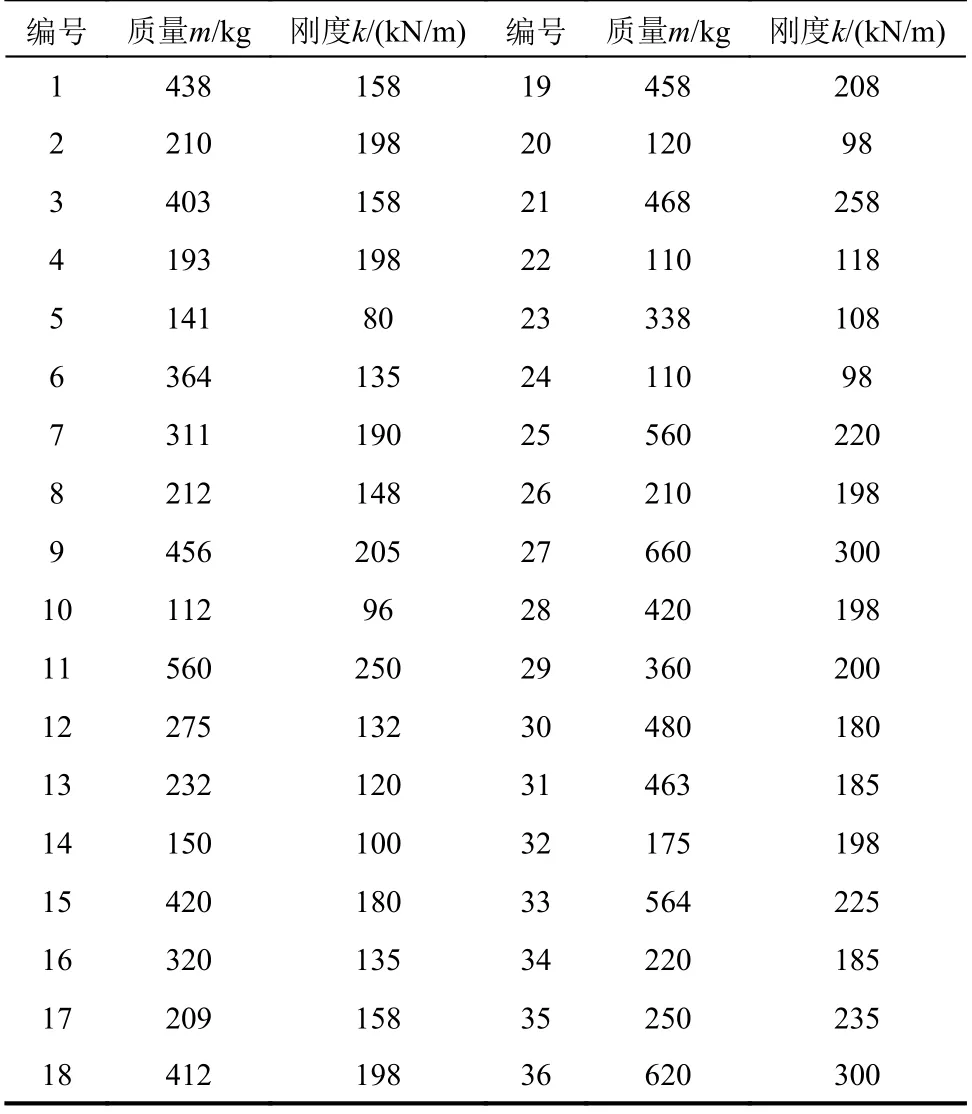
表2 電器設備的有效質量和剛度Table 2 Values of effective mass and stiffnessof equipment items

本節建立系統的動力學模型，用于計算電力系統內各單元的隨機地震響應，由響應樣本估計單體的邊緣分布和系統的聯合分布，最終基于RDA算法可得到該電力系統相依失效的動力抗震可靠度。

3.2 結構響應隨機樣本生成

本文利用Mathematica10.0 程序進行編程計算，為了保證計算精度，隨機抽樣生成2000 個地震激勵樣本，作用于該36 節點網絡結構上，將結構同一格的兩個節點理想化為一個雙自由度系統，得到36 個節點在地震動作用下的2000 組隨機響應數據樣本。圖4 為3 組地面地震動加速度時程樣本曲線，圖5 為這3 組地震輸入下，節點1 對應的響應曲線。利用這2000 組響應樣本，先通過SGLD 模型估計結構隨機響應的邊緣分布，再利用SCM 和Gumbel Copula 函數分別計算聯合失效概率，即可得到該結構相依失效下的結構系統抗震可靠度。

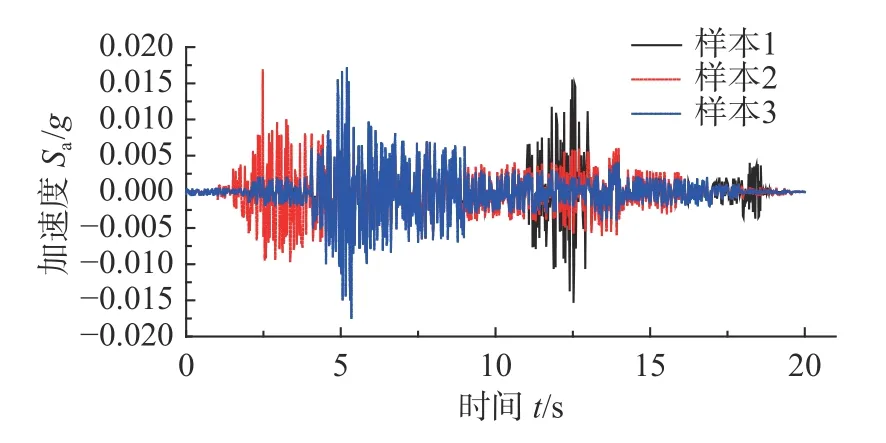
圖4 地震譜樣本曲線Fig.4 Sample curves of seismic spectra

圖5 節點1 對應的隨機響應曲線Fig.5 Random response curves corresponding to Node 1

3.3 結構體系邊緣分布分析

基于2000 組隨機響應樣本，本節分別采用矩方法和兩水準方法，先識別出SGLD 模型的模型參數，結果列于表3 中，再由模型參數，得到結構體系響應尾部分布的近似值。兩水準方法對應的兩個控制點分別取為P1=0.1、P2=0.05。圖6 為其中兩個節點的超越概率曲線圖，橫軸表示變量X的限值，縱軸表示當X取不同限值時，滿足該分布函數的結構響應的超越概率Pf。

圖6 表明：矩方法和兩水準方法計算得到的超越概率吻合度較高。在分布的中后段，兩種方法給出的超越概率結果幾乎一致。因此，可以認為基于兩水準方法的SGLD 模型能夠用于本結構響應分布的尾部估計，且效率較高。

3.4 結構體系的聯合概率計算和系統可靠度計算

本節基于2000 組隨機響應樣本，分別采用SCM 和Gumbel Copula 計算不交最小路和不交最小割的聯合概率，再將聯合概率計算結果嵌入統一RDA 算法，即可算得系統的抗震可靠度。

SCM 需要計算2000 組響應樣本的相關系數和各元件的可靠度指標，再依次把兩個事件組合成一個復合事件，最終將整個系統復合成一個總事件，通過總復合事件的可靠度指標來計算多維正態分布的聯合概率函數值。而Gumbel Copula 需要計算Kendall’s tau 和模型參數θ，結合邊緣分布結果來建立Copula 函數。算得聯合概率后，將結果嵌套進統一RDA 算法，即可得到結構系統的相依失效可靠度。

由2000 組樣本數據算得的相關系數為36 階對稱矩陣，因數據較多，此處僅列出前6 個節點之間的相關系數矩陣，見表4。算得的Gumbel Copula 所需的τ=0.005185， θ=1.0694。結構系統的可靠度計算結果見表5。

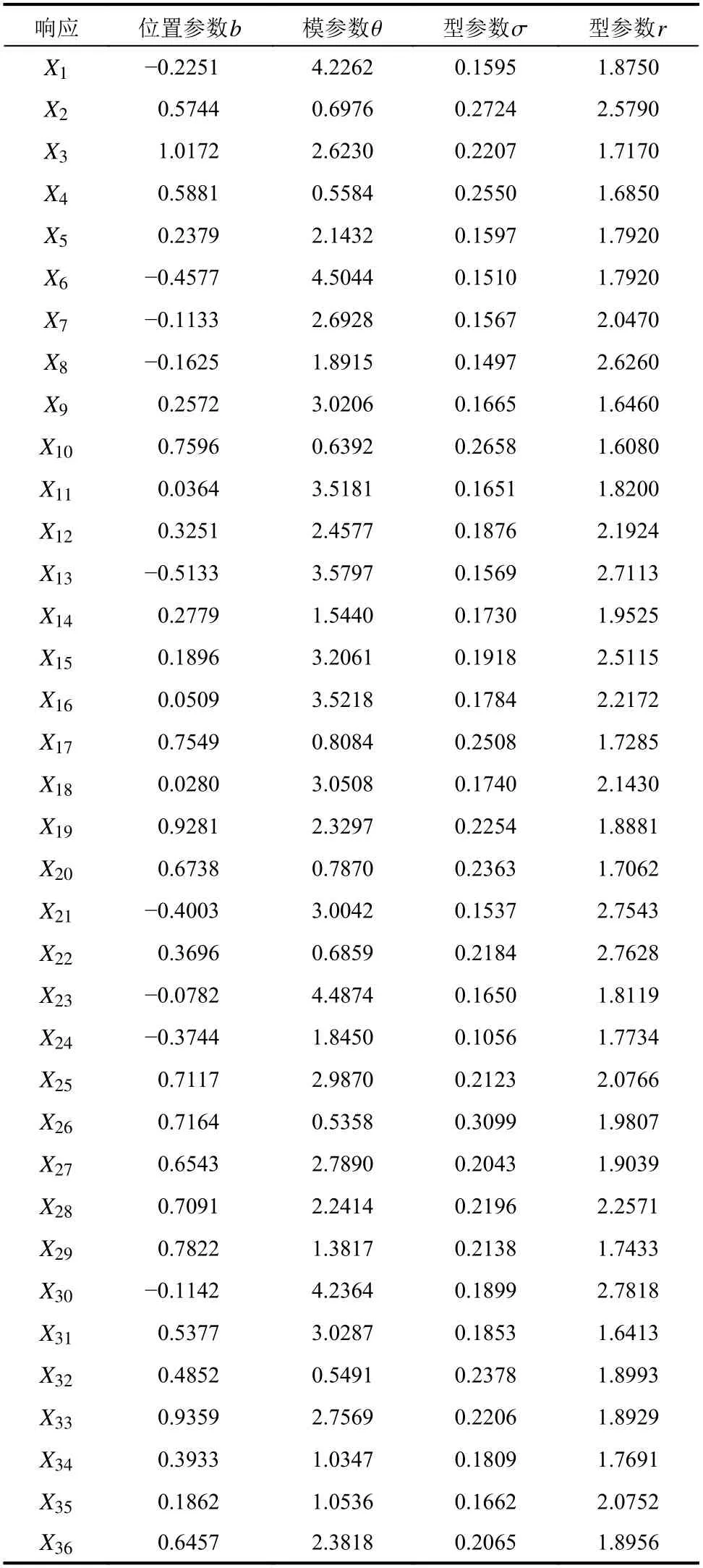
表3 SGLD 模型參數Table 3 SGLD model parameters

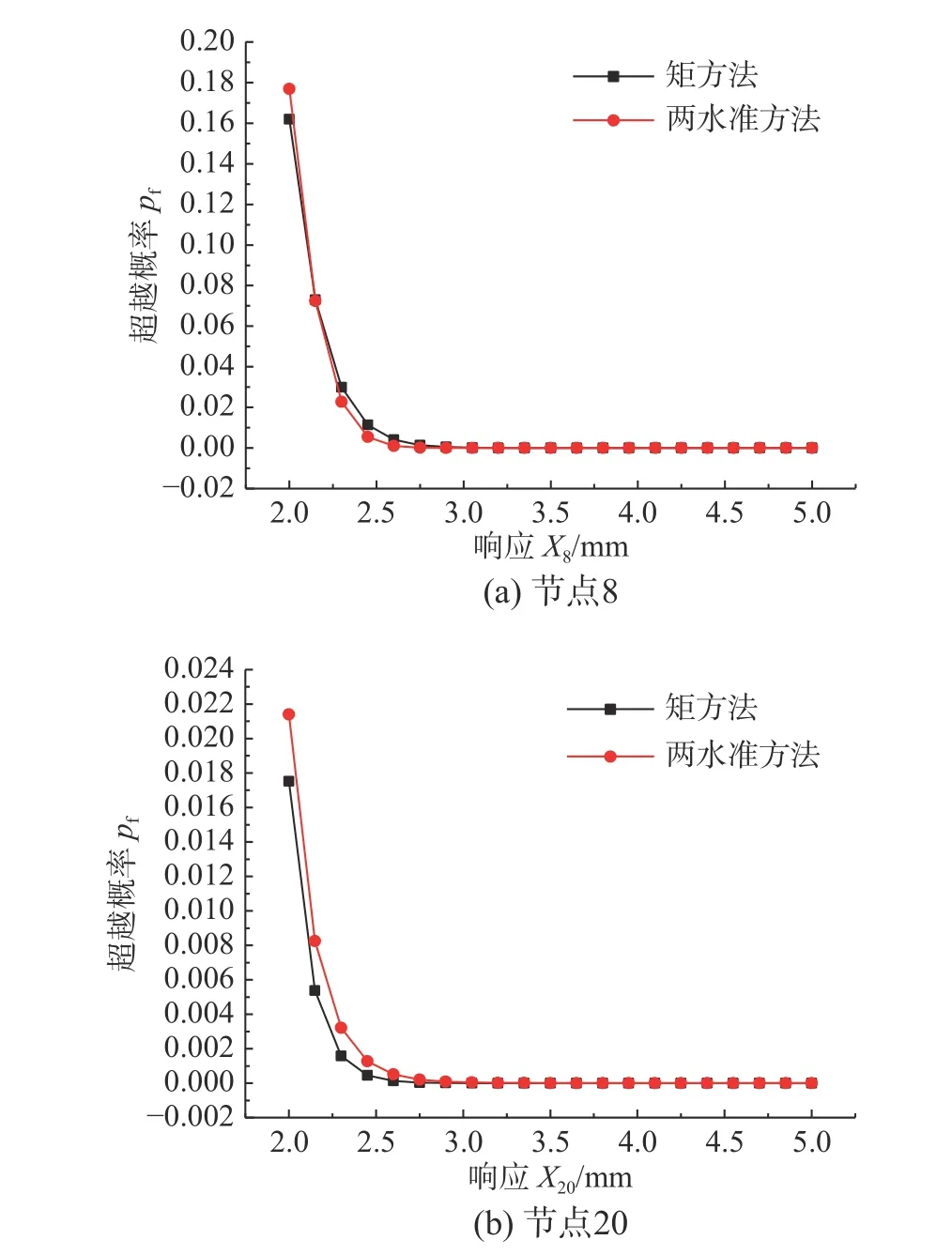
圖6 各構件結構響應的超越概率曲線圖Fig.6 Exceedance probability curves of structural response of each component

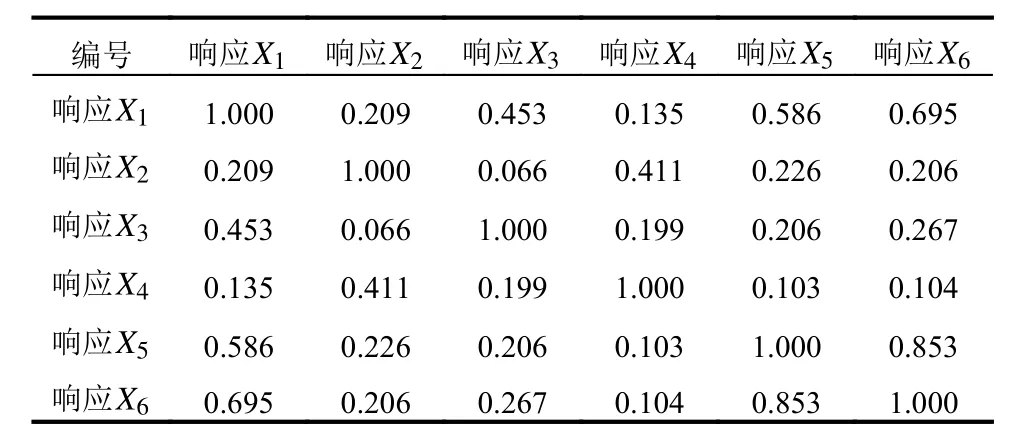
表4 局部相關系數矩陣Table 4 Local correlation coefficient matrix

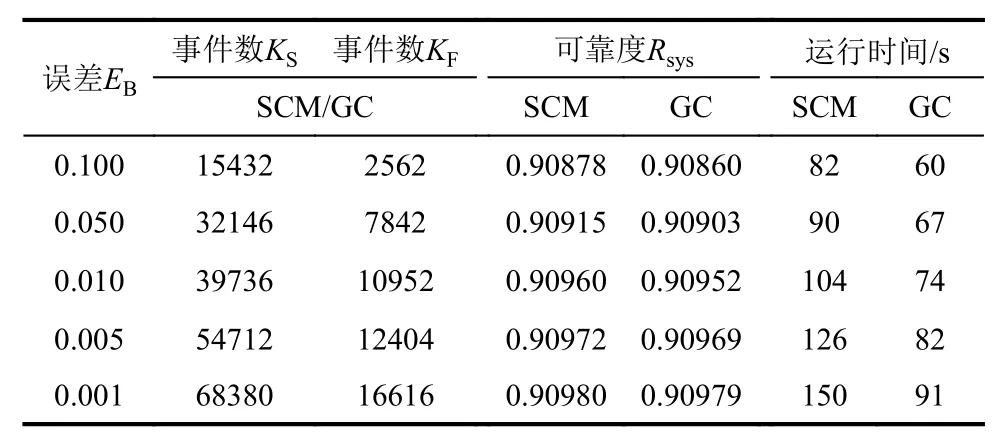
表5 36 節點結構網絡系統可靠度計算結果Table 5 Reliability calculation results of 36-node network system

圖7 為以Gumbel Copula 可靠度計算結果為基準的相對誤差變化曲線，橫坐標為RDA 算法中設定的誤差限值，縱坐標為兩種方法可靠度計算結果的相對誤差。

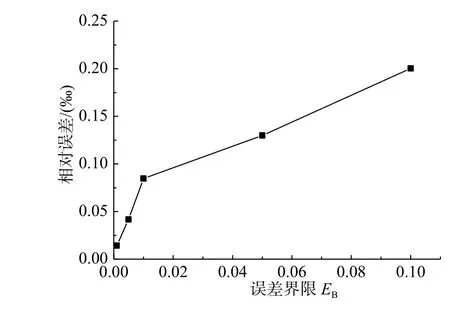
圖7 兩種方法可靠度計算結果的相對誤差Fig.7 Relative error of reliability calculation results of two methods

以上結果表明：一方面，隨著設定誤差界限的降低，RDA 算法需要計算的不交最小路、不交最小割以及計算時間都在變多，但仍遠小于傳統遞推分解法，體現了本文計算方法的優勢；另一方面，在相同的誤差限值下，SCM 和Gumbel Copula 兩種方法的計算事件數完全一致，這是因為不交最小路和不交最小割數均是由RDA 算法確定。兩種方法的結構可靠概率計算結果非常接近，以Gumbel Copula 為基準的最大相對誤差不超過0.2‰，但在誤差限值較大的區域出現較大偏差。同等條件下，Gumbel Copula 的計算時間要低于SCM，且計算過程更為簡潔。

3.5 統一RDA 算法的正確性驗證

當不考慮電力系統中輸電線路的地震失效時，本章36 節點電力系統被認為是一個點權系統，表5 為由統一RDA 算法退化計算的點權網絡系統的抗震可靠度結果。本節將用SCM 和Gumbel Copula 計算的不交最小路和不交最小割的聯合概率嵌入點權的RDA 算法，再次驗證統一RDA 算法的正確性，計算結果見表6。

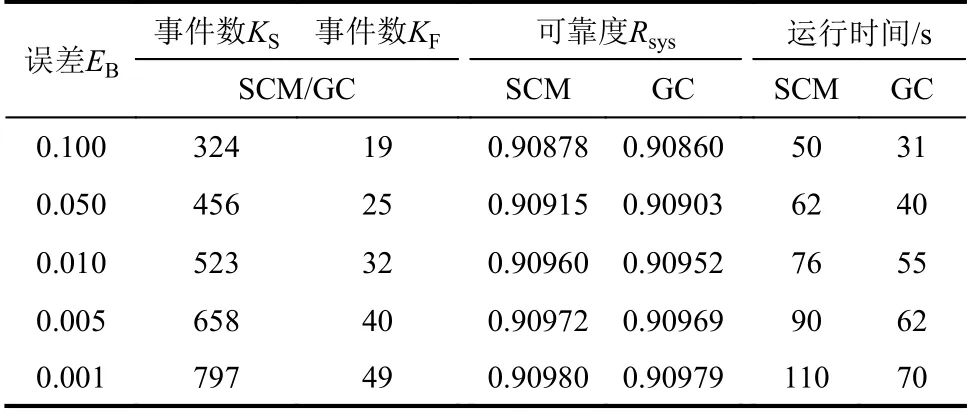
表6 點權網絡系統的可靠度計算結果Table 6 Reliability calculation results of node weight network system

計算結果驗證了統一RDA 算法的正確性，但該網絡結構由統一算法退化到點權的不交最小路和不交最小割數遠大于原點權算法，計算量增加。

結合圖1、圖2 兩個網絡的可靠度計算結果，當網絡系統中節點少、邊多，兩者數量相差較大，網絡結構比較復雜時，統一RDA 算法實用性較高；而當網絡系統中節點數與邊數比較接近，網絡結構比較簡單時，統一RDA 算法的計算量可能會大大增加，從而導致計算費用增加，不適合應用于工程實踐。因此，統一RDA 算法研究的意義主要在于理論簡化，并以此為基礎進一步進行相依失效情況下的生命線工程系統抗震可靠度估計研究。

綜上所述，雖然統一RDA 算法根據不同的網絡系統結構，使用有一定的局限性，但其將原RDA算法整合成一個程序，并且基于統一RDA 算法發展出的相依失效生命線工程系統抗震可靠度估計的統一RDA 算法，不僅可以較好地考慮元件相依失效，而且可以退化到邊權和點權。對于統一RDA 算法計算量增加的問題，計劃后續將做更深入的研究，對統一RDA 算法中的不交最小路和不交最小割進行歸并，從而減小不交最小路數和不交最小割數，降低計算量。本文的方法為以后的研究奠定了良好的理論基礎，希望通過進一步的研究改進，能夠將其更好地應用于工程實踐中。

4 結論

本文先對原RDA 算法三部分程序進行整合簡化，發展出統一RDA 算法，再在統一RDA 算法的基礎上，引入SCM 和Gumbel Copula 函數兩種方法，分別計算RDA 算法中不交最小路和不交最小割事件的聯合失效概率，最后發展出相依失效生命線工程系統抗震可靠度估計的統一RDA 算法，較好地解決了生命線工程系統中元件失效相關的可靠度估計問題。算例計算結果表明：該方法在保證計算精度的前提下，可以用于相依失效生命線網絡系統的抗震可靠度評估。

本文的主要研究結論有：

(1)相依失效生命線工程系統抗震可靠度估計的統一RDA 算法不僅可以較好地考慮元件相依失效，而且可以退化到邊權和點權，具有良好的適用性；

(2) SCM 和Gumbel Copula 可以用于結構體系可靠度估計中的聯合概率計算。相比之下，Gumbel Copula 計算過程更加簡潔，計算效率更高；

(3)本文方法適用于大多數的生命線工程系統抗震可靠度的估計，對于統一RDA 算法退化到邊權、點權計算量增加的問題，后續將做進一步的研究。