平面曲梁面外自由振動有限元分析的p 型超收斂算法

葉康生，梁 童

(清華大學土木工程系，土木工程安全與耐久教育部重點實驗室，北京 100084)

平面曲梁結構在現代土木、航天、機械等領域具有廣泛的應用，其自由振動是結構分析的重要內容。該問題目前的分析方法主要有：有限元法[1?3]、有限差分法[4]、微分容積法[5?6]、偽譜法[7]、動力剛度法[8?10]等，其中有限元法應用最為廣泛。

有限元法求解自由振動問題時，計算精度由單元次數和網格劃分決定。網格越密，單元次數越高，計算精度越好，但計算量亦隨之大幅攀升，高階頻率和振型尤甚[1]。因此，研究如何有效提高有限元求解自由振動問題的精度和效率具有十分重要的意義，超收斂計算則是解決這一難題的有效途徑。

目前結構自由振動問題的各類有限元超收斂求解方法，基本都是先對振型進行超收斂修復，再將修復后的振型代入Rayleigh 商得到頻率的超收斂解，區別主要在于對振型的超收斂修復做法不同。這些方法中最典型的是文獻[11]提出的SPRD法，該法利用振型結點位移的超收斂性，在多個單元組成的小片上通過對振型用更高次多項式對結點位移進行多項式擬合獲得振型的超收斂解。文獻[12]的做法與文獻[11]做法類似，亦是基于振型結點位移的超收斂性，在幾個單元構成的小片上通過對振型用更高次多項式對結點位移作多項式插值獲得振型的超收斂解；文獻[13?14]僅修復振型所對應的應力，并代入Rayleigh 商的應變能部分，通過應變能計算精度的提高獲得頻率的超收斂解；文獻[15?16]利用等幾何分析法，通過構造高階質量矩陣，獲得頻率的高精度解；另外還有文獻[17]基于外推的方法和文獻[18]基于投影的方法。

文獻[19]對自由振動問題提出一種p型超收斂算法，結果顯示，該法簡單、高效，能顯著提升頻率和振型的精度和收斂階。文獻[20]將該法應用于平面曲梁的靜力分析中，文獻[21]將該法延拓至平面曲梁的面內自由振動分析中，文獻[22]將該法延拓至歐拉梁的彈性穩定分析中，文獻[23]將該法延拓至非線性常微分方程邊值問題的分析中。本文的工作是文獻[19?23]工作的延續，是文獻[21]工作的后半部分，進一步將p型超收斂算法應用于平面曲梁的面外自由振動分析中。數值算例表明，該法仍延續了求解前述問題時的優秀表現，算法穩定、高效，能顯著提高解答的精度、質量和收斂階，再次展現了p型超收斂算法在求解自由振動問題時的優良特性。

1 平面曲梁自由振動分析模型

平面曲梁的軸線為平面曲線，所有截面關于軸線所在平面對稱。如圖1 所示，建立曲梁分析的xyz坐標系，x、y分別沿軸線切向、法向，z垂直于軸線所在平面。記s為軸線弧長坐標。曲梁面外自由振動時，分別記面外位移、y軸轉角位移和扭轉角位移為w(s) 、 θ(s) 、 ?(s) ，對應內力Q、M、T如圖1 所示。

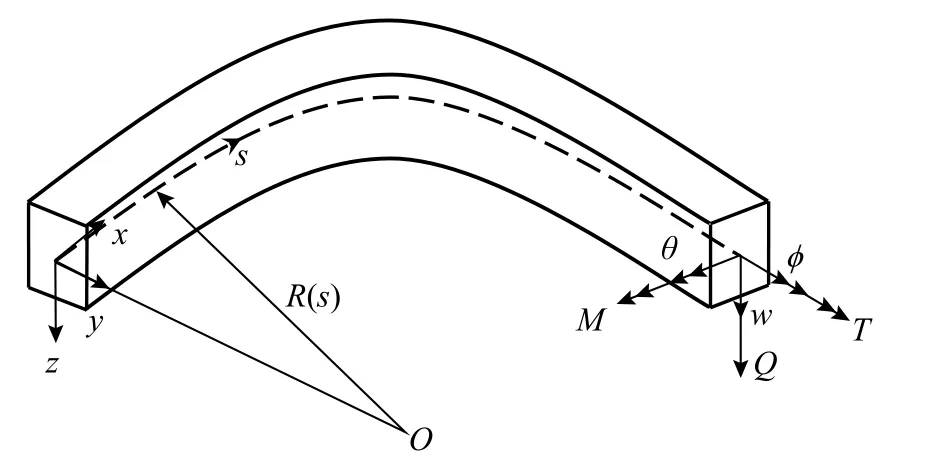
圖1 平面曲梁Fig.1 Planar curved beam

面外自由振動時，曲梁的幾何方程、物理方程和平衡方程分別為[24]：

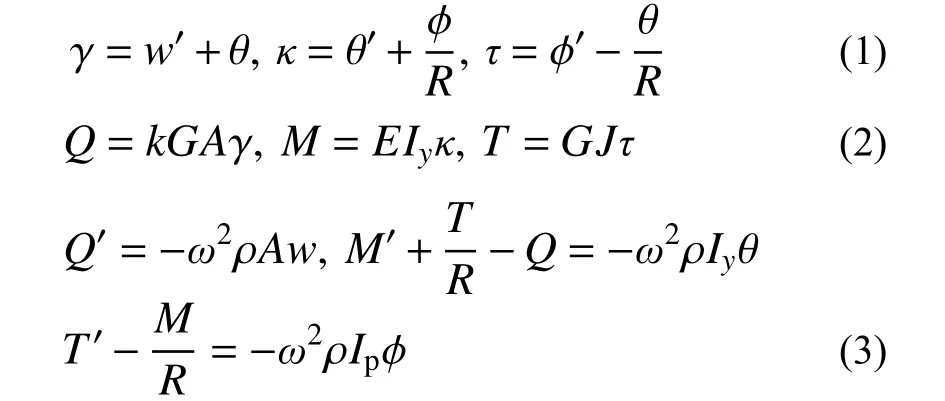
式中： ()′=d()/ds；E為彈性模量；G為剪切模量； ρ為材料密度；A為截面面積；Iy為截面關于y軸的慣性矩；Ip為截面極慣性矩；k為截面形狀系數；J為截面扭轉常數；R為軸線曲率半徑，當軸線曲率中心位于y軸正向時R為正，位于y軸負向時R為負。

將物理方程和幾何方程代入平衡方程，得到用位移表示的平面曲梁面外自由振動的控制微分方程為：

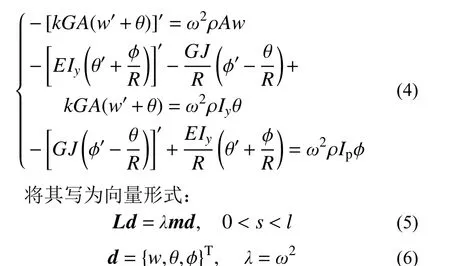
式中：l為曲梁的軸線長度；L、m為相應的微分算子矩陣，其具體表達式可由式(4)導出，此處不再詳細給出。該問題理論上有無窮多組解答(λn,dn(s)),n=1,2,··· ，特征值λn按從小到大排序：

用有限元法求解該問題時，先對結構進行有限元離散，將結構劃分為ne個單元，如圖2 所示。

記網格尺寸：

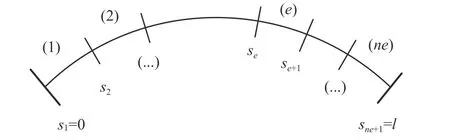
圖2 有限元網格劃分Fig.2 Finite element mesh

式中，he為單元 (e) 的軸線長度，he=se+1?se。雖然理論上d={w,θ,?}T中三個位移分量的形函數階數可取為不同，但數值結果表明，有限元解的收斂階取決于這三個位移分量形函數階數中的最低值，為使有限元自由度的求解效率得到充分發揮，應讓三個位移分量的形函數階數取為相同，故本文有限元計算和超收斂計算中三個位移分量的形函數階數均取為相同。在任意單元 (e)內，采用m次Hierarchical 形函數將解答近似為：

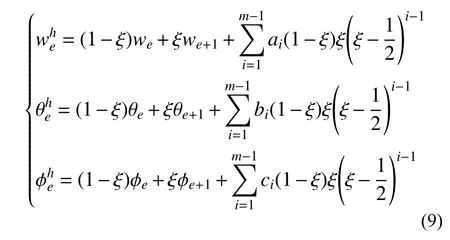
式中： ξ=(s?se)/he，為單元 (e)上的無量綱坐標；we、 θe、 ?e為第e個結點上的結點位移；ai、bi、ci(i=1,2,···,m?1) 分別為w、 θ 、 ?的單元內部自由度。將式(9)寫成矩陣形式：

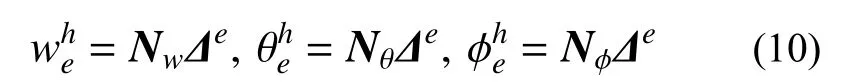
式中， ?e為單元 (e)的自由度向量，具體為：

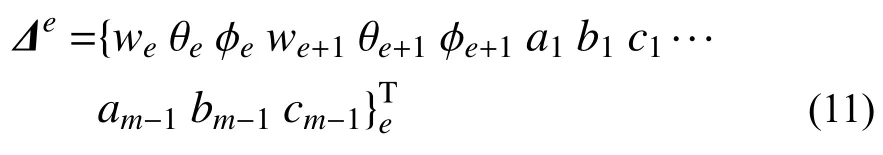
Nw、Nθ、N?分別為w、 θ 、 ?的形函數矩陣，其具體表達式可由式(9)和式(11)導出。

由變分原理[1]，有限元法將原問題離散為如下矩陣廣義特征值問題：

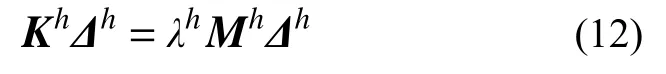
式中：Kh和Mh分別為該網格下的整體剛度矩陣和整體質量矩陣，分別由單元剛度矩陣和單元質量矩陣集成獲得； ?h為該網格下的結構整體自由度向量。單元剛度矩陣和單元質量矩陣具體計算如下：

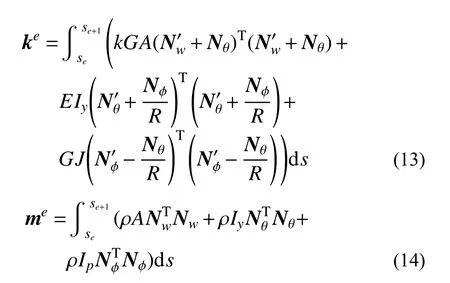
求解上述矩陣廣義特征值問題即可獲得該網格下的有限元解 (λhn,dnh(s))，n=1,2,···。

對該向量型常微分方程特征值問題，文獻[1]估計有限元解中頻率和振型分別具有如下收斂階：

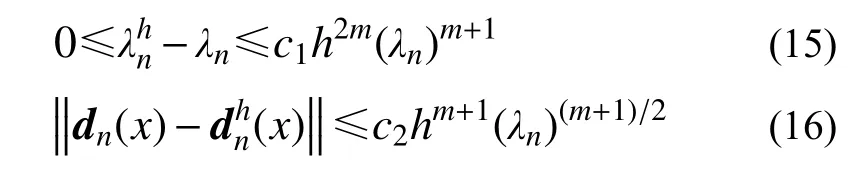
式中，m為單元多項式次數。

文獻[25]對該向量型問題對應的靜力問題Ld=f只有一個分量的最簡單情形，證明當采用m次元求解時，結點位移具有h2m階的超收斂性。數值算例表明，該結論對特征值問題同樣成立，在自由振動問題中，振型結點位移同樣具有h2m階的超收斂性，即：

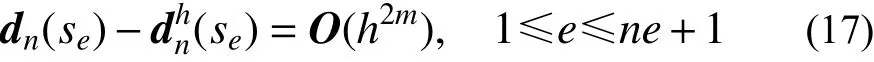
振型結點位移的超收斂性是本文算法的基礎。

2 超收斂求解思路

由式(5)可知，在單元 (e) 上，第n階振型dn(s)滿足如下常微分方程邊值問題：

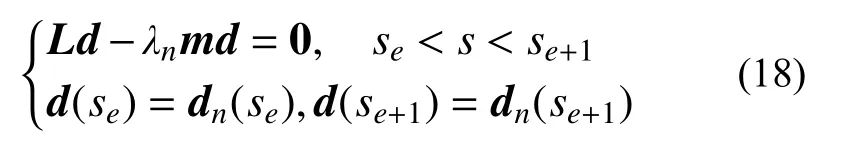
且當網格足夠密時，為該邊值問題的唯一解。

由式(15)和式(17)知，頻率和振型結點位移均具有h2m階的超收斂性。故在網格加密過程中，這些值將比內點位移更快地向精確解收斂，當網格足夠密時，有：

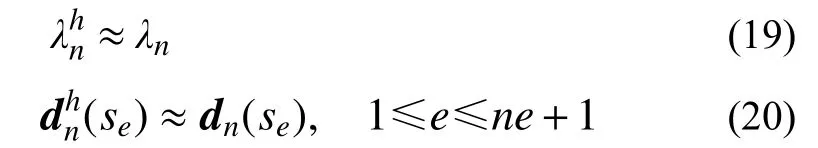
此時，單元 (e)上的振型將近似于下列線性邊值問題的解：

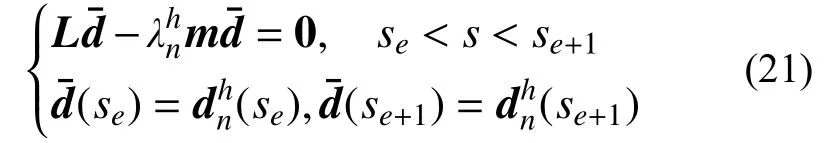
3 誤差估計

4 數值算例

本文算法已編成Fortran 程序。下面通過3 個數值算例來展示本文算法的計算精度和修復效果。為簡單起見，三個算例均采用無量綱計算。為考察振型收斂階，本文選取振型誤差向量模為長度的最大模：

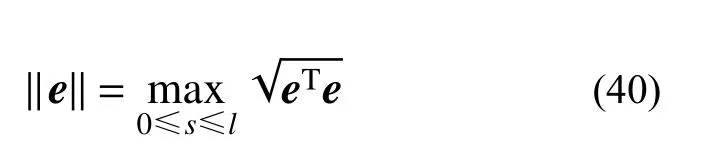
平面曲梁面外自由振動問題只有常截面圓弧曲梁具有解析解。為展現本文算法對收斂階的提升，例1 和例2 選取了不同邊界條件的兩個常截面圓弧曲梁；為展現本文算法的修復效果，例3 與已有文獻的計算結果進行了對比。

例1. 常截面圓弧曲梁1

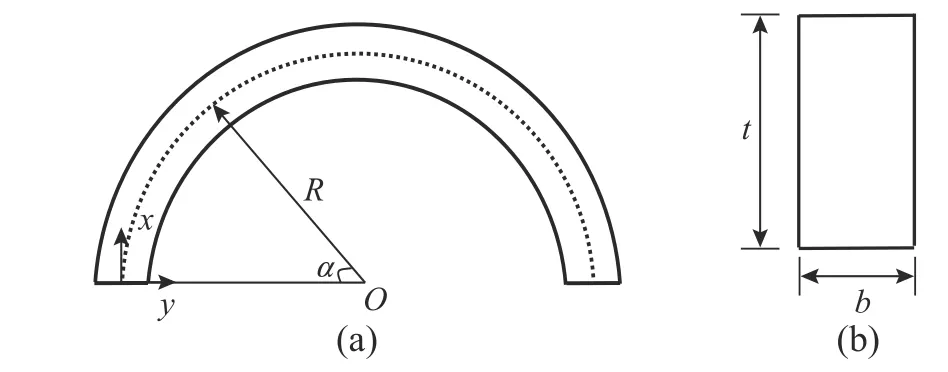
圖3 例1 常截面圓弧曲梁Fig.3 Uniform arch beam in Example 1

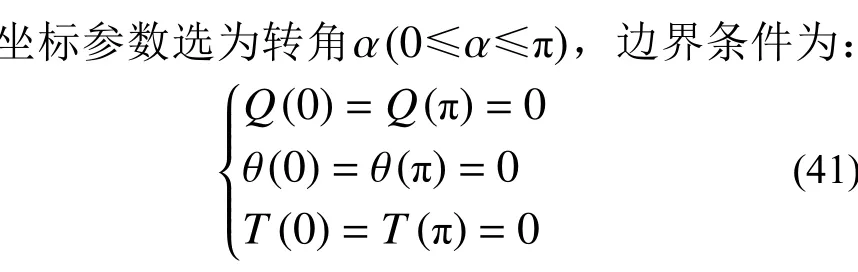
可求出該圓弧曲梁頻率和振型的精確解，根據文獻[26]，設其振型為：

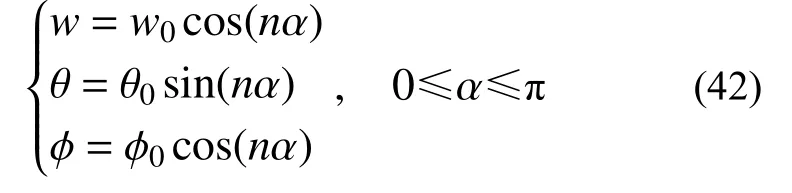
式中，n≥0且為整數。將式(42)代入式(4)，化簡可得關于 {w0,θ0,?0}T的齊次方程組。由于振型存在非零解，故該齊次方程組的系數矩陣奇異，其行列式值為零，從而可推出如下的頻率方程：

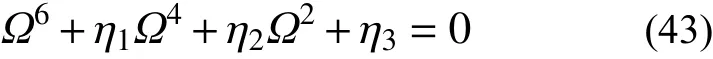
由該頻率方程可求出每個n值對應的三個頻率值。本例第一階、第二階頻率均為0，故對第三階頻率求解。第三階頻率對應n=2，頻率方程如式(44)所示，求解該方程可得如式(45)所示頻率。將求出的頻率代入 {w0,θ0,?0}T的齊次方程組，可求得對應的振型，如式(46)所示，該階振型取w(α=0)=1進行歸一化。

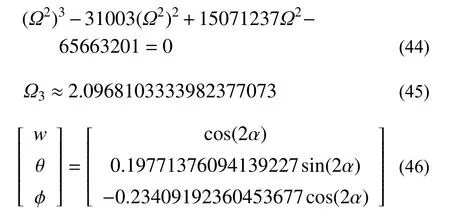
首先考察頻率、振型和振型結點位移有限元解的超收斂性。對該階振型分別采用二次元(m=2) 、三次元 (m=3) 和四次元 (m=4)進行有限元求解，計算頻率誤差 |???h|， 振型誤差||d?dh||和跨中截面結點C處( α=π/2 )位移誤差 ||dc?dch||并進行收斂階的統計，結果如圖4 和表1 所示。結果表明頻率和振型結點位移具有 2m階的超收斂性，而振型的收斂階僅為m+1階。

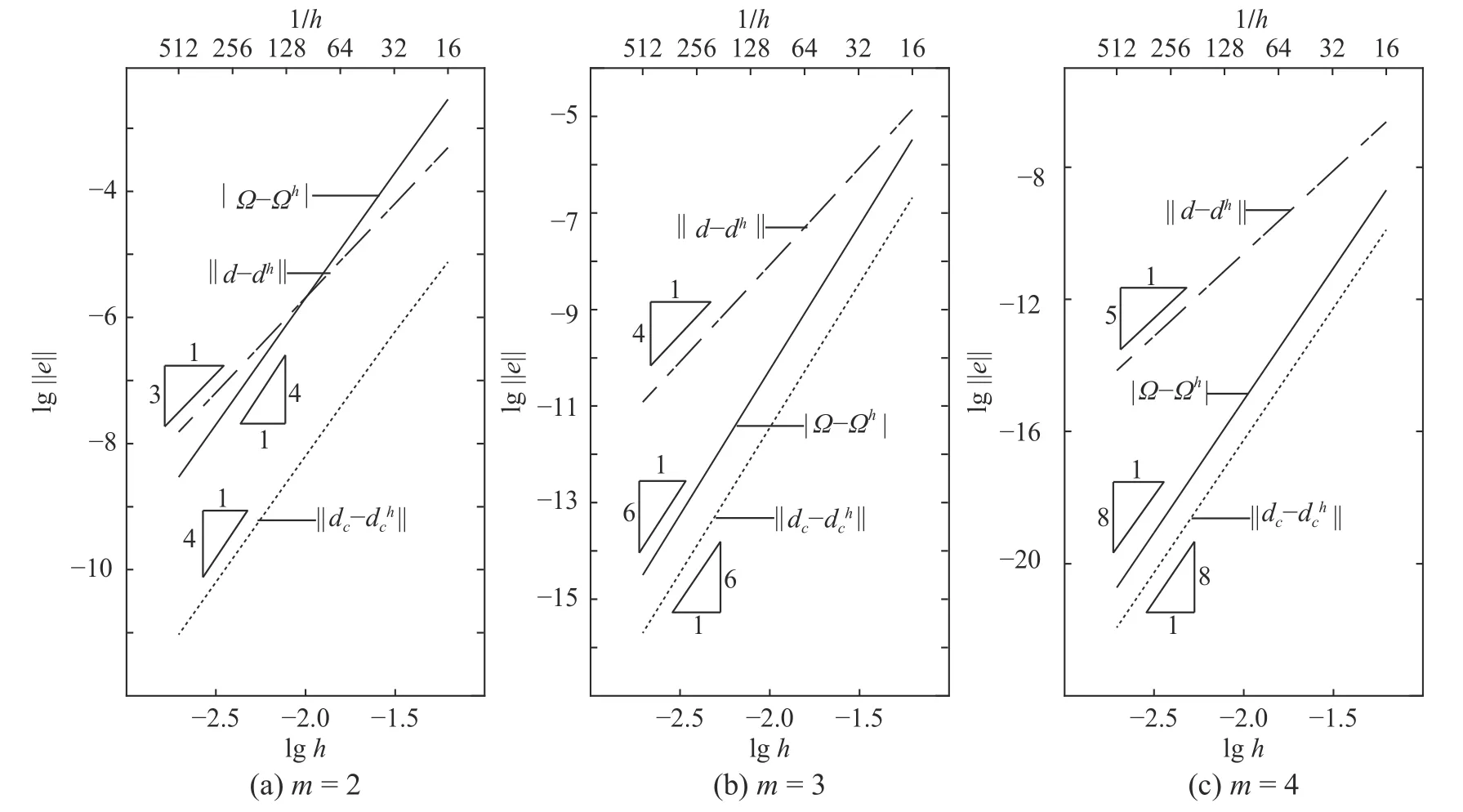
圖4 例1 第三階頻率、振型和結點位移的收斂階Fig.4 Rate of convergence of 3rd frequence, mode and its nodal displacement in Example 1

為考察p型超收斂算法的計算精度和修復效果，將曲梁均勻劃分為5 個單元，先用一次元(m=1) 進行有限元求解，再用二次元 (=2)進行超收斂修復。得到第三階頻率的有限元解為?h3=8.398 (相對誤差為300.5%)，超收斂解為??3=2.664(相對誤差為27.0%)。圖5 為第三階振型的有限元解、超收斂解和精確解的對比。可見，本文算法可以顯著提升頻率和振型的計算精度。

為考察p型超收斂算法的收斂階，對第三階頻率和振型，先用二次元 (m=2)進行有限元計算，再用三次元 (=3) 、四次元 (=4)和五次元(=5)進行超收斂修復并統計收斂階，計算結果如圖6 和表2 所示。易見，超收斂修復后，精度和收斂階與有限元解相比均有顯著提升。同時，由表2 可以看出，當從四次元 (=4)升至五次元(=5)時，頻率和振型的收斂階未隨之提升。理論分析和數值算例均表明，當>2m時，超收斂

解的收斂階與=2m時相同，不會隨的進一步提高而增加。

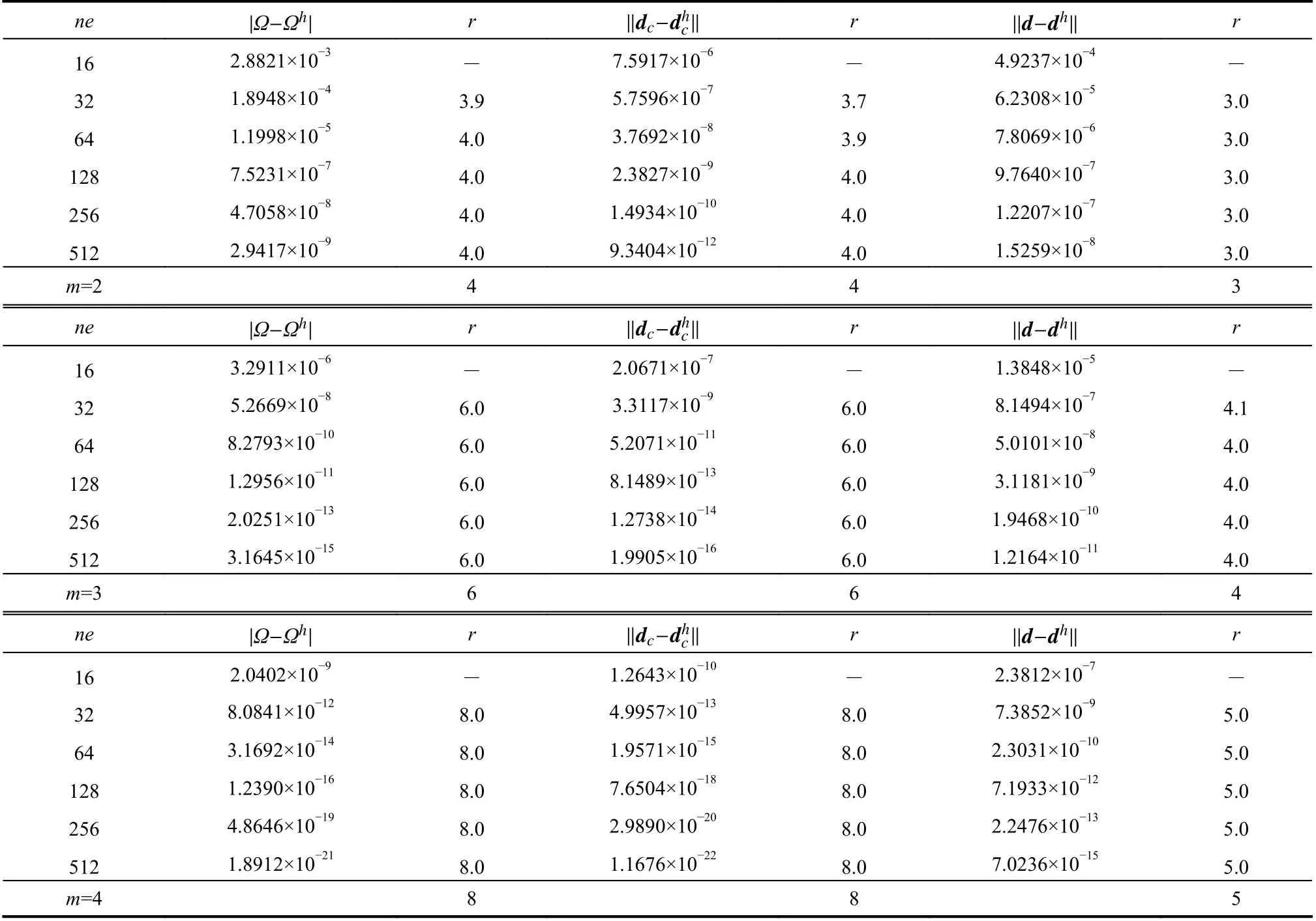
表1 例1 第三階頻率、振型和結點位移的收斂階Table 1 Rate of convergence of 3rd frequency, mode and its nodal displacement in Example 1

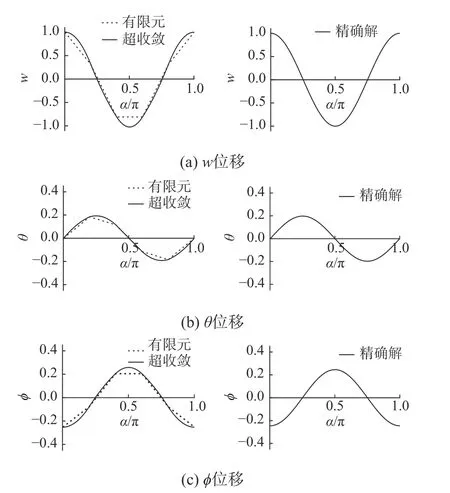
圖5 例1 第三階振型的有限元解與超收斂解比較Fig.5 Comparison of FE solution with recovered solution on 3rd mode in Example 1

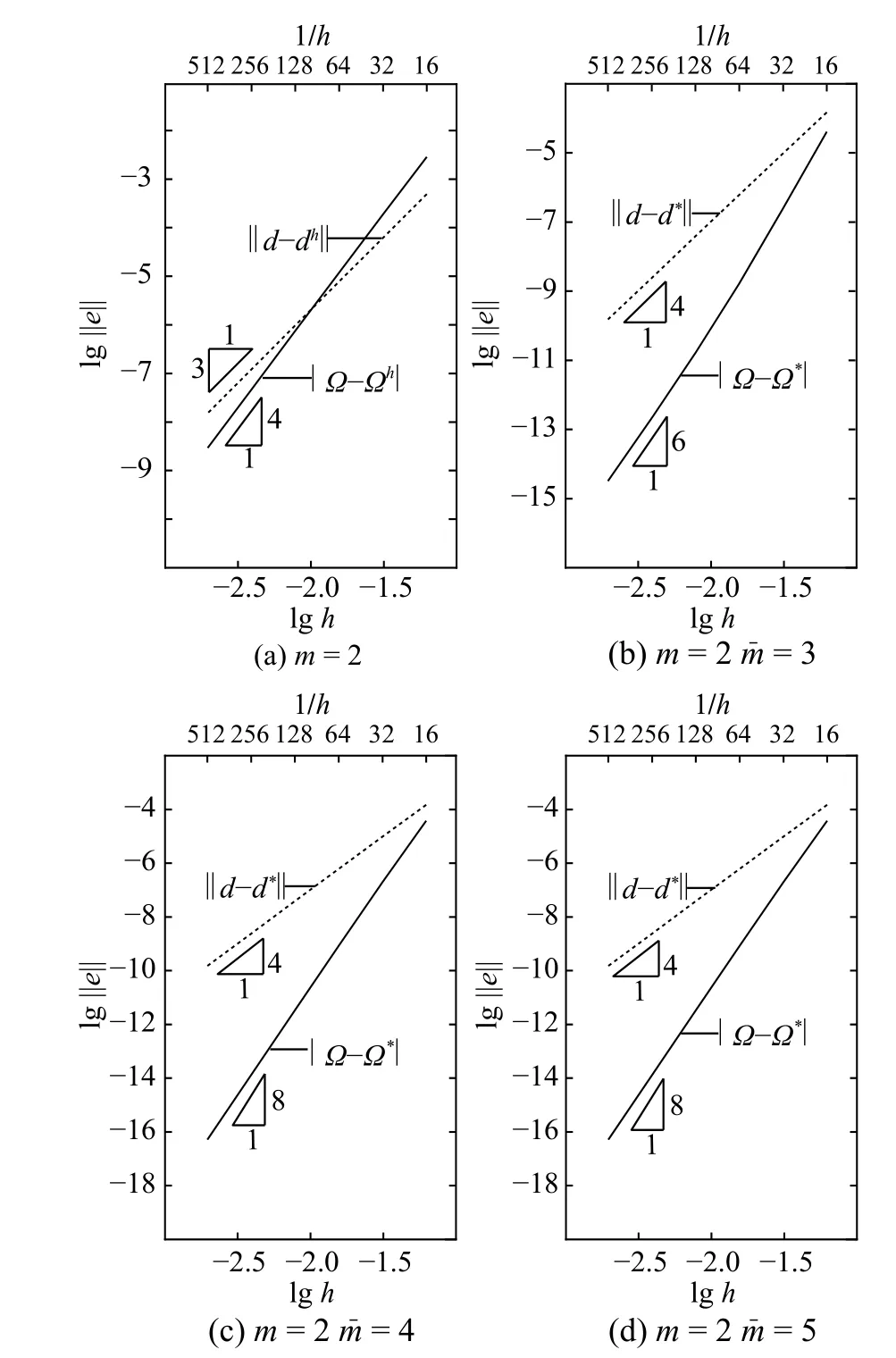
圖6 例1 第三階特征對有限元解與超收斂解收斂階Fig.6 Rate of convergence of FE solution and recovered solutions on 3rd eigenpair in Example 1

為對比本文算法與SPRD 法[11]的計算效果，對第三階頻率和振型的二次元解用SPRD 法進行超收斂修復，用相鄰四個結點(單元兩端結點外加離單元最近的兩個結點)上的位移解作三次多項式插值得單元上振型的超收斂解，將振型超收斂解代入Rayleigh 商得頻率超收斂解。頻率和振型的收斂階統計結果如表3 所示。可見，SPRD 法三次元修復解與本文算法三次元修復解的收斂階相同，只是同樣網格下SPRD 法的解答精度比本文算法的解答精度稍低些。

例2. 常截面圓弧曲梁2

本例仍取軸線為半個圓周的常截面圓弧曲梁，曲梁參數同例1，兩端支座形式改為面外簡支，如圖7 所示。

其振型可設為：

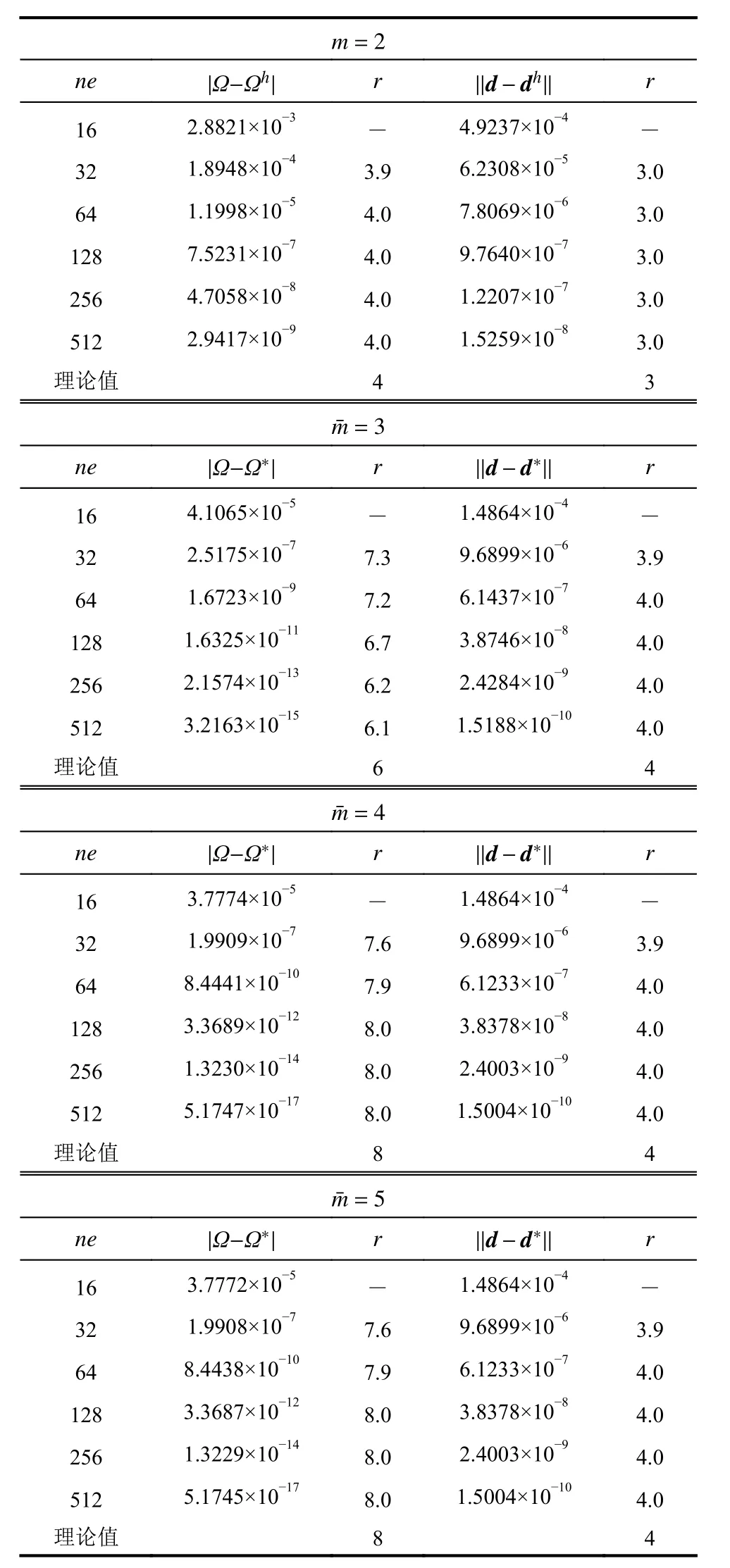
表2 例1 第三階特征對有限元解與超收斂解收斂階Table 2 Rate of convergence of FE solution and recovered solutions on 3rd eigenpair in Example 1

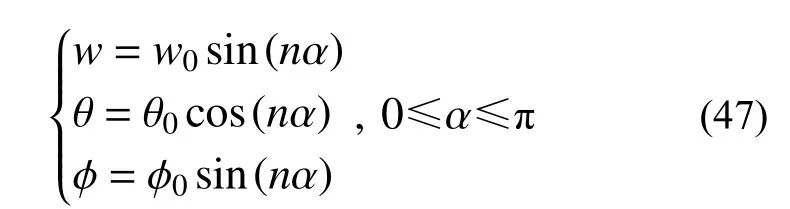
式中，n≥0且為整數。

將曲梁均勻劃分為32 個單元 (ne=32)，先用一次元 (m=1)進行有限元求解，再用二次元(=2)進行超收斂修復。前12 階頻率和振型的有限元解與超收斂解結果如表4 所示。易見，對一次元，雖然振型結點位移不具有超收斂性，本文方法仍能顯著提高解答(尤其是頻率)的精度。

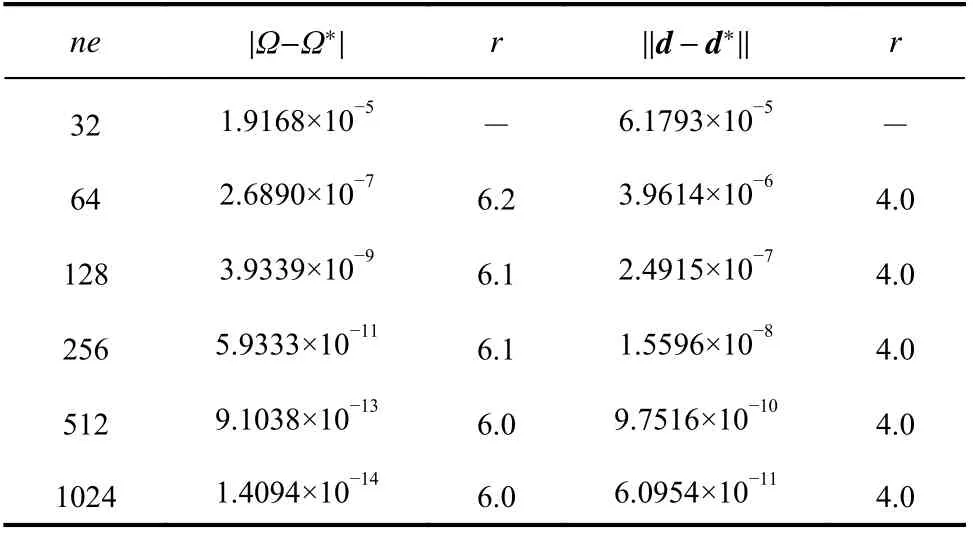
表3 例1 第三階特征對SPRD 法收斂階Table 3 Rate of convergence of recovered solutions on 3rd eigenpair in Example 1 with SPRD method

為考察本文算法對高階頻率和振型的計算效果，對該曲梁第26 階頻率和振型進行分析，此階對應n=14。按前述方法計算該階頻率和振型的精確解，精確解為：

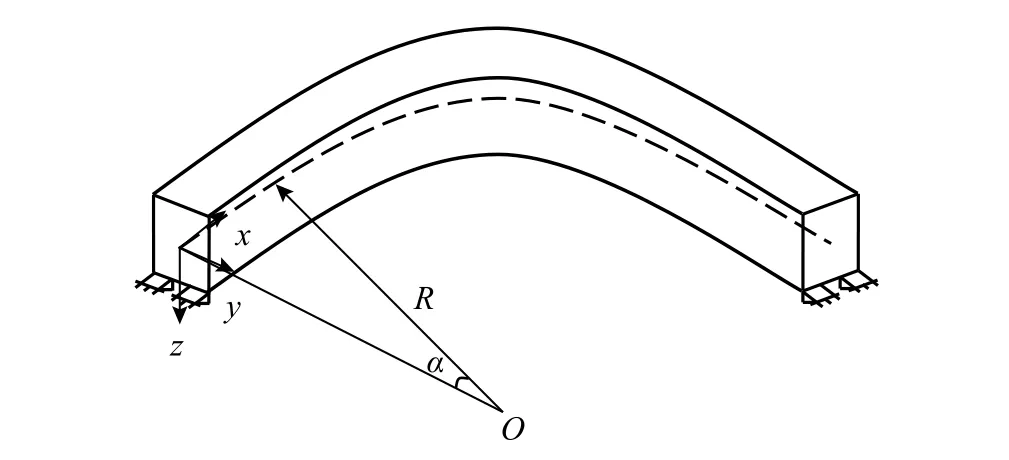
圖7 例2 常截面圓弧曲梁Fig.7 Uniform arch beam in Example 2

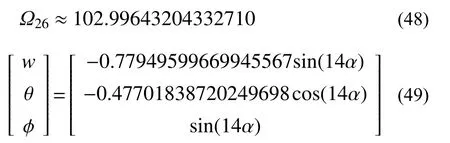
先用三次元 (m=3)進行有限元求解，再依次用四次元 (=4) 、五次元 (=5) 和六次元(=6)進行超收斂修復，結果如圖8 和表5 所示。結果表明p型超收斂算法對曲梁面外自由振動的高階頻率和振型仍有顯著的修復效果。

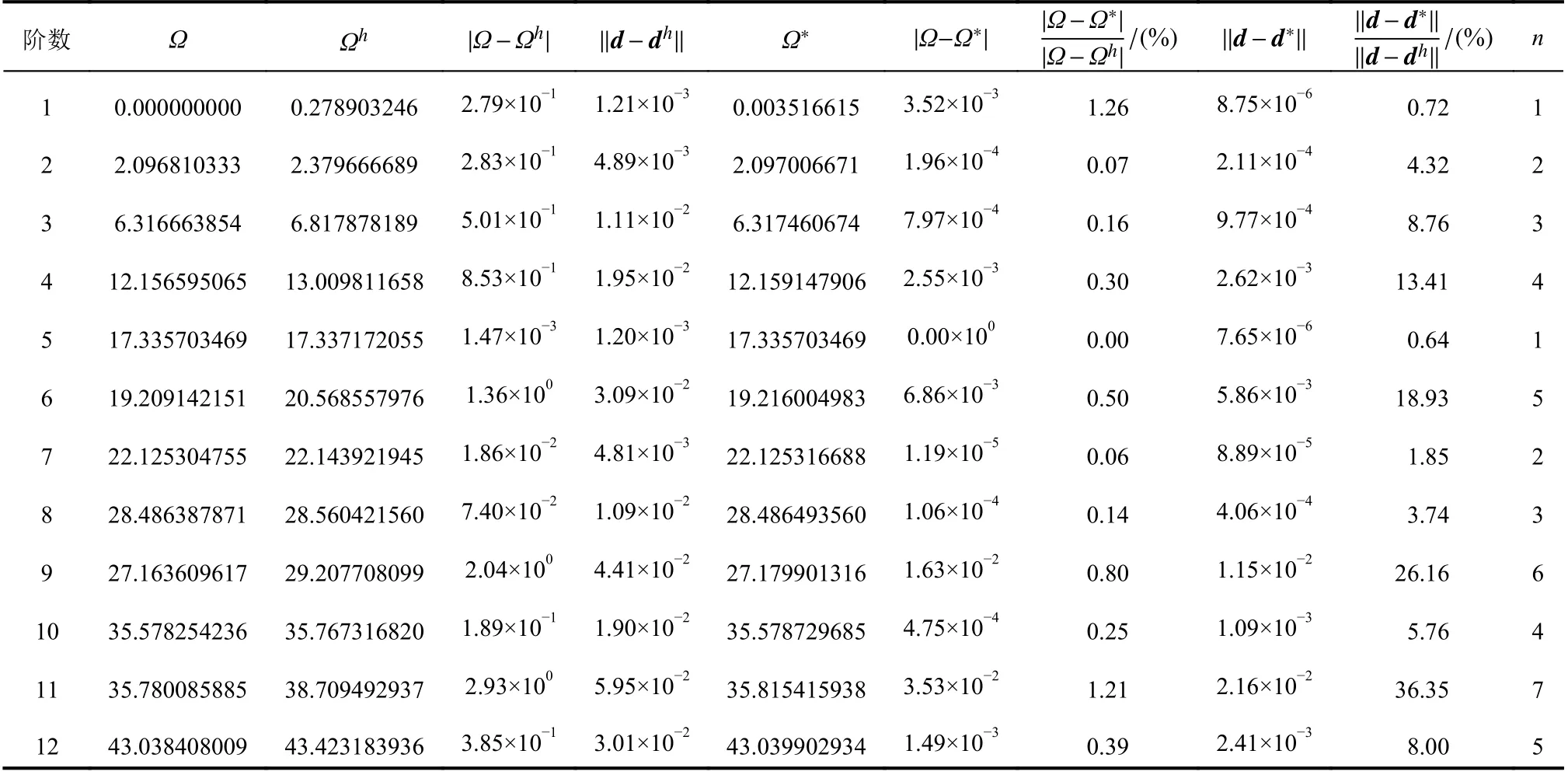
表4 例2 前12 階特征對有限元解與超收斂解誤差Table 4 Errors of FE solution and recovered solutions on first 12 eigenpairs in Example 2

例3. 一般軸線曲梁

文獻[27?28]研究了圖9 所示的拋物線、三角正弦線和橢圓線三類軸線曲梁的面外自由振動問題，三類曲梁軸線方程分別如下：

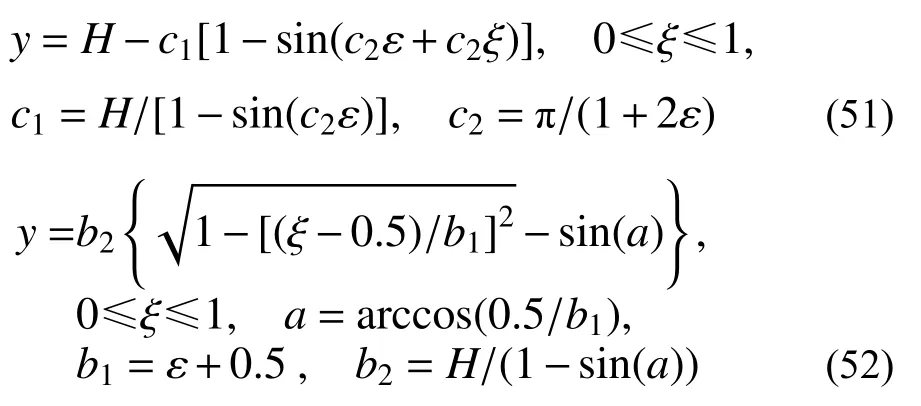
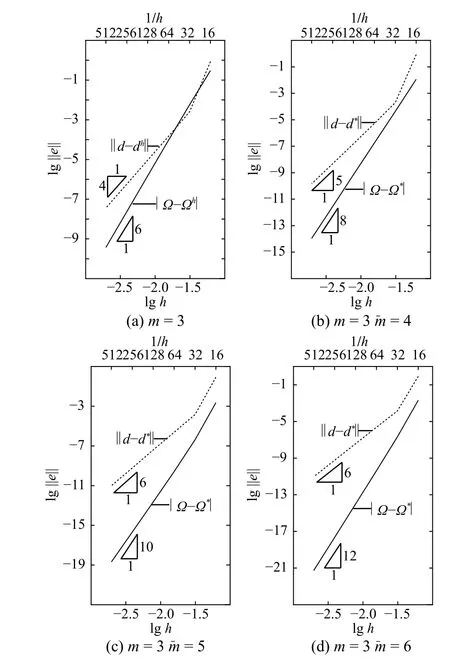
圖8 例2 第26 階特征對有限元解與超收斂解收斂階Fig.8 Rate of convergence of FE solution and recovered solutions on 26th eigenpair in Example 2

將三類軸線曲梁沿軸線水平投影方向均分為32 個單元 (ne=32) ，先采用一次元 (m=1)進行有限元計算，后采用二次元 (=2)進行超收斂修復和先采用二次元 (m=2)進行有限元計算，后采用三次元 (=3)進行超收斂修復，計算前3 階頻率如表6 所示。與文獻結果相比，頻率在一次元有限元計算后仍誤差較大，但采用二次元進行超收斂修復后，誤差顯著降低。而用二次元有限元計算后采用三次元進行超收斂修復，得到的解答與文獻結果已十分接近。表7 給出了上述網格下三類軸線曲梁前20 階振型有限元計算和超收斂計算的總耗時。可見，p型超收斂計算耗時很少，但解答精度提升非常顯著。在一次元有限元計算后用二次元進行超收斂修復，所得結果與直接用二次元進行有限元計算的精度已很相近，但計算總耗時不足后者的1/2，充分展現出p型超收斂算法提升精度的高效性。

綜合數值算例，本文超收斂解的收斂規律如表8 所示。

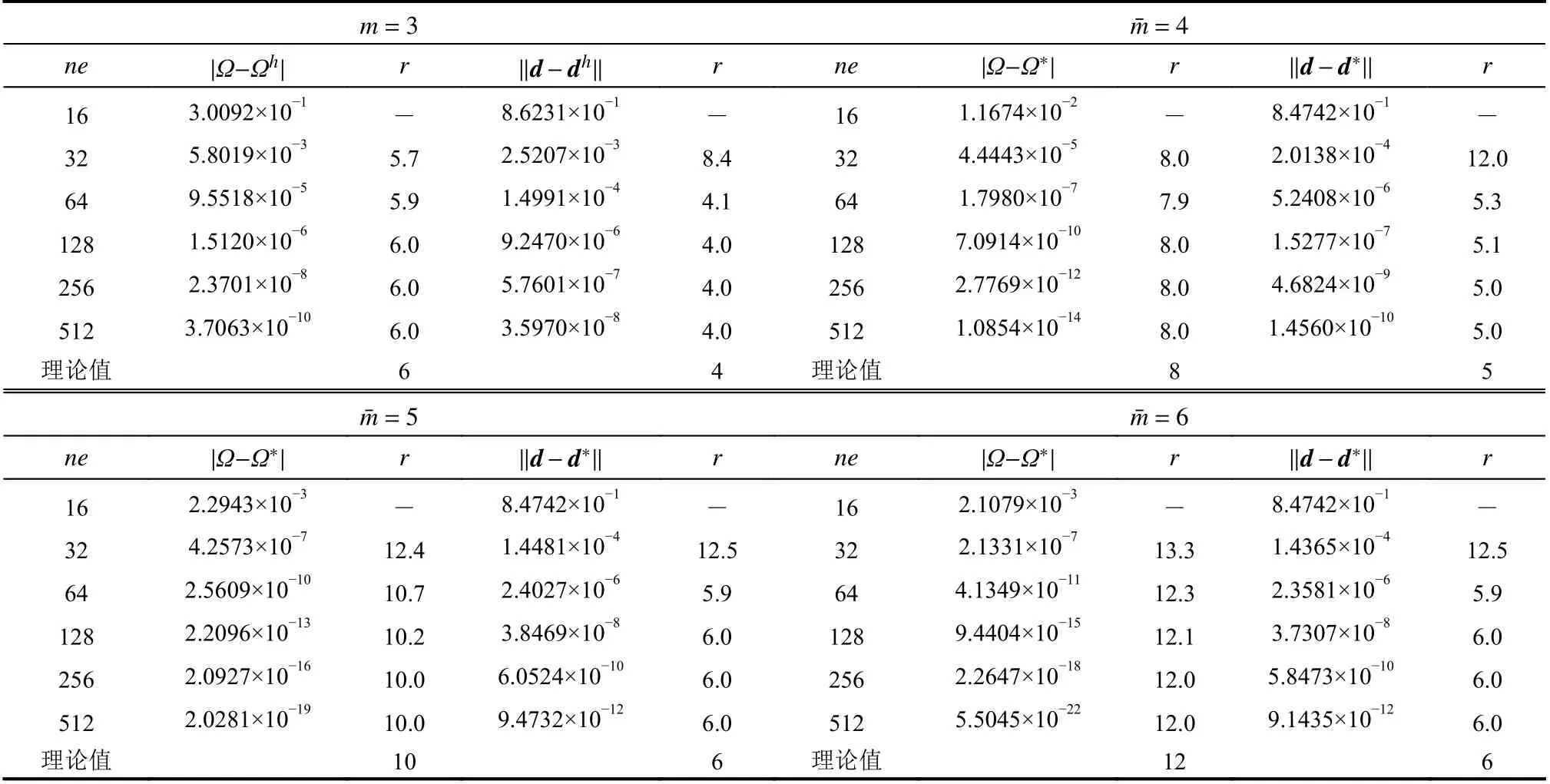
表5 例2 第26 階特征對有限元解與超收斂解收斂階Table 5 Rate of convergence of FE solution and recovered solutions on 26th eigenpair in Example 2

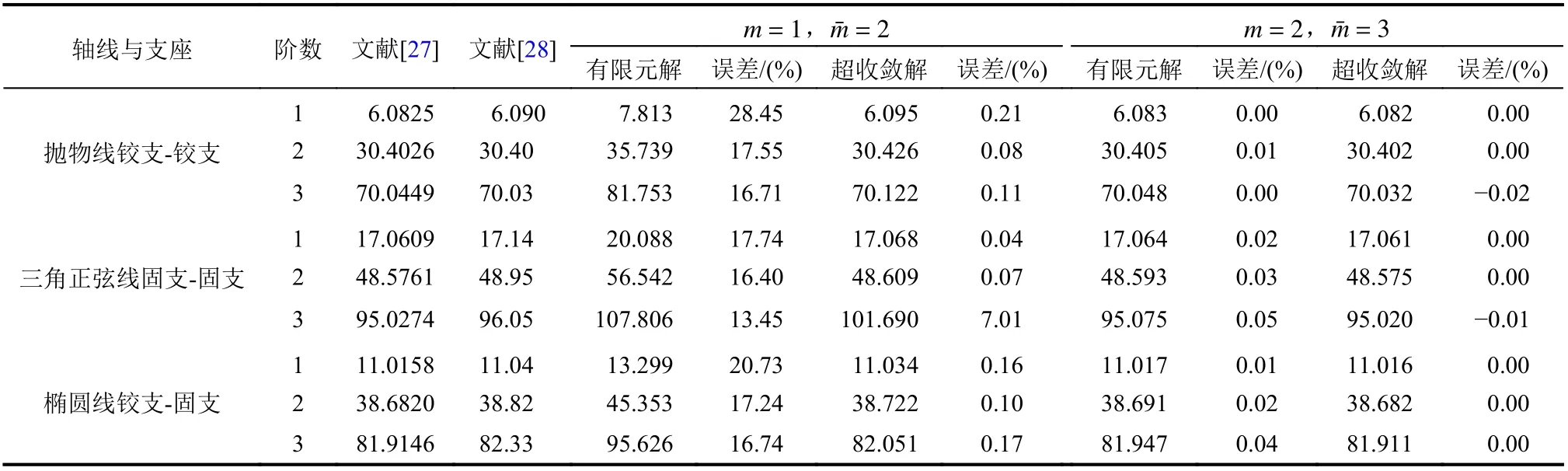
表6 例3 三類軸線曲梁的無量綱頻率Table 6 Dimensionless frequencies for three curved beams of Example 3

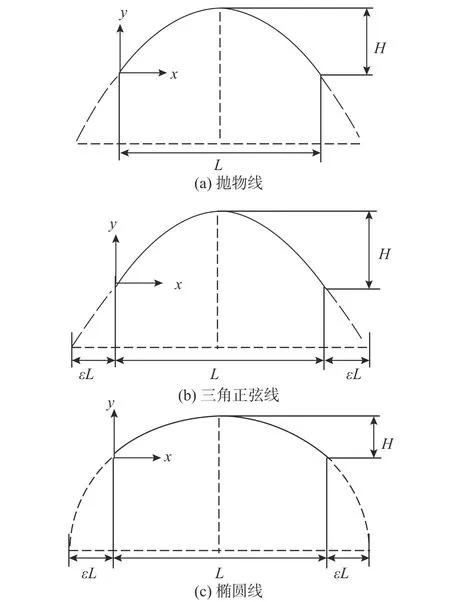
圖9 三類軸線曲梁Fig.9 Three types of curved beams

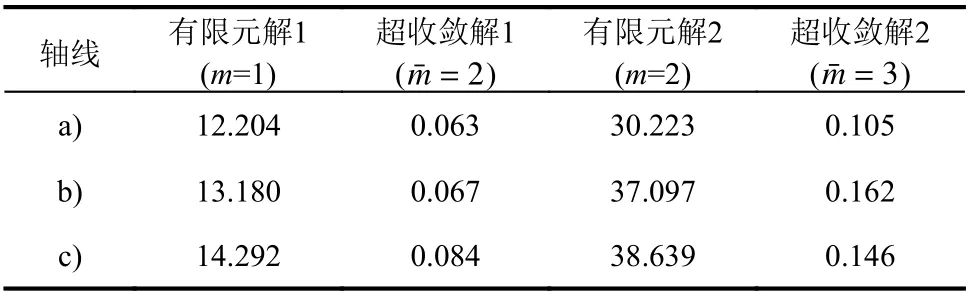
表7 例3 前20 階振型計算總耗時 /sTable 7 Total computation time for first 20 modes of Example 3

表8 超收斂解的收斂階Table 8 Convergence order of recovered solutions

5 結論

本文的p型超收斂算法在有限元解的基礎上，充分利用頻率和振型結點位移所具有的超收斂特性，通過逐單元求解振型近似滿足的線性邊值問題獲得頻率和振型的更高精度解，方法思路巧妙，穩定高效，能顯著提高解答精度和收斂階，可進一步推廣應用到包括薄壁結構等空間結構自由振動的分析中。